基于改进FMECA的动车组牵引传动系统危害度分析
2021-07-26刘思文李永华
刘思文,李永华,宫 琦
(大连交通大学机车车辆工程学院,辽宁 大连 116028)
1 引言
转向架是动车组的重要承载部件,其运行平稳性、可靠性直接影响列车的运行安全。其中牵引传动系统作为转向架传递驱动力的重要部件,长期处于恶劣的工作环境下,承受来自环境和轨道不平顺产生的各种冲击、振动等附加动载荷影响,故障发生频率较高,给列车运行安全带来严重威胁。因此,统计系统故障模式、分析故障原因,采用合理的故障分析方法进行危害度分析,对其维修方案的制订和可靠性的提高具有重要的实际意义。
目前,针对牵引传动系统故障分析的FMECA方法主要是通过综合分析整个系统各组成部分的故障模式、故障原因和故障影响,确定各故障模式发生度(O)、严酷度(S)、可探度(D)的评估结果,计算三者乘积得到风险优先系数(RPN),再根据RPN值的大小进行危害度排序,确定系统薄弱环节。但是传统FMECA方法在应用时依赖于大量故障数据,O、S、D等级由专家经验给定,主观性过强,难以得到准确的分析结果;此外,在计算不同故障模式RPN值时,未考虑三者相对重要度,结果往往不够客观;不同评估结果的组合,RPN值可能相同,与实际故障模式潜在风险不同相违背。为解决上述问题,国内外学者提出了各种改进FMECA方法,并取得了大量的研究成果。文献[1-3]将FMEA方法和模糊层次分析法相结合,构造相对重要矩阵确定评估因素的权重向量;文献[4]提出工艺优化优先数分析方法并结合模糊综合评判模型对齿轮制造工艺参数优先等级排序,克服传统RPN分析方法权重分配不足的问题;文献[5]将模糊理论引入PC-FMECA方法中,并以数控磨床液压系统为例进行分析,得到更为理的维修策略;文献[6]在模糊理论与灰色关联分析基础上,考虑失效模式与失效原因间的相关关系应用DEMATEL方法,得到更精确的失效模式风险水平;文献[7]在模糊环境下结合多决策准则和层次分析法的混合权重计算方法,实现模糊因素的量化,避免主观性的影响。上述文献在FMECA分析中引入模糊理论将模糊指标定量化,一定程度上解决了传统方法中的定量分析不确定性,但当危害因素集中时,仅从权重分配角度进行处理很难实现危害度的完全排序。而且将专家评估结果平整化,忽略了不同专家的经验差异。对此文献[8]在过程失效模式与分析(PFMEA)方法中应用模糊层次分析法,并结合专家判断矩阵合理分配专家权重。文献[9]应用直觉乘法数和直觉乘法偏好矩阵修正专家偏好信息,并利用改进优劣解距离算法(TOPSIS)对故障模式进行风险排序,得到更准确的评估结果。但以上方法基于判断矩阵求解专家权重仍存在一定主观性,忽略了专家间评估结果的融合。
因此,从提高专家评估结果融合精度的角度出发,充分利用D-S证据理论在证据合成上的优势,提出了一种基于模糊综合评判与D-S证据理论结合的分析方法,计算各故障模式的危害度。该方法不仅克服了传统FMECA方法评估过程的主观性,同时提高了专家评估结果的融合精度,得到更符合实际的评估结果,为制订合理、有针对性的维修方案提供了更加准确的数据支撑。
2 基于模糊综合评判和D-S 证据理论的改进FMECA方法
2.1 模糊综合评判模型
模糊综合评判是一种基于模糊理论的综合评价方法,该方法利用隶属度理论和模糊线性变换原理将复杂系统评估由定性评价转化为定量评估,并以其结果清晰,系统性强等优点,广泛应用于各种非确定性问题的研究[10]。其基本思想是将评估结果模糊化,结合权重变量实现多因素综合评判。模糊综合评判步骤如下:

图1 模糊综合评判计算步骤Fig.1 Calculation Steps of Fuzzy Comprehensive Evaluation
2.1.1 确定因素集和评价集
因素集是对评价对象产生影响的各种因素组成的集合,用U表示。设U={u1,u2,…un} 为n种因素或指标,ui即为第i个因素。评价集是指专家对评价对象对因素集影响的评价等级的集合,用V表示。设V={v1,v2,…vm} 为m种不同评判,vj即为第j个评价等级。
2.1.2 确定隶属度
因素集对评估对象的影响程度不同,需要考虑各因素权重即确定其隶属度,以刻画影响因素的因素集对评价集的隶属程度。
2.1.3 构造模糊评价矩阵
根据因素集U到评价集V之间的模糊映射求得隶属度计算结果,确定其模糊关系∈(U×V),即:

2.1.4 基于权重向量的模糊综合评判
权重即比例系数,是不同模糊变量相对重要度的体现。在综合评判前结合因素集各因素对评价集指标的相对重要度,求得模糊因素权重向量W={w1,w2,…wn},最后由综合评判模型计算得:

2.2 矩阵合成的D-S证据理论
D-S证据理论是一种不确定性推理方法,该方法不需要关于集合或区间的单个因素的概率假设,可直接利用多个不确定来源的信息和描述,将信息来源不确定性转化为集合不确定性,有效解决专家主观性问题。但部分学者指出直接应用Dempster规则不仅存在焦元爆炸的问题,还伴有证据冲突的现象。主要表现为专家数增多,计算时间呈指数增加;证据间冲突较大时,冲突系数近似为1,计算结果不理想。因此,不少学者提出了各种改进D-S合成算法[11-13]。对比各种改进D-S合成算法后,选择基于矩阵分析的D-S合成算法[14]。
假设有n位专家同时评估某一故障模式,可能的评估结果有m种。评估结果构造成相应的基本概率分配函数,则专家评估结果的置信度分配用矩阵M表示:
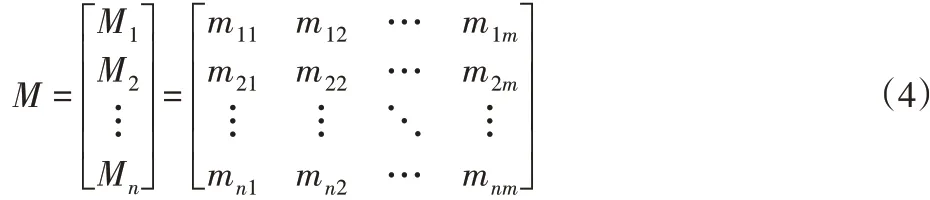
式中:mij—第i位专家给出的目标为第j种类型的置信度。且矩阵的每行元素满足归一化条件。将矩阵某一行的转置与另一行相乘得M1即:
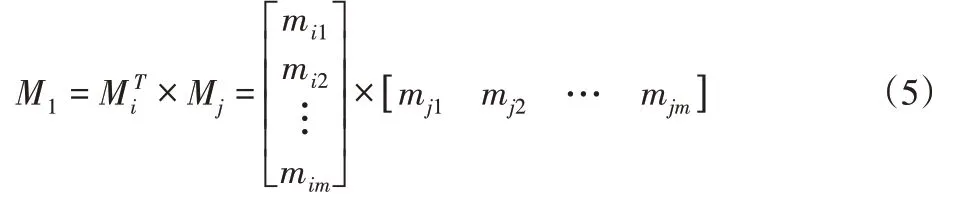
主对角线元素为2位专家评估结果的融合,非主对角线元素之和构成专家融合结果的冲突因子。
2.3 改进FMECA方法基本理论
综合上述模糊综合评判和D-S证据理论在处理不确定问题上的优势,提出基于模糊综合评判和D-S证据理论的改进FMECA方法,在模糊隶属度矩阵基础上,应用矩阵合成的D-S证据理论算法融合专家评估结果,最后结合权重向量确定各故障模式危害度。
设系统故障模式为Fi(i=1,2,…,n),选取故障模式对系统影响的三个常用指标(O、S、D)进行评估。改进FMECA方法分析流程,如图2所示。
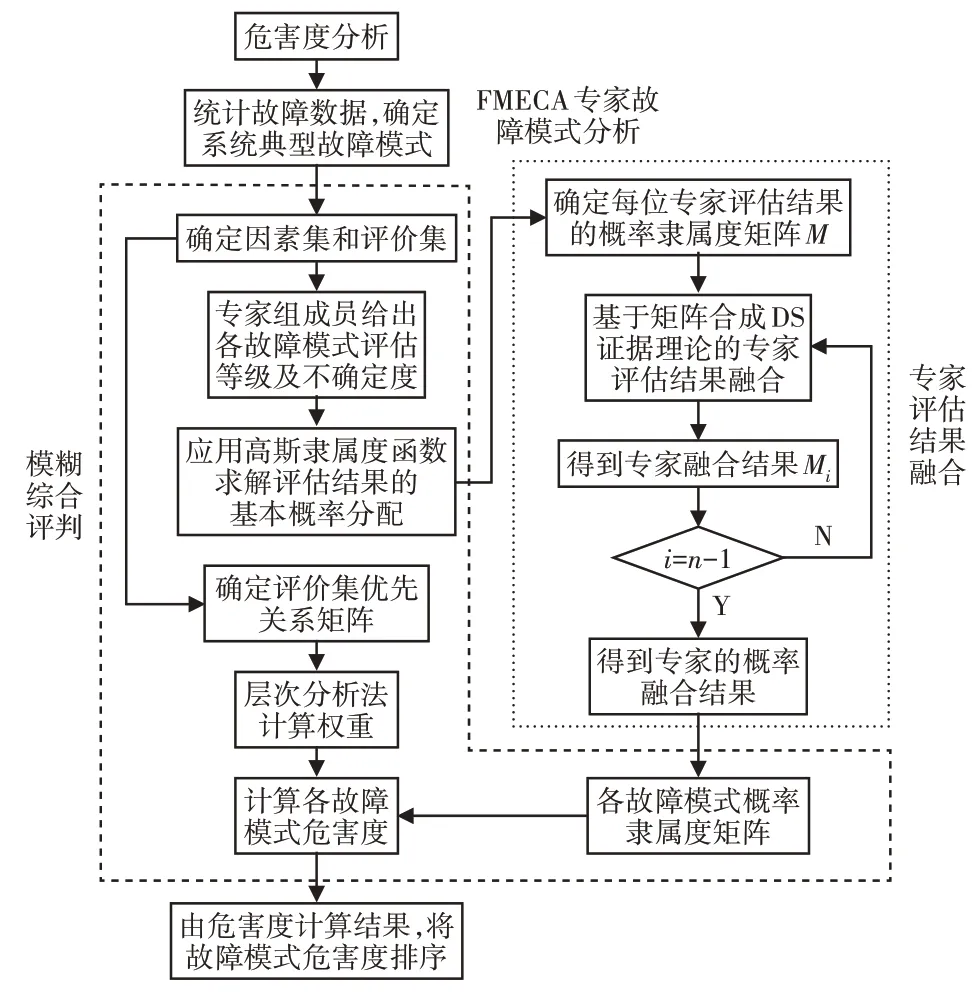
图2 改进FMECA方法分析流程Fig.2 Improved FMECA Analysis Process
(1)结合统计故障数据,选取部分故障模式进行分析,应用FMECA方法分析系统故障模式及发生原因;
(2)确定模糊综合评判因素集U即故障模式对系统影响的三个常用评价指标:
U={发生度,严酷度,可探度}
给定因素集对应评价集V,并定义其不同等级对应的量化值;
(3)各专家故障评估结果的基本概率分配;
在(1)和(2)的基础上,由专家组成员给定故障模式的风险等级和评估不确定度,选取高斯隶属度函数反应其分布特性,并将评估结果量化为高斯隶属度函数中心和宽度指标:
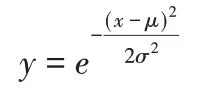
基于高斯隶属度函数分布规律计算专家评估结果的基本概率分配指标,并将结果归一化处理;
(4)由上述步骤专家组对某一因素集评估结果确定基本概率分配矩阵,应用基于矩阵合成的D-S融合算法进行计算,将最终融合矩阵主对角线元素及所有融合矩阵非主对角线求和,结果即冲突程度K代入下式:
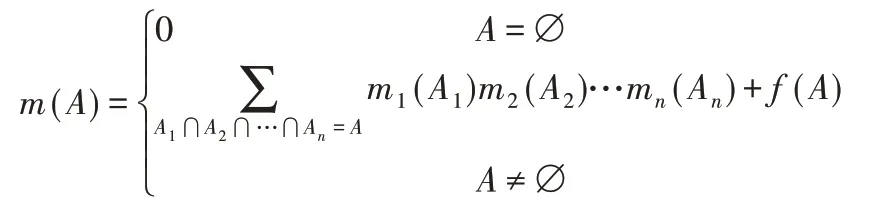
式中:f(A)—所有专家在证据冲突下对评估因素所属等级的概率分配,其表达式如下:
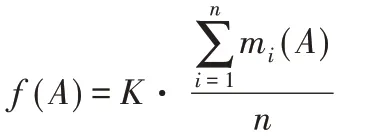
因此,各故障模式隶属不同等级的隶属度融合计算值为:
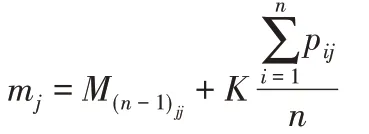
(5)确定评价集权重;
利用三标度层次分析法[15-17]建立发生度、严酷度、可探度三者之间的比较矩阵F(优先判断矩阵):
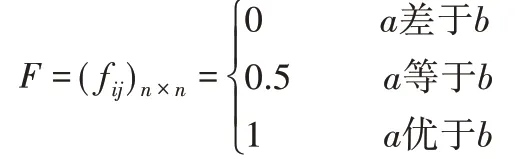
首先将模糊评判矩阵各行求和,并利用下式将矩阵F改造为模糊一致性评判矩阵G=(qij)n×n。
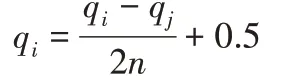
其次,应用行和归一化法,将矩阵G每行指标(不含自身)和不含对角线指标元素分别求和得:

则权重向量为w=(w1,w2,…,wn);
(6)系统故障模式危害度的确定;
基于(4)得到故障模式k的模糊隶属度矩阵Rk,并利用下式计算该故障模式模糊综合评判模型Bk,最后加权计算该故障模式的危害度C;
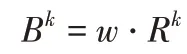
(7)确定故障模式危害度排序;
将上述求得危害度值进行排序,C值越大,相应故障模式引发安全性事故的风险越大,故有必要采取合理的方案降低故障发生风险。
3 工程案例分析
3.1 牵引传动系统FMECA分析
以某动车组牵引传动系统故障为例进行分析。牵引传动系统作为转向架驱动力的主要来源,主要包括牵引电机、联轴器和齿轮箱等。牵引电机将接触网传来的电能转化为机械能,输出电磁转矩;联轴器将牵引电机输出的扭矩传递给齿轮箱;齿轮箱的作用是将联轴器传递的扭矩作用在齿轮轴上,齿轮轴转动带动小齿轮,并通过齿轮啮合,将牵引电机输出的扭矩传递给车轮,驱动车轮前进,实现列车高速运行[18]。基于牵引传动系统工作原理及已有故障数据,选取部分故障模式进行研究,评估其O、S、D等级,计算RPN值,分析结果,如表1所示。由FMECA表可清晰的得到系统故障模式、影响及原因,将RPN值排序,确定轮齿折断和箱体裂纹、断裂危害度较高。但牵引传动系统结构复杂,各故障模式间的相互影响,故障模式危害度较为集中,部分故障模式RPN值完全相同,与实际情况不符。
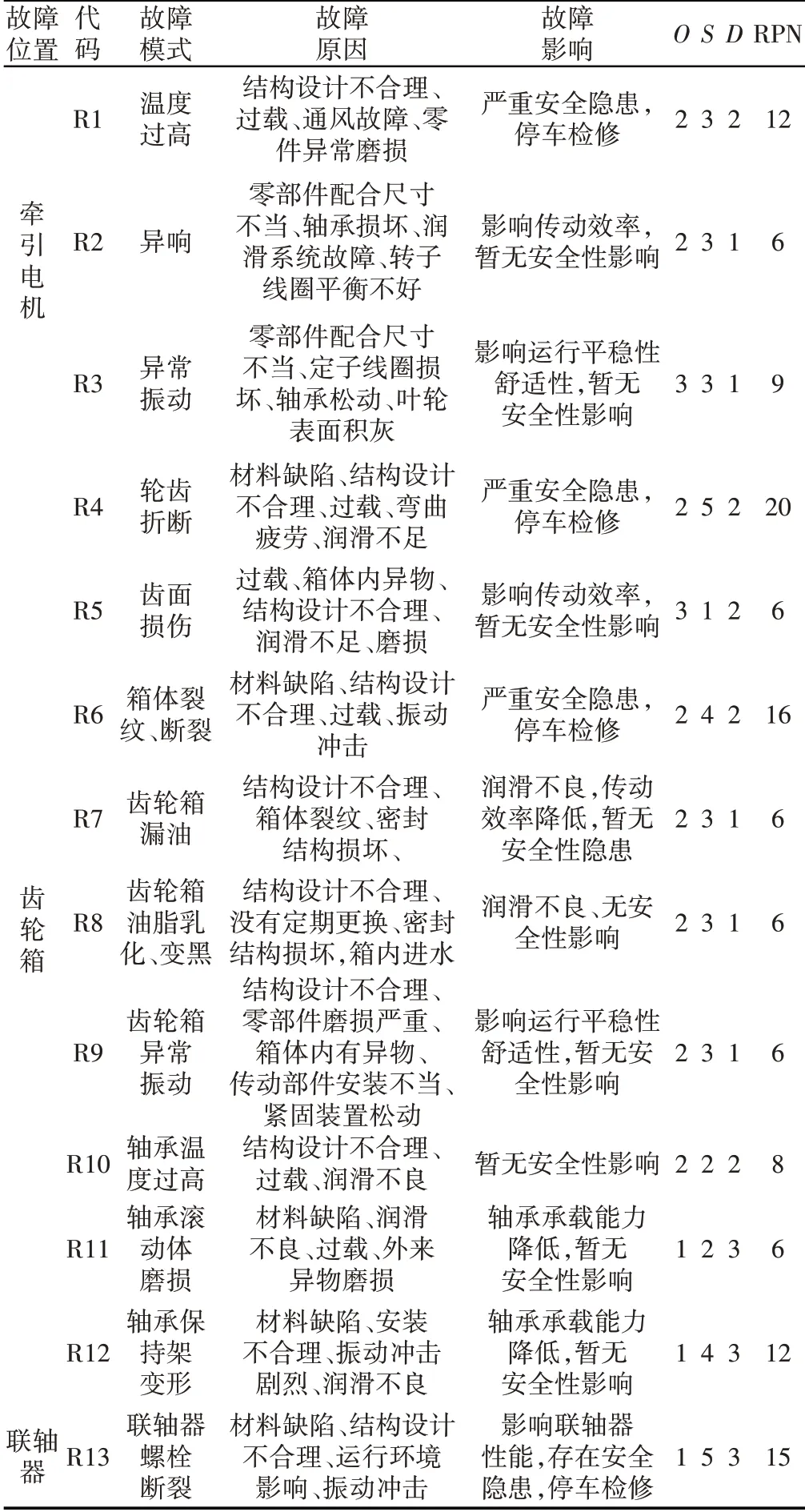
表1 牵引传动系统FMECA表Tab.1 Traction Drive System FMECA Table
3.2 改进FMECA评估过程
为提高FMECA方法定量分析的准确性,应用基于模糊综合评判和D-S证据理论相结合的改进FMECA方法对上述13种故障模式进行分析,以得到更符合实际的危害度排序结果。具体步骤如下:
选定影响系统危害性分析的三种常见因素:O、S、D为模糊综合评判因素集。定义评价集V={1,2,3,4,5},模糊评判因素集和评价集对应关系,如表2所示。

表2 因素评价等级表Tab.2 Factor Evaluation Grade Table
选取高斯隶属度函数刻画专家评估结果的基本概率分布,不同等级对应的隶属度函数如下:


式中:μ—隶属度函数中心,即专家所给评估等级对应的量化值。定义不同等级对应隶属度中心分别为0、0.25、0.5、0.75、1。
σ—函数宽度,即专家评估等级不确定度的量化值,该值越大,表明专家对评估结果的不确定度越高。
由专家小组对表1所示13种故障模式进行评估,以严酷度为例给出不同故障模式所处的评价等级及不确定度量化结果,如表3所示。
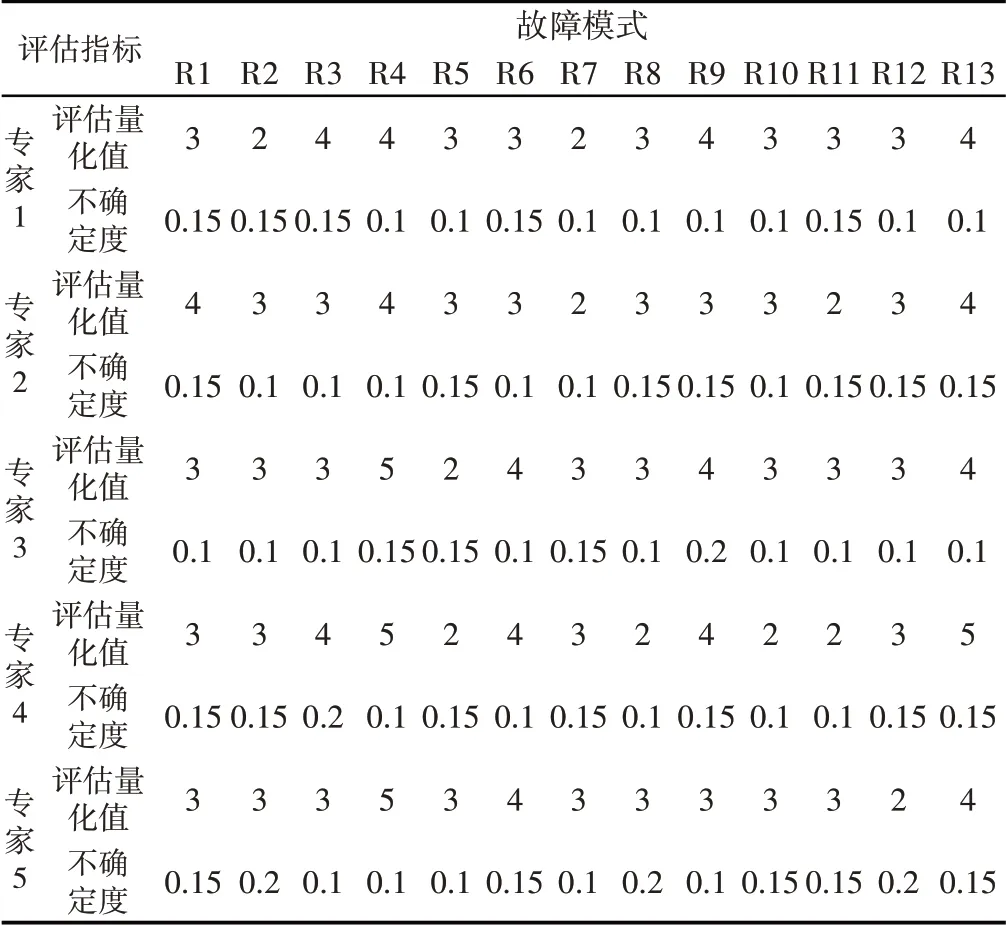
表3 专家严酷度评估结果Tab.3 Expert Severity Assessment Results
基于表3专家评价结果和高斯隶属度函数式(6)~式(10)进行计算,将计算结果归一化处理,可求出5位专家评估结果的基本概率分配。
确定每位专家严酷度评估结果的基本概率分配矩阵,利用矩阵合成的D-S证据理论融合5专家的评估结果,可得严酷度融合后的概率分配结果,如表4所示。
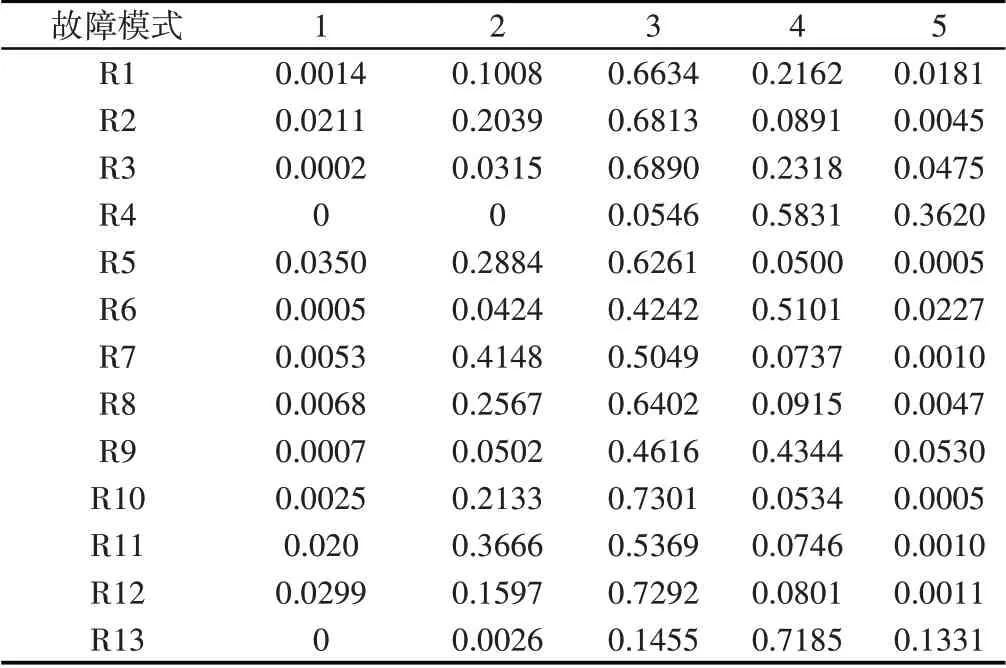
表4 严酷度融合后的概率分配Tab.4 Probability Distribution of Severity Fusion
同理,可得到发生度和可探度融合后的概率分配结果,从而确定各故障模式的隶属度矩阵Rk:
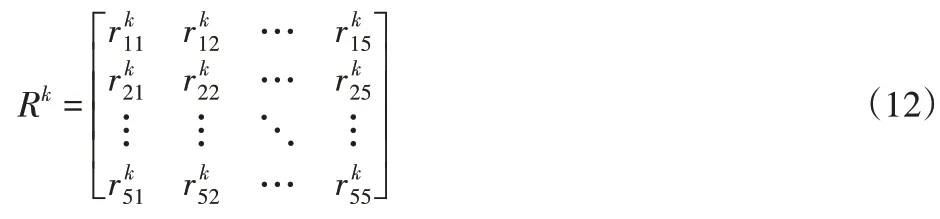
依据表2对牵引传动系统故障模式的3个影响因素的评价等级进行分析,牵引传动系统发生度、严酷度和可探度权重关系为:严酷度>发生度>可探度。由三标度层次分析法得三者优先关系矩阵,如表5所示。

表5 优先关系矩阵Tab.5 Precedence Relation Matrix
计算出模糊集权重为w=(0.3333,0.5000,0.1667)。以轮齿折断为例,确定该故障模式的隶属度矩阵为:

由上述求得的权重集w,根据模糊综合评判模型进行评判,评判结果如下:
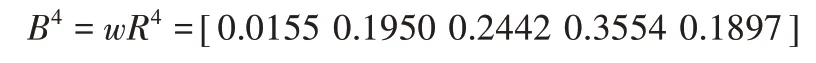
B表示模糊评价集,应用公式C4=B4VTC,确定该故障模式的综合危害度评价结果为C4=3.5081。同理,可分别计算出其他故障模式的危害度。


将上述求得危害度排序得:轮齿折断>联轴器螺栓断裂>箱体裂纹、断裂>齿轮箱异常振动>电机异常振动>电机温度过高>轴承保持架变形>齿面损伤>轴承温度过高>齿轮箱油脂乳化、变黑>齿轮箱漏油>轴承滚动体磨损>电机异响。其中轮齿折断、联轴器螺栓断裂及箱体裂纹、断裂危害度最高,应作为牵引传动系统中结构改进和维修决策的重点。
3.3 评估结果分析
基于模糊综合评判和D-S证据理论的改进FMECA 方法不仅考虑了牵引传统系统故障模式发生度、危害度和可探度三者间的权重差异,同时利用DS证据理论在证据融合上的优势,实现了专家结果的有效融合,提高了评估结果的准确性。
结合给定专家评估不确定度的方法,不确定值越大,专家评估意见的不确信度越高,能够更好反应出真实情况,提高评估意见的可信度。以故障模式R11可探度为例进行讨论,五位专家给出的评估等级分别为3、3、2、4、3,由高斯隶属度函数可求得基本概率分配结果,如表6所示。由表可见,专家评估结果冲突较大,采用传统合成法则与采用的合成法则分别将五位专家评估结果进行融合,对比结果,如表7所示。
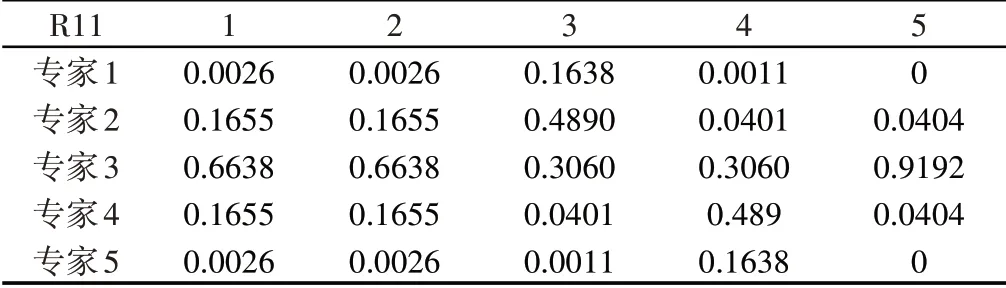
表6 R11专家评估结果基本概率分配Tab.6 R11 Basic Probability Distribution of Experts

表7 合成结果对比Tab.7 Comparison of Fusion Results
由表7可得,原始D-S证据合成算法融合后评估等级为3级的概率近似为1,而与实际专家评估结果分散相违背,因此传统方法无法准确的反应不同专家主观性的差异。而算法得到的基本概率分配结果对专家评估结果的量化效果更好、准确度更高,其结果更符合实际情况。能够为后续结构改进和维修保障方案的制订提供参考。
4 结论
采用模糊FMECA 和矩阵合成D-S证据理论相结合的方法对高速列车牵引传动系统故障模式进行分析,结论如下:
(1)在传统FMECA的RPN分析方法基础上,提出基于模糊综合评判与D-S证据理论相结合的改进FMECA方法的研究,建立高速列车牵引传动系统模糊综合评判模型,得到各故障模式危害度排序结果。为结构设计改进和维修决策奠定基础。
(2)该方法通过对故障模式和专家评估结果等不确定信息进行量化,进而确定系统薄弱环节,有效解决了高速列车牵引传动系统故障模式危害度集中和危害度排序困难的问题,将专家评估结果融合引入FMECA方法中,所得分析结果切合实际。
(3)对高速列车牵引传动系统的故障模式危害度进行排序,并提出相应的结构改进重点和维修决策方案,为牵引传统系统可靠性提高提供了参考和指导。该方法也同样适用于其他系统故障模式危害度的计算和排序,具有一定的参考价值。
