防城港湾潮余流及潮汐不对称特征

2021-07-25李谊纯董德信王一兵

广东海洋大学学报 2021年4期

李谊纯，董德信，王一兵

（1.广西民族大学海洋与生物技术学院，广西南宁 530008；2.北部湾大学建筑工程学院，广西钦州 535011；3.广西科学院广西近海海洋环境科学重点实验室，广西南宁 530007）

防城港湾面积约160 km2，大部分海域水较浅，潮间带宽阔。湾口门向南敞开，东邻企沙半岛，西为白龙半岛，中部被NE—SW 走向的渔澫半岛分隔成东湾和西湾。近20 a 来，随着泛北部湾区域经济发展及泛珠三角经济合作，防城港湾及其周边区域逐渐成为经济开发热点区域，岸线资源和海域空间资源被大规模利用，水动力条件被人为改变，海洋环境污染问题日益凸显。防城港及其邻近海域潮汐以正规全日潮为主，最大潮差约5.63 m；潮流属非正规全日潮流。陈波等[1-3]根据实测水文数据得出正常天气下，防城港海域潮流流速小于0.5m/s，余流小于0.2 m/s，余流场具有明显的季节性变化，在台风期间余流可超出正常值3 倍。施华斌等[4]利用二维浅水模型模拟分析北部湾潮流系统，认为防城港西湾内余流较弱，东湾内余流较强，并据此认为东湾水体交换能力较强。关于余流的组成，陈宜展等[5]、陈波等[6]基于实测资料得出余流方向与风向基本一致，表现出风海流特征；潮致余流和密度流对余流构成也有不可忽视的贡献。孙洪亮等[7]的研究亦得出类似结论，并认为大—小潮变化及风速风向变化均可引起余流变化。诸多研究均指出风生余流、潮致余流是防城港海域余流的重要组成部分。其它研究，诸如李树华等[8-9]则认为防城港湾内的潮致余流流速较小，一般为0.01～ 0.03 m/s。

防城港湾潮汐动力过程研究取得一定成果，但以往的研究多基于Eular 余流分析。Longuet-Higgins[10]指出，Stokes 输运是水体输运的重要机制。在近岸浅水区域，由于潮汐发生变形，Eular 余流不一定能够反映真实的水体输运速度和方向。即使在无淡水注入的河口海湾，由于潮汐变形，Eular 余流也常指向下游。在近岸区域，水体的余流可表示为Lagrange 余流=Eular 余流+Stokes 余流[11]，Lagrange 余流反映了水体及水中物质的真实输运。此外，潮汐和潮流不对称对近岸物质输运具有重要意义和指向作用，潮汐变形对水体（物质）输运存在较大的潜在影响。防城港湾水浅滩阔，地形地貌较为独特，对其潮汐和潮流不对称特征及其产生原因的研究未见报道。鉴于此，笔者建立防城港湾潮汐数学模型，对防城港湾Eular、Stokes 与Lagrange余流的时空特征，以及潮汐和潮流不对称基本特征等进行研究，以期对防城港湾的开发、治理和利用提供科学参考。

1 数学模型

1.1 模型方程

为使建立的数学模型具备良好的地形岸线适应能力，模型方程采用曲线正交坐标系下的控制方程组：

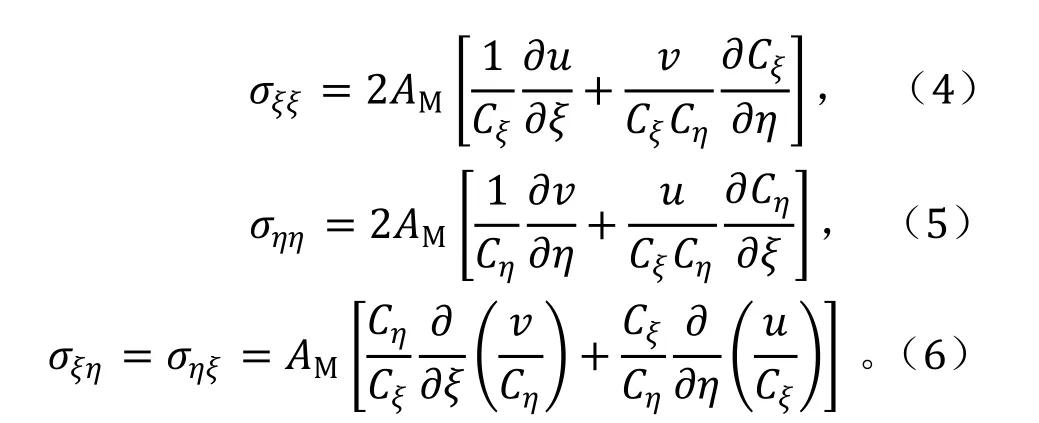
式（1）—（6）中，u、υ 分别为计算平面内ξ、η 方向的速度；Z 为水位；H 为总水深；C 为谢才系数；AM为湍黏性系数；f 为科氏系数。

动量控制方程空间离散采用角输运迎风格式（Corner-Transport Upwind）并结合Van Leer 限制器进行通量限制，时间积分采用可保TVD 性的两步格式。由于防城港湾水深较浅、潮间带宽阔，因此模型中动边界采用窄缝法处理。窄缝法假设在潮滩滩面以下存在宽度随深度指数减小的窄缝，将水体流动引入窄缝之中，实现在固定计算区域的动边界的自动处理[12-13]，避免计算过程中边界变动的人为判断。通过调节窄缝底部宽度和窄缝收缩系数，模型计算中的最小化引水深约为0.01 m。

1.2 计算条件及验证

图1为计算区域的范围和局部水深。模型计算范围西至北仑河口，东边界至108°54′ E附近，南边界约至21°15′ N。西湾顶部的防城江采用多年平均流量作为径流边界条件。外海潮位边界Naotide预报潮位过程给定。网格步长在外海最大约为900 m，在湾内减小至约30 m。模型网格总数为376×333。验证资料为2007年5月18日—19日的实测水文资料，计算区域内防城港湾及附近海域为同时期的实测地形资料。计算坐标采用1954北京系统，基面统一换算至85基面。

表1 为模型验证的统计，其中验证的符合度参数S 的计算公式：

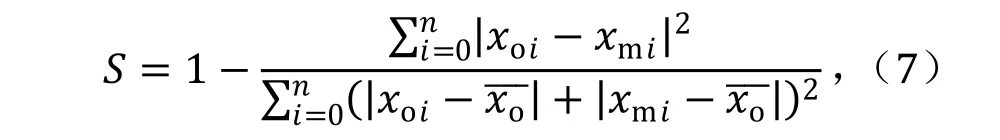
其中，o、m 分别代表实测和模拟，i 为数据点号。

表1 显示，除个别情况以外，相关系数和Skill值均呈现较为满意的结果。其中，F1 点和F4 点的流向验证符合度偏低，主要源于转流前后的计算流向偏差。此憩流时段流速很小，因此这种流向偏差不会对整体模拟效果造成严重影响。F2 点和F3 点的流速偏差略大，可能源于局部细微地形的影响。综合表1 和图1，可见实测和计算的潮位、流速和流向的过程线符合较好，在防城港湾的计算结果能够复演关键测点的潮位、流速和流向。图2—3 为潮位和潮流实测点的对比。

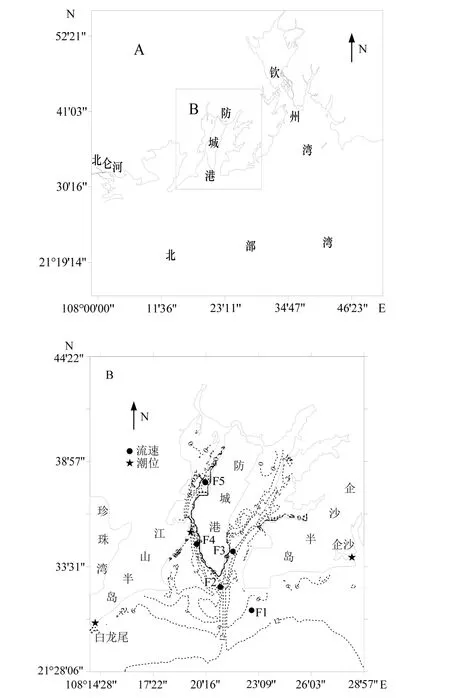
图1 计算区域（A）及防城港湾局部水深（B）Fig.1 Computational domain (A) and topography of the Fangchenggang gulf (B)

图2 潮位验证Fig.2 Comparisons of tidal range

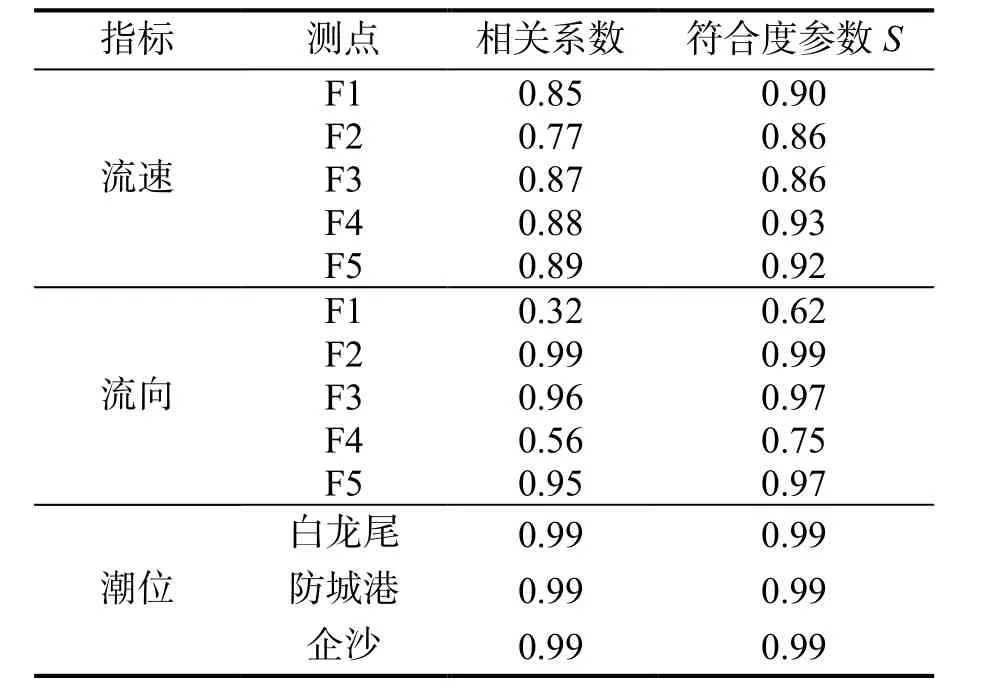
表1 验证指标统计Table 1 Verification indexes

图3 流速和流向验证Fig.3 Comparisons of tidal velocity

2 结果与讨论

2.1 防城港湾余流

图4 为大潮期间的Eular 余流（图4_A）、Stokes余流（图4_B）和Lagrange 余流（图4_C）的平面分布，以及小潮期间的Eular 余流（图4_D）。由图4 可看出，大潮期间，防城港湾的Eular 余流和Stokes余流量值基本相当，但方向相反。二者的量值一般不超过0.1 m/s。防城港湾的Langrange 余流的量值小于Eular 余流及Stokes 余流，规律性亦不如Eular余流和Stokes 余流。总体上，在西湾顶部，由于径流注入，Langrange 余流在深槽部位指向下游；在西湾中部，由于复杂地形的影响而比较散乱。在西湾外部及东湾大部分区域，Langrange 余流在浅水区域指向上游，在深槽区域指向下游。注入防城港湾的河流径流量很小，～O(1) m3/s；而潮差较大（图2），潮汐动力较强。因此，斜压效应导致的河口环流不发育，防城港湾余流形式更符合正压河口海湾的基本水动力特征。

在小潮期间Eular 余流明显小于大潮期间，且Stokes 余流非常微弱，这主要源于在小潮期间的潮差相对于水深要小于大潮期间，即非线性作用较弱，进而潮汐变形的影响亦较弱。此外，由于风生余流的大小及方向主要受制于风应力的情况，从产生机制而言，风生余流在海湾余流中可视为“可线性叠加”的，因此图4 中并未给出风生余流的分布。

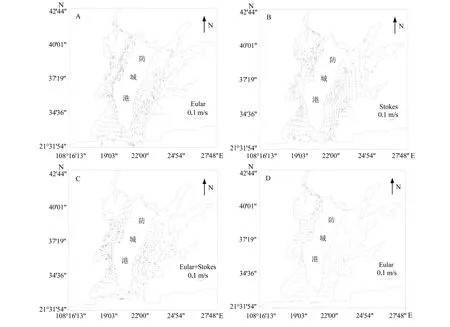
图4 大潮期间防城港湾余流分布与小潮期间Eular 余流Fig.4 Residual currents during spring and Eular residual current during neap

2.2 防城港湾潮汐/潮流不对称的时空特征

Nidzieko[14]提出利用偏度可从统计学角度对潮汐不对称进行定量研究。偏度定义为

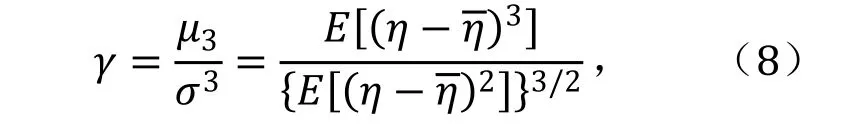
潮流不对称指标定义为

其中，Ufm、Uem分别为最大涨潮流速和最大落潮流速。当δ >0 时，代表涨潮流主导，反之则为落潮流主导。

利用式（8）、（9）在防城港东湾、西湾纵断面（图1 实线）分别逐日计算潮汐和潮流不对称指标。图5 给出了一个月内潮汐和潮流不对称的时空变化。可以看出，在防城港西湾（图5_C），在一个月内潮汐基本呈现落潮主导型不对称，但在小潮期间会出现涨潮主导型（γ ≈ 0.2）。东湾的潮汐不对称型式（图5_D）与西湾相似，但在小潮期间的涨潮不对称较西湾弱（γ ≈ 0.1）。东湾、西湾潮汐不对称另一个相似的特点是潮汐不对称在纵向上变化不大，这应是由于防城港湾长度较小，潮波由湾口向湾顶传播时间很短，湾内潮汐过程近乎同步。防城港西湾的潮流不对称（图5_E）则主要表现为空间的纵向变化，相对而言在时间上变化不大。空间上主要为落潮主导型，但在约7～ 11 km 之间则出现涨潮主导型，此区域为西湾的狭窄水道附近。东湾的潮流不对称（图5_F）在距口门7～ 8 km 附近表现为涨潮主导型，在其它区域则主要为落潮主导型。时间上则呈现很弱的变化。据此可认为，防城港湾的潮汐不对称主要受制于入射潮波，而潮流不对称除了受制于入射潮波，局部地形也起了主要作用。

图5 防城港湾潮汐和潮流不对称时空变化Fig.5 Temporal and spatial variations of tidal and velocity asymmetry

2.3 潮汐不对称分解

式（8）是对总体潮汐不对称的量化。Nidzieko[14]指出，总体潮汐不对称的贡献可分解为不同的满足一定关系的分潮组合而量化各自的贡献。Song 等[15]对Nidzieko 方法进行扩展。基于数值模拟结果，对一个月的潮位过程进行调和分析，进而研究了不同分潮组合对潮汐不对称的贡献。研究得出，在防城港湾对潮汐不对称起第一贡献的为K1/O1/M2分潮组合，这与半日潮海区主要是M2/M4分潮起主要作用不同。第二贡献和第三贡献分别来自K1/M2/MK3和O1/M2/MO3。因此可认为，在防城港湾，虽然对潮汐不对称起主导作用的是天文分潮，但浅水分潮也有不可忽视的贡献。

图6 为东湾和西湾纵断面潮汐不对称成分的沿程变化（一个月）。可以看出，东、西湾潮汐不对称呈落潮主导型，总体上沿程变化有口门向湾内逐渐减弱的趋势。这应为潮波向湾内传播过程中底摩擦导致波形向涨潮主导型方向发展的结果。总体上看，第一贡献（C1）与总体潮汐不对称呈现同样的型式（同号），而第二贡献（C2）、第三贡献（C3）则与总体潮汐不对称相反。在量值上，第一贡献显著大于其它分潮组合，但第一贡献的量值沿程变化不大，其它分潮组合对总体潮汐不对称量值的沿程变化有一定贡献。

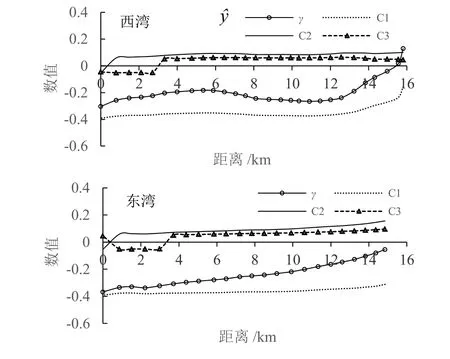
图6 潮汐不对称及其主要成分Fig.6 Tidal asymmetry and its main constitutes

在图6 中，总体的潮汐不对称量值自湾口始向上游，沿程皆为负值。而在图5 中，在小潮期间出现涨潮主导型不对称。这种不同的不对称型式源于统计时段的差异，由于图6 为一个月的统计，图5则为逐日的统计。从量值上来看，图6 显示，西湾总体潮汐不对称量值除湾顶附近以外，基本上为-0.3 左右，较小的沿程变化与图5 中呈现的结论一致。同样，由于统计时间长度的原因，图5 潮汐不对称的量值呈现较为明显的时间变化，而这一特征在图6 中无法体现。图6 显示，东湾总体潮汐不对称自湾口（约为-0.4）向上游湾顶（约为-0.1）逐渐减弱。这与图5 东湾潮汐不对称主要为时间变化的结果有差异。结合图5 和图6，可以认为，时间变化对于潮汐不对称的量化是一个重要的影响因素。从物质输运角度来看，物质输运有其自身固有的时间尺度（如泥沙沉降、污染物降解等），因此，仅基于潮汐调和常数分析不同分潮组合对潮汐不对称的影响忽略了“时间尺度”的意义。

图7 为东湾和西湾纵断面潮汐不对称与其第一贡献的相关关系。可以看出，第一贡献与潮汐不对称呈现极好的线性关系，相关系数均超过0.98。因此可认为，在变化趋势上，第一贡献与总体潮汐不对称是一致的。

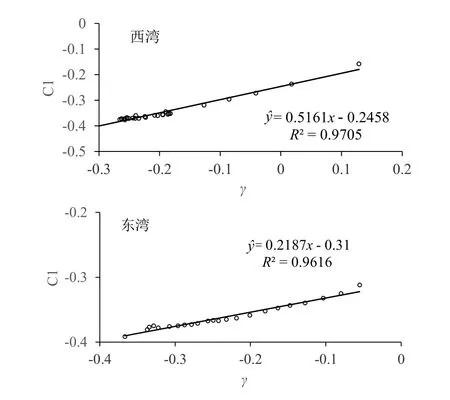
图7 潮汐不对称与其第一贡献成分的相关性Fig.7 Relationship between tidal asymmetry and its first constitute

2.4 潮差、潮汐不对称及潮流不对称的关系

对于潮汐不对称和潮流不对称的关系，一般认为，落潮主导型不对称表现为涨潮历时大于落潮历时，落潮（最大）流速大于涨潮（最大）流速，涨潮主导型不对称则表现相反。图8 为东湾、西湾纵断面沿程的潮差、潮汐不对称以及潮流不对称的相关关系。

图8 潮差、潮汐不对称及潮流不对称的相关关系Fig.8 Relationship between tidal range,tidal asymmetry and tidal velocity asymmetry

由图8 可看出，潮差与潮汐不对称相关关系很弱，除邻近湾顶区域（>12 km）以外，相关系数小于0.2。李谊纯等[16]发现，瓯江口潮汐不对称在大潮期间比小潮期间更显著。但在防城港湾，潮汐不对称与潮差无明显相关关系。笔者推测原因有二：一是，在瓯江口潮汐不对称是由于浅水分潮（M4）的作用，而M4分潮产生与潮差是紧密相关的；但在防城港湾，潮汐不对称主要是第一贡献K1/O1/M2天文分潮组合的贡献。二是，在潮汐不对称的逐日量化中，每日（25 h）并非所有分潮的完整周期。在此情况下，不满足特定关系的分潮之间也可能在逐日统计中对潮汐不对称产生较大影响[17]。潮差与潮流不对称似无明显关系，相关系数沿程变幅极大（-0.8～ 0.6），这可能是源于复杂的地形特征。然而，潮汐不对称与潮流不对称之间存在密切的相关性，相关系数在东、西湾均约为0.8，这与以往研究中的普遍性表述基本一致。