基于ACT-R理论的“双曲线及其标准方程”教学设计
2021-07-24江苏省太仓高级中学215400
江苏省太仓高级中学 (215400) 陆 庭
近年来,问题解决中的迁移成为认知心理学的关注热点.问题解决中的类比策略表现了学习迁移在问题解决中的作用.样例(指蕴含了一般概念、原理或方法的例子)在问题解决和迁移中起着至关重要的作用,因此,样例学习研究的价值和重要性就不言而喻了.如何设计样例结构或创设样例学习系统减少负面影响,更好地发挥样例的作用是值得我们研究的课题.本文以《双曲线的标准方程》一课为例,阐述基于ACT-R理论的教学设计对数学课堂教学带来的改变与影响.
1. ACT-R理论的要义
ACT-R理论(理性思维适应性控制理论,Adaptive Control of Thought-Rational)是一个人类认知理论,在1976年由美国人工智能专家和心理学家安德森等人首次提出及建立理论模型.该理论试图理解人类如何获得和组织知识以及如何产生智力活动,其研究进展基于神经生物学研究成果并从中得以验证.安德森团队多年来致力于有关学习、记忆与大脑神经的研究,在长时间的探索中孕育出了ACT-R理论体系.ACT-R理论被称为是“学习与认知的简单理论”,其基本观点是:复杂认知是由相对简单的知识单元所组成的,而这些知识单元是通过相对简单的原理获得的.该理论在有关教育、学习的领域得到广泛的关注与应用.其中,学习迁移为该理论与实际应用主要的契合点.迁移是一种长期受到人们关注的心理现象,它的基本含义是在先前的学习(或训练)中获得的知识和技能,对学习新知识、新技能或解决新问题所产生的影响.
2. ACT-R理论指导下的教学设计
2.1 整体架构,把握方向
著名数学家波利亚认为:“学习任何东西最好的途径是自己去发现.”双曲线的定义和标准方程与椭圆很类似,学生已经有了一些学习椭圆的经验,所以将椭圆的知识设为样例,让学生将研究椭圆的知识与方法迁移到双曲线的学习中来,是符合ACT-R理论.本节课笔者采用了“自主探究”式的教学方式,重点突出以下两点:一是以类比思维作为教学的主线;二是以自主探究作为学生的学习方式.
ACT-R理论提出认知层级的分解,将一个宽泛的最终认知分解为一个个小的子认知来完成,通过学生已有的现状知识进行认知的合理分层,设计出一个层次鲜明、易于接受的教学过程(图1).教师通过给学生制定的学习指南,让学生了解本节课的教学流程,引导学生有目的的自学,让学生明确课上要展示的成果,极大的激发学生学习的积极性及创造性,培养他们积极的学习态度和浓厚的学习兴趣.

图1
2.2 样例选择,明确目标
ACT-R理论认为知识技能的获得通常要经历三个阶段:认知阶段、联合阶段和自动化阶段,完成这三个阶段有两条途径:一是用某种一般的解题策略来解决这个具体问题而形成的新的知识;二是通过类比将另一个问题的策略应用于这个问题而获得新的知识.在第二种途径中,样例发挥着重要的作用.当已有的知识不能解决当前问题时,大脑会先搜寻之前解决的类似问题的样例,以此作为类比源,形成能解决当前问题的新的技能.教师给出历史上数学家推导椭圆标准方程的一般方法(样例),让同学们欣赏并借鉴一种方法来推导双曲线的标准方程.
样例一:和差术
“和差术”最早可以追溯到古代两河流域的古巴比伦时期(公元前2000~1600年),是在古巴比伦的泥板上被发现用来解决二元一次方程的一个很巧妙的技巧.法国数学家洛必塔在18世纪首次利用“和差术”推导出了椭圆的标准方程.

样例二:“平方差”法
19世纪英国数学家赖特(爱德华·梅特兰·赖特爵士)率先使用此法推导出了椭圆的标准方程,随后,同世纪的爱尔兰数学家哈密尔顿及美国数学家温特沃斯也都采用了同样的方法.

样例三:“分子有理化”法
“分子有理化”法是现行的俄罗斯数学教材中使用的方法.

正所谓“学史使人明智”.数学是人类最古老的科学知识之一,它的发展经历了很多的坎坷,让学生欣赏历史上椭圆的标准方程的推导过程,能让学生更好的理解推导中所使用的方法及出现的问题,进而迁移到双曲线的标准方程的推导过程中来.
2.3知识迁移,推陈出新
ACT-R理论实际上是“做中学”与“例中学”的理论,它以学习迁移为该理论与应用的主要契合点.通过将先前学习中获得的知识和技能迁移到新的知识,以获得学习的新的体验、新的技能或解决问题的新的方法.学生课前仿照椭圆标准方程的推导过程,推导了双曲线的标准方程,并在课上分组展示.


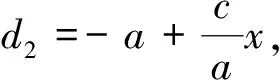
同理可以证明d1 让学生类比数学家的方法来推导双曲线的标准方程,使知识获得迁移,能更大的激发起学生的学习兴趣,调动学生学习数学的积极性,培养学生正确的数学学习习惯及数学思维方式,提高学生的数学修养.并且在推导的过程中潜移默化的将类比的思想渗透到学生的思维中去,让学生感受到类比的强大力量,体会到类比带来的成功的喜悦. ACT-R理论中,知识的获得主要依靠类比,类比发生的一个重要前提就是要有一个解决某个目标的情境,即学生要有一个解决问题的意愿.然而《双曲线的标准方程》一课中存在大量的运算,推导过程较为繁琐,学生不愿去计算,由学生自行推导双曲线方程或者师生共同协作完成双曲线的标准方程的推导,学生经历了推导的过程,但是推导过程里面到底会有哪些问题,会出现哪些困难,为什么要这样推导学生根本不太明白,也不愿意去弄明白,学生必然会觉得枯燥乏味.因此教师在样例的选择上应挑选贴近学生认知实际的椭圆的标准方程及与学生感兴趣的历史上成功推到椭圆标准方程的方法,强化学生发现问题、探究问题、解决问题的能力. ACT-R理论中,类比发生的另一个重要前提就是有一个解决类似目标的范例.这就要求椭圆样例的本身要能真正具有示范的功能,能促进知识的迁移,即在问题内容、思路探索、解决方法以及运算步骤四个方面上具有典型性,能够准确地作为学生解决相似问题时的类比范例.事实证明,学生通过类比椭圆标准方程的推导过程,能够自主探究双曲线的标准方程的推导过程,整个课堂学生的主体性地位体现无疑.教师根据ACT-R理论在课堂教学中创设了有利于张扬学生个性的“场所”,课堂已然不是传统的课堂,已经成为学生表演的舞台,让学生在愉悦的气氛中激扬生命,展现个性. ACT-R理论指导的教学设计需要经历三个阶段八个环节,分别为:第一阶段陈述性阶段,让学生通过样例抽象出数学问题,对目标知识进行层级分解,初步感知数学知识,包含引入样例、明确目标、层级分解、形成新知四个环节;第二阶段程序性阶段,让学生通过对原有数学知识进行加工,形成新的技能,通过练习与强化,巩固新知,包含形成初步技能与合成复杂技能两个环节;第三阶段自动化阶段,将知识技能融入特定问题情境中,让学生知道在什么情境中可以使用这些技能,包含匹配问题情境和自动解决问题两个环节.因此,将整个教学过程分层分解到课前、课中、课后的各个环节中,组织课堂活动逐步推进,不仅降低了学生学习的难点,符合学生认知的发展过程,而且提高了学生自主学习的时间,将学生已有的知识与新的知识建立联系,使学生获得新知的同时还体验了整个数学的活动经验,促进了知识的迁移. 希尔伯特曾将教学描述为“在课堂中围绕内容并促进学习目标达成的师生、生生活动”.课堂中的合作展示,不仅仅让学生展示双曲线标准方程的推导过程,更让学生来说清楚“背后的故事”,加深学生对类比过程的理解与认知.学生的小组合作,绝不是要消除学生的差异,而是让他们能够在小组中找到适合自己的角色,调动他们原有的知识经验,运用各自独特的思维方式,取长补短,相得益彰,发挥集体的智慧能更好的打开思路去发现问题、解决问题,让学生的主体性、能动性、独立性得到不断的发展和提升,促使他们更好的发展. 按照ACT-R理论,理解可以导致更多的灵活性,也容易将知识、方法与技能迁移到新的情境中去.在学生解决新的问题时,更多的倾向于知识的迁移,让新的方法的获取变得更为的简单.在知识的迁移过程中,可以将学生的注意力引向与知识相关的部分,有效防止了“错误学习”,缩短学生的认知过程,减轻认知负担,提高认知效率,形成新的理解.因此加深知识的理解在数学学习中变得尤为重要,它必将极大的调动学生学习的主动性和积极性,有助于培养学生良好的思维能力和提高解决问题的能力.

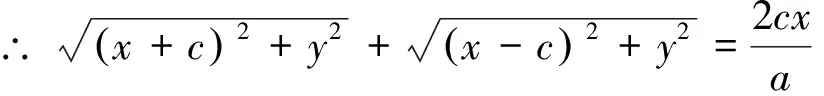



3. ACT-R理论对课堂教学的反思与总结
3.1通过类比学习,明确知识目标
3.2 通过分层学习,促进知识迁移
3.3 通过对比学习,加深知识理解

