经历概念的形成过程 积累基本活动经验——以“平面向量的概念”教学为例

福建省福州市闽清高级中学 (350800) 林朝晖

积累基本活动经验是数学学习的基础，是提升学生数学核心素养的重要标志.数学基本活动经验，指的是学生在经历数学学习活动的过程中所获得的感受、体验与认知.对于学生来说，数学活动经验需要在“做”中获得，在“思”中提升，在“悟”中迁移.因此，教师应引导学生主动、积极参与数学学习活动，让学生经历实践操作的过程，在观察操作中把感受提升为经验；让学生经历内化、反思等活动过程，从而提炼出具有数学本质的基本活动经验.笔者以高中数学新教材(人教A版)必修第二册“平面向量的概念”的教学为例，谈谈积累数学基本活动经验的教学实践与思考.

1 在概念引入处唤醒基本活动经验

概念的形成过程是对概念进行归纳、抽象、概括的过程，经验性认识常常是内隐的，教师应遵循由感性到理性、由具体到抽象这一学生的基本认知规律，创设恰当的问题情境，帮助学生搭建学习新知的“脚手架”，把一些抽象的知识形象化，才能激发学生的活动动机，帮助学生从“冰冷的美丽”中真正感受和体验数学家发明创造时的“火热思考”，从而唤醒学生的基本活动经验.

教学片断1 创设情境，抽象概念

问题1 某景区内有三个小岛A,B,C，几位游客乘观光游艇先从A到B体验双向索道,再从B至C感受水上滑梯,请从物理角度谈谈在此观光过程中所涉及到的量.

追问：请同学们回顾物理中学过的位移，说说距离与位移这两个量有什么不同？

师生活动：引导学生归纳得到位移是矢量,不仅有大小,还有方向，而距离只有大小，没有方向.

设计意图：从熟悉的问题引人,引导学生把问题1的内容抽象成数学问题，引出向量的原型“位移”.

问题2 大家能再举出几个既有大小，又有方向的量吗？

师生活动：学生举出如下例子，如速度，加速度，重力、浮力等.

追问：能否举出只有大小、没有方向的量？(意图通过对比，凸显出向量的两个要素.)

生：身高、体重、面积、体积……

师：在数的概念的学习中，我们从一本书、一支笔、一付眼镜……抽象出了只有大小的数“1”.类比数的概念，可以对大小和方向两个要素的量进行抽象(如浮力、重力、速度、加速度等)，得到一种新的量，我们将这些量叫做向量.

设计意图：通过引导学生列举实例，提炼出事物的本质属性，从而抽象、概括出“向量”的概念.

问题3 请大家说一说，我们可以按照怎样的思路研究一个新概念？

设计意图：类比实数的教学，引导学生归纳出研究一个新概念的基本思路：抽象出事物的本质属性——给出定义——用符号表示——认识特殊对象——研究特殊关系——数学应用.

“平面向量的概念”教学内容涉及到多个概念的形成、同化和命名.本环节通过创设熟悉的生活情境,引导学生主体参与，唤醒学生基本活动经验，让学生在活动中初步感受新知，并在脑海中形成新知的表象.教师通过引导学生运用类比、特殊化等思想方法“赏玩”新概念，引导学生提炼研究新概念的一般思路，让学生在活动中体验和感悟学习新概念、研究新问题的方法，为后续的学习起到了“导游”作用，发展了数学抽象素养.

2 在观察操作中构建基本活动经验

学生在参与和经历数学学习活动的过程中，可以直接获得一些数学活动经验，但如果这些经验仅仅停留在感性的层面，只是肤浅的经验，需要教师运用教育智慧引领学生揭示感性经验背后理性的力量.因此，教师应引导学生通过“做”探索知识和规律，在实践活动中理解和感悟数学，直至获得某些“再创造”的思维活动成果.这样，才能使学生生成的基本活动经验更加丰富、深刻，更“接地气”，从而实现“感性经验”向“理想经验”的提升.

教学片断2 形象表示，深化理解

问题4 为了方便起见，学习了向量概念之后，通常需要用符号表示.大家想一想，如何表示一个实数?

生1:可以用小写英文字母表示实数,如a,b,c…

师:还可以怎么表示？

生2:画数轴表示,如图1，AB=1,OB=2.

图1

师：实数可以这样表示，那平面向量该怎样表示呢？

设计意图：让学生在活动中提炼出符号化语言，培养学生的符号化意识.

师生活动：学生讨论，然后请两位同学板书，师生讨论并完善.

追问1：这两位同学都想到用有向线段来表示一个向量(如图2)，这是向量的“形”的表达方式，也可用符号表示，我们应该怎样用符号表示呢？

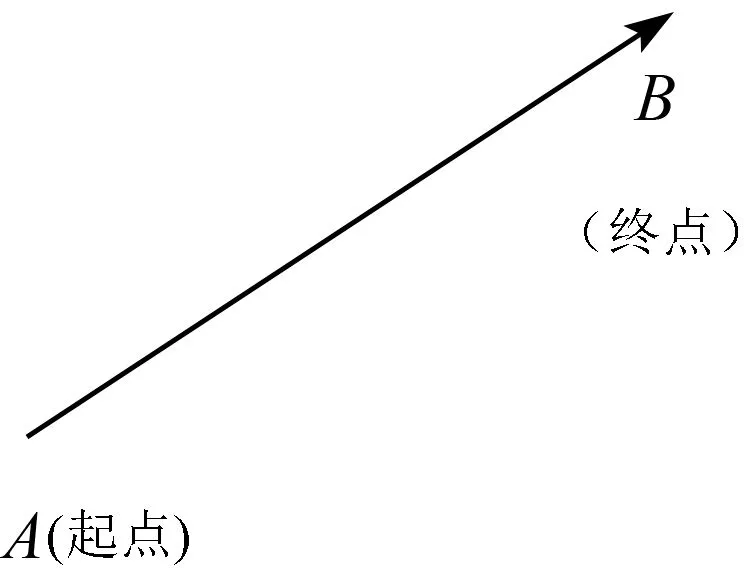
图2

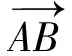
师：生3将向量和线段进行类比，非常好！类比思想有助于今后的学习.

设计意图：进一步强调向量的方向性，深化学生对向量概念的理解.

教学片断3 认识特殊，引出关系

问题5 大家知道，有两个很特殊的实数0与1,是否也有特殊的向量呢？

生5:有，长度为0与长度为1的向量就是特殊的向量.

设计意图：让学生通过0与1这两个特殊实数，类比引出零向量、单位向量的概念.

追问1：零向量与单位向量的方向该怎样规定？

追问2：若将平面上所有的单位向量平行移动到同一起点，想想这些单位向量的终点轨迹是什么？

设计意图：紧紧围绕学生容易忽略的向量的方向性，渗透规定零向量方向任意的合理性.通过追问，引导学生进行观察、分析，突破单位向量的方向这一难点.

追问3：刚刚已经学习了特殊模长的向量，是否具有特殊关系的向量呢？

问题6 说出图3中各个向量的模，其中哪些向量是单位向量？

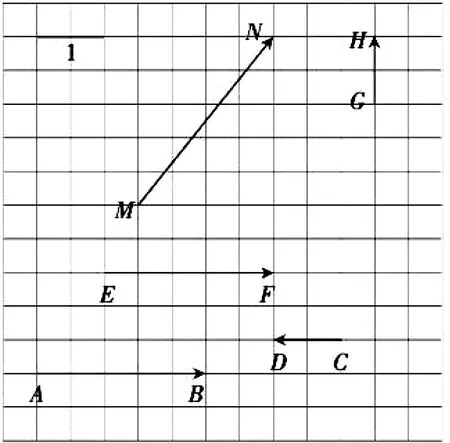
图3

设计意图：通过活动，深化学生对向量的模与单位向量的理解.

追问2：平行向量从方向上刻画了向量的关系，它们与大小是否有关？

追问4：两个向量相等，是否与其位置有关？

师：相等的非零向量都可以“自由平移”，说明了向量是可以平行移动的“自由之躯”，与向量的起点无关.

设计意图：通过直观感知、教师启发，引导学生参与向量概念的定义过程，归纳出平行向量、相反向量、相等向量等概念，使概念成为学生观察、比较、抽象、概括后的自然产物，符合学生认知规律,也为引出共线向量埋下伏笔.

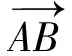
设计意图：共线向量是学生学习的难点,问题7意在引导学生体会共线向量就是平行向量，自然获得共线向量的定义.

以上探究过程，始终以学生为主体，以问题串为主线，启发学生类比实数概念的学习，通过操作、分析、思考、讨论，逐步抽象概括出向量的有关概念.在活动过程中，教师注重渗透数学思想方法，并运用类比的思想、联系的观点引导学生利用已学的数学知识和数学基本活动经验探索向量的有关概念.随着学习活动的逐步推进，部分学生能主动地运用类比的思想进行探究，自然获得与向量有关的基本概念，从而积累了“数学化”的活动经验，提升了直观想象、数学抽象、逻辑推理等数学核心素养.

3 在反思感悟中积累基本活动经验

数学知识的类比性使得学生所积累的基本活动经验具有迁移性，这些经过学生内化、感悟的经验是学习新知的生长点.因此教师应创设数学学习活动所需要的情境，并给学生留足反思感悟的时间，让学生自主参与到数学学习活动中，经历内化、反思等活动过程，这样有利于数学知识在深度思考中得到提升与完善，有利于建构系统化的认知体系.长此以往，学生就会积淀丰富多样、“生长力强”的数学基本活动经验.

教学片断4 辨析概念，深度思考

问题8 下列说法是否正确，请说明理由.

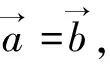
(2)单位向量是相等向量；

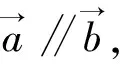
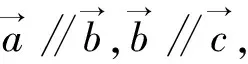
设计意图：针对学生可能产生的理解偏差，让学生辨析，强化他们对概念本质的理解，积累活动经验.

问题9 设O是正六边形ABCDEF的中心.

图4

图5

设计意图：让学生进一步体会共线向量、相等向量的含义，深化相等向量和共线向量的联系与区别.

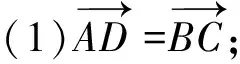
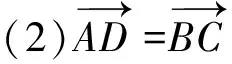
教学片断5 反思总结，提升高度

问题11 本节课学习了哪些内容？你能应用思维导图对所学的内容进行梳理吗？

问题12 本节课学习中运用了哪些数学思想方法？

设计意图：引导学生梳理所学知识，深化向量有关概念，为学习向量的运算铺垫；另一方面，引导学生感悟数学思维方式、数学思想方法，获得研究新概念的基本套路.

对上述问题的辨析与反思，发挥了一般观念的思维引领作用，是学生对平面向量概念的再认，对向量概念形成过程中体现的研究方法、研究经验的总结反思，有利于建立更高层次的认知结构，从“经历”走向“经验”.

总之，数学教学需要让学生亲身参与数学学习活动，在“做”、“思”与“悟”中不断积淀基本活动经验.数学课堂教学应该为学生创设具有丰富性和挑战性的探究活动，引导学生通过观察分析、抽象概括、逻辑推理、反思总结等思维活动，促进个体经验的交流与融合，从而“生长出”新的数学活动经验，让数学核心素养的发展更加枝繁叶茂.