“正弦定理”教学设计与课堂纪实*
2021-07-24江苏省高邮中学225600黄桂君江苏省高邮市城北中学225600陆永宏
江苏省高邮中学 (225600) 黄桂君 江苏省高邮市城北中学 (225600) 陆永宏 桂 楚
本文是笔者在特级教师牵手乡村(高邮市三垛中学)教育活动中送培送教的一节公开课教学设计与课堂真实情况的回顾记录,有意将课前准备(备课)的与课堂中真实发生的做一次比较,并穿插谈点感受以及正余弦定理哪一个先安排讲授“好”的体会.
一、教学目标
1.掌握正弦定理及其证明;
2.能够运用正弦定理解决一些简单的三角形边角度量问题以及与测量有关的实际问题.
二、教学过程
1.问题情境
如图1,要测量一个不可逾越障碍物两侧且相互看不见的两点A、B间的距离,已知点A在观察点C南偏东60°方向,点B在C南偏西45°方向,AB为东西方向,BC=10,则A、B两点间的距离是多少?(情境选的是该学校旁边的著名的河流与建筑,学生感觉亲切.同时也是苏教版新教材例1的问题)

图1
紧接着设问:能否不通过解直角三角形而由已知△ABC的边和角直接求出AB呢?说明为什么要学习这个新知识的必要性,导入新课.(注:最后再回过头来重新解,前后呼应)
2.讨论
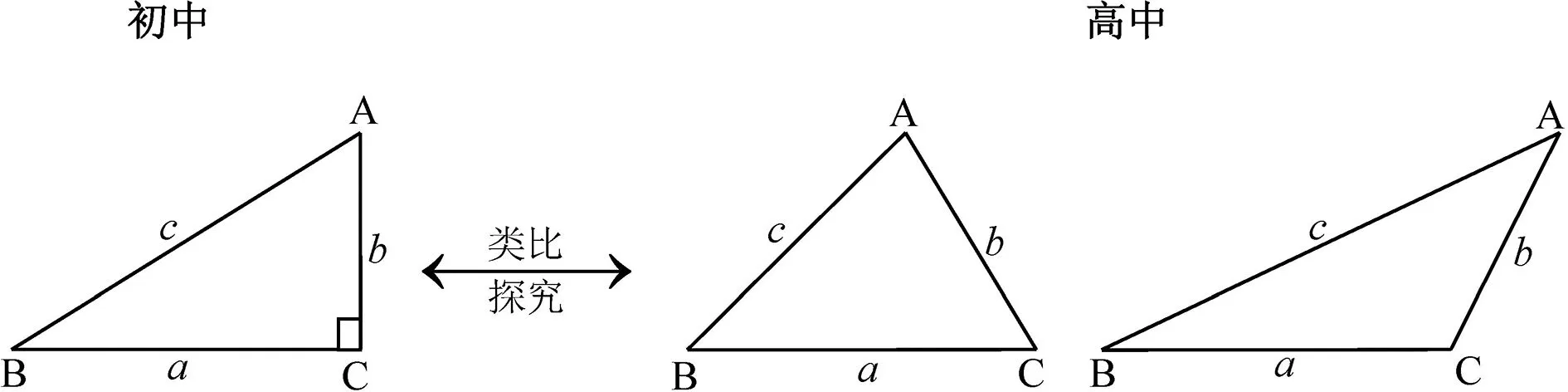
图2
下面的问题尽量的让学生说或写.(在黑板左右对应图形下方分别板书)
(1)关于角:任何三角形中A+B+C=π(180°)(共性)(这里指出三角形中角与边的简写,如果先学的是余弦定理就不再提)
直角三角形中,A、B互余,sinA=cosB,cosA=sinB,tanA·tanB=1.(学生没有说到的三角关系式尤其是正切,老师提问,效果还好)
思考:若C是△ABC中最大(小)的角,则C的取值范围是.
结论是60°≤C<180°(0° (2)关于边:任何三角形中,a+b>c,a-b 直角三角形中,c2=a2+b2(勾股定理). 思考:非直角三角形中,c2=a2+b2+?(告诉学生将在后面探究学习,引起兴趣.如果先学的是余弦定理就不设计了) 以上两点快速而过,重点是下面的边角关系. (3)边角关系(探索):任何三角形中,C>A⟺c>a,b 注:课前不要求学生预习,课上也不允许学生翻看教科书(在苏教版新教材中也没有上述内容).老师接着在黑板右边斜三角形图形的下方写上一个醒目的“?”(触及课题). 猜想:对于一般的三角形也能成立吗? 图3 引导学生证明.假设猜想成立,则有asinB=bsinA,csinB=bsinC. 设问(循序渐进):在图形中能找到asinB,bsinA;csinB,bsinC的几何意义吗?让学生思考并上黑板上画(添加辅助线).这里教学重点得到了体现,难点得到了突破. 引导学生联系初中熟悉的直角三角形,构造直角三角形,类比发现.(实际情况是,在锐角三角形中学生能很快画出高线,在钝角三角形中有了难度,但在老师的启发下,还是画出来了.要多让学生动脑、动手,积极参与) “等高法”(证法1):csinB=bsinC,……(注意对角C分类讨论)其它同理可得.事实上,根据图形我们还能发现什么?引导学生大胆探究,发现:a=ccosB+bcosC,……(射影定理)(顺便带出的副产品,本节课不讨论)得出 正弦定理(文字语言):三角形的各边和它所对的角的正弦之比相等. 我们的教学要“以学生的学习为中心来组织教学”.重结果,也要重过程!讲推理,更要讲道理!让学生思考探究一些他们的能力能够“够得着”的问题,注意重视培养学生的数学核心素养. 例1(苏教版新教材P90)在△ABC中,A=30°,C=100°,a=10,求b,c(精确到0.01).(解答需要用到计算器) 变式将100°改为105°?让学生板演,即开始的情境问题,前后呼应.教师板书详解示范. 例2(苏教版新教材P91例2的变式,仅仅改了数据,目的方便学生不需要用计算器就能得出结果,但问题的教学功能没有变)根据下列条件解三角形(指出解三角形的概念). 让学生板演、分组练习比较. 先让学生独立思考求解,发现问题后再和学生一道寻找出错原因(本节课不要急于讨论三角形有几解的问题). (1)几何画板演示.指出教科书P95第10题几何画板得到的相同的比值7.33有什么几何意义? 注:到这个时候才利用多媒体演示验证,巩固新知,而非一开始就给出.因为重要的是引导学生怎么发现的,验证或直接告知结论过于简单直接. (2)尝试用其它方法证明正弦定理: ①几何法(证法2,由上述比值始终相同激发思维而产生) a=2RsinA 另,对于余弦定理可自然的启发性设问:求两点间的距离(线段的长度)在你印象中有哪些数学思想方法?在这些方法中自然想到有一种方法向量法——转化为求向量的模.(以上思考课堂上先提出来,后安排作业中课外自主探索)有时候抛弃思维定势围绕核心又结合实际的做法,谁说不也是一种创新呢? 本节课让我们感悟到,要学会用数学的眼光去观察(看世界);会用数学的思维去思考;会用数学的语言去表达;会用数学的知识去解决. (这正是数学学科核心素养的特质) 1.江苏凤凰教育出版社《普通高中教科书 数学必修第二册》(2020年7月第1版)P92练习1,2,4;P94习题11.2.1,7. 2.尝试用向量证明正弦定理. 结语:在教学设计中,要抓住数学内容的本质、了解学生的认知规律,创设恰当的情境、提出合适的问题,启发学生独立思考、鼓励学生交流表达,在掌握知识技能的同时理解数学的本质,形成和发展数学核心素养.我们教学工作的重心是努力“将课本上知识的学术形态转化为教师的教育形态、学生的学习形态”,即“唤醒”数学知识,而不是给予,一个好的老师,就是这样把知识唤醒给学生看.这种转化工作谁做的好,谁的教学就有效!
3.引导学生在直角三角形中发现
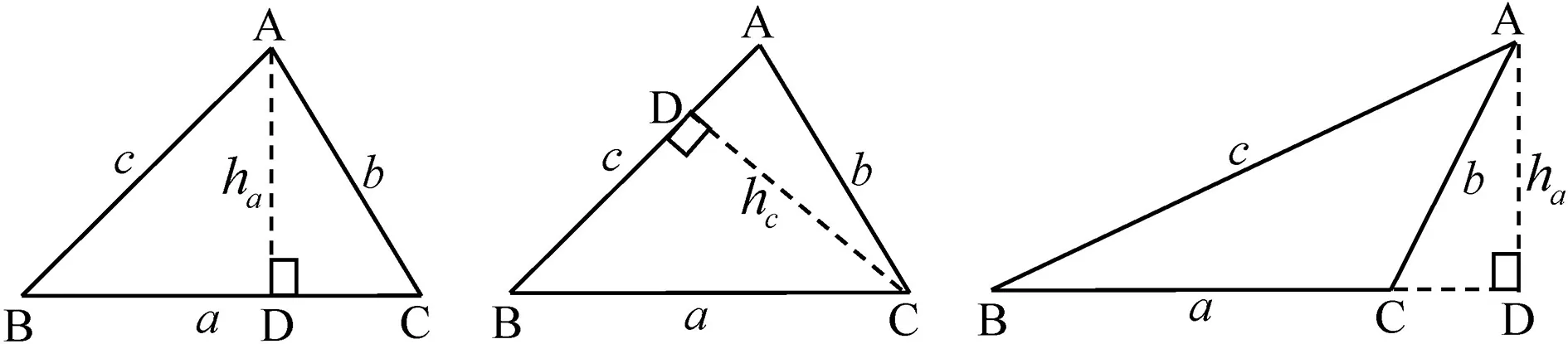
4.应用
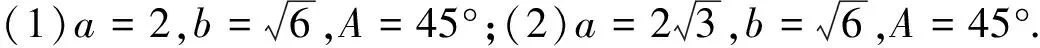
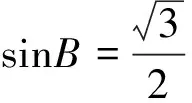


5.思考

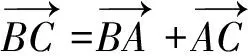
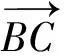
6.小结
三、课外作业
