基于移动荷载谱的桥梁竖向自由振动最大响应研究
2021-07-22李锦华张焕涛蓝声宁
李锦华, 张 耀, 张焕涛, 蓝声宁
(1. 华东交通大学 土木建筑学院,南昌 330013; 2. 华东交通大学 土木工程国家实验教学示范中心,南昌 330013;3. 北部湾大学 建筑工程学院,广西 钦州 535011)
国内外研究人员已对列车作用下的桥梁振动问题进行了广泛的研究,甚至考虑了风荷载和列车制动力影响下的桥梁纵、横向振动问题[1-2]。随着我国高速铁路的大量建设以及铁路系统的升级,高速列车引起的桥梁振动响应问题也日益突出,尤其是关于列车荷载引起桥梁共振响应的问题[3]。
对于列车荷载引起的桥梁共振响应问题,研究人员采取了各种方法进行分析。对于实际列车作用下桥梁的振动响应,需考虑列车-桥梁的耦合作用[4-5],然而采用该方法的研究只能通过数值模拟来分析桥梁跨度,荷载轴距及移动速度等因素的影响[6]。这种分析方法虽然贴合于工程实践,但求解过程较为复杂,通用性不高,因此为了工程实际的通用性,很多学者采用解析的方法求解各类桥型结构的共振机理。Yau[7]根据移动荷载引起简支梁的共振公式,采用类比法确定高速列车作用下连续桥梁的多个共振峰值;再基于有限元方法研究了跨数对连续梁桥冲击作用的影响。Wang等[8]通过振型分析法分析了列车作用下两跨连续梁的振动响应,并得到了不同于简支梁的两个共振速度,且考虑了阻尼比、桥梁跨度对振动响应的影响。吕龙等[9]采用等效纵向荷载研究了移动荷载作用下斜拉桥的纵向振动机理,推导出纵向共振速度的估算公式。
其中对于列车荷载作用下简支梁桥的共振问题一直是研究热点。Yang等[10]将列车荷载简化为等轴距的两个子系统,通过解析方法确定了控制桥梁动力响应的关键参数,并根据移动荷载产生的桥梁响应曲线给出了有效抑制桥梁共振的优化设计准则。李慧乐等[11-12]从理论推导和分析实例,研究了车桥系统的共振机理和发生共振的条件,并推导出移动荷载(单个集中力、等轴距移动荷载列及非等轴距移动荷载列)作用下的桥梁振动响应解析解,获得了移动荷载作用下简支梁发生共振及两类消振响应下车速计算公式。张铎等[13]研究一系列移动简谐荷载作用下简支梁竖向动力响应,首先理论推导出了桥梁响应的解析表达式;然后通过数值模拟分析了荷载移动速度、谐振频率以及桥梁阻尼比等参数对桥梁共振的影响。然而当移动荷载以共振速度匀速通过简支梁后,并不能引起桥梁的最大响应[14-16]。
目前,对于桥梁振动理论的研究主要是从时域角度进行分析,然而频域相对时域而言,直观且无需求解微分方程。为了直观有效地分析桥梁自由振动最大响应的影响参数,建立起各参数与桥梁自由振动最大响应的关系,本文将考虑列车荷载为两轴车辆荷载,从频域角度出发,采用傅里叶变换推导出两轴车辆荷载通过桥梁时的移动荷载谱及桥梁振动响应谱,再通过对移动荷载谱的分析,获得引起桥梁自由振动最大响应时的移动荷载速度,并通过算例验证相关理论研究的有效性。
1 移动荷载激励下的桥梁运动方程
为了分析列车速度、荷载轴距对桥梁振动响应的影响,将列车荷载考虑为两轴集中力荷载模型,如图1所示。集中力荷载大小为P,轴距为d,该荷载以速度v匀速行驶在跨度为L的桥梁上,该桥梁的运动方程可表示为
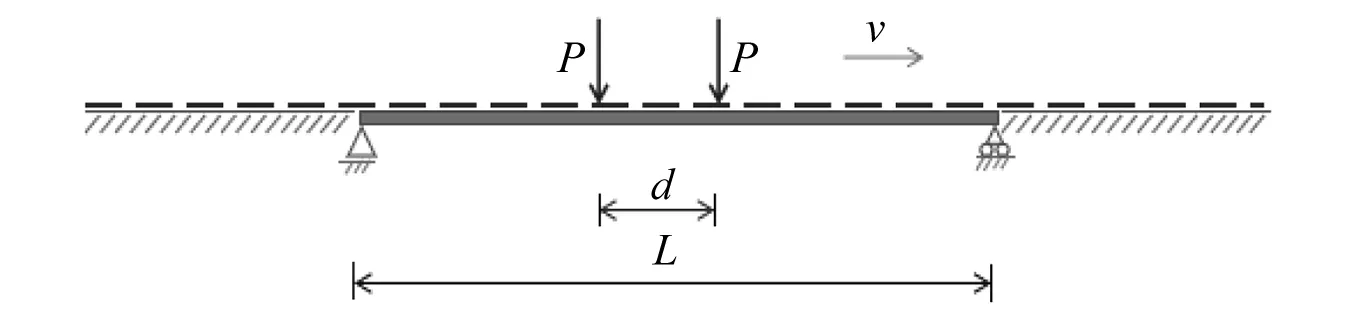
图1 桥梁及移动荷载模型
(1)
式中:qj为桥梁第j阶振型的广义坐标;m为桥梁单位长度质量;ωj,ξj分别为桥梁的第j阶自振频率和阻尼比;fj(t)为两轴移动集中力荷载产生的第j阶振型荷载,其表达式为
(2)
式中,S(t)=S0(t)-S0(t-L/v)可判断移动集中力是否作用在桥梁上,S0(t)为Heaviside函数。
本文对两轴移动荷载作用下桥梁的运动方程编写了相关求解程序,算例采用了文献[17]中的桥梁及两轴移动荷载数据,如表1所示。当移动荷载以速度100 km/h匀速通过桥梁时,桥梁跨中位移振动响应如图2所示。由图2可知,本文运用振型叠加法计算的桥梁跨中竖向位移振动响应,与文献[17]中的数据相互吻合,验证了上述运动方程及计算程序的正确性。

表1 桥梁参数及荷载参数
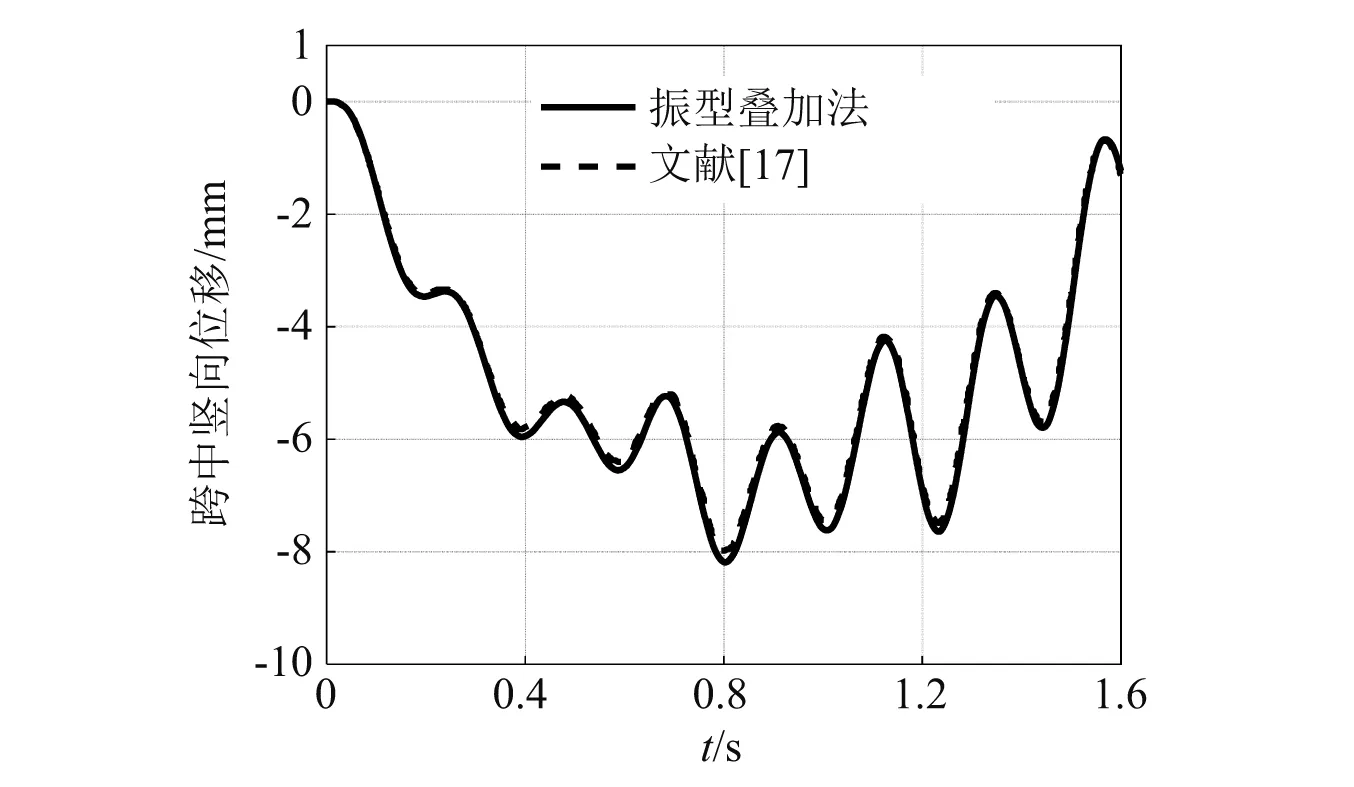
图2 桥梁跨中竖向位移响应
2 频域分析法
目前,对于移动荷载作用下桥梁自由振动响应幅值的分析,主要采用时域数值计算方法,而该方法对运动方程需要进行反复计算求解。为了快速有效地分析移动荷载作用下桥梁自由振动响应,本章将建立有效的频域分析法对此进行分析。
对式(1)两边进行傅里叶变换可得桥梁竖向位移的第j阶模态响应分量
Qj(ω)=Hj(ω)Fj(ω)
(3)
于是,移动荷载引起的桥梁振动位移响应谱Y(ω)为
式中:φj(x)为桥梁的第j阶振型函数;Hj(ω)为传递函数
(5)
Fj(ω)为第j阶振型移动荷载谱,可由式(2)进行傅里叶变换得到
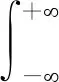
当振型为奇数时,即j=1,3,5,…,第j阶振型移动荷载谱为
(7)
当振型为偶数时,即j=2,4,6,…,第j阶振型移动荷载谱为
(8)
考虑桥梁的第一阶振型,并忽略桥梁结构阻尼的影响,根据式(4)可得移动荷载激励的桥梁振动位移响应谱为
Y1(ω)=H1(ω)·F1(ω)·φ1(x)=
(9)
对其取模,即桥梁位移响应幅值谱|Y1(ω)|
(10)
由式(10)中振型函数sin(πx/L)的表达式可知,当x=0.5L时,即在桥梁的跨中位置会产生最大值;而根据传递函数|H1(ω)|可知,当移动荷载激励频率等于桥梁自振频率时即ω=ω1,传递函数达到最大值。此时,跨中桥梁位移响应幅值谱的最大值,仅与移动荷载幅值谱的最大值有关。其移动荷载幅值谱大小为
(11)
令κ=v/ω1L为移动荷载无量纲速度,γ=d/L为移动荷载轴距与桥梁跨度的比值,简称轴跨比。因此,式(11)可写为
(12)
根据式(12)可知,当ω=ω1时,移动荷载幅值谱仅含有两个未知变量κ,γ。实际中轴跨比γ通常小于2,因此本章考虑γ在0~2内。
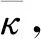
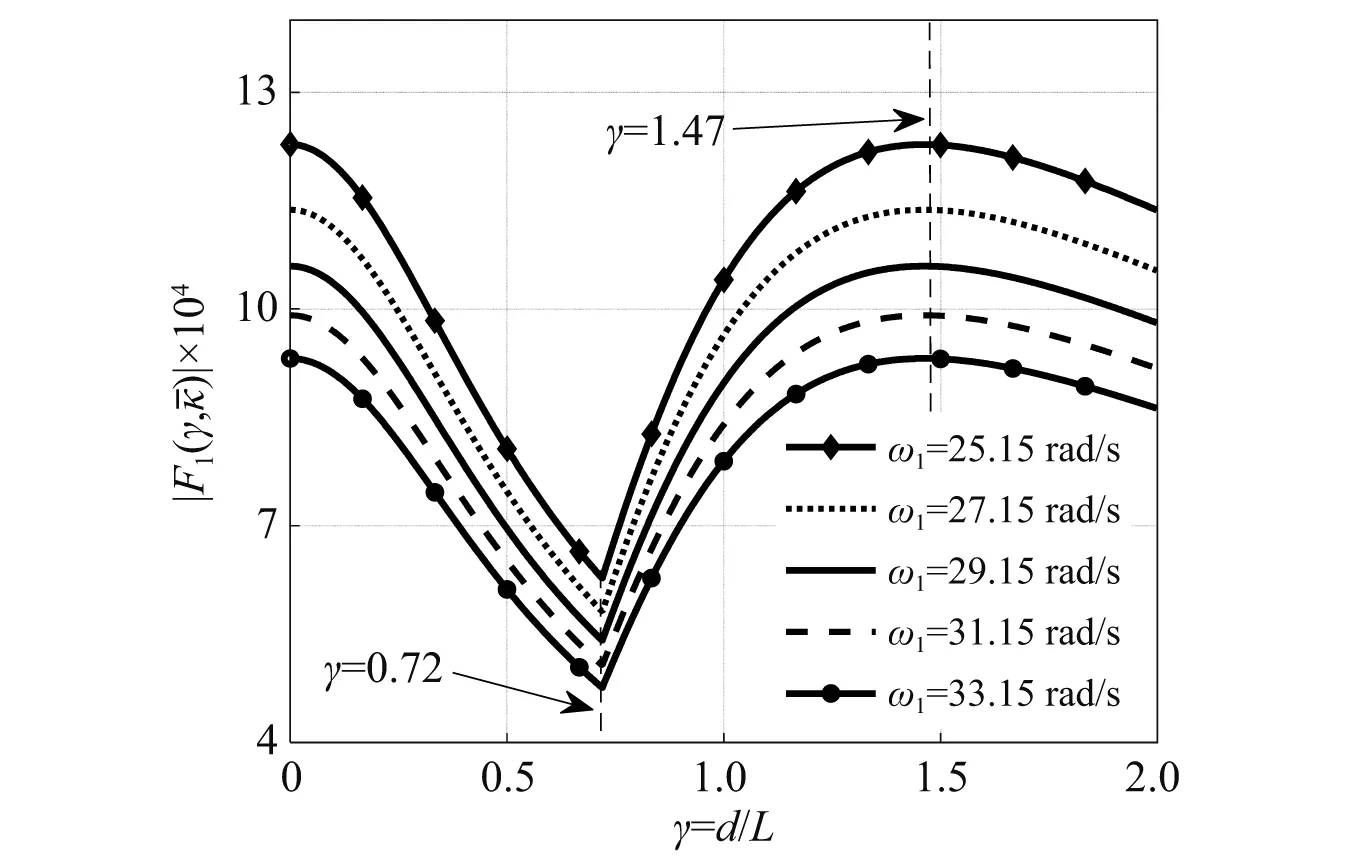
图3 不同轴跨比对应的移动荷载幅值谱最大值
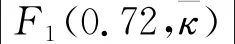
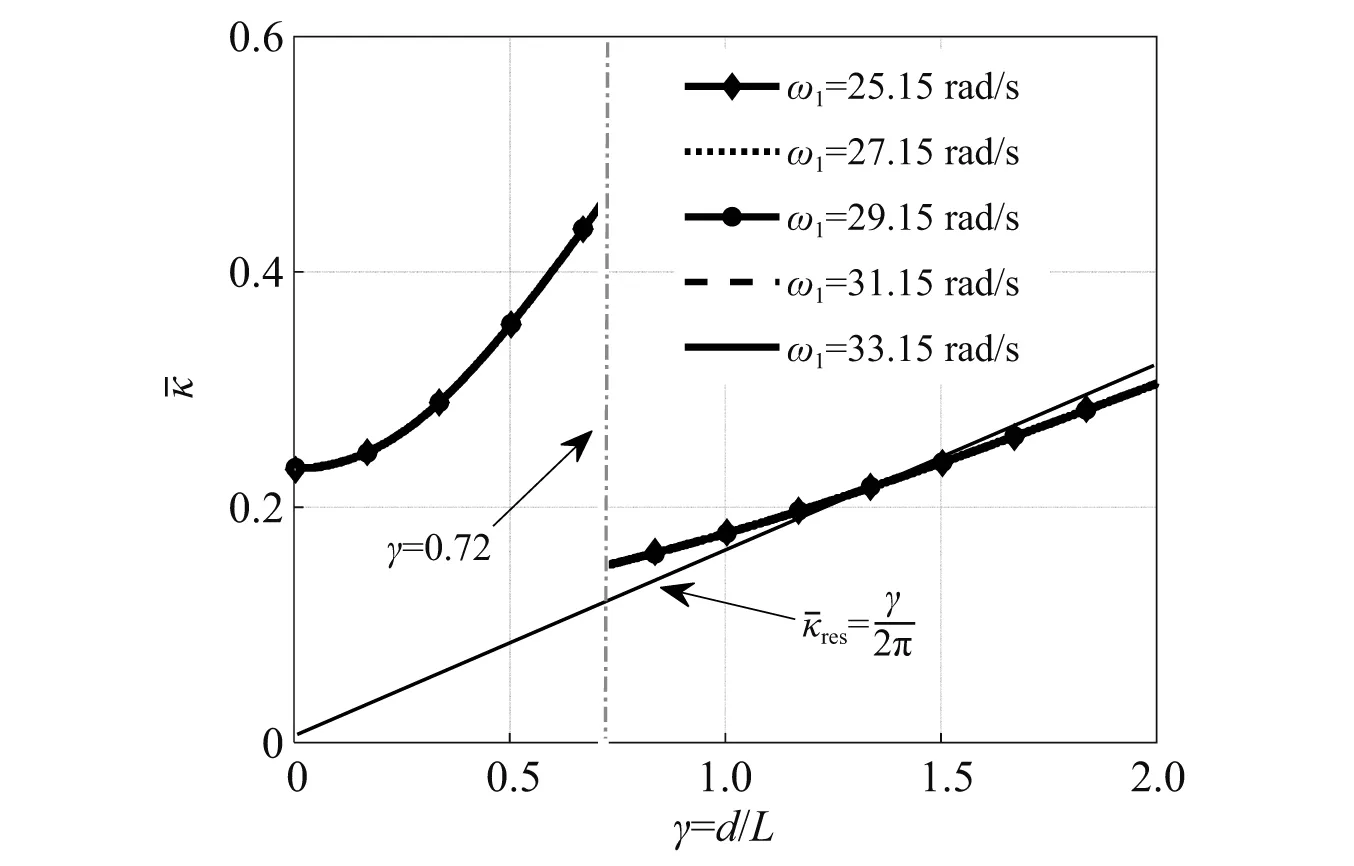
图4 移动荷载幅值谱最大值时的曲线
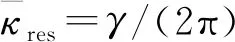
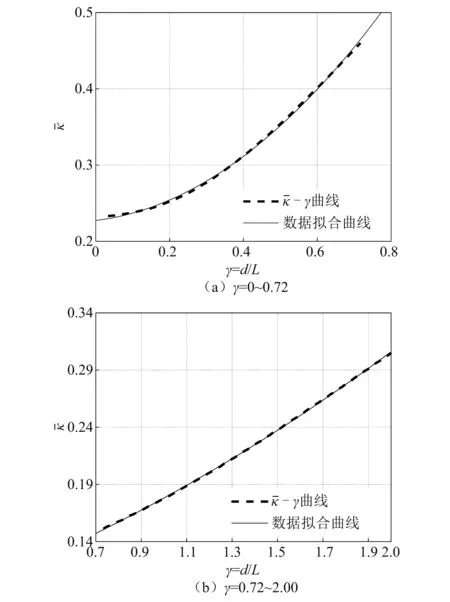
图5 移动荷载幅值谱最大值时的拟合曲线
(13)
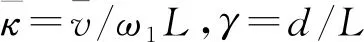
(14)
移动荷载作用在桥梁结构上存在自由振动与受迫振动两部分的响应,如不考虑阻尼的影响,受迫振动的时间要远小于自由振动的时间。而频域分析是对运动方程在整个时域内进行积分,因此对于傅里叶变换得到的移动荷载谱、桥梁位移响应谱,能够有效地反映桥梁结构的自由振动。因此,基于频域分析法得到的式(14)移动荷载速度,将会使得桥梁自由振动产生最大位移响应,该速度仅与桥梁自振频率、跨径,移动荷载轴距有关。下面将采用数值算例,对上述结果进行验证。
3 数值验证分析
首先根据表1中的桥梁与荷载参数,得到不同移动荷载速度下对应的桥梁自由振动幅值与移动荷载幅值谱|F1(ω1)|如图6、图7所示。图6是基于时域方法得到的不同速度下移动荷载引起的桥梁自由振动幅值,该方法需要对运动方程进行反复求解;图7是基于频域分析法得到的不同速度下移动荷载幅值谱|F1(ω1)|。
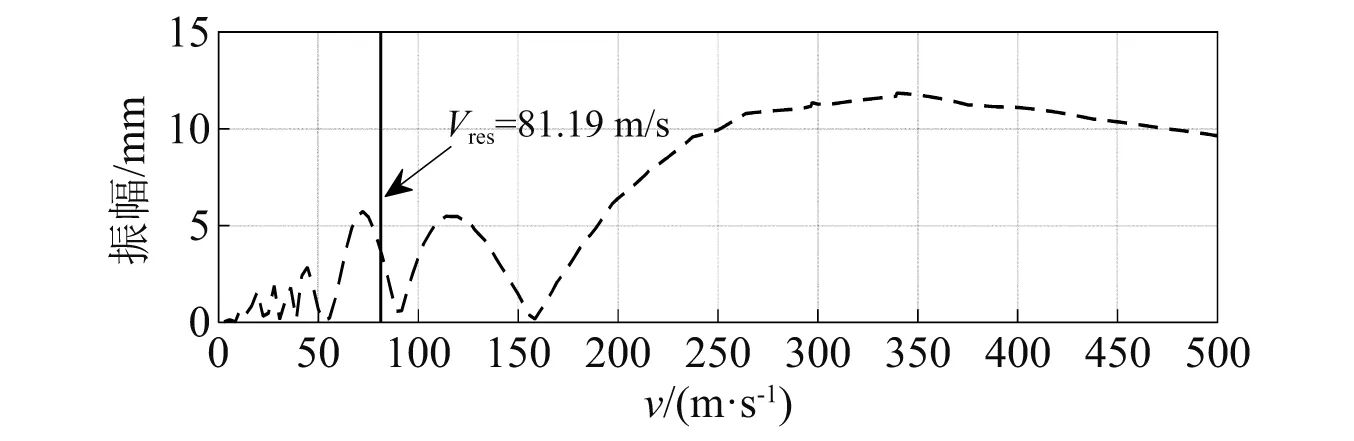
图6 不同时速下桥梁自由振动位移响应幅值
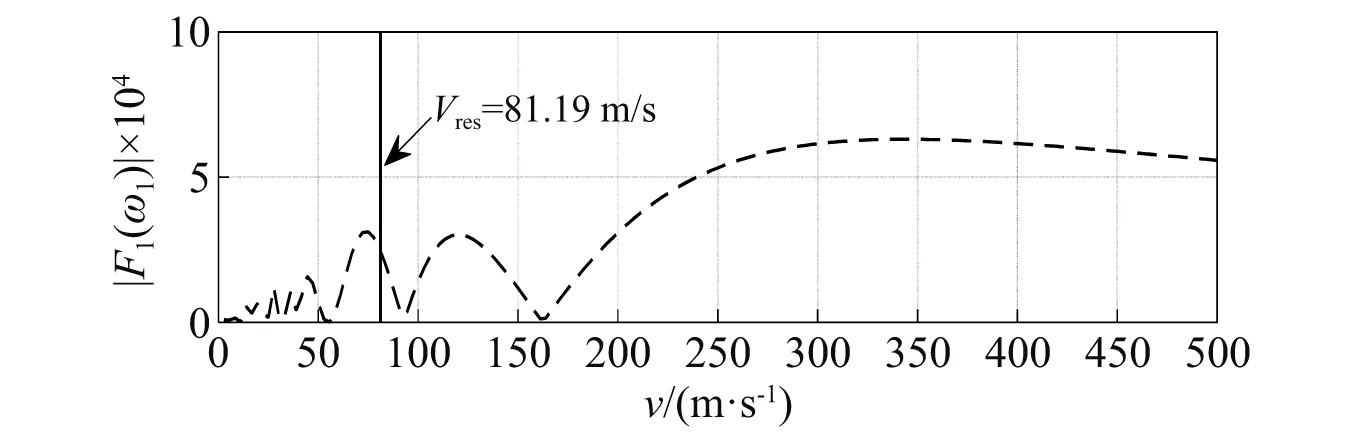
图7 不同时速下移动荷载幅值谱
根据图6可知,移动荷载分别从低速到高速匀速通过桥梁,对于不同的移动荷载速度,桥梁自由振动幅值出现了一系列极值点,其中极大值与极小值交替出现,图7的不同速度下移动荷载幅值谱|F1(ω1)|也具有类似的规律。对比图6、图7可以观察出,桥梁自由振动幅值与移动荷载幅值谱|F1|中各个极值点,所对应的荷载移动速度是相互吻合的,说明了文中频域推导的移动荷载幅值谱|F1(ω1)|能够有效反映出各移动荷载速度下桥梁自由振动位移响应幅值的大小关系。

根据图6、图7可知,对于桥梁自由振动幅值与移动荷载幅值谱|F1(ω1)|各个极值点,其所对应的荷载移动速度是相互吻合的,这说明式(14)用于确定某移动荷载速度下,桥梁自由振动发生最大位移响可行的。为了进一步表明该速度公式的广泛适用性和有效性,下面将采用文献[17]中的另一桥梁及荷载数据(见表2),并考虑不同的移动荷载轴距d,即不同的轴跨比γ,进行分析验证。

表2 另一组桥梁及荷载参数
根据式(14)可知,移动荷载速度公式在γ为0.72处进行了分段。因此,为了验证整个移动荷载速度公式的有效性,对γ分别在0~0.72与0.72~2.00内取值进行分析验证,其取值为0.4,0.72和1.5,即移动荷载轴距分别为8 m,14.4 m和30 m。根据表2的桥梁与荷载参数,不同移动荷载速度下对应的移动荷载幅值谱|F1(ω1)|与桥梁自由振动位移响应幅值如图8、图9所示。
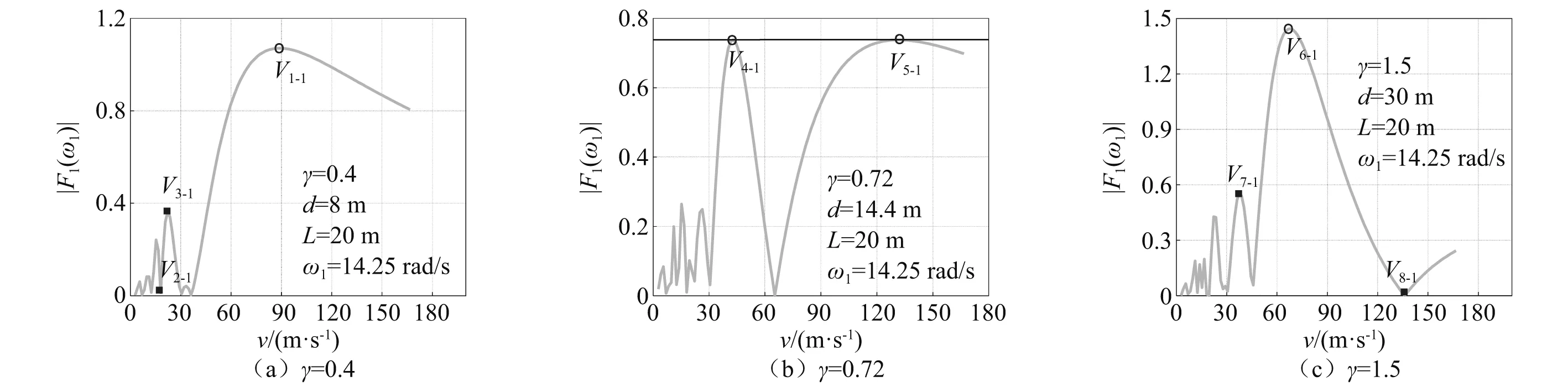
图8 不同轴跨比γ的移动荷载幅值谱
图9 不同轴跨比γ的桥梁自由振动位移响应幅值
对比图8(a)~图8(c)可以发现,对于不同的轴跨比γ,对应的移动荷载幅值谱最大值的大小为max{|F1(ω1)|}γ=0.72 为了进一步验证频域分析的移动荷载速度与时域计算结果相互吻合,分别在图8和图9中任意取极值点对应的移动荷载速度见表3所示。表中V1,V3,V4,V5,V6,V7为时域内桥梁自由振动幅值中极大值对应的移动荷载速度,与之相应的频域内移动荷载幅值谱极大值对应的移动荷载速度分别为V1-1,V3-1,V4-1,V5-1,V6-1,V7-1;而对于时域内桥梁自由振动幅值中极小值对应的移动荷载速度为V2,V8,与之相应的频域内移动荷载幅值谱极小值对应的移动荷载速度分别为V2-1,V8-1。如表3所示,频域内的8个极值点对应的移动荷载速度,与时域内相应极值点对应的速度对比,误差非常小,说明了频域分析移动荷载速度的有效性。 表3 各个极值点对应的移动荷载速度 当移动荷载分别以时域内8个极值点对应的速度移动,桥梁跨中位移时程曲线如图10所示。根据图10(a)可知,移动荷载以速度V1,V2,V3通过桥梁,引起桥梁自由振动幅值的大小关系为:max{|y1|max}V2 图10 考虑不同轴跨比γ的跨中竖向位移时程曲线 如图10所示,当移动荷载以V2,V8速度行驶出桥后,桥梁自由振动,几乎处于静止状态,但当移动荷载以V1,V4,V5,V6速度行驶时,桥梁自由振动将发生最大振幅的位移响应。因此,为了避免桥梁自由振动发生最大振幅的位移响应,快速有效确定相应移动荷载速度非常有必要。 对于傅里叶变换得到的移动荷载谱、桥梁位移响应谱,能够有效反映移动荷载作用下桥梁自由振动响应,其中移动荷载幅值谱与时域角度得到的桥梁自由振动响应幅值规律一致。 当轴跨比γ为0,0.72,1.47时,移动荷载幅值谱最大值曲线存在极值;其中在轴跨比γ为0.72时,对应的移动荷载幅值谱最大值最小;而在轴跨比γ为0与1.47时,对应的移动荷载幅值谱最大值相同,均为最大。 两轴集中力移动荷载以文中速度式(14)得到的速度通过桥梁后,会引起桥梁自由振动产生最大位移响应,该速度不仅与桥梁自振频率有关,还与轴跨比γ有关。 移动荷载以共振速度Vres=(ω1d)/(2π)匀速通过梁桥后,引起桥梁的受迫与自由振动响应均不是最大响应,甚至不是极值响应,仅当轴跨比γ在1.5左右时,共振速度Vres才能使得桥梁自由振动位移响应近似达到最大值。这是因为对于其他轴跨比γ,共振速度作用在桥梁上的有限时间内,未能激励起桥梁最大响应。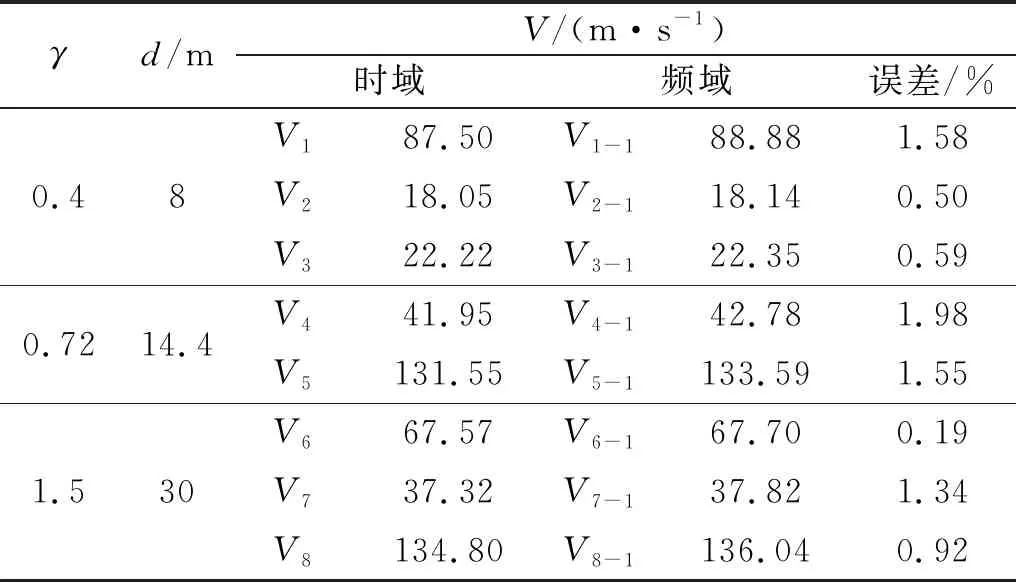

4 结 论


