电动汽车-路面系统机电耦合建模及非线性振动分析

冯桂珍， 李韶华， 赵文忠

(1. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043；2. 石家庄铁道大学 交通运输学院，石家庄 050043； 3. 石家庄铁道大学 机械工程学院，石家庄 050043； 4. 河北交通投资集团公司，石家庄 050091)

轮毂电机独立驱动电动汽车由于传动效率高、机动性和灵活性高、易于实现各种智能控制等优点，得到了极大关注[1-2]。但是，独立驱动电动汽车的动力学与控制面临诸多新的问题和挑战。簧下质量大，导致轮胎动载荷增加，与路面的动力学相互作用更为突出。同时，电机电磁力与转矩波动会对车轮造成电机激励，进一步加剧车轮振动，进而影响轮胎接地安全性、车辆平顺性和稳定性。

目前，关于独立驱动电动汽车的机电耦合振动方面，Wang等[3]研究表明，开关磁阻电机垂向电磁力作用在车轮上，导致轮胎负载显著变化，且频率覆盖宽，涉及车体和车轮部分的共振频率。Tan等[4]指出，路面激励通过轮辋传递到驱动电机，导致电机定转子气隙变化，产生电磁力不平衡，影响车辆动力学特性。Wang等[5]建立了通用的直流电机模型，通过硬件在环实验验证了控制方法，并应用于智能车辆的主动转向控制中。李哲等[6]建立了考虑电机激励不平衡径向力的悬架系统机电耦合模型，提出了电磁主动悬架多目标粒子群优化设计方法，抑制轮毂电机驱动电动汽车的振动负效应问题。林程等[7]选用黏性联轴器作为机电耦合装置提高了独立驱动汽车的动力性和操纵稳定性，并起到辅助防滑的作用。张利鹏等[8]通过轮毂电机的力矩主动分配实现了电动汽车的侧倾稳定性控制，提出的横摆和侧倾运动联合解耦控制方法，可有效控制侧倾运动，大幅度提高整车稳定性。史晓燕等[9]针对轮毂电机垂向振动问题，提出了一种新型动力吸振构型和半主动悬架混合控制策略。曹占勇等[10]针对电动汽车由于传动系低阻尼特性产生的转矩波动问题，提出了模糊自整定PID(proportional integral differential)控制器和神经网络PID控制器，提高电机控制器的响应速度和抗干扰能力。左曙光等[11]采用有限元方法构建了一套虚拟电动振动系统，该系统空间上非均匀分布，相对于线性电磁模型，提供了更真实的振动环境。上述文献主要分析了电机激励对车辆的影响，但未考虑车路相互作用，没有对道路进行建模，也没有考虑路面二次激励的影响。

关于车路相互作用方面，Zhang等[12]提出非线性多弹簧线接触轮胎力模型，考虑路面不平顺和车轮跳离路面，便于车桥耦合动力学分析。李金辉等[13]建立了三轴重型汽车，分析非平稳行驶条件下重型汽车轮胎附加动载特性，并与匀速平稳行驶工况进行对比。Yang等[14-15]建立了车路耦合动力学模型，认为路面振动会给汽车带来二次激励，并影响轮胎动载和附着特性，提出了改进的轮胎滚子接触力学模型。上述文献主要针对传统汽车与路面的相互作用，没有研究电动汽车，未涉及电机激励对车辆响应的影响。

独立驱动电动汽车因簧下质量增加导致车轮振动剧烈，与路面的动力学相互作用更加突出。但现有研究主要针对传统汽车，关于电动车轮与路面动力学相互作用的研究尚不多见，且以2自由度1/4悬架模型居多。而考虑悬架刚度、阻尼和轮胎刚度非线性，研究独立驱动电动汽车在路面不平顺、电机激励及车路耦合激励的综合作用下的机电耦合动力学，尚未见文献报道。鉴于此，论文建立了轮毂电机电动汽车-路面系统机电耦合动力学模型，研究了电动汽车的振动响应受路面不平顺、电机激励和路面二次激励综合作用的影响规律，以车速及非线性参数对汽车响应的影响。

1 电动汽车-路面系统机电耦合模型

1.1 系统运动微分方程

假设路面对电动汽车左右轮的激励相同，汽车结构对称，建立轮毂电机驱动电动汽车5自由度半车模型，且轮胎刚度、悬架刚度、悬架阻尼都为非线性，用两端简支的有限长Bernoulli-Euler梁模拟柔性公路路面，用Kelvin黏弹性地基模拟公路路基，并假定t=0时刻汽车位于梁中点，以速度v沿直线匀速行驶，分析汽车纵向铅垂平面内的振动问题，如图1所示。

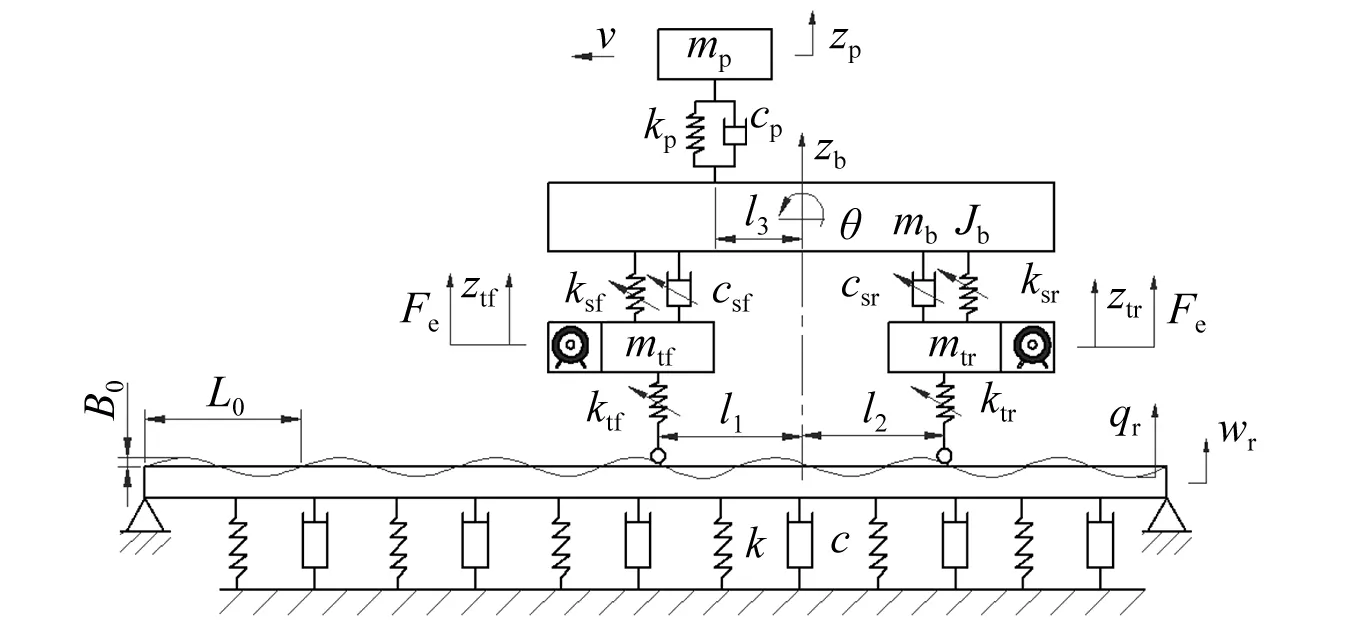
图1 电动汽车-路面系统机电耦合模型

假设车体俯仰角θ变化范围很小，根据达朗贝尔原理及振动理论，建立电动汽车及路面垂向振动微分方程[16]

(1)

(2)

式中：zb为车体质心处垂向位移；θ为车体俯仰角；ztf，ztr为前、后非簧载质量垂向位移；zp为座椅垂向位移；mb，Jb为车体质量及绕质心的转动惯量；mtf，mtr为前、后非簧载(包含电机)质量；mp为座椅(包括驾驶员)质量；ktf，ktr为前、后轮胎刚度；ksf，ksr为前、后悬架刚度；kp为座椅刚度；csf，csr为前、后悬架阻尼系数；cp为座椅阻尼系数；Fe为电机垂向激励合力；l1，l2，l3分别为前、后轴、座椅至车体质心距离；E为材料弹性模量；I为截面对中性轴的惯性矩；ρA为单位长度路面的质量(ρ为路面的密度，A为路面的横截面积)；k为路基反应模量；c为路基阻尼系数；Ftf，Ftr为考虑车路耦合作用的前、后轮胎力； δ为狄拉克函数；x为汽车行驶方向的位移；wr为路面的垂向振动位移；wt为车路耦合振动引起的路面二次位移激励。

路面不平顺采用正弦激励，表达式为

(3)

式中：Ω为路面激励频率；B0，L0分别为路面不平顺幅值及波长。

轮胎力为

(4)

式中，Gf，Gr为前、后轴轮胎静载，其表达式分别为

非线性悬架刚度采用三次多项式，非线性轮胎刚度采用二次多项式，悬架阻尼采用非线性液压阻尼，表达式分别如下：

非线性前、后悬架刚度

(5)

非线性前、后轮胎刚度为

(6)

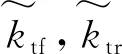
悬架阻尼采用非线性液压阻尼，其表达式为非线性悬架阻尼为

(7)

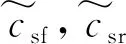
1.2 电机垂向激励

据文献[17]，采用开关磁阻电机，电机垂向激励合力的解析表达式为

(8)

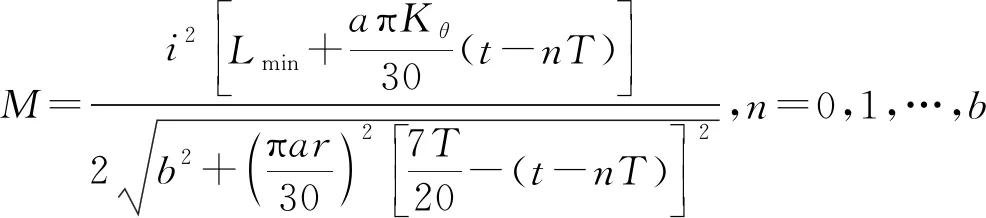
1.3 路面二次激励

根据模态叠加原理，式(2)中路面垂向位移可展开为无穷级数

(9)

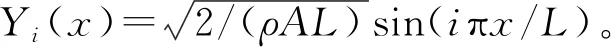
将式(9)代入式(2)，两边同时乘以Yj(x)并沿地基梁长L对x积分，根据模态振型的正交性，可得

(10)

其中，

(11)

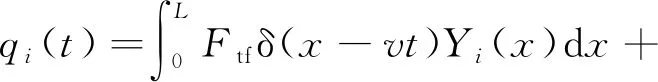
(12)

由式(10)求出ηi(t)，代入式(9)，即可求出路面垂向位移响应wr(x,t)的解析表达式

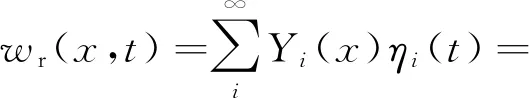
(13)

将x=L/2+vt代入式(13)，即可得到汽车从梁中点开始行驶时，轮胎下方每个时刻的路面振动位移，本文将之称为路面二次激励，其表达式为

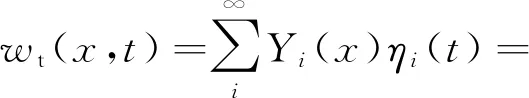
(14)

将路面二次激励wt(x,t)代入式(4)，即可求得考虑车路耦合作用的轮胎力Ftf，Ftr。

2 电动汽车-路面系统非线性振动分析

综合考虑路面不平顺、路面二次激励和电机激励作用时，机电耦合模型的系统运动微分方程组具有高维、参数时变、车路机电耦合等特性，解析解难以求解，本文通过四阶龙格库塔数值方法，利用MATLAB软件编程求解三重耦合激励下的汽车和路面响应。

选取汽车参数如下[18]：mp=100 kg,mb=1 740 kg,Jb=2 424.9 kg·m2,mtf=103.5 kg,mtr=120 kg;kp=1 800 N/m,ksf=114 000 N/m,ksr=160 400 N/m,ktf=310 240 N/m,ktr=324 600 N/m,csf=2 600 N·s/m，csr=6 500 N·s/m，cp=194 N·s/m，β1=0.01,β2=0.1,β3=0.6,β4=1/3,l1=1.666 m,l2=0.934 m，l3=1.816 m;v=60 km/h。

选取路面和路基模型系统参数：E=1.6×109N/m2，k=48×106N/m2,c=0.3×105N·s/m2，路面为宽度b=6 m、厚度h=0.01 m、矩形截面，长度L=140 m；沥青混合料密度ρ=2.5×103kg/m3；路面不平顺参数：L0=10 m，B0=0.010 m。

2.1 路面模态叠加阶数的选取

为了保证计算结果的正确性，对路面模态叠加阶数的选取进行了数值试验。取模态叠加阶数NM=1～200，计算模态叠加阶数对路面响应和车辆响应幅值的影响，如图2和图3所示。

图2 模态叠加阶数对路面响应幅值的影响

图3 模态叠加阶数对车辆响应幅值的影响

由图2和图3可知，模态叠加阶数NM在30阶以下，对路面响应及路面二次激励响应较大，30阶以上影响较小。此外，由式(11)可求得两端简支的黏弹性地基梁的模态频率，且前200阶频率都小于80 Hz。文献[19]规定，人体承受的周期振动和非周期振动的频率范围在1～80 Hz。鉴于以上分析，模态截断阶数NM取200。

2.2 路面二次激励的影响

分别取路面不平顺幅值B0=0.010 m和B0=0.001 m，计算得到车路耦合情况下，路面二次激励对车辆响应的影响。限于篇幅，只列出B0=0.001 m时座椅加速度、车体加速度、俯仰角加速度、前、后悬架动挠度和前、后轮动载荷的影响，如图4所示。表1为B0=0.010 m和B0=0.001 m时车辆响应最大幅值及相对差别。

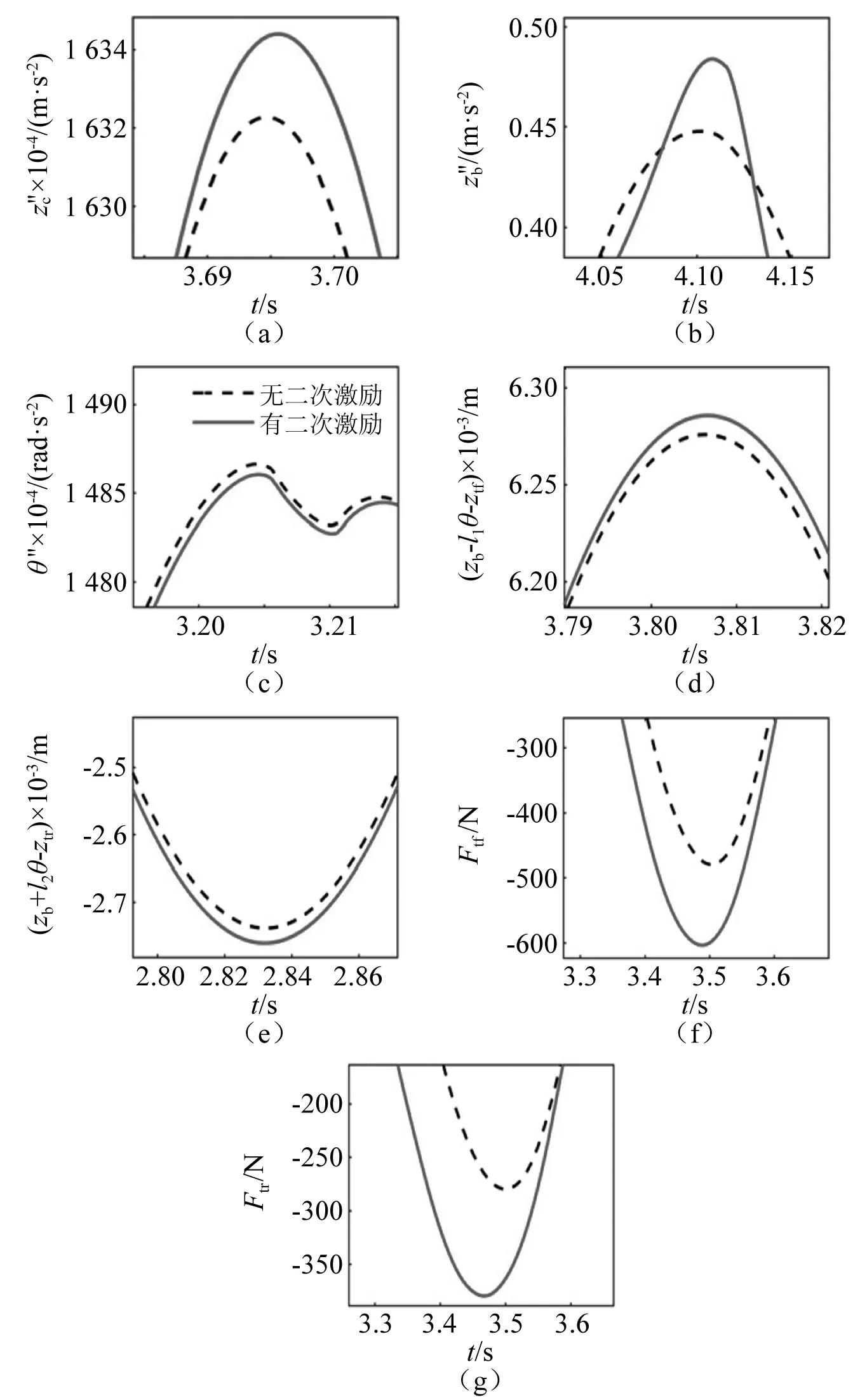
图4 路面二次激励对车辆响应的影响(B0=0.001 m)

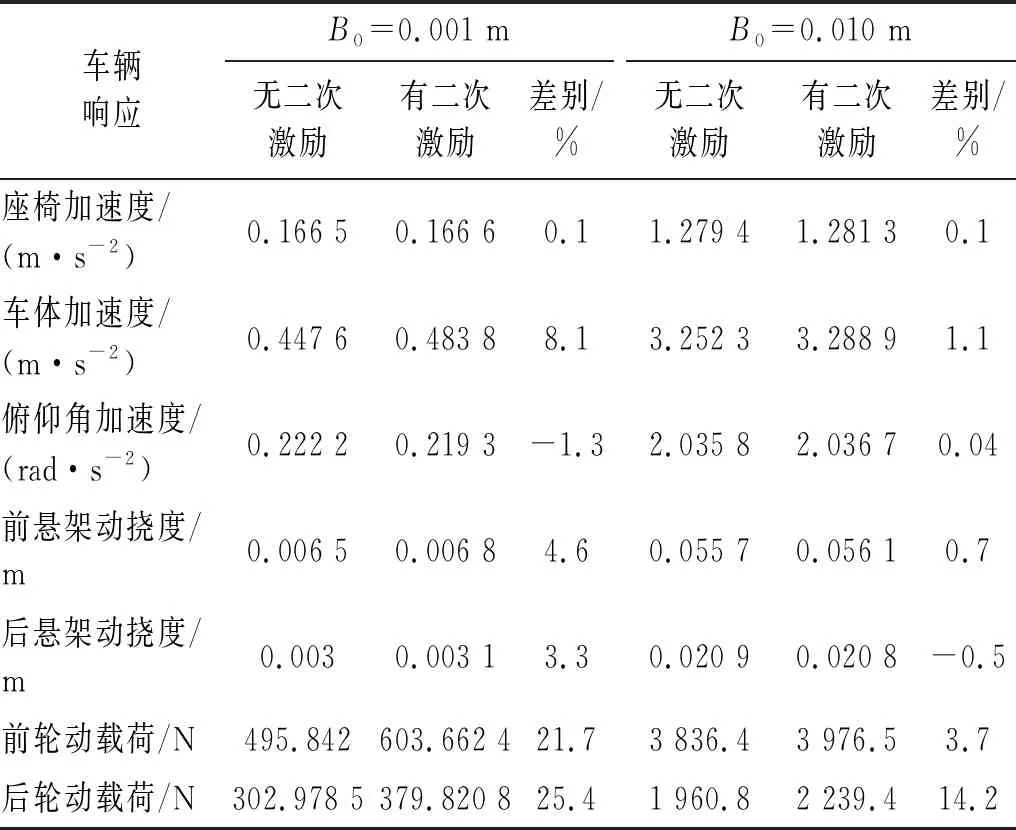
表1 路面二次激励对车辆响应幅值的影响

由图4及表1可知：①路面二次激励对轮胎动载荷的影响最大，车体加速度和悬架动挠度的影响次之，对座椅加速度和俯仰角加速度的影响较小；②路面不平顺幅值越小，路面二次激励对车辆响应的影响越大，其中B0=0.010 m和B0=0.001 m时，前轮动载荷最大增幅分别3.7%和21.7%，后轮动载荷最大增幅分别为14.2%和25.4%。可见，在平坦路面上行驶，路面二次激励对车辆响应的影响不容忽视。

2.3 电机激励的影响

激励形式分别为：①考虑路面不平顺和路面二次激励的二重激励；②考虑路面不平顺、路面二次激励和电机激励的三重激励。将路面不平顺qr、路面二次激励wt、电机垂向激励合力Fe分别代入式(1)、式(2)和式(4)，通过四阶龙格库塔法可求得非线性电动汽车在综合激励作用下的响应。车辆以60 km/h匀速行驶，座椅加速度、车体加速度、俯仰角加速度、前、后悬架动挠度和前、后轮动载荷受激励形式的影响曲线，如图5所示。激励形式对车辆响应最大幅值的影响及相对差别，如表2所示。

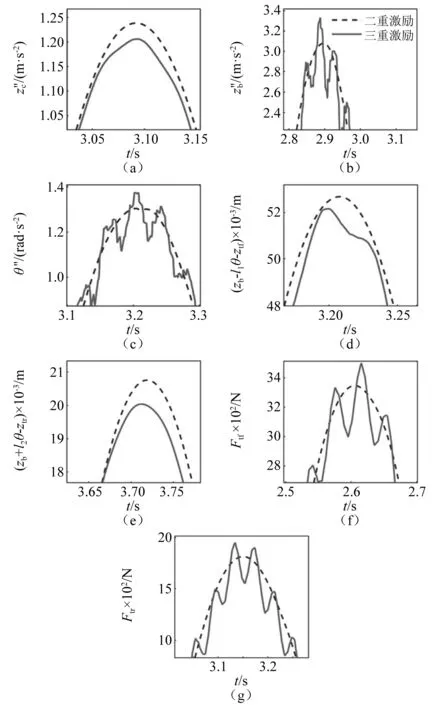
图5 电机激励对车辆响应的影响

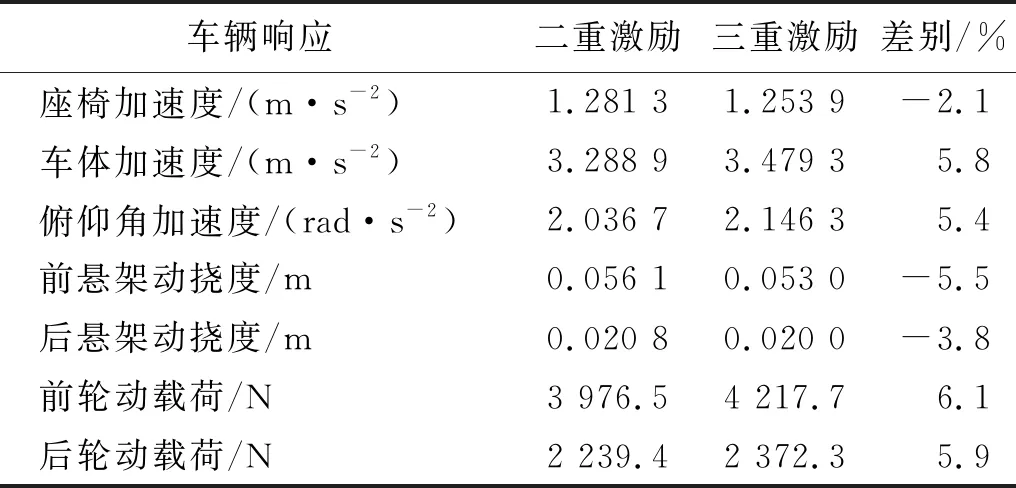
表2 电机激励对车辆响应最大幅值的影响

由图5及表2可知：考虑电机激励后，对轮胎动载荷和车体加速度的影响最大，最大幅值分别增加6.1%和5.8%，悬架动挠度和俯仰角加速度的影响次之，座椅加速度的影响较小。且悬架动挠度和座椅加速度的增大幅值都为负值，说明非线性悬架和阻尼对电机激励产生的垂向振动具有一定的隔振效果，降低了座椅加速度和悬架动挠度。

2.4 行驶速度的影响

车辆行驶速度从5～100 km/h，增量为5 km/h，对车辆响应最大幅值的影响，如图6所示。

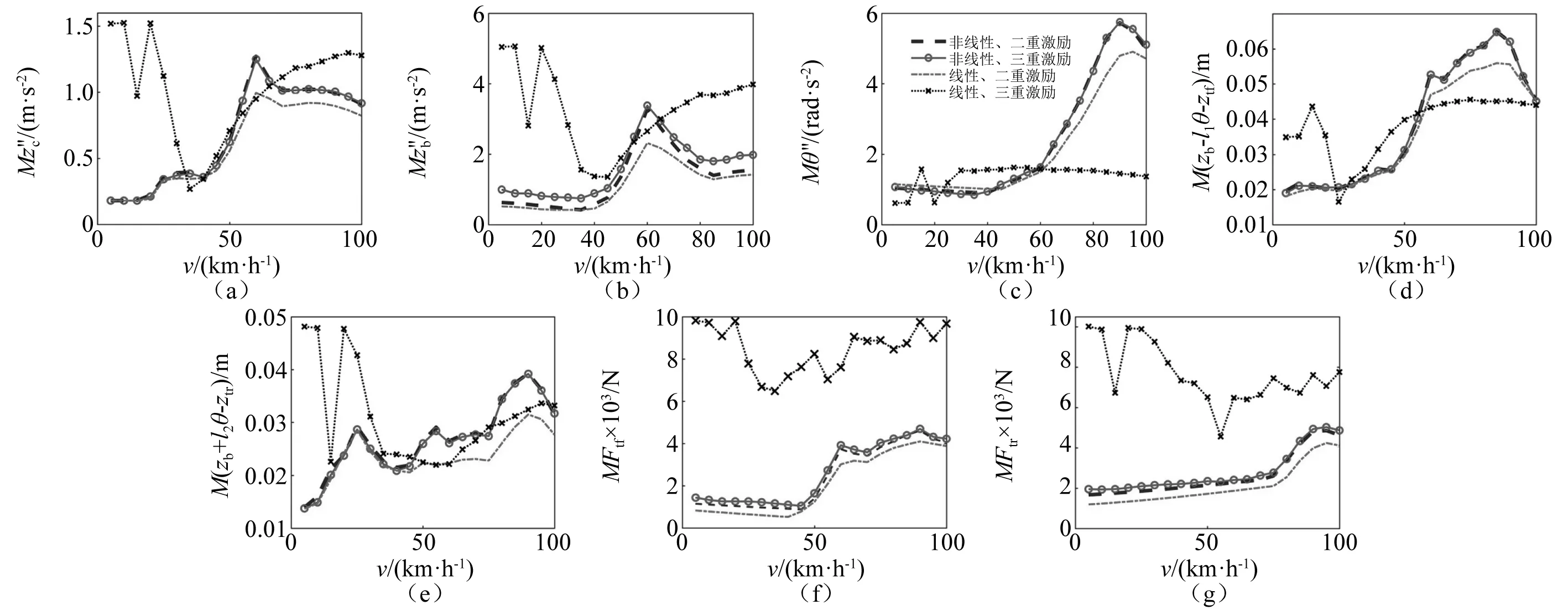
图6 速度对车辆响应最大幅值的影响

由图6可知：

(1) 随着行驶速度的增加，非线性模型的车辆响应幅值整体呈现增加趋势。其中，座椅加速度最大幅值在25 km/h和60 km/h处出现两个峰值，车体加速度最大幅值在60 km/h处出现一个峰值，俯仰角加速度在90 km/h处出现一个峰值，主要原因是由于座椅和车体的垂直振动及车体俯仰振动的固有频率分别为0.67 Hz，1.66 Hz，2.42 Hz，当车辆25 km/h，60 km/h和90 km/h行驶时，路面激励频率(Ω=2πv/L0)分别为0.69 Hz，1.67 Hz，2.5 Hz，发生共振所致。同时，共振导致悬架动挠度和轮胎力也出现了峰值。

(2) 不同行驶速度时，考虑电机激励的三重激励相比于不考虑电机激励，后轮动载荷最大幅值的影响最大，最大幅值增加3.5%；车身加速度的影响次之，最大增幅2.9%；座椅加速度和悬架动挠度最大幅值增加都为负值，其中座椅加速度最大幅值减小1.7%，说明非线性悬架和阻尼对电机激励产生的垂向振动具有一定的隔振效果。

(3) 非线性模型在考虑与不考虑电机激励作用下，行驶速度对车辆响应的影响与线性模型在不考虑电机激励的变化趋势基本一致，但考虑电机激励时，线性模型受速度影响波动较大。说明考虑电机激励时，非线性模型较线性模型更为稳定。

2.5 车辆非线性的影响

为了进一步研究非线性刚度和阻尼系数对车辆响应的影响，在二重激励和三重激励下，分别改变参数β1，β2，β3，β4中的一个，固定基本参数不变，得到车辆响应的最大幅值影响曲线，如图7～图10所示。非线性参数对车辆响应最大幅值影响的差别，如表3所示。

由图7～图10及表3可知：

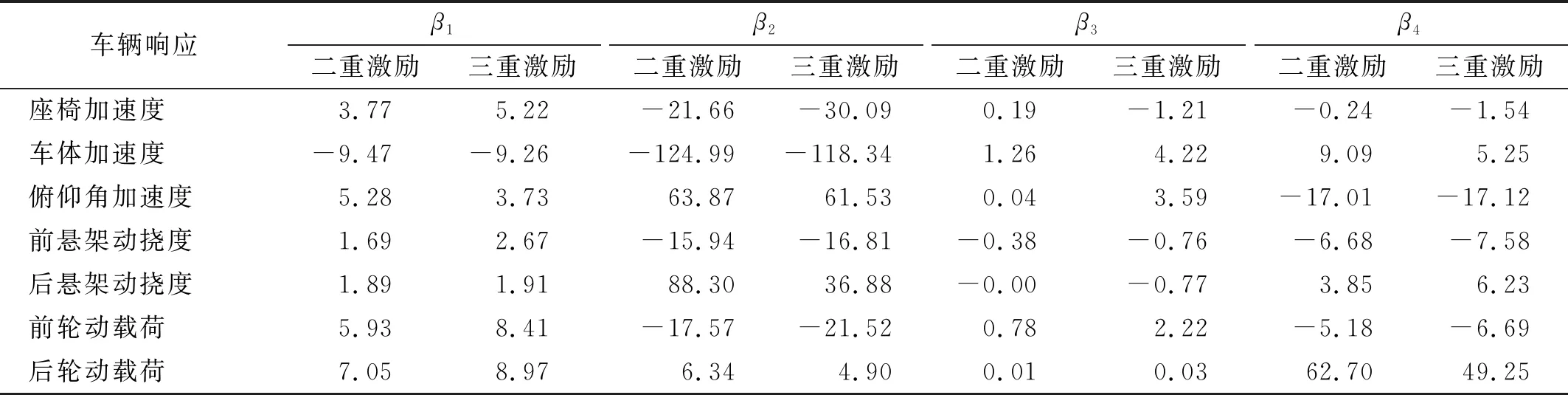
表3 非线性参数对车辆响应最大幅值影响的差别

图7 β1对车辆响应最大幅值的影响

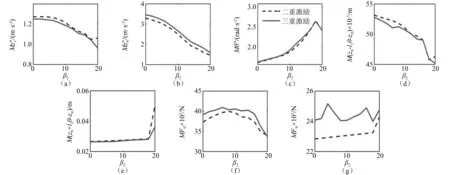
图8 β2对车辆响应最大幅值的影响

图9 β3对车辆响应最大幅值的影响

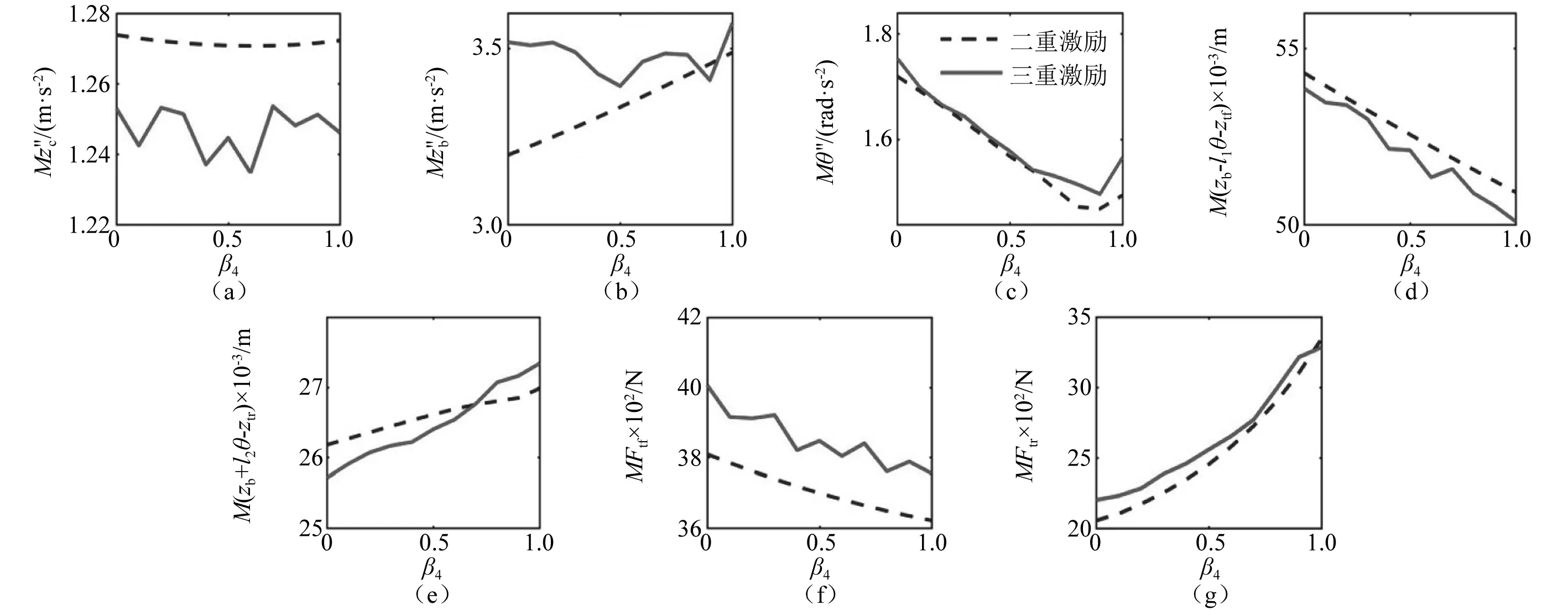
图10 β4对车辆响应最大幅值的影响

(1) 轮胎非线性刚度系数β1增大，车体加速度降低，最大幅值降低9.26%(考虑电机激励)、9.47%(不考虑电机激励)；但同时使座椅加速度、前、后悬架动挠度和前、后轮动载荷及俯仰角加速度都增加，其中，轮胎动载荷的增幅最大，考虑电机激励超过8%，不考虑电机激励超过5%，悬架动挠度的影响最小，增幅在2%左右。

(2) 悬架刚度平方非线性系数β2增大，座椅加速度、车体加速度和前悬架动挠度都降低，其中，车体加速度的降幅最大，考虑电机激励降低118.34%，不考虑电机激励降低124.99%，座椅加速度的降幅次之，降幅超过21%；俯仰角加速度、后悬架动挠度和后轮动载荷都增大，其中，俯仰角加速度的增幅最大，超过60%，后轮动载荷的影响最小，前轮动载荷在β2<10时缓慢增加，在β2>10时降低，但在β2>18时，后悬架动挠度、俯仰角加速度和后轮动载荷都出现突变，其中，后悬架动挠度的突变最为显著，不容忽视。

(3) 悬架刚度立方非线性系数β3增大，对汽车响应的影响较小，其中，后轮胎轮载荷、前、后悬架动挠度都小于1%。

(4) 悬架阻尼不对称系数β4增大，车体加速度、后悬架动挠度和后轮动载荷都增加，其中，后轮动载荷的影响最大，最大增幅49.25%(考虑电机激励)、62.7%(不考虑电机激励)，车体加速度和后悬架动挠度的最大增幅都小于15%；前悬架动挠度、前轮动载荷和俯仰角加速度都有所降低，其中，俯仰角加速度的降幅最大，超过17%，前悬架动挠度和前轮胎的降幅都超过5%；座椅加速度的影响最小。

综合上述分析可知，考虑电机激励、路面二次位移激励和路面不平顺的三重综合激励，非线性刚度和阻尼系数的影响曲线出现波动，但总体趋势与不考虑电机激励的影响基本一致。其中，从提高汽车平顺性角度看，提高悬架刚度平方非线性系数β2最为有利，增大β2可显著降低车体加速度(降幅超过100%)，同时使座椅加速度、前悬架动挠度和前轮动载荷降低，但在β2>18时，后悬架动挠度出现突变，应引起重视；其次是悬架阻尼不对称系数β4，增大β4可降低俯仰角加速度(超过17%)，同时降低前悬架动挠度和前轮动载荷，但β4的增大也使后轮动载荷增大(超过49%)，应综合考虑；增大轮胎非线性刚度系数β1，可降低车体加速度，但车辆的其他指标都增加，其中前、后轮动载荷增加较为显著，影响车辆行驶安全性，设计中不容忽视；悬架刚度立方非线性系数β3对汽车响应的影响最小。因此，实际车辆设计可以通过调节各参数，达到提高乘坐舒适性和行驶安全性的目的。

3 结 论

建立了非线性电动汽车-路面系统机电耦合动力学模型，推导了简支边界条件下路面垂向振动引起的二次激励，并分析了车辆响应受路面二次激励、电机激励、车速和悬架非线性的影响规律。研究表明：

(1) 在路面不平顺、电机激励和路面二次激励三重综合激励作用下，非线性模型对汽车响应的性能指标明显优于线性模型，尤其是轮胎动载荷，非线性模型的前、后轮动载荷最大幅值比线性模型降低86.4%和181.2%，说明非线性汽车模型在一定程度上降低了电机激励产生的轮胎动载荷。在汽车系统非线性参数中，悬架刚度平方非线性系数对汽车响应的影响最大，悬架阻尼不对称系数和轮胎非线性刚度系数的影响次之，悬架刚度立方非线性系数的影响最小。因此，为了更准确、合理地计算电动汽车响应，应采用非线性车辆模型进行研究。

(2) 非线性模型在考虑电机激励和不考虑电机激励作用下，行驶速度对车辆响应的影响与线性模型在不考虑电机激励的变化趋势基本一致，但考虑电机激励时，线性模型受速度影响波动较大，说明考虑电机激励时，非线性模型较线性模型更为稳定。随着车速的增加，非线性模型的车辆响应幅值整体呈现增加趋势，且以25 km/h，60 km/h和90 km/h行驶时，激励频率分别接近座椅和车体的垂向振动及俯仰振动的固有频率，发生共振，导致车辆响应增大，因此，车辆行驶过程中应尽量避开共振区。

(3) 路面二次激励对轮胎动载荷的影响最大，悬架动挠度和车体加速度的影响次之，对座椅加速度和俯仰角加速度的影响较小。路面不平顺幅值越小，路面二次激励对车辆响应的影响越大，可见，在平坦路面上行驶，路面二次激励对车辆响应的影响不容忽视。

(4) 电机激励对非线性汽车模型的轮胎动载荷和车体加速度影响最大，俯仰角加速度和悬架动挠度的影响次之，座椅加速度的影响较小。轮胎动载荷增加，会影响汽车的接地安全性和行驶稳定性。因此，电机激励对电动汽车响应的影响应予以重视。