融合注意力机制的改进DBN变工况齿轮箱故障诊断方法

张智禹， 尹爱军， 谭 建

(1. 重庆大学 机械工程学院 机械传动国家重点实验室，重庆 400044;2. 中国石油西南油气田分公司重庆气矿，重庆 400021)

齿轮箱作为机械传动系统中关键组件，由于其结构复杂、工况环境多变等因素导致其经常出现故障，因此齿轮箱故障诊断方法研究引起广泛关注[1]。而在变工况条件下，同类故障间的振动幅值、能量存在较大差异使得齿轮箱故障诊断更加困难，经常出现误诊和漏诊问题[2]。因此，提出一种针对变工况下齿轮箱故障诊断方法十分必要。

近年来，基于深度学习的故障诊断算法快速发展， Liu等[3]直接使用长短期记忆神经网络对时域信号进行特征提取，用于诊断旋转机械故障。张小强等[4]利用时域与频域特征结合进行行星齿轮磨损和断齿的检测。Chen等[5]提出结合时频域信号处理方法离散小波变换与卷积神经网络用于行星齿轮箱故障诊断。然而时域、频域特征由于对非平稳信号不敏感[6]、特征性能不稳定[7]等原因单独作为齿轮箱故障诊断特征参数不适用，时频域特征受Heisenberg测不准原理对非平稳信号分析存在局限[8]。因此，为了获得齿轮箱全面的、多维度的信息，本文提取振动信号的时域、频域、小波包时频域特征形成高维特征集。

在获得全面的特征集合后，如何挖掘内在信息从而精确识别变工况条件下齿轮箱故障是至关重要。部分学者通过增加深度学习模型层数，通过大规模参数训练来学习齿轮箱故障特征[9-10]，由此带来网络模型训练时间长、收敛困难等问题[11]。针对这些问题，本文利用深度置信网络(deep belief networks, DBN)具有的贪心学习优势，分别对三个维度特征进行深度挖掘；同时为解决多个网络输出间串行连接无权重分配机制问题[12]，结合注意力机制，对变工况齿轮箱状态特征自适应 “注意”。最后改进DBN中Softmax损失函数为余弦损失函数，将损失从欧几里德空间映射到角空间从而降低对变工况引起的信号强度的敏感性。

本文提出了融合注意力机制的改进DBN变工况齿轮箱故障诊断方法，为解决单一故障特征诊断准确性低的问题，提出融合时域、频域、小波包时频域特征作为故障诊断参数。使用余弦损失函数改进后的DBN网络结合注意力机制解决变工况敏感性问题及网络输出动态加权问题。试验表明，该方法在变工况齿轮箱故障诊断中具有较好的效果。

1 融合注意力机制的改进DBN模型

1.1 深度置信网络

DBN是由多个受限玻尔兹曼机(restricted Boltzmann machines, RBM)栈式叠加而成[13]。其中RBM可视为一个无向图模型，是一种基于能量函数的概率建模方法。如图1所示，RBM包含一个可见层v=(v1,v2,…,vn)与一个隐藏层h=(h1,h2,…,hm)，层间通过权重矩阵Wn×m实现双向全连接，层内单元无连接。

图1 RBM结构

对于一组给定的状态(v,h)，其能量函数定义为

(1)

式中：wij为可见单元vi与隐藏单元hj间的连接权重；bi为可见层中第i个神经元的偏置；cj为隐藏层中第j个神经元的偏置。

基于能量函数得到任一组(v,h)的联合概率分布为

(2)

当给定各可见层单元状态v，可得隐藏层单元的激活概率为

(3)

相应的给定隐藏单元状态h，可得可见层单元激活概率为

(4)

式中，S函数为Sigmoid函数，定义为

S(x)=1/(1+e-x)

(5)

为训练RBM，通过最大化训练集上的对数似然来调整参数，对于连接权重wij，其偏导为

(6)

式中， 〈vihj〉d，〈vihj〉m分别为数据分布与模型分布的期望。由于〈vihj〉m计算复杂度高，因此采用对比散度(contrastive divergence, CD)方法[14]进行梯度估计。因此权重参数wij可以通过式(7)进行更新。

Vwij=η(〈vihj〉d-〈vihj〉r)

(7)

式中： 〈vihj〉r为可见层重构的分布期望；η为学习率； 相应的bi,cj偏置参数可通过相同方法进行更新。

利用RBM结构拥有的无监督贪婪学习优势及数据特征凸显能力分别对时域、频域、小波包特征进行挖掘，学习其中对齿轮箱故障有效的深度特征。

1.2 注意力DBN模型

在1.1节获得多个维度的深度特征后，需要结合这些特征以获得更全面的故障信息，目前部分学者在结合多网络输出、多域特征时常采用串行连接方式，如图2所示，此方式明显忽略了不同特征对故障诊断结果贡献度大小不同的因素。

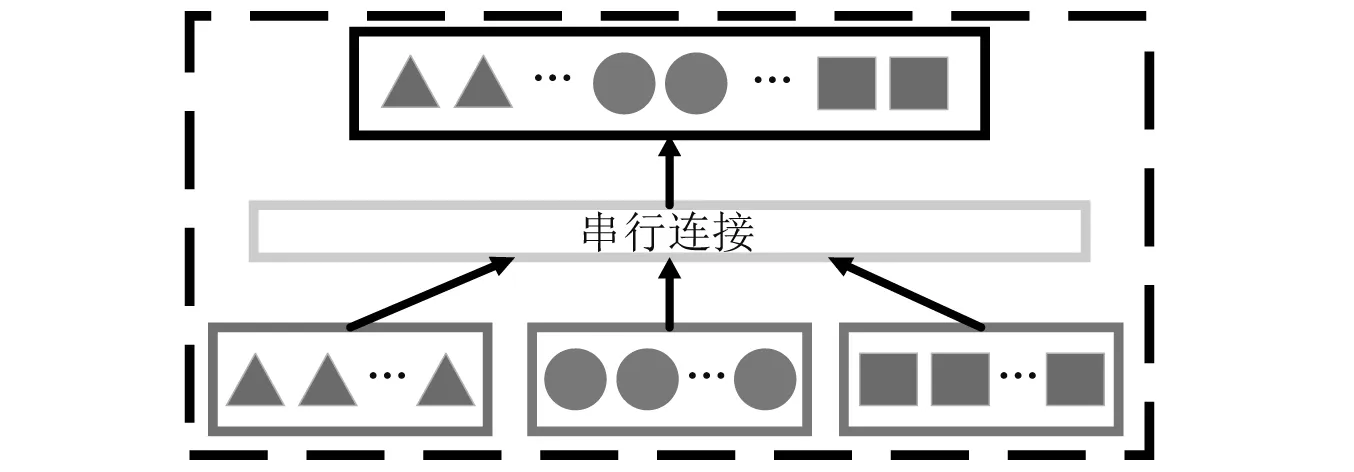
图2 传统结合多网络输出方式

因此本文引入注意力机制[15]，他是模仿人类在观察不同事物时，自动将注意力转移到自己感兴趣部分，而减弱对无关信息的关注，从而提升信息的获取能力，本文提出的融合注意力机制的DBN模型，如图3所示。

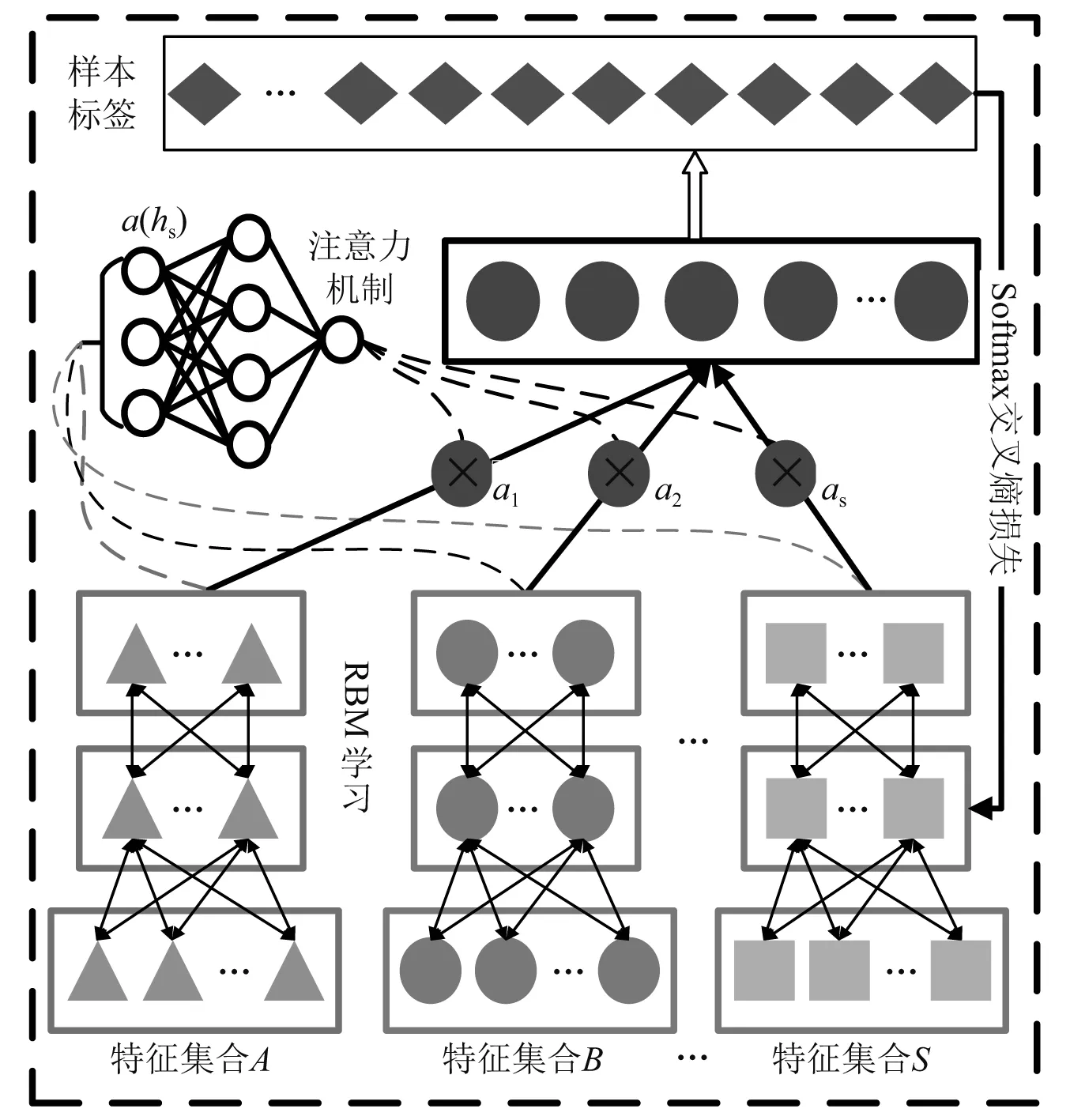
图3 注意力DBN模型

利用注意力机制将1.1节通过RBM后获取的时域、频域、小波包深度特征结合形成齿轮箱故障诊断的全局特征计算为

ui=tanh(Wwhi+bw)

(8)

(9)

(10)

式中：hi分别为时域、频域、小波域深度特征；ai为与之相对应的重要性权值；c为通过注意力机制获得的全局特征。

1.3 模型损失函数改进

余弦损失函数为在Softmax损失函数基础上，保留其扩大类间差异的优势[16]，但减小其对不同信号强度的敏感性，而更加注重向量在方向上的差异，如图4所示。

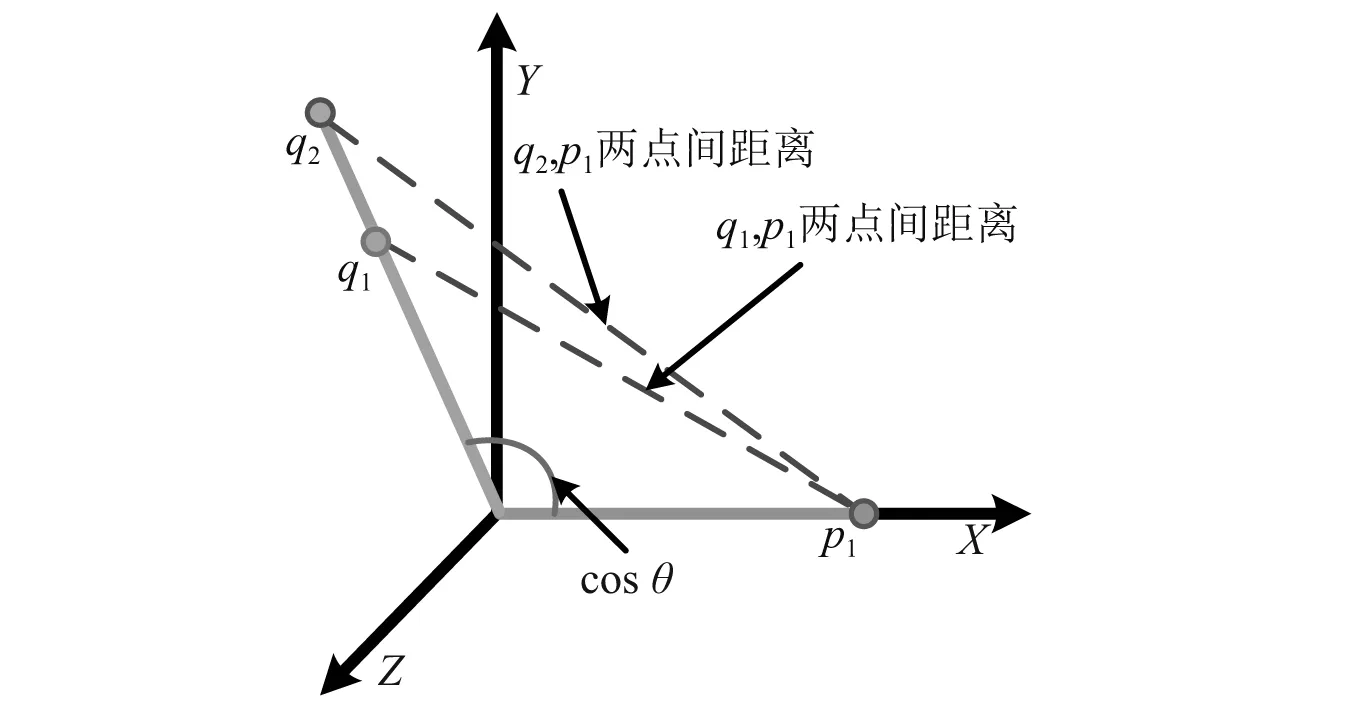
图4 余弦损失示意图

对于相同故障信号q1,q2，其对于故障标签为p1，在以Softmax作为损失函数时，得到最终损失函数Ls如式(11)所示。

(11)

式中：B，N分别为一批次训练样本数与故障类别数；x为隐藏层输出；W为权重矩阵；θ为其间夹角。由式(11)及图3可知， Softmax损失与信号幅值相关。而以1-余弦相似度作为损失函数，得到最终损失函数Lc如式(12)所示。

(12)

由式(12)看出，式中‖x‖2可消去，因此余弦损失与信号幅值无关。因此将余弦损失作为齿轮箱故障诊断损失函数，可将损失从欧几里德空间转换为角空间从而消除信号幅值影响，降低网络的拟合负担。

2 融合注意力机制的改进DBN模型变工况齿轮箱故障诊断流程

设在齿轮箱上采集到的振动信号为s(t)，对s(t)提取时域、频域、小波包特征构成特征集后分别输入至改进后DBN中，利用注意力机制结合各维度深度特征后映射至不同故障类型。完成模型训练后，输入实时采集到的振动信号诊断齿轮箱故障。具体流程如图5所示。

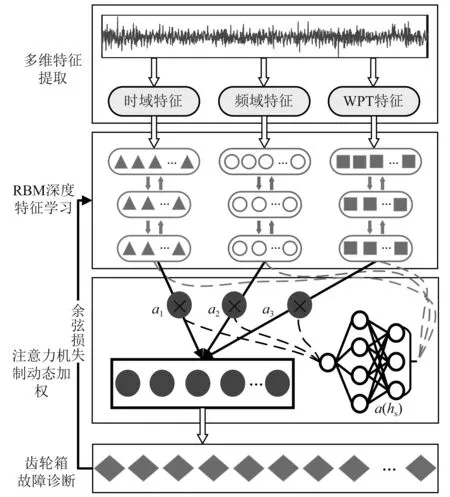
图5 融合注意力机制的改进DBN变工况齿轮箱故障诊断流程

由图5可知，具体步骤为：

步骤1输入采集的齿轮箱振动信号s(t)，提取其峭度、偏度、有效值等11个时域特征，提取其均值频率、一阶重心等13个频域特征；利用小波包变换提取其能量特征，本文采用db5小波进行3层分解；

步骤2利用DBN的贪婪学习方法分别对三个维度特征进行深度挖掘，形成P1,P2,P3三个深度特征集合；

步骤3利用注意力机制对P1,P2,P3进行自适应动态加权形成最终特征集合P，并输入全连接层，完成齿轮箱故障识别；

步骤4利用改进后损失函数对模型进行训练，完成在训练集上齿轮箱故障精确识别；

步骤5对运行中的齿轮箱持续提取振动信号s(t)，按照步骤1～步骤3对其进行处理，从而识别当前齿轮箱运行状态，最后输出齿轮箱故障识别结果。

3 试验验证

为验证所提方法的有效性，本文采用变工况下齿轮箱多类故障诊断试验进行验证。试验台如图6所示，电机通过联轴器驱动齿轮箱轴1，轴间通过斜齿轮(模数= 2.25，压力角= 20°，螺旋角= 20°，Z1=30，Z2=Z3=45，Z4=80)传动，输出轴3通过皮带连接电磁扭矩负载。在箱体上安装加速度传感器采集齿轮箱振动信号，最终通过NI DAQ 6062E采集卡采集数据，采样频率为50 kHz，采样时长为10 s。

图6 变工况齿轮箱故障识别装置

分别在转速为480 r/min，720 r/min，900 r/min、负载为0，10 V，30 V下，分别测试Z3点蚀、Z4齿根裂纹、轴承B1内圈、外圈、滚动体故障等10类故障及一种正常状态，各故障实拍图如图7所示。

图7 齿轮箱各故障图

重复5次试验完成齿轮箱振动数据采集，因此共得到9种工况下11类齿轮箱状态。为便于分析，对每一类故障/正常振动信号各取50组作为测试样本，100组作为训练样本对所提注意力DBN模型进行训练。训练完成后，输入测试数据得到，该方法综合故障诊断率达到99.09%，各分类故障诊断结果如图8所示。

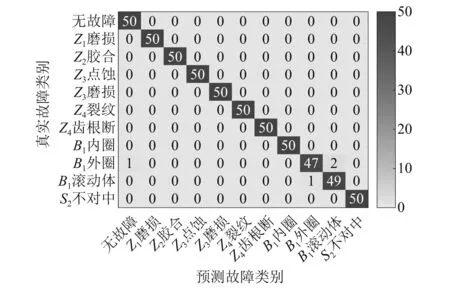
图8 注意力DBN的各类故障诊断结果

为进一步验证所提方法的有效性及泛化能力，将机器学习中经典故障诊断模型SVM、通用深度学习算法BP神经网络及DBN模型应用相同的数据，分别得到其在训练及测试阶段的齿轮箱故障诊断精度与本文提出的方法诊断精度对比，如表1所示。

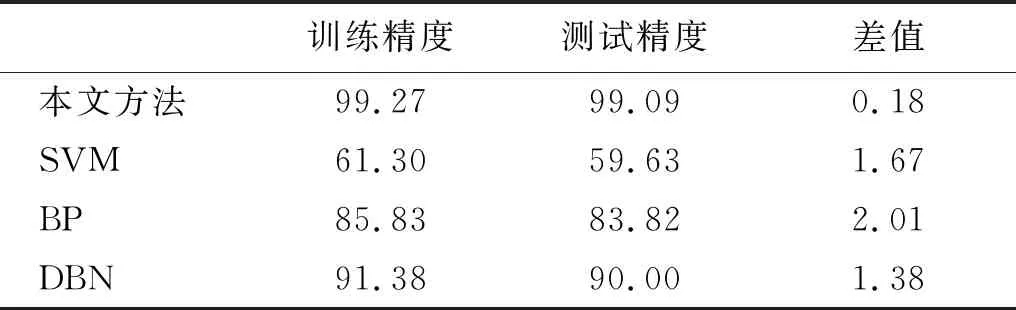
表1 与其他经典故障诊断算法的对比结果

由表1可知，本文中提出的融合注意力机制的改进DBN变工况齿轮箱故障诊断方法具有最高的诊断精度。同时根据训练精度与测试精度的差值列看出，本文方法(0.18%)相比DBN(1.38%)，SVM(1.67%)，BP(2.01%)拥有更强的泛化能力。

分别画出本文提出的方法与DBN方法训练时诊断精度随迭代次数变化曲线，如图9所示。

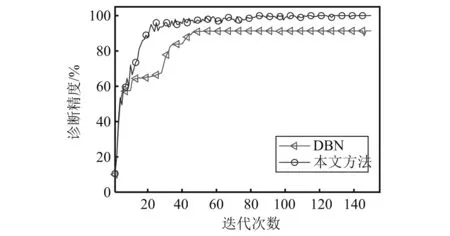
图9 本文提出的方法与DBN方法训练时故障诊断率曲线

由图9可知，本文提出的方法相比DBN更快收敛于较高的诊断精度，因此可减少训练时间。从试验结果可以得知，本文方法在相对提高模型收敛速度与泛化能力的基础上，对变工况齿轮箱故障拥有更高的诊断精度。

为验证所提余弦损失函数关于降低模型对振动信号幅值变化敏感性的效果，同时为与现有研究成果进行对比。本文利用西储大学轴承故障试验数据再次进行验证。试验描述可参见Lu等的研究，本文以2 048个点长度截取故障信号，采用负载工况为2 238 W时样本作为训练集，负载工况分别为0，746 W，1 492 W时样本作为测试集，测试在变负载工况下包含不同缺陷大小的各故障模型识别精度。得到各类故障识别精度如图10所示，其中1～4分别代表正常运行、内圈故障、外圈故障、滚动体故障四种运行模式。

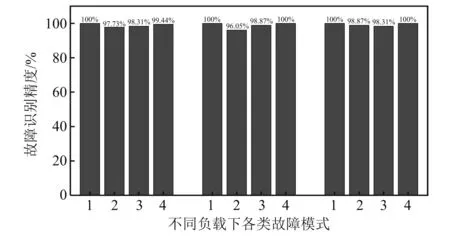
图10 不同负载下轴承各类故障识别精度

由图10可知，本文所提方法对于训练时未出现过的负载工况也有着很高的故障识别精度。为可视化故障特征学习过程，引入t-SNE对所提模型的轴承故障特征输入层、注意力动态加权输出层、全连接层特征进行三维可视化，结果如图11所示。

由图11可知，随着故障特征经过注意力动态加权输出层、全连接层，不同类别故障间分布边界逐渐清晰，可分性逐渐增加。在全连接层几乎全部可分，实现故障的准确识别。

图11 各层特征的t-SNE可视化

与已发表的现有研究成果进行对比，对不同工况下(0～1 492 W)相同故障模式识别结果求和取平均后作为该类故障模式的总体识别精度。表2给出了各类故障识别方法对不同故障模式详细的识别结果。

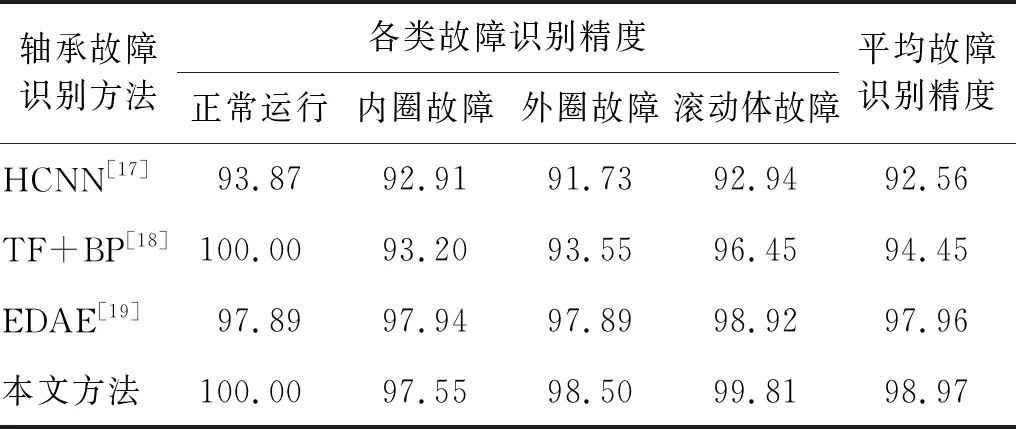
表2 现有方法与本文所提方法的故障识别精度对比

由表2可知，本文所提方法相比深度自编码器方法、卷积神经网络方法等具有更高的故障识别精度，证实了所提方法的有效性。

4 结 论

针对在变工况运行条件下，齿轮箱故障难以识别且精度降低的问题，本文提出融合注意力机制的改进DBN变工况齿轮箱故障诊断方法。通过试验验证及与其他常用故障诊断方法对比，结果表明：

(1) 该方法在利用时域、频域、小波包等多维度特征的基础上，利用注意力机制融合深度特征，有效提高了变工况环境下齿轮箱故障诊断的精确度。

(2) 通过改进DBN模型损失函数，降低了模型对故障信号幅值的敏感性，因此减轻了网络拟合负担、提高了泛化能力。

在未来工作中，将对于实际生产中数据缺乏标签问题，利用DBN模型的无监督学习能力，搭建半监督故障诊断模型，减少对标签数据的依赖。