摩擦对滚动碰撞式调谐质量阻尼器的影响及其试验研究

李书进， 伍大涛， 阳昌娟， 孔 凡， 张远进

(1.武汉理工大学 土木工程与建筑学院，武汉 430070; 2.武汉理工大学 安全科学与应急管理学院，武汉 430070)

结合碰撞阻尼思想，本课题组在滚动型调谐质量阻尼器(tuned rotary mass damper, TRMD)[1]的基础了提出了一种滚动碰撞式调谐质量阻尼器(pounding tuned rotary mass damper, PTRMD)装置，并对其减振性能进行了探讨[2-3]。该装置由球形振子、弧形轨道及黏弹性限位装置组成，当振子滚动幅度不大，与限位装置无接触时，功能与TRMD无异；当振子滚动幅度大到与限位装置发生撞击时，碰撞阻尼发挥作用，实现能量耗散。实际上，PTRMD兼有调谐阻尼器和碰撞耗能(如颗粒阻尼器[4])的特点，可视为非线性动力减振器的一种，已有研究表明，非线性动力减振器能够在较宽的频带范围内有效吸收主体结构的振动能量[5-6]，是提高传统TMD控制性能的有效途径之一。

影响PTRMD减振性能的参数较多，如振子质量、轨道半径、碰撞材料、限位装置间距、振子与轨道间的滚动摩擦因数等，对这些参数开展研究对于该装置减振理论的完善和应用推广都具有十分重要的意义。李书进等对其中的多数参数进行了探讨，分析了它们的影响特性和规律，但对于滚动摩擦的影响，由于其机理复杂，且摩擦力一般为非线性项，受控系统求解困难而未做深入分析，在前期的研究工作中均作了轨道面为光滑的假定。事实上，PTRMD中的滚动摩擦有一定程度的能量耗散，对减振性能的影响很大，实际中也并不存在完全光滑的轨道，国内外的研究也表明摩擦耗能也能起到消能减振的作用，并提出了相关计算模型和带摩擦的减振装置[7-9]，因此，对该问题进行深入研究既重要也必要。

对PTRMD中的滚动摩擦效应问题进行了理论和试验研究。首先，引入摩擦耗能机制，建立考虑滚动摩擦耗能的PTRMD控制方程，通过对方程进行数值求解分析了振子与轨道间的滚动摩擦对阻尼器减振性能的影响和大概规律；然后，选用不同质地的材料粘贴于滑道表面，通过试验对振子与滑道间的滚动摩擦因数进行测定，并进行振动台试验，对其在自由振动、强迫振动及地震激励等工况下的摩擦效应进行探讨。

1 考虑滚动摩擦影响的PTRMD动力方程

1.1 计算模型

装有PTRMD的单自由度结构简化模型，如图1所示，在外力作用下，结构在产生水平方向位移的同时带动PTRMD中的振子产生滚动，受控结构能量以动能和势能的形式转移到小球中，并通过冲击阻尼和滚动摩擦耗散。通过对PTRMD的轨道半径、振子材料和半径等参数的合理设计，可使PTRMD对结构振动进行有效的控制。PTRMD模型见图2。

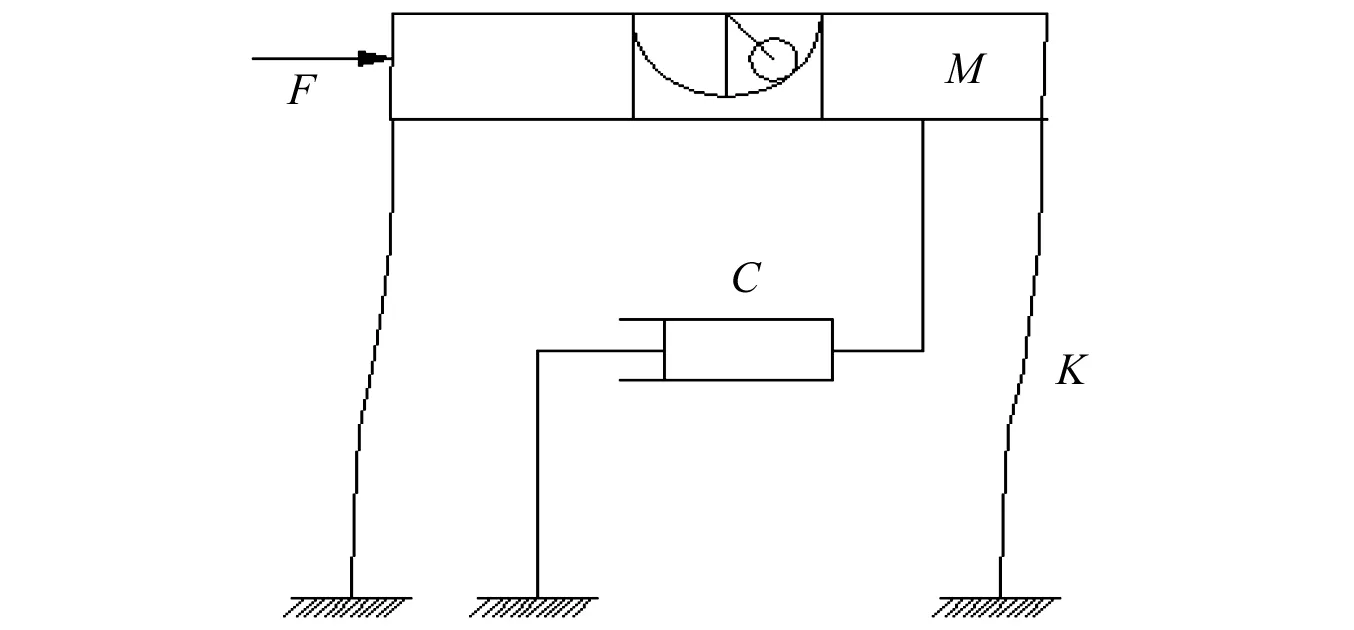
图1 带PTRMD结构模型

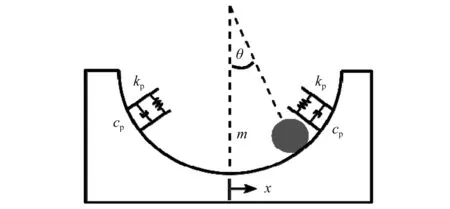
图2 PTRMD振子的运动模型

1.2 运动方程的建立

采用Lagrange变分原理推导该受控体系的动力方程

(1)

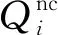
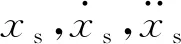
1.2.1 无碰撞阶段

当θ≤|θm|时，振子与限位装置不发生接触，PTRMD的表现与TRMD相同，此时受控体系动能包括主体结构的动能、PTRMD振子平动及绕自身球心转动的动能，即

(2)

受控体系势能V包括受控结构弹性势能和PTRMD振子重力势能，即

(3)

非保守力所做虚功包括外力做功、结构阻尼力做功以及滚动摩擦力矩做功

(4)

式中：δx，δθ分别为x，θ位移方向的虚位移；Mf为振子与轨道间滚动摩擦产生的滚动摩擦力矩，与振子运动方向相反，其表达式为

(5)

(6)

考虑振子转角位移θ为小量，将式(2)、式(3)及式(6)代入Lagrange运动方程，得到该阶段受控体系的控制方程

(7)

(8)

整理为矩阵形式

(9)

1.2.2 碰撞阶段

当θ≥|θm|时，振子将与轨道上的黏弹性限位装置发生碰撞。此时，受控体系动能的计算公式不变，仍为式(2)，而势能及非保守力做功发生改变。由于球形振子与黏弹性材料在碰撞过程中会发生一定的变形，受控体系势能应考虑由于黏弹性材料变形产生的弹性势能，而非保守力做功应考虑碰撞接触面上的阻尼力所做的虚功。采用非线性黏弹性碰撞模型模拟PTRMD中的非线性碰撞，该模型认为碰撞时能量损失只发生在材料压缩阶段，恢复阶段不存在能量耗散[10]。则受控体系的势能及非保守力所做虚功为

(10)

(11)

(12)

代入式(1)得到碰撞阶段的控制方程为

(13)

(14)

整理为矩阵形式，有

(15)

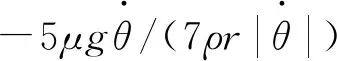
1.3 滚动摩擦影响分析

利用四阶Runge-Kutta法对式(9)和式(15)进行数值求解，以单自由度受控结构的自由振动为例对PTRMD中滚动摩擦的影响进行分析，式中各参数的取值见表1。由于控制方程式(9)和式(15)是以PTRMD中振子与限位装置发生碰撞时的角度θm来区分的，该参数的取值对阻尼器的影响很大，计算中将改变其值，以探讨与滚动摩擦因数间的相互影响。

表1 受控结构参数

将θm在0～0.5 rad、滚动摩擦因数在0～0.01 m变动，方程初始条件取初位移x0=0.02 m，PTRMD振子初位移θ0=0，即振子最初静止在弧形轨道底部。引入受控结构位移时程的均方根Prms作为PTRMD的减振控制指标，计算得到的结构Prms与碰撞角度及滚动摩擦因数关系，如图3所示。从图可知，滚动摩擦因数对各碰撞角度下受控结构Prms的影响呈现相同规律：在小摩擦因数范围内，Prms随摩擦因数的增大而减小，滚动摩擦耗能显著；但当摩擦因数大到一定程度后，均方根Prms反而增大，PTRMD的减振效果变差，表明PTRMD存在最优的滚动摩擦因数区间，对本例约在0.003 5附近。

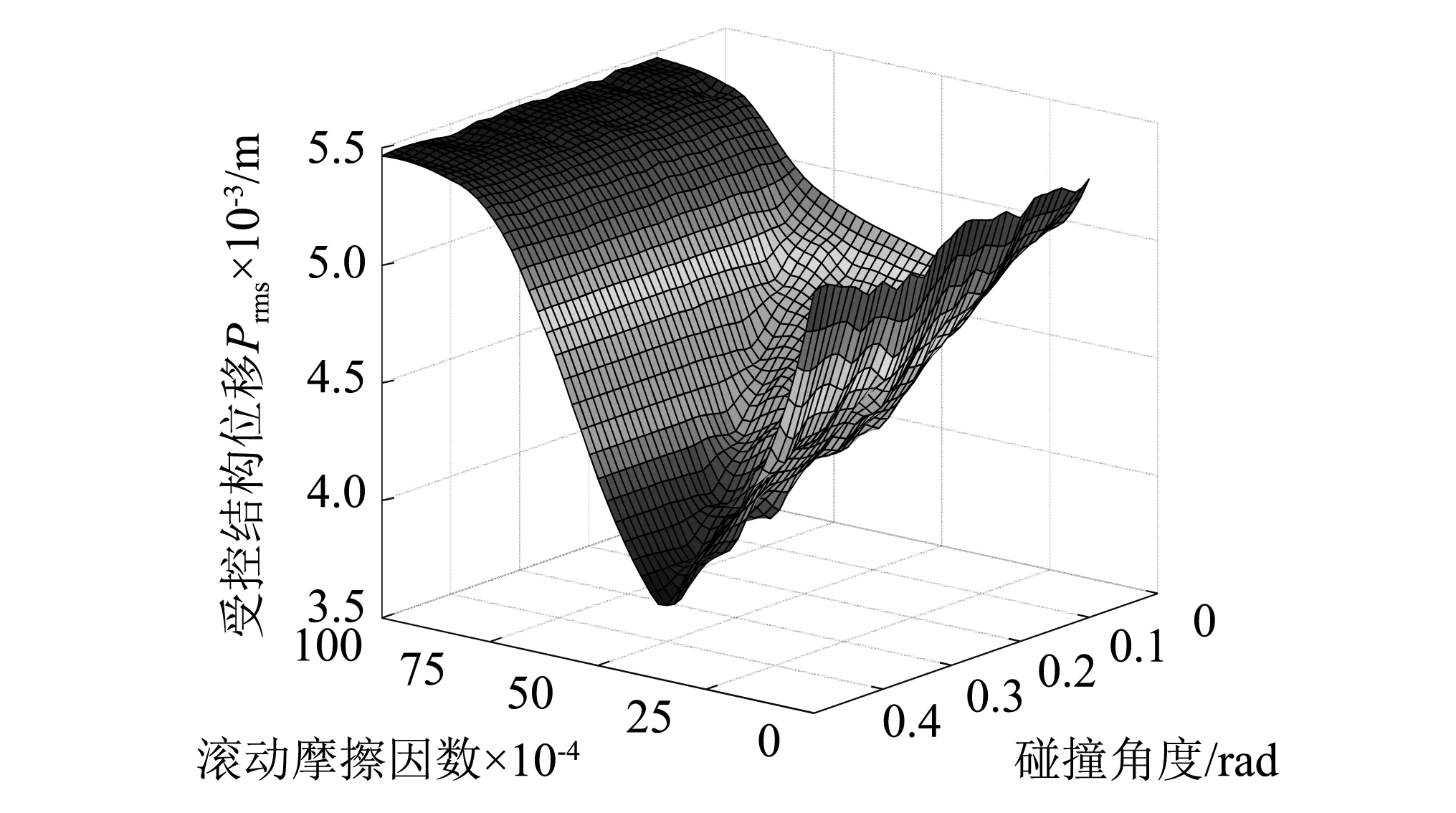
图3 受控结构Prms与θm及滚动摩擦因数关系图

围绕最优摩擦因数区间选择一组摩擦因数：0，0.002，0.003 5，0.006，0.008，取碰撞角度θm为0.4 rad，计算得到各摩擦因数下的位移衰减情况，如图4所示。可以看出，摩擦因数为0.003 5时PTRMD的控制效果最好，摩擦因数过大或过小均会使其减振效果变差。

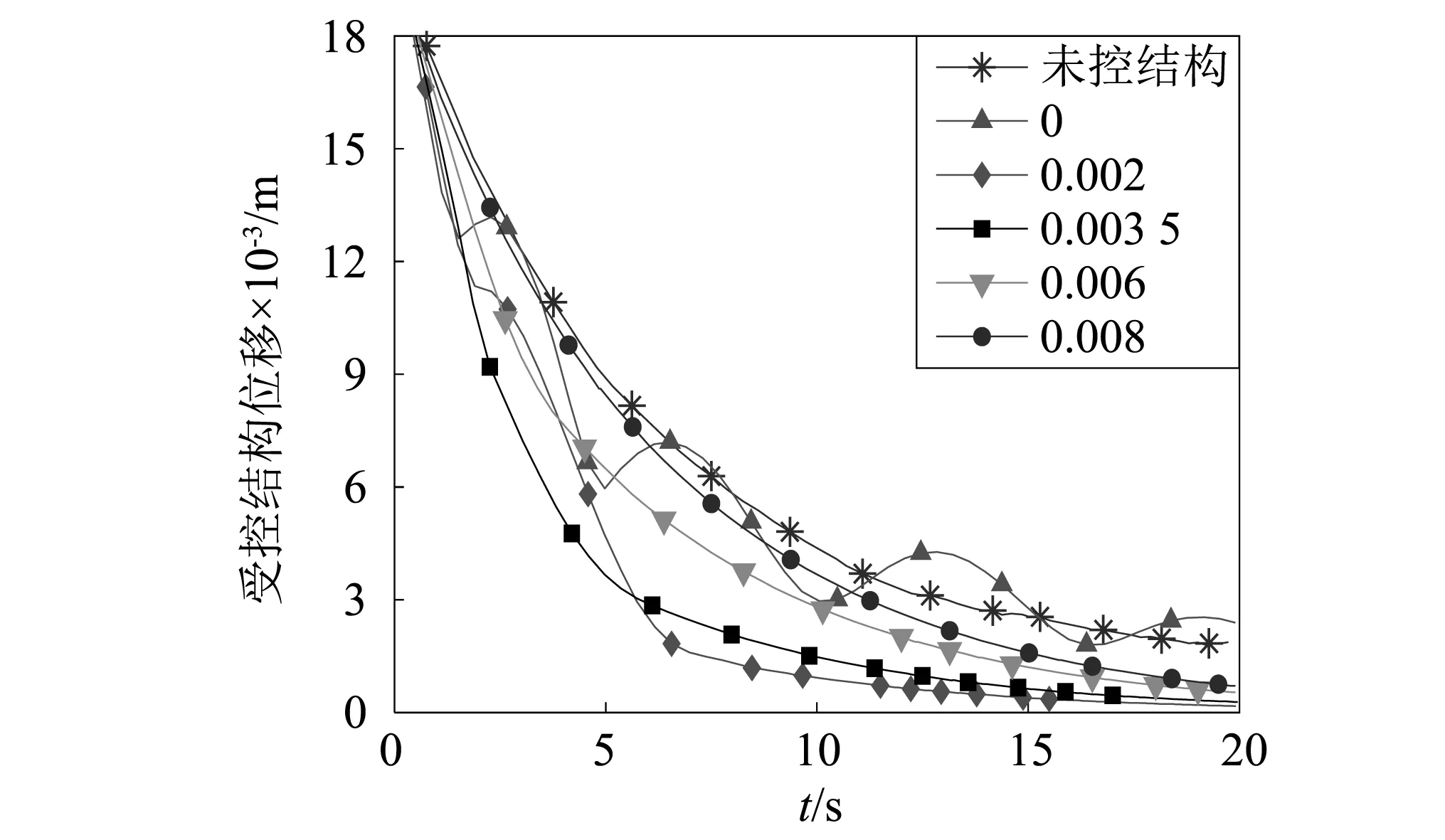
图4 不同摩擦因数下结构位移衰减图

通过对振子的运动轨迹进行分析，发现摩擦因数为0，0.003 5及0.008时振子与壁发生碰撞的次数分别为8次、3次和0次，碰撞次数随滚动摩擦因数的增大而减少。光滑情况下振子滚动激烈，由于能量仅靠碰撞耗散，非常缓慢，导致后期即使结构振动幅度变小，在振子带动下仍有周期性晃动(见图4)，因此适当加大振子的摩擦耗能能有效改善PTRMD的减振性能；但如果滚动摩擦过大，振子的滚动受到限制，PTRMD又无法充分发挥其作用，因此，选择合适的摩擦因数，使碰撞冲击和滚动摩擦耗能均能得到充分发挥，对于PTRMD尤为重要。

2 试验研究

2.1 结构模型

对一装有PTRMD的单自由度结构进行摩擦影响试验研究，主结构为单层门式钢框架模型，由两块不锈钢板作立柱，顶上固结厚度较大的横梁以确保其满足刚度无穷大假定，具体参数见表2。PTRMD居中设置在梁上，质量为700 g，与横梁一起作为结构质量快。制作好的模型见图5，经实测，结构模型自振频率为1.35 Hz。

图5 结构模型

表2 试验模型参数

2.2 PTRMD设计

PTRMD主要由球形振子、弧形轨道及黏弹性限位壁构成。试验中弧形轨道用铝合金制作，球形振子为铸铁材料。限位壁用铝合金制，表面涂5 mm厚的硅橡胶，固结于轨道上。

类似传统TMD，将PTRMD自振频率调谐至受控结构基频附近，且球形振子与受控结构的质量比取0.02～0.05时减振效果最佳[11-12]。而振子的滚动频率只与轨道半径和小球半径的差ρ有关，其计算公式为[13]

(16)

将主结构自振频率代入即可得到PTRMD的各参数见表3，阻尼器实体模型见图6。

表3 PTRMD参数设置

图6 试验用PTRMD

2.3 滑道面材料及其滚动摩擦因数测量

选用不同质地的面料粘贴于上述制作好的PTRMD滑道表面，通过试验对振子与滑道间的滚动摩擦因数进行测定。为探讨PTRMD的最优摩擦因数范围，选取砂纸(600Cw)、海绵(低中高三种密度)、EVA泡棉胶、硅橡胶及橡胶共7种摩擦材料，趋势由质地较硬、不可变形向质地较软且易变形，耗能能力和阻尼性能愈好的黏弹性材料变化，具体见表4。

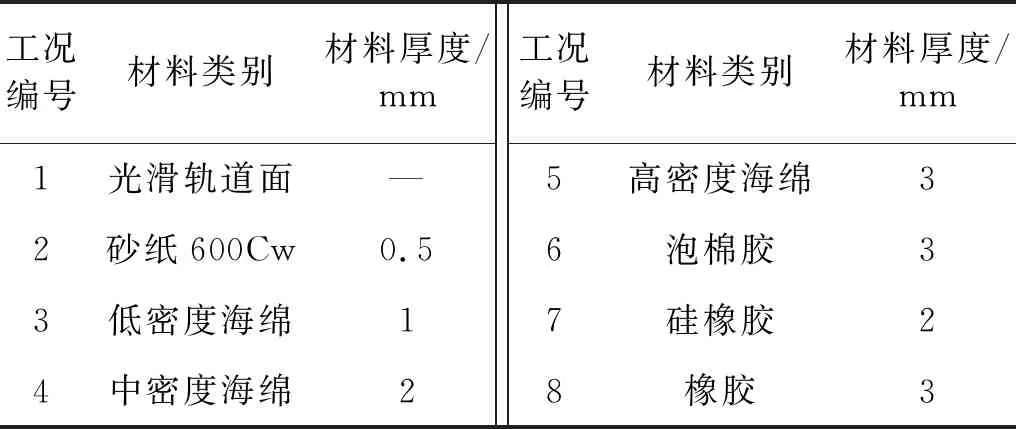
表4 滚动摩擦特性试验工况

由于球形振子是在弧形轨道上滚动，动力参数难以测量，本文采用高速摄像技术记录振子运动，再进行数据提取[14]。测量模型与装置如图7，原理及过程说明如下。

图7 PTRMD滚动摩擦测试试验

在轨道面粘贴不同摩擦材料，将质量为m的振子在半径为R的弧形轨道顶端静止释放，小球在轨道面内做往返运动直至静止。基于能量守恒定理，小球在弧形轨道运动过程中的动能变化ΔEk、重力势能变化ΔEv及摩擦力做功Wf三者关系式为

ΔEk+ΔEv=Wf

(17)

令小球在轨道上速度为零的点为极值点，对应的转动弧度为θi。任取两个极值点θl，θn，则小球在该弧段范围内的能量变化为

(18)

ΔEv=mgρ(cosθl-cosθn)

(19)

(20)

采用高速摄像仪器记录小球在弧形轨道的运动轨迹，然后进行图像边缘检测，捕捉小球质心位置，得到小球在弧形轨道内运动的时程曲线，结合式(17)可求得小球与轨道面间的滚动摩擦因数。每种材料做三组试验，取其平均值。

2.4 振动台试验

利用小型振动台对受控模型结构进行减振试验，探讨PTRMD在不同摩擦材料下的减振效果和影响规律。加载方式有自由振动、强迫振动和地震激励三种，其中，地震激励选用了El Centro波、Kobe波和Northridge波三条地震波，各地震波的特性见表5。

表5 地震波特性

将模型底部通过螺栓固定于振动台面，在结构顶部及振动台面分别布置一个加速度传感器用于采集模型顶部和底部的水平向加速度，同时在同一高度分别布置一个激光位移传感器来测量结构顶部和振动台面的水平位移，试验模型与仪器布置如图8所示。

图8 试验模型及仪器布置

3 试验结果分析

3.1 滚动摩擦特性

限于篇幅，这里仅以硅橡胶轨道面为例阐述数据处理过程。取其中某时刻图像，对其进行灰度化处理，然后高斯滤波去噪。采用Canny算子[15]对滤波后的图像进行边缘检测和轮廓提取，该算法是一阶微分算子的优化算法，需要参数较少且计算效率高，能得到连续完整的振子边缘[16]，获取连通区域特征并标记球心及轨道圆心。处理的具体流程见图9，得到的振子在弧形轨道内的动力响应见图10，由此即可得到硅橡胶面时振子的滚动摩擦因数。

图9 图像处理流程

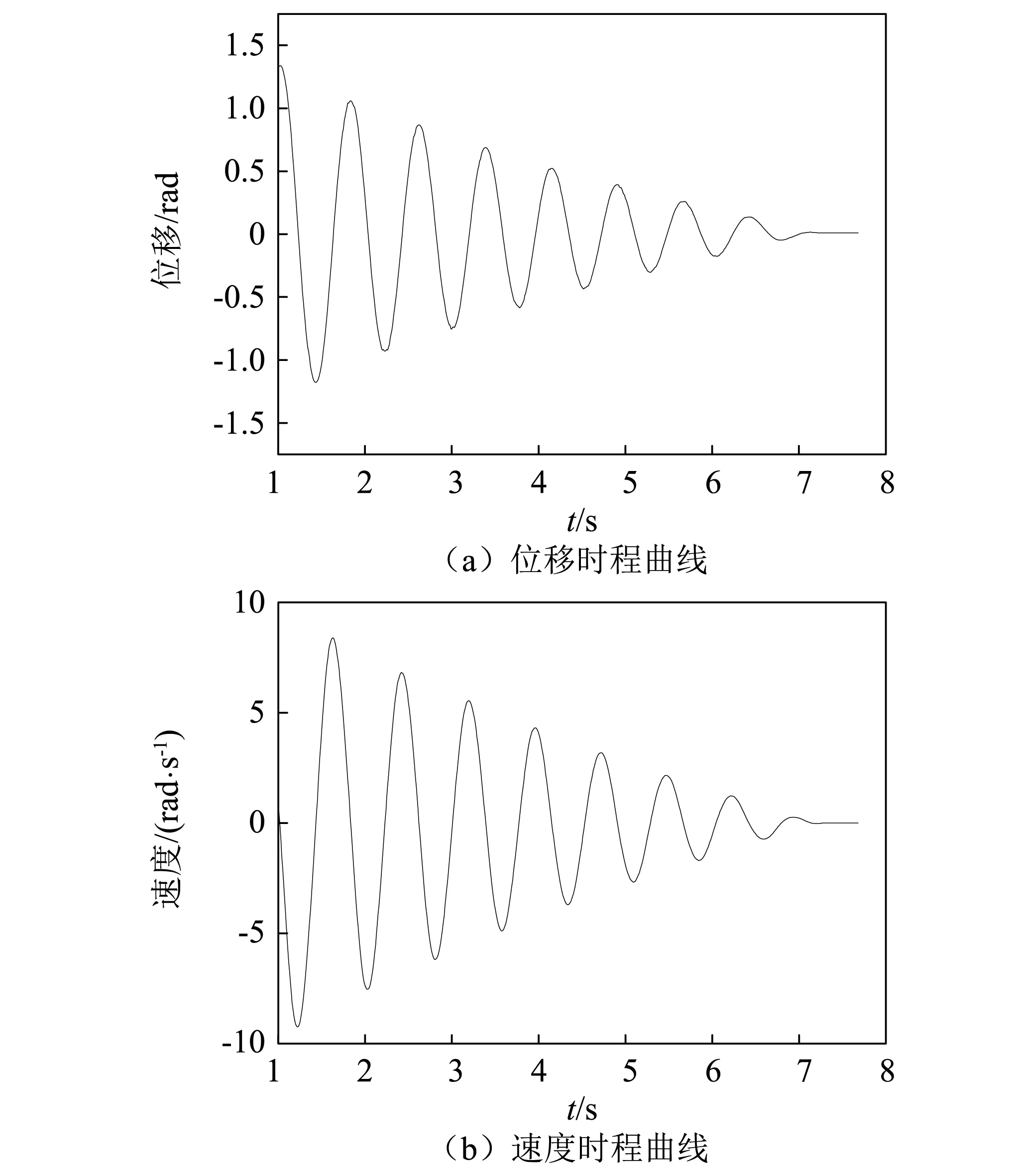
图10 振子动力响应图

试验中观察到，同一高度自由滚落，球体在光滑轨道、砂纸这两种较硬材料上的滚动幅度大、时间较长，噪声较也大；在泡棉胶、硅橡胶、橡胶和高密度海绵等质地较软、具有较好回弹性的材料上运动稍缓和，材料发生细微凹陷回弹；在低、中密度海绵上运动受到明显阻力，仅滚动两个来回便静止于轨道最低处，材料发生明显变形。时间上，球体在光滑轨道上滚动16 s才能静止，位移衰减最慢，而在中密度海绵轨道面上仅2 s就停止，衰减最快。实测各材料的滚动摩擦系数见下表。

3.2 自由振动

对无控结构和不同轨道面摩擦材料的受控结构进行自由振动试验，初始位移均为7 cm，测得各材料下框架顶部位移衰减包络如图11所示。可以看出，无控制时，结构位移衰减缓慢，直到20多秒后才衰减至50%，而装有阻尼器的受控结构在振动初期位移的衰减幅度就较大，均在10 s内衰减至50%。从图还可以看出，合理增大摩擦因数能有效提高PTRMD的减振性能，其中，中密度海绵轨道面PTRMD的减振控制效果最佳，在第4 s时已将结构振幅衰减至58%，不过后期的控制效果不如低密度海绵轨道面(见图12)。根据以上分析和试验过程中的观察可知，轨道面摩擦因数越大，结构振幅衰减速度就越快，但当摩擦因数过大时，振子在结构振动后期滚动幅度较小甚至无法滚动，此时PTRMD无法发挥其调谐减振作用，减振效果变差。图13为不同摩擦因数下框架顶部位移频谱图，可以看到，摩擦因数越大的材料频谱幅值越小，表明受控的频带要宽，即合理增大轨道面摩擦因数能有效增加PTRMD的控制频带宽度。

表6 振子与不同摩擦材料间的滚动摩擦因数

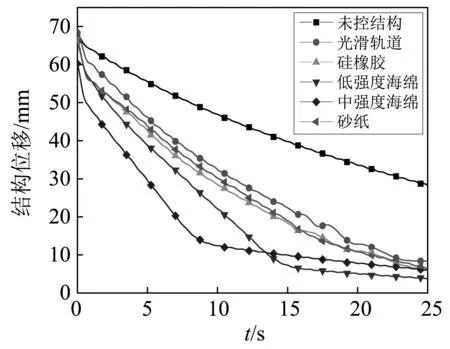
图11 自由振动位移衰减包络图

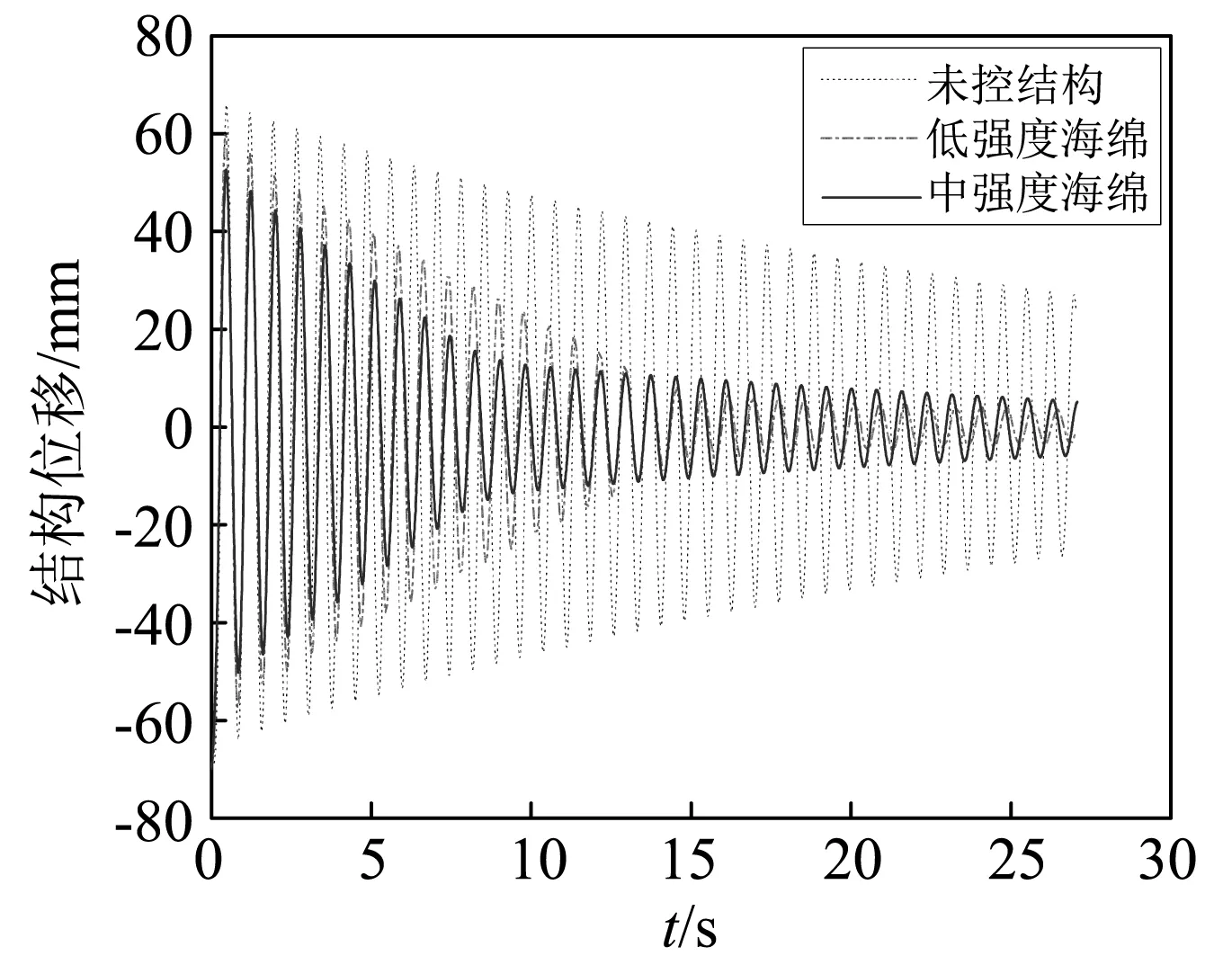
图12 中、低密度海绵时自由振动响应对比

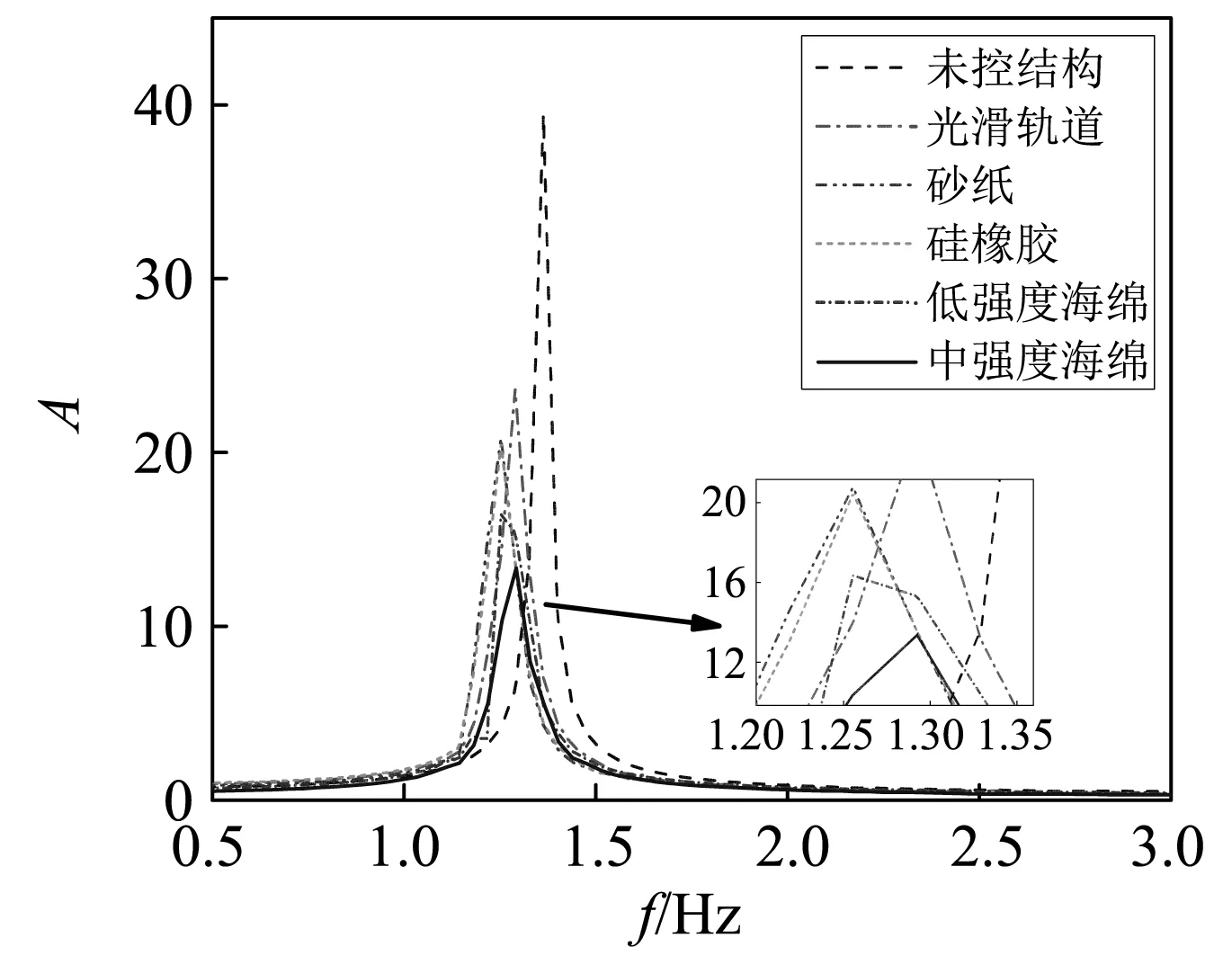
图13 自由振动位移频谱图

3.3 强迫振动

利用振动台给模型施加简谐激励，将激励频率调为与结构基频相同，即f=1.35 Hz，探讨不同滚动摩擦下PTRMD对结构共振的抑制情况，简谐激励的幅值均为0.5 cm。

试验中可观察到，在惯性力作用下，PTRMD球形振子由静止到开始滚动并发生碰撞存在一定的时间差，因此在激励作用的前几秒，PTRMD的减振效果并不明显。随着激励的不断输入，结构振动幅值不断增大，振子的滚动幅度变大，并开始不断与限位壁发生碰撞，逐渐发挥PTRMD的良好减振性能，结构位移响应衰减明显，有效地抑制了结构的共振响应。但当滚动摩擦因数过大时，同等激励下振子的滚动路径变短且碰撞次数明显减少，减振性能有所下降。图14为采用低密度海绵和中密度海绵时结构反应的对比图，可以看到，在整个简谐激励作用时程内，滚动摩擦系数稍低的低密度海绵轨道PTRMD对结构位移的控制效果要优于滚动摩擦因数稍高的中密度海绵PTRMD。此外，相较其他几种滚动摩擦因数更小的材料，低密度海绵轨道面的减振效果又要明显优于它们。由此表明，与自由振动相似，PTRMD存在最佳的滚动摩擦因数区间，不过该区间表现比较复杂，与结构形式、激励类型和大小以及阻尼器本身参数有关。

图14 中、低密度海绵时简谐激励响应对比

3.4 地震波激励

选用El Centro波、Kobe波和Northridge波等实际强震记录对模型结构进行加载，试验时将所选地震波的加速度峰值均设定为310 cm/s2。试验结果可知，不论何种地震激励，在一定范围内滑道的滚动摩擦因数越大PTRMD的控制效果就越好，表明合理地增大轨道面的滚动摩擦能在一定程度上改善PTRMD的工作性能。但试验也同样发现滚动摩擦因数也不能太大，过大的摩擦因数会显著降低其控制能力。图15～图17分别为三种地震波下采用低密度海绵和中密度海绵轨道时结构反应的对比图，可以看出，滚动摩擦因数稍大的中密度海绵轨道在地震作用初期对位移及加速度的抑制效果要优于低密度海绵，但地震作用后期的效果却不佳。究其原因可知，地震作用前期结构输入的能量较大，带动PTRMD剧烈振动，轨道面摩擦阻力实现了良好耗能；而在地震作用后期，结构输入能量减小且振幅衰减，此时轨道面的摩擦阻力反而限制了振子的滚动，控制效果变差。

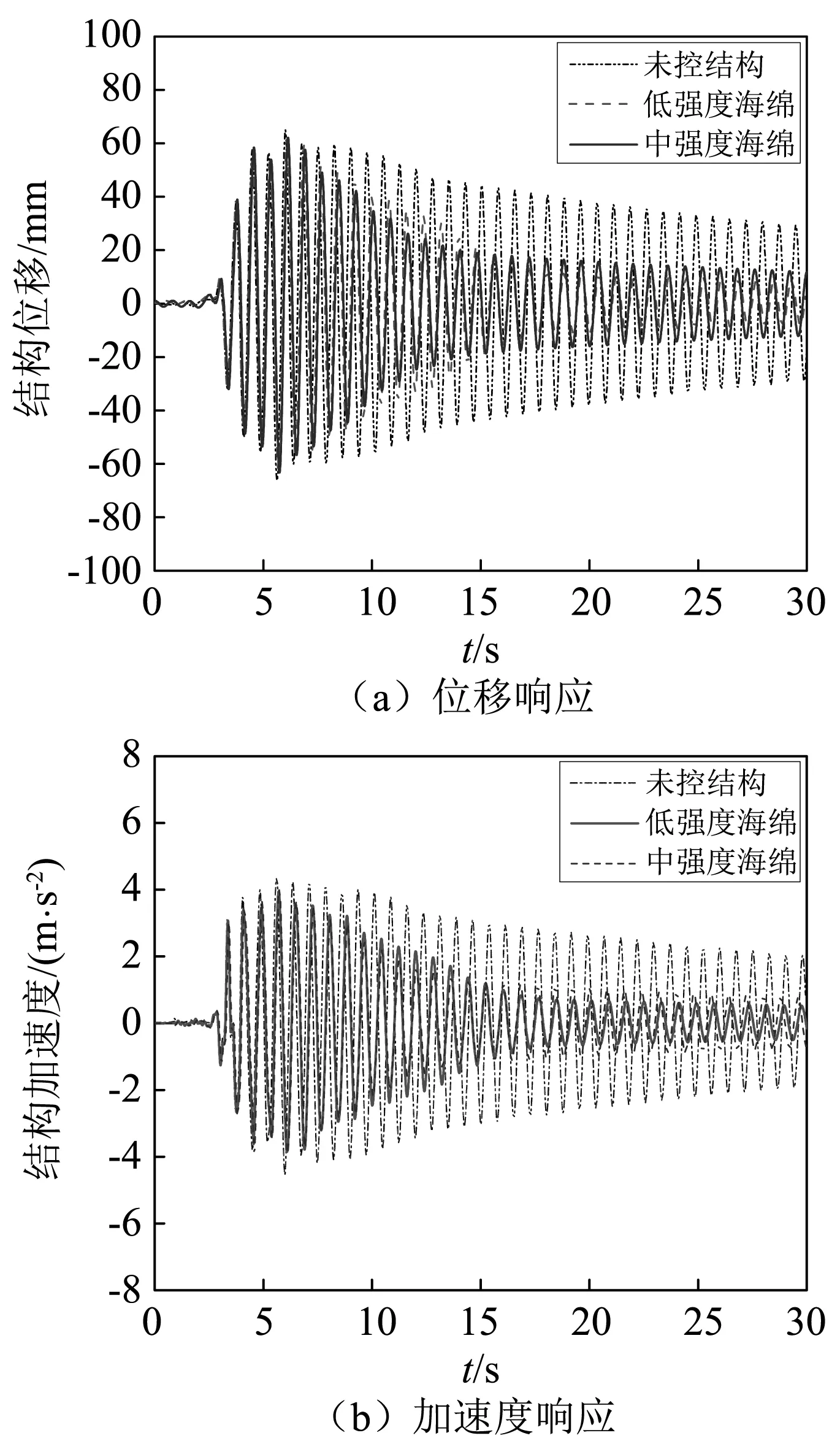
图15 El Centro波作用下中、低密度海绵轨道响应对比

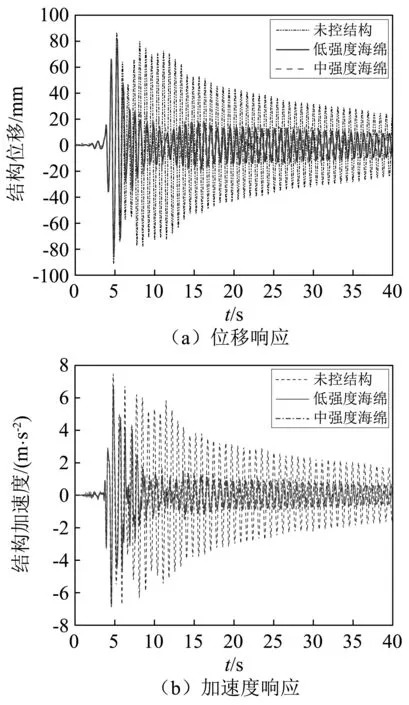
图16 Kobe波作用下中、低密度海绵轨道响应对比

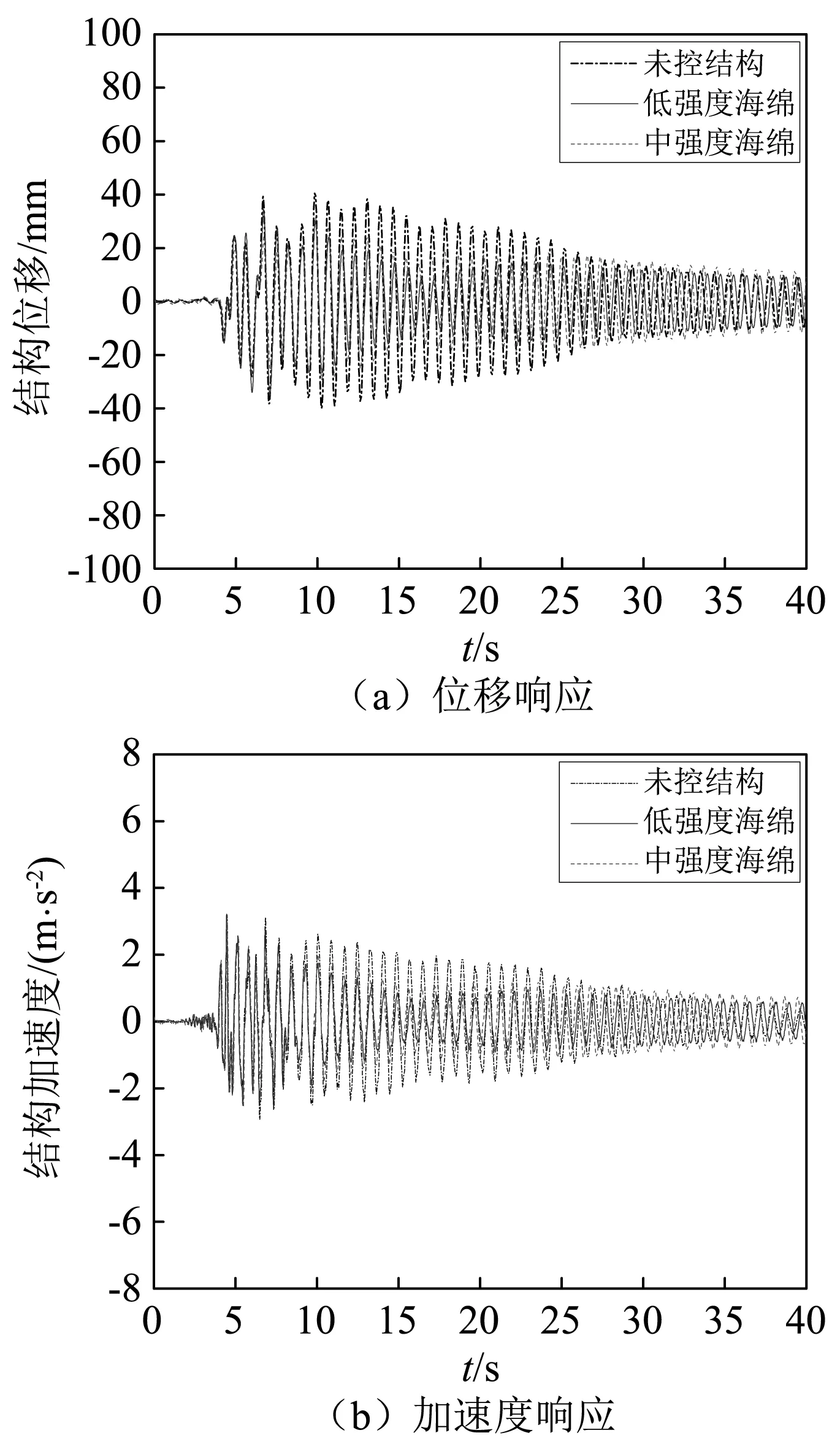
图17 Northridge波作用下中、低密度海绵轨道响应对比

此外，图中还可看出，不同的地震波激励下PTRMD的减震效果有所不同，其中对Kobe波的减震效果最好，El Centro波次之，Northridge波较差。结合三种地震波的频谱特性可知，Kobe波的能量主要集中在1.0～1.5 Hz[17]，较为集中且与本试验模型框架自振频率(1.35 Hz)十分接近，框架反应较大，阻尼器控制作用明显，减震效果显著；El-Centro波的能量分布稍均匀，主要分布在1.0～2.5 Hz内，高于结构的基频，但阻尼器的控制效果也较好，表明PTRMD对于频率高于结构自振频率的激励也具有较好的控制能力；而Northridge波的能量主要集中在0.5～1.0 Hz[18]，比结构自振频率小，结构的反应不大，PTRMD的减震效果也不佳，特别是振动后期基本没什么减震甚至还有放大现象。以往的研究也表明，碰撞类阻尼器在激励频率比结构自振频率小时往往鲁棒性不佳，振子与结构发生同向碰撞现象增多，会导致结构响应加大[19-20]。

4 结 论

对滚动碰撞式调谐质量阻尼器中振子与轨道间的滚动摩擦对阻尼器的性能影响进行了理论和试验研究。引入摩擦耗能机制，利用Lagrange变分原理建立了考虑滚动摩擦耗能的PTRMD控制方程，通过对方程进行数值求解分析了滚动摩擦对阻尼器性能的影响；通过试验测定了不同质地滑道面材料的滚动摩擦因数，并进行了振动台试验，分析在自由振动、强迫振动及地震波激励等工况下PTRMD中的摩擦效应，得到的主要结论如下：

(1)对PTRMD的数值分析表明振子与轨道间的摩擦耗能能有效改善其减振性能，且PTRMD存有最优的滚动摩擦因数区间，太小或过大均不利于结构的减振。

(2)采用高速摄像和计算机图像处理技术能对非直线滚动振子的运动轨迹进行精准的采集。

(3)摩擦效应能提高PTRMD的耗能能力，有效改善其工作性能，但滚动摩擦因数存在最优区间，且该区间表现比较复杂，与结构形式、激励类型和强弱以及阻尼器本身参数有关。