变拓扑空间可展桁架多体系统动力学建模与分析
2021-07-22黄泽兵刘锦阳袁婷婷
黄泽兵, 刘锦阳, 袁婷婷, 侯 鹏
(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240;2.上海卫星装备研究所,上海 200240)
高分辨遥感观测在气候监测、地形测绘、陆地资源研究、环境与灾害监测以及军事侦查等诸多领域都起着非常重要的作用[1],太空望远镜是实现实时高分辨率遥感观测的重要途径,由于受到航天运载工具空间和载重的限制,太空望远镜在发射前处于折叠状态,当发射到太空在特定轨道位置释放,随后在自身动力源的驱动作用下完全展开至伞形。其展开的关键一步是三根桁架并行展开把主镜推送至特定位置,然而,由于桁架构件繁多,展开长度达数十米,该展开过程呈现出复杂的动力学特性,尤其是在桁架单元展开锁定的瞬间对星体与主镜产生巨大冲击,甚至使系统结构造成破坏,因此有必要开展太空望远镜桁架展开动力学的研究。
截至目前,已有不少学者对空间可展机构进行了展开动力学相关的研究。例如:Guo等[2]采用Jourdain速度变化原理建立了地面太阳能帆板系统的动力学方程,研究了大型柔性太阳能帆板系统的地面展开动力学特性,通过与ADAMS仿真结果对比验证了动态模型的有效性;Chunmei等[3]建立了含间隙柔性四连杆机构的动力学模型,研究了关节处间隙与摩擦对机构展开动力学的影响;Wallrapp等[4]建立了可展太阳帆板的柔性多体动力学模型,通过采用SIMPACK程序对柔性太阳帆板展开动力学特性进行了分析,研究了太阳帆板的柔性效应地驱动机构的影响;邱雪松等[5]建立了月球车两级往复可展太阳帆板的柔性多体动力学模型,并分析了间隙和柔性对帆板展开动力学的影响;杨淑利等[6-7]基于Kane法多体动力学基本理论及Hertz接触理论建立了考虑根铰间隙的框架展开机构多体系统动力学模型,分析了框架展开机构铰链间隙与驱动力相互作用的动力学规律;游斌弟等[8]利用Lagrange和Newton方法建立了卫星太阳阵系统的多刚体动力学模型,研究了铰链副接触碰撞对太阳阵展开及卫星姿态的影响;赵孟良等[9]采用两个节点笛卡尔坐标描述刚体的方法建立了周边桁架式可展天线的多刚体动力学模型,并考虑摩擦对周边桁架式可展天线进行了展开动力学分析。以上展开动力学的研究对象大多为结构相对简单且物体数量较少的机构。此外,多体系统动力学的建模方法一般采用笛卡尔方法[10-13],取浮动坐标系的基点位置坐标、姿态角坐标和模态坐标为广义坐标,并引入相邻柔性体之间的约束方程,建立多体系统的微分-代数混合方程。由于这种方法的广义坐标数和约束方程个数较多,不适合于计算规模较大的柔性多体系统的数值仿真。而随着高分辨遥感观测技术的高速发展,太空望远镜一方面结构趋于复杂,部件数量增多,尺度增大引起柔性效应愈加显著;另一方面对在轨展开与控制的精度要求愈加严苛,这就需要对太空望远镜桁架的展开过程建立更加准确和高效的柔性多体动力学模型,为太空望远镜结构设计与动力学控制提供更严谨与可靠的技术参考信息。
桁架各构件在展开到位时,它们之间的活动关节处铰链会发生碰撞与锁定。在以往的动力学仿真中,为了模拟铰链锁定机构的作用,通常的做法是当折叠式机构展开到位时在关节处引入一组外力或力矩来限制住原本部件间的相对运动[14-16]。这种方式适用于构件数量较少的展开机构。在选取合理的刚度阻尼系数的情况下,如果积分步长足够小,可以获得较精确的动力学响应和接触瞬间的接触力等未知量。然而对于一些物体数量庞大、铰链多、长时间大范围运动的多体系统而言,比如本文的研究对象太空望远镜系统,三根桁架共包含上千个构件与活动关节;如果通过施加力矩模拟铰链锁定机构,随着桁架的展开,施加的力矩会一直存在且数量变得越来越庞大,这会使得后续的动力学数值仿真计算量不断增大甚至导致计算失败。因此,有必要提出一种有效的变拓扑问题的计算方法。
为了提高太空望远镜桁架展开过程的仿真精度,本文考虑了桁架各部件的柔性效应,用Jourdain速度变分原理建立了柔性体动力学变分方程。为了兼顾仿真效率,本文基于单向递推组集方法建立了柔性多体系统的动力学模型。针对柔性部件展开锁定时容易出现的数值计算问题,提出了在缓冲减速的基础上施加相对角约束的变拓扑方法。在此基础上分别对11节和30节桁架单元的太空望远镜桁架展开和锁定过程进行数值仿真,分析柔性变形对动力学特性的影响。
1 可展桁架系统结构
1.1 系统描述
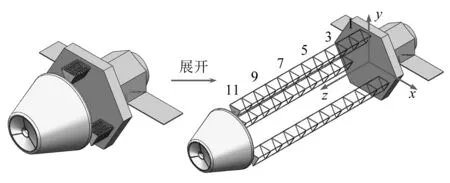
太空望远镜可展桁架多体系统如图1所示。系统主要由星体、三根对称分布式可展桁架及主镜等部件组成,其中每根桁架含有30节桁架单元,桁架与主镜各构件之间通过铰链相互铰接而成。处于折叠状态的可展桁架和主镜等部件组成的多体系统,通过三根桁架同步并行展开,推动主镜到达预定位置,然后主镜展开。桁架展开后长度达到将近38 m,其展开过程中与星体、主镜相互耦合表现出复杂的动力学特性,因此本文主要研究桁架展开动力学,在桁架展开过程中,星体与主镜始终处于收缩状态。
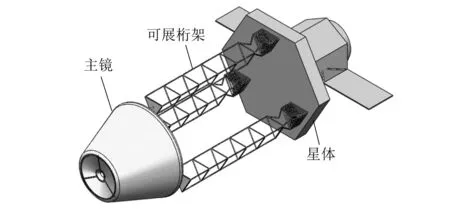
图1 可展桁架多体系统
1.2 丝杠驱动展开机构
如图2所示,可展桁架主要由三角框、折叠臂、丝杠驱动组件等构成[17],三角框与折叠臂之间以及折叠臂与折叠臂之间都采用旋转铰铰接并装有锁紧机构,三角框节点外侧安装一组滚柱与限位弹簧片。处于折叠状态的桁架在丝杠驱动作用下逐渐展开,驱动原理是:当三角框节点处滚柱滑入丝杠时,丝杠在电机作用下同步匀速旋转将旋转运动转化为三角框的匀速直线运动;当三角框运动到丝杠末端时桁架单元展开到位,同时各旋转铰关节处锁定装置作用实现瞬间锁定,并释放后一三角框滚柱进入丝杠,由此交替进行实现桁架单元逐节展开;当三角框脱离丝杠时,将由后续三角框推着往前伸展。三角框节点处限位弹簧片的作用是防止桁架单元展开过程中单元前、后端三角框滚柱同时滑入丝杠导致桁架单元展开失败。
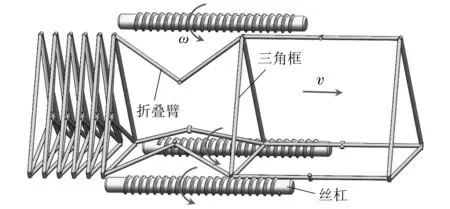
图2 桁架展开过程
本文通过在即将展开的三角框三个节点处同时施加匀速速度驱动与滑移铰来模拟丝杠驱动的作用,当桁架单元前端三角框的三个节点的外侧滚珠在驱动作用下匀速运动时,通过对后端三角框的三个节点的外侧施加点面约束模拟限位弹簧片的作用。前端三角框和后端三角框在三个节点的内侧通过旋转铰与折叠臂连接。当桁架单元展开到位时立即锁定,同时立即释放相应速度驱动与滑移铰并激活后端三角框相应速度驱动与滑移铰。由此交替进行模拟桁架单元逐节展开与延伸。
1.3 锁定机构
各构件之间的活动关节处铰链锁定机构实际中是一个复杂而精密的机械装置。为了模拟铰链锁定机构的作用:一种做法是当折叠式机构展开到位时在关节处引入一组力矩来限制住原本部件间的相对运动,但是力矩的大小与刚度系数和阻尼系数相关,较大的刚度系数会导致积分步长很小,如果锁定之后仍然施加力矩,会影响积分效率;另一种做法是基于变拓扑多体系统的处理方法[18],在桁架展开过程中,当各桁架单元展开到位时通过将转动铰替换为固定铰实现桁架单元的瞬间锁定。这种方法的优势是实现了桁架展开过程中的变拓扑,不需要施加与刚度系数和阻尼系数相关的力矩,因此积分步长不受影响,可以提升计算效率,主要适用于刚体系的变拓扑问题。对于柔性体系统,瞬间施加约束方程容易引起速度突变,导致弹性变形剧增。
本文将两种方法有效地结合起来,在锁定之前,采用在铰链处施加与缓冲器等价力矩的方法,力矩大小参考动力学仿真软件ADAMS阶跃函数和双侧碰撞函数[19]
M=STEP(θ,θ1,0,θ2,1)×
(1)
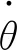
当转动铰的相对角速度趋于零时,在铰点处施加相对角约束,使转动铰转变为固定铰。由于增加了缓冲段,不会发生速度突变引起弹性变形剧增;此外,在锁定之后,由于转动铰变为固定铰,与刚度系数和阻尼系数相关的力矩可以瞬间释放,积分步长不需要始终保持很小,从而可以提高计算效率。
2 可展桁架多体系统动力学建模
本文着重研究桁架展开时的柔性效应以及与星体、主镜的耦合动力学特性,桁架的三角框、折叠臂等所有构件按实际柔性体建模,而星体和主镜分别作为一整体简化处理。考虑到采用笛卡尔方法描述系统位形会使系统动力学方程维数远大于系统自由度数,动力学微分方程的系数矩阵的构造过程十分复杂[20],给数值计算带来较大困难。本文采用拉格朗日坐标和模态坐标描述系统位形,基于柔性多体系统动力学的单向递推组集方法建立太空望远镜系统动力学模型。
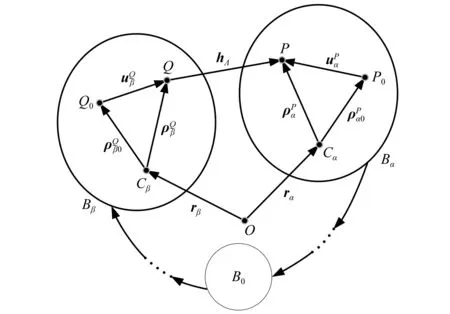
2.1 邻接物体运动学递推关系
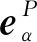
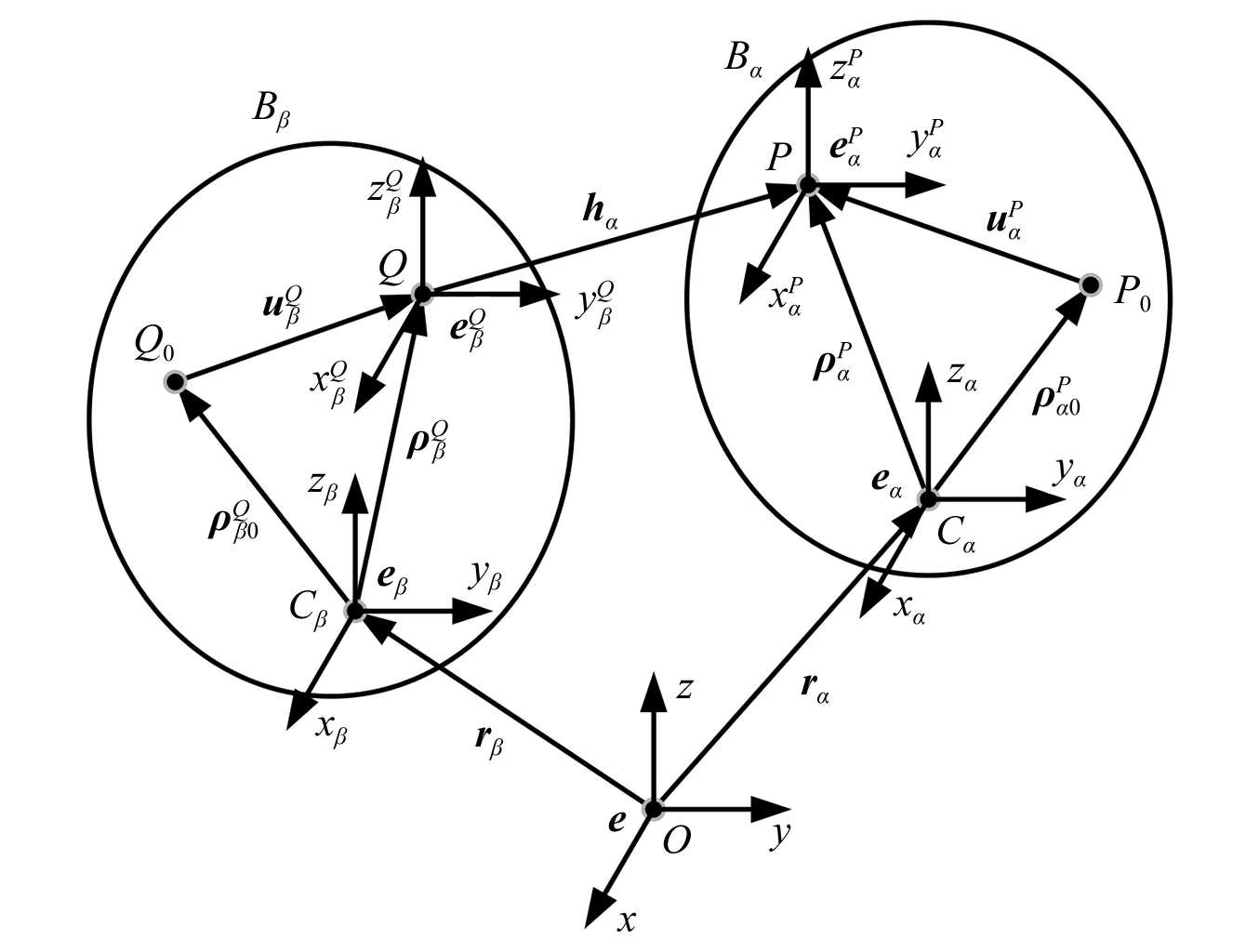
图3 邻接物体的几何关系
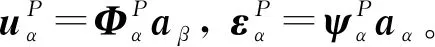
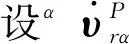
(2)
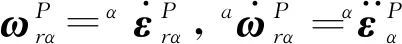
(3)
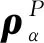
(4)
(5)
相应的绝对坐标关系式为
(6)
(7)
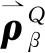
(8)
(9)
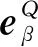
(10)
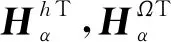
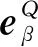
(11)
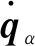
对于矢量hα,满足以下矢量关系式
(12)
(13)
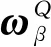
(14)
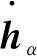
(15)
(16)
由图3可知,相邻两物体浮动坐标系的角速度满足以下矢量关系式
(17)
由式(3)和式(10),上式在绝对坐标系下的关系式为
(18)
相邻两物体浮动坐标系的角加速度满足以下矢量关系式
(19)
由式(3)和式(10),上式在绝对坐标系下的关系式为
(20)
其中,
(21)
矢径rα和rβ满足
(22)
其绝对坐标式为
(23)
对式(22)求导,并联立式(6)~式(9)、式(15)、式(16),得相应的速度与加速度绝对坐标关系式分别为
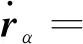
(24)
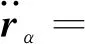
(25)
其中,
(26)
定义
(27)
将式(18)、式(20)、式(24)和式(25)合并为以下形式
(28)
(29)
其中,
(30)
(31)
由此,得到相邻两物体之间速度与加速度的递推关系式。
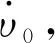
(32)
(33)
其中,
S00=I(6+S),Sα0=JαβSβ0(β=L(α);α=1,…,N)
(34)
(35)
(36)
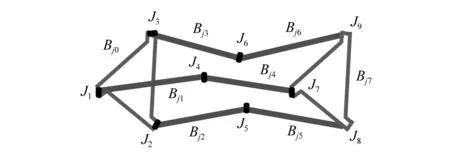
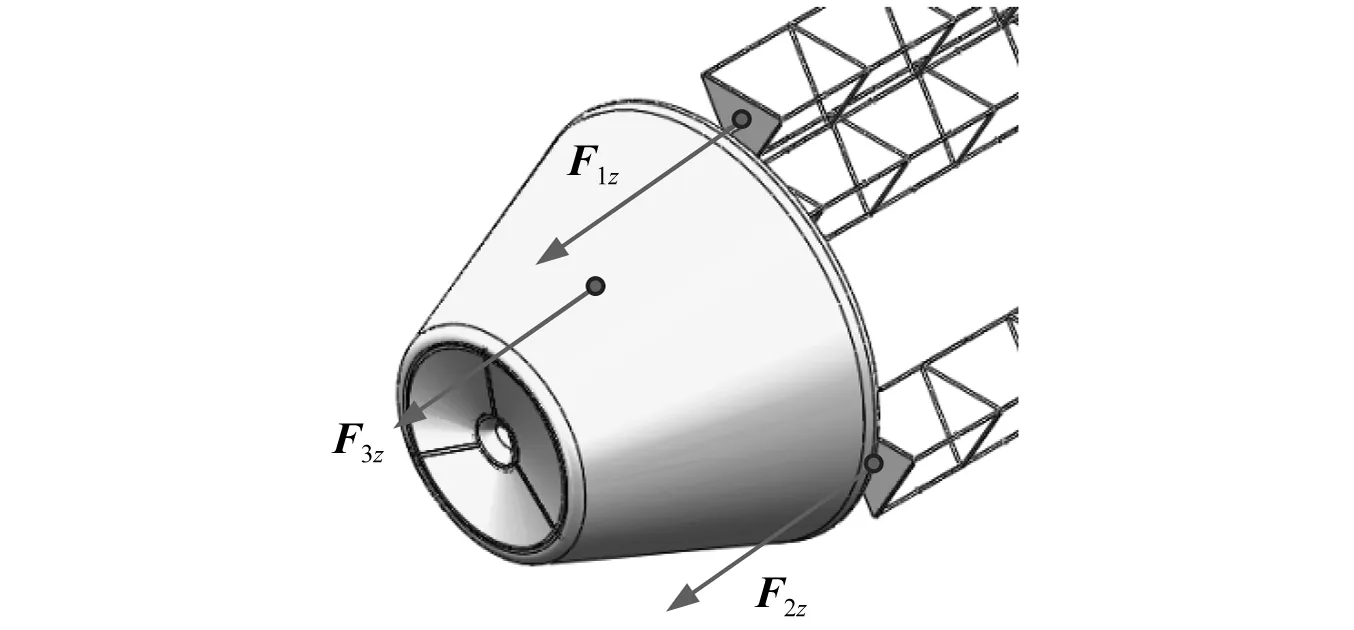
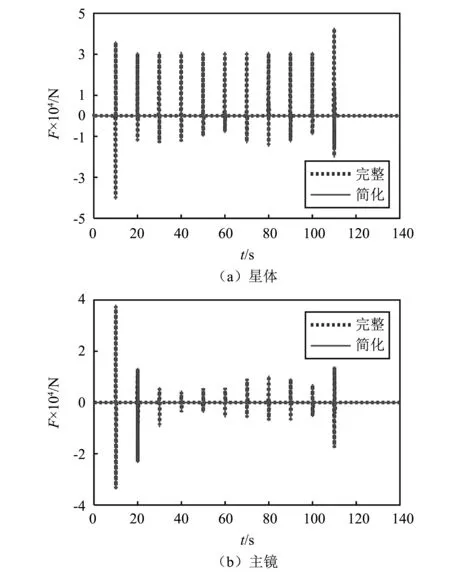
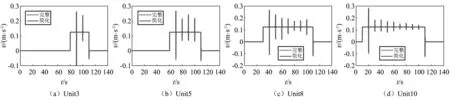
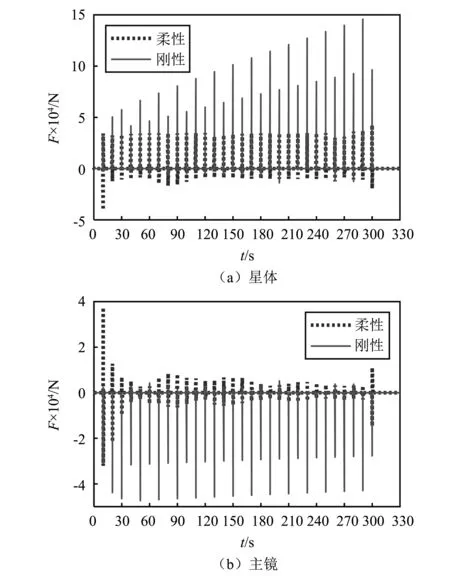
式中:Bi 将系统N个物体的矩阵关系式(32)与式(33)分别合并为以下形式 (37) (38) 其中, (39) (40) 对于单个物体Bi,根据速度变分原理,其变分形式的动力学方程为 (41) (42) 式中,Fe为系统内物体间相互作用的力元。 定义柔性多体系统的质量阵和力阵分别为 (43) 将式(37)、式(38)、式(43)代入式(42)得 (44) 由于本文研究对象太空望远镜系统是一个闭环系统,不能直接应用式(44),处理方法是选择性地切断一些铰链把系统转化为派生树系统,同时针对切断铰引入相应的独立约束方程,下面推导切断铰的约束方程。 如图4所示,考虑系统中某切断铰hΛ,当受到铰链的约束时,两物体相对运动受一定限制,应满足如下一般形式的约束方程组 图4 含切断铰邻接物体几何关系 TΛ(rα,Aα,aα,rβ,Aβ,aβ,t)=0 (45) 式中,Aα与Aβ分别为物体Bα和Bβ浮动坐标系相对绝对参考系的方向余弦阵。 对式(45)分别求一阶和二阶导数得到如下形式的速度与加速度约束方程 (46) (47) 其中, (48) (49) (50) 对于有l个切断铰的闭环系统,其约束方程、速度约束方程及加速度约束方程分别为 (51) 引入拉格朗日乘子μ,第一类拉格朗日方程为 (52) 将派生树系统动力学方程式(44)与切断铰约束方程式(51)组集即为系统的动力学方程 (53) 对于变拓扑柔性多体系统,设TL=(p,t)=0为附加相对角约束方程,对应的速度和加速度约束方程为 (54) 系统的动力学方程为 (55) 式中,μL和ξL分别为与附加约束方程相对应的拉格朗日乘子列阵和加速度约束方程的右项。 在用单向递推组集方法建立太空望远镜系统动力学模型的基础上,本节对图5所示太空望远镜桁架展开和锁定过程进行动力学仿真。首先以图5中的每根桁架含11节桁架单元的模型为对象,进行数值仿真和动力学分析;然后将多体动力学建模拓展到实际含30节桁架单元太空望远镜系统进行桁架展开与锁定动力学数值分析。系统各构件物理参数如表1所示,其中三角框和折叠臂均为铝合金6061材质,弹性模量为70 GPa,体密度为2 700 kg/m3,丝杠驱动展开速度设为0.124 5 m/s。当桁架展开时,为了模拟星体在控制器作用下处于静止状态,本文将星体固定。绝对参考系x,y和z方向和各桁架单元编号如图5所示。 表1 系统物理参数 图5 太空衍射望远镜系统 图6所示为第j个桁架单元。转动铰J1,J2和J3的铰坐标分别为柔性梁Bj1,Bj2,Bj3相对于三角框Bj0的姿态角qj1,qj2,qj3;转动铰J4,J5和J6的铰坐标分别为柔性梁Bj4,Bj5,Bj6相对于Bj1,Bj2,Bj3的姿态角qj4,qj5,qj6;转动铰J7,J8和J9的铰坐标分别为为三角框Bj7相对于柔性梁Bj4,Bj5,Bj6的姿态角为qj7,qj8,qj9。 图6 桁架单元 图7 主镜纵向受力 本文首先基于上述多体动力学理论对含11节桁架单元的1/3系统简化模型进行动力学建模与数值仿真,然后,为了验证简化模型的准确性,对每根桁架含11节桁架单元的完整系统模型进行动力学仿真,将二者动力学仿真结果进行对比。两种模型的桁架展开最后锁定时间均为110 s ,总仿真时间取140 s。 通过数值仿真得到桁架展开过程中对星体与主镜的z方向冲击力-时间曲线如图8所示。其中,为满足数值上的可比性,已将1/3系统简化模型计算求得z方向冲击力扩大3倍。通过对比1/3系统简化模型与完整系统模型,发现在桁架展开过程中,两种模型对星体与主镜产生的沿z方向的冲击力时间曲线基本重合。 图8 11节桁架单元对星体与主镜z方向冲击力 图9所示为桁架展开过程中桁架单元编号分别为3,5,8,10相对应的前端三角框质心沿z方向的速度时间曲线。通过对比1/3系统简化模型与完整系统模型,可以发现在各桁架单元展开过程中,两种模型相应的三角框质心速度时间曲线基本重合。 图9 11节桁架单元展开过程各三角框质心z方向速度 通过对比1/3系统简化模型数值仿真与完整系统模型动力学仿真结果,发现桁架展开过程中对星体和主镜的z方向冲击力时间曲线,以及各三角框质心z方向速度时间曲线基本一致,从而验证了本文单向递推组集建模方法的正确性和1/3系统简化模型的有效性,因此,1/3系统简化模型可用于完整太空望远镜系统桁架展开动力学仿真和分析。1/3系统简化模型的特点是计算规模小,计算效率较高,对11节桁架单元系统,其计算时间约为完整系统的1/6;对于桁架单元更多的系统,其计算效率高的优势更加明显。 为了进一步在保证求解精度与提高求解效率的前提下对实际30节桁架单元太空望远镜系统的桁架展开动力学特性进行分析,本文将1/3系统简化模型桁架展开动力学分析拓展到实际30节桁架单元,桁架展开最后锁定时间为300 s ,总仿真时间取330 s。同时,为突出柔性桁架展开过程中产生的柔性效应,本文还对刚性桁架模型进行了展开动力学数值仿真,将柔性桁架模型与刚性桁架模型展开动力学结果进行对比与分析。 图10(a)所示为30节桁架单元展开过程中对星体z方向冲击力时间曲线。从图中可以看出,实际柔性桁架在展开过程中主要在各桁架单元锁定瞬间会对星体产生冲击振荡,且每次冲击振荡的振幅相近。而刚性桁架对星体产生的冲击力则呈现出节拍性规律,随桁架单元奇、偶数相间分布、错落有致,且奇、偶数桁架单元产生的冲击力都分别随着已展开桁架单元数量的增多逐渐增大,较实际柔性桁架大得多。由于柔性桁架的一部分动能转变为应变能,因此柔性桁架对星体产生的冲击力较小。由于动能在之前桁架展开过程中已基本消耗,柔性与刚性桁架展开结束之后对星体冲击力均为0。 图10(b)所示为30节桁架单元展开过程中对主镜冲击力时间曲线,可以看出,实际柔性桁架在展开过程中对主镜产生了冲击波;冲击力幅度波动起伏,变化较大,整体按正弦规律逐渐衰减,冲击幅度较小。刚性桁架对主镜产生的冲击力幅度同样呈现出节拍性规律,随桁架单元奇、偶数相间分布、错落有致;与对星体冲击不同的是,对主镜的冲击整体来说较均匀,偶数桁架单元相对奇数桁架单元产生的冲击要小,且奇、偶数桁架单元产生的冲击分别整体大致恒定,但比实际柔性桁架要大得多。桁架展开结束之后对主镜冲击力都为0。 图10 30节桁架单元对星体与主镜z方向冲击力 图11所示为30节桁架单元展开过程中,桁架单元编号分别为5,10,15,20,25,30相对应的前端三角框质心沿z方向的速度时间曲线。可以看出,实际柔性桁架已展开桁架单元各三角框质心沿z方向的速度在桁架继续展开过程中基本保持恒定,但在各桁架单元锁定时速度会出现一定往复变化,呈现出的是已展桁架在后续桁架单元锁定瞬时产生了伸缩变形;每次速度变化幅值都不一样,反映出已展桁架每次出现的伸缩变形程度不同。而刚性桁架各三角框质心速度时间曲线则几乎呈理想状态,各桁架单元只要展开锁定之后,相应三角框质心沿桁架展开方向的速度则一直保持恒定,直至桁架最后锁定,这是因为刚性桁架在展开过程中没有伸缩变形。柔性与刚性桁架展开结束之后三角框质心速度都为0,这也恰好能解释在桁架展开结束之后,桁架对星体与主镜的冲击力基本为0。 图11 30节桁架单元展开过程各三角框质心z方向速度 本文对太空望远镜桁架展开和锁定的动力学建模方法进行研究。为了缩减系统的广义坐标数,取铰的相对坐标为系统的广义坐标,用单向递推组集方法建立了太空望远镜大型在桁架展开过程的刚-柔耦合动力学模型。针对柔性部件展开锁定时容易出现的数值计算问题,提出了先缓冲减速再附加相对角约束的变拓扑问题的处理方法。在此基础上利用系统结构对称性取1/3简化模型进一步缩减计算规模,实现了结构复杂、计算规模庞大的太空望远镜桁架展开和锁定过程的数值仿真,这种简化方法可以有效缩减计算规模,并且具有较高的精度。动力学分析结果表明,太空望远镜桁架展开的柔性效应不可忽略,将桁架简化为刚体模型会与实际动力学特性产生较大偏差;探讨了桁架展开过程中与星体、主镜的耦合动力学特性,分析了桁架展开对星体与主镜的冲击力变化规律。本文对太空望远镜桁架展开的模型简化方法与动力学数值分析结果,对太空望远镜多体系统的结构设计和动力学控制具有一定的理论参考价值与工程指导意义。2.2 柔性多体系统动力学方程
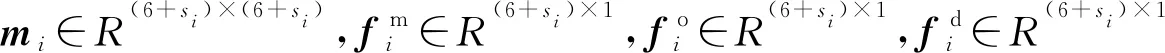
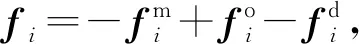
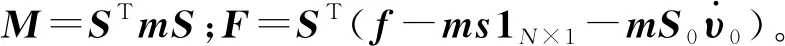
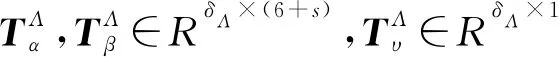
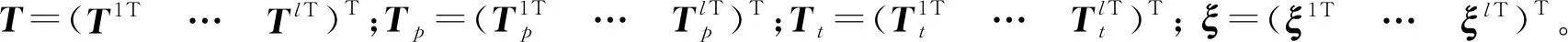
3 数值仿真
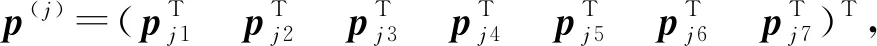

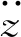
3.1 系统简化模型桁架展开动力学验证
3.2 桁架展开动力学仿真结果分析

4 结 论
