地震次生火灾中城市地铁地下结构的灾变性能研究

李文婷， 陈清军

(1.上海师范大学 建筑工程学院，上海 201418； 2. 同济大学 土木工程防灾国家重点实验室，上海 200092)

地震是一种危害巨大的自然灾害，1995年日本阪神地震中大开地铁车站严重破坏，引起各国学者对地下结构抗震的广泛重视[1-3]。然而，地震除造成直接破坏外，还可能引发次生火灾，带来更大损失。1906年美国旧金山8.3级地震中，80%的人员伤亡和建筑物损毁源自震后持续三天的火灾[4]；1923年日本东京7.9级地震造成14万人丧生，约45万间房屋被毁，其中次生火灾损失约占77%。除此之外，1994年美国加利福尼亚州北岭大地震引发次生火灾30～50起、1995年日本神户大地震引发次生火灾142起、1999年我国台湾省集集大地震引发次生火灾161起[5-6]。大量地上结构的震害和研究表明，地震次生火灾会加剧结构破坏，甚至引起建筑倒塌[7-8]，如日本福井信托银行在震后火灾中倒塌。

我国正处在“新型城镇化”战略实施的关键阶段，地下轨道交通是当前和未来一个时期大中型城市基础建设的重要内容。遭受地震破坏后，地铁车站还可能承受火灾等次生灾害的冲击。然而，由于地下结构的建设起步较晚，目前关于地下结构在地震与火灾耦合作用下灾变性能的研究比较少。地下轨道交通作为重要生命线系统，一旦在强震或震后火灾中破坏，损失重大，震后救援和修复也极为困难[9-10]。不仅如此，地下结构火灾具有空间封闭、蔓延快、灭火难的特点，如2003年韩国大邱发生的地铁纵火事件，造成198人死亡，146人受伤。因此，有必要单独研究震后火灾中地下结构的灾变行为。

目前关于地震次生火灾的研究多集中于地上结构[11]，而对地下结构的研究较少。地下结构受到周围土体作用，其地震破坏机理与地上结构存在较大不同；在震后火灾中的灾变行为也可能与地上结构存在较大不同。对于地上结构，陈适才等将结构地震损伤与热传导分析、热力分析相结合，认为在地震中已损伤的结构，其火灾破坏形态会发生改变；Vitorino等[12]通过数值仿真，认为地震作用使钢筋混凝土结构耐火性能下降；苗吉军等[13]研究震后火灾环境下混凝土结构的反应，认为损伤后混凝土材料的热传导性能提高，相应截面所经历的最高温度也增高；框架结构的高温变形恢复能力变差，梁截面承载力下降幅度比柱截面大。对于地下结构，陈阳等[14]研究了火灾后CFRP加固下地铁车站结构的地震反应；菅秀松等[15]通过构件耐火性能分析，提出钢筋混凝土梁、板、柱的合理保护层厚度。然而，现有研究多集中于单独的抗震、抗火研究，而对地震与火灾耦合作用下地下结构的破坏机理研究较少，亟需进行深入探讨，阐明地下结构在地震与火灾耦合作用下的灾变机理，为地下结构的抗震抗火设计提供参考。

本文针对典型单层双跨地铁车站结构，通过三维精细化非线性有限元数值模拟，将动力时程分析、热传导分析和热力分析相结合，讨论了地铁车站结构在地震及其次生火灾作用下的变形、损伤及内力演化，揭示了地铁车站结构在地震及其次生火灾作用下的灾变性能。

1 计算模型

1.1 地铁车站及场地参数

单层双跨钢筋混凝土结构是目前我国城市地铁地下车站结构普遍采用的结构形式，因此，本文以一个单层双跨钢筋混凝土地下结构为研究对象。该地铁车站结构的总宽17.0 m，总高7.17 m，车站中柱尺寸为0.4 m×1.0 m，中柱的纵向间距为3.5 m，车站侧墙厚0.7 m，顶板厚0.8 m，底板厚0.85 m。地铁车站结构的构件尺寸详如图 1(a)所示，配筋方案如图 1(b)所示。结构混凝土为C30，泊松比为0.18，密度为2 450 kg/m3。纵筋为HRB335，泊松比为0.3，密度为7 800 kg/m3。

车站所在场地简化为水平成层场地，共计7层，主要由全新世砂土和更新世黏土组成，总厚34 m，各土层分布及参数详见图 1(c)和表1。地铁车站结构上表面距地表4.8 m，结构大部分位于第三、第四土层，少部分位于第二、第五土层。

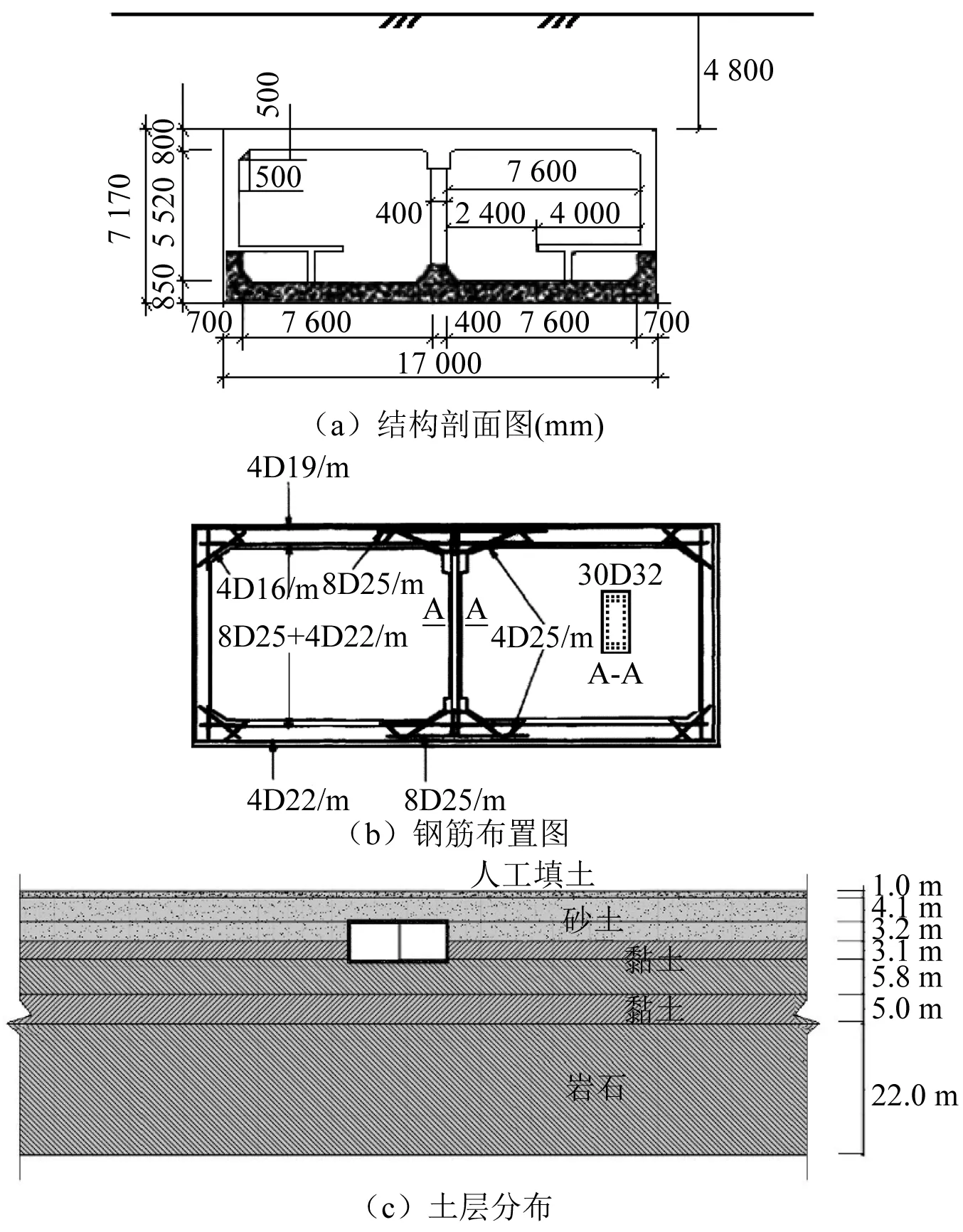
图1 结构模型

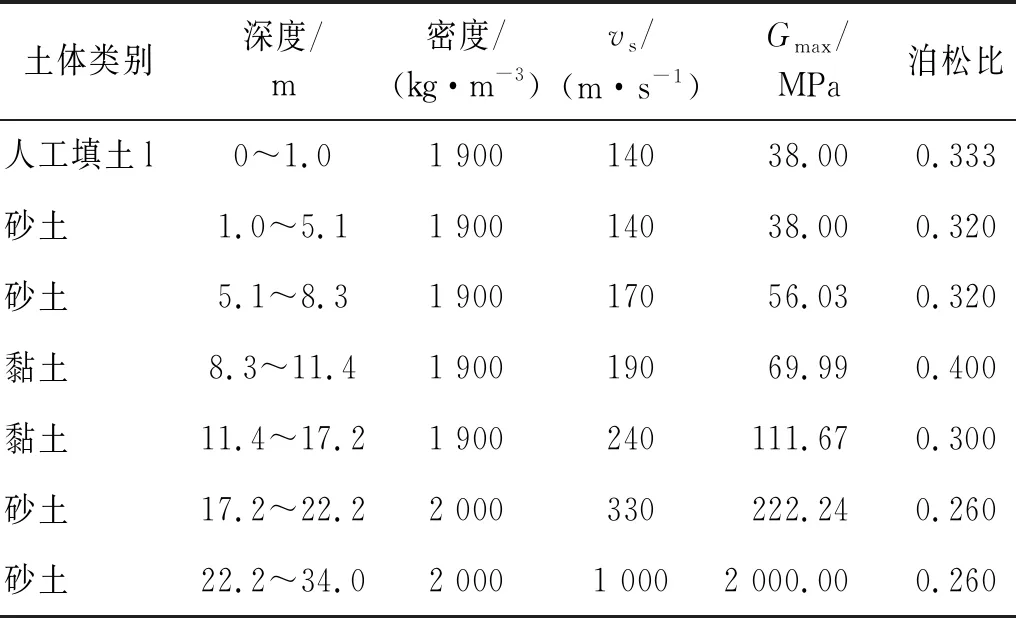
表1 场地土层参数

1.2 有限元模型建立

为模拟混凝土和钢筋在地震与火灾中的力学行为，采用混凝土与钢筋分离式建模方法，借助Abaqus软件建立如图2所示的地铁地下结构三维有限元模型，共有单元数量138 756个。

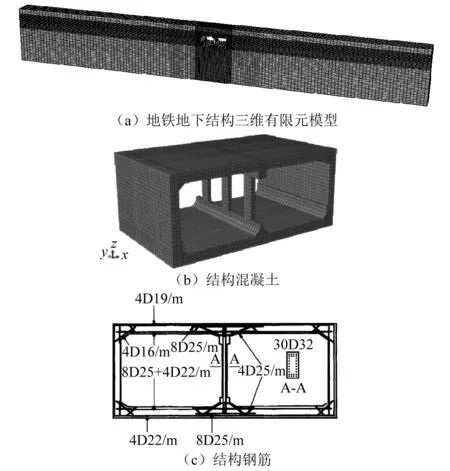
图2 有限元模型

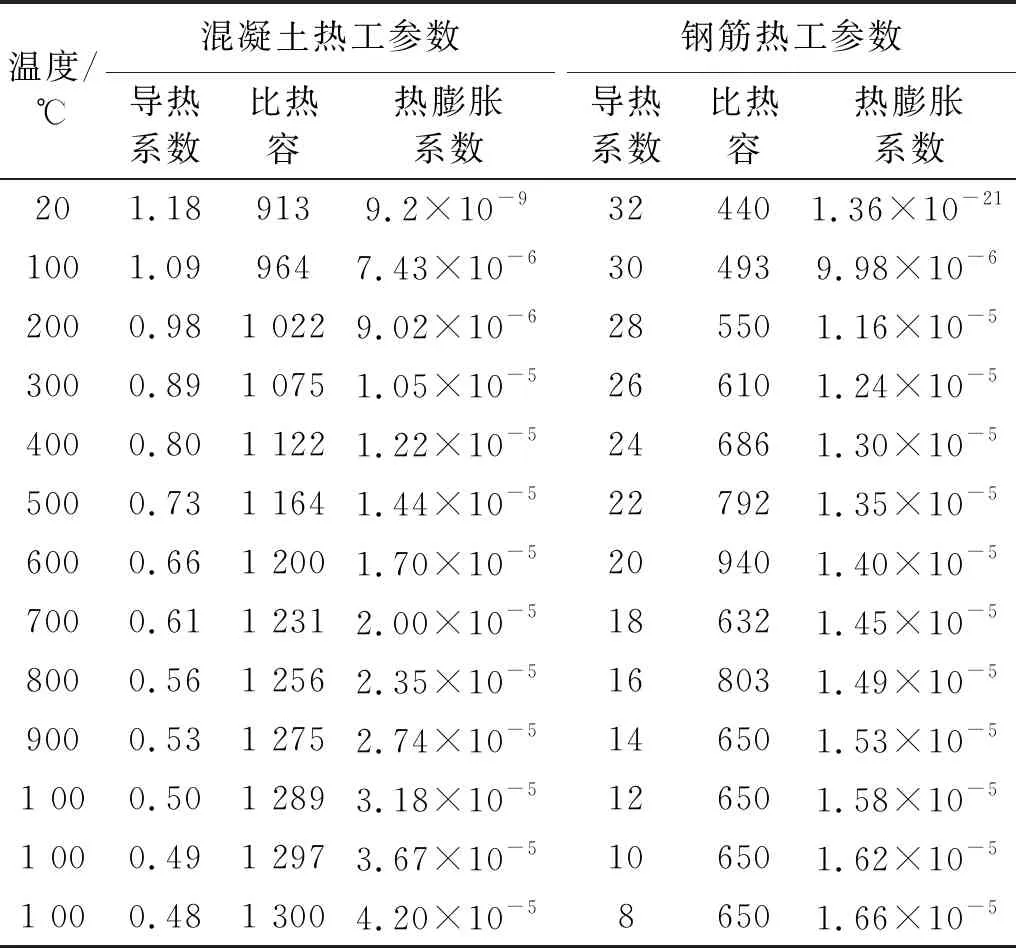
表2 混凝土及钢筋的热工参数

(1)

(2)

(3)

土体单元尺寸划分采用土体剪切波长为控制因素，最小土体单元边长为0.3 m；远置侧向边界以控制土体侧向边界对结构地震反应的影响；车站与土体之间接触面的法向行为采用“硬”接触，切向行为采用摩擦模型，摩擦因数取0.4。参数设置详见文献[17]。

1.3 荷载工况

分析中首先施加重力荷载，然后施加地震荷载，在地震波激励结束后使结构自由振动至停止；随后，继承震后结构的受力状态、变形状态和材料损伤，对结构施加温度场，进行热力分析，模拟结构在震后火灾中的灾变行为。另外，作为对比，进行了考虑重力荷载时结构的抗震性能分析，以及考虑重力荷载时结构的抗火性能分析。

地震荷载由模型底部(即基岩面)以剪切波的形式沿结构横向输入。选取1995年日本阪神地震中神户大学观测点获得的实测基岩波KBU作为输入地震波，该场地的平均剪切波速Vs30为1 043 m/s，故直接作为基岩波输入。地震动时程及傅里叶幅值谱见图 3，该波卓越频率为0.830 Hz，持时30 s。对地震波进行调幅，使输入地震动加速度峰值为3 m/s2。研究中，计算0～40 s的结构地震反应，将40 s时刻的结构变形作为结构震后残余变形，并将该时刻的结构状态作为发生火灾的初始状态。

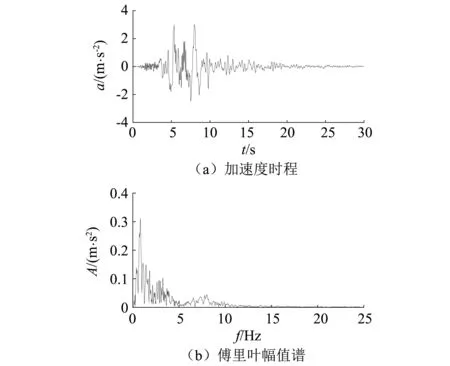
图3 输入地震动

火灾分析中，采用ISO-834升温曲线(见图 4)，模拟车站左侧车厢着火场景。火灾发生前的环境温度为20 ℃，火灾持续时间共计2 h，最高温度为1 049 ℃。地震、火灾及重力荷载如图5所示。

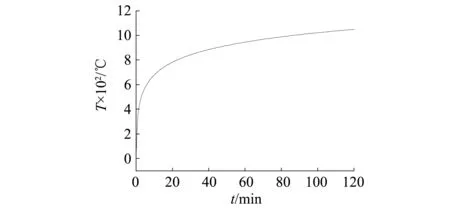
图4 ISO-834升温曲线

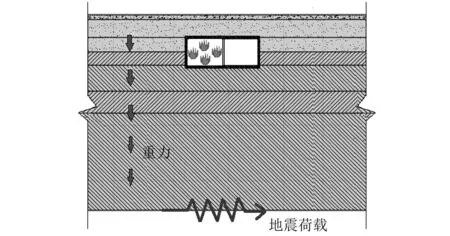
图5 荷载示意图

采用Rayleigh阻尼模型建立阻尼矩阵。已有研究表明，Rayleigh 比例阻尼矩阵不同建模方式对土层加速度反应计算结果影响很大，本研究参考文献[18]，Rayleigh 阻尼矩阵比例系数计算公式中的第一个自振频率ωm取土-结构相互作用体系的第一阶自振圆频率；第二个自振频率ωn取值方法如下：当土层基频高于基岩地震波的主要分量激励频率时，ωn取土层第二阶自振圆频率；当土层基频等于或低于基岩地震波的主要分量激励频率时，ωn取输入基岩地震波反应谱的峰值圆频率。

2 有限元模型合理性验证

结构在地震作用下的变形可以从整体上反映了地铁车站结构的地震响应特征。本模型中地铁车站结构在强震作用下的典型变形如图6所示，呈倾斜的“M”形。Yoshida等[19]在1996年针对在1995年日本阪神地震中发生严重破坏的大开地铁车站展开了详细的震害调查，杜修力等[20]归纳总结了大开车站震害事例的分析方法、分析模型及相应结论。在大开地铁车站破坏最严重的区域，几乎所有的柱子都完全倒塌，车站的顶板发生下落，车站在地震之后变为了倾斜的“M”形，且主要破坏部位为中柱底部、侧墙上侧和顶板，如图7所示[21]，与本文模拟成果相符。

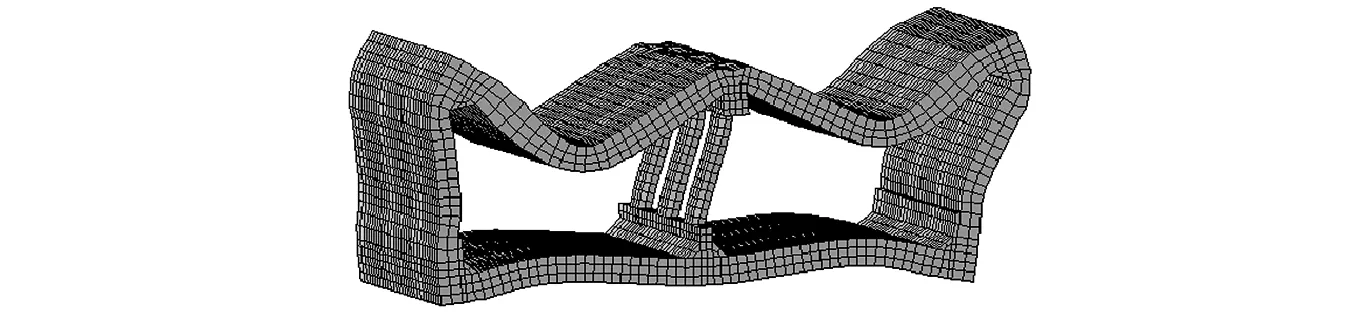
图6 地铁车站结构在强震作用下的典型变形

图7 Yoshida等对大开地铁车站破坏状态的描述

取Abaqus模拟结果中距离地铁车站结构和人工边界均较远的场地反应作为自由场反应，与Shake 91求解结果对比，结果详见Li等的研究。总之，Abaqus模拟结果与Shake 91软件分析求得的土层最大剪应力和最大剪应变有所差别，但差别不大；由两种方法求得的地表加速度响应在时域和频域内均可以很好吻合。

土体计算范围和人工边界将直接影响土-结构相互作用问题模拟结果。比较当侧向人工边界与地铁车站距离分别取80 m，132 m和200 m时结构应力反应和加速度反应，认为当侧向人工边界与地铁车站结构之间的距离取132 m时，人工边界处的反射波几乎不会传播至结构及周围土体。另外，地震作用下土-地铁车站结构相互作用体系的加速度分布，如图8所示，可见，在距离地铁车站结构和人工边界均较远的区域，土体加速度响应水平成层分布，满足自由场响应规律。故而，本模拟可很好消除土体有限域化对结构地震反应的影响。

图8 地震作用下土-结构相互作用体系的加速度反应

考虑计算的时间成本，本文有限元模型中仅建立了地铁车站结构的三跨模型，这就不可避免得引入平行于结构横截面方向的两个侧向边界的干扰。为评估两个侧向边界的干扰范围和程度，沿结构侧表面不同高度选取25条水平路径，对比土压力沿水平路径的分布，对比结果详见Li等的研究。总之，两个侧向边界可能减小或增大结构侧表面土压力，但影响范围有限；综合考虑精度要求和时间成本，取地铁车站结构的三跨进行有限元分析。

3 结果分析

本文首先阐述地震作用下结构的灾变行为，然后通过与只经历火灾的地下结构对比，研究地震损伤对地下结构抗火性能的影响。

3.1 结构变形反应

3.1.1 结构整体变形

本文建立的土-地铁车站结构相互作用体系的自振频率为2.438 Hz，第一阶振型中地铁车站结构的变形以剪切变形为主，如图9所示。地震作用下，地铁车站结构的层间位移响应时程如图10所示。在地震刚发生时，地下结构的变形以整体剪切变形为主；随着地震进行，结构侧向变形逐渐增大，顶板开始变形；结构框架柱和侧墙的刚度减小；结构顶板发生严重变形，结构的竖向承载能力明显下降，最后地铁车站结构呈现倾斜的“M”形；结构层间位移最大时的结构变形如图 11所示(变形放大系数为50)。关于地铁车站结构的地震反应参见文献[22-23]，此处不再赘述。

图9 土-结构相互作用体系的第一振型

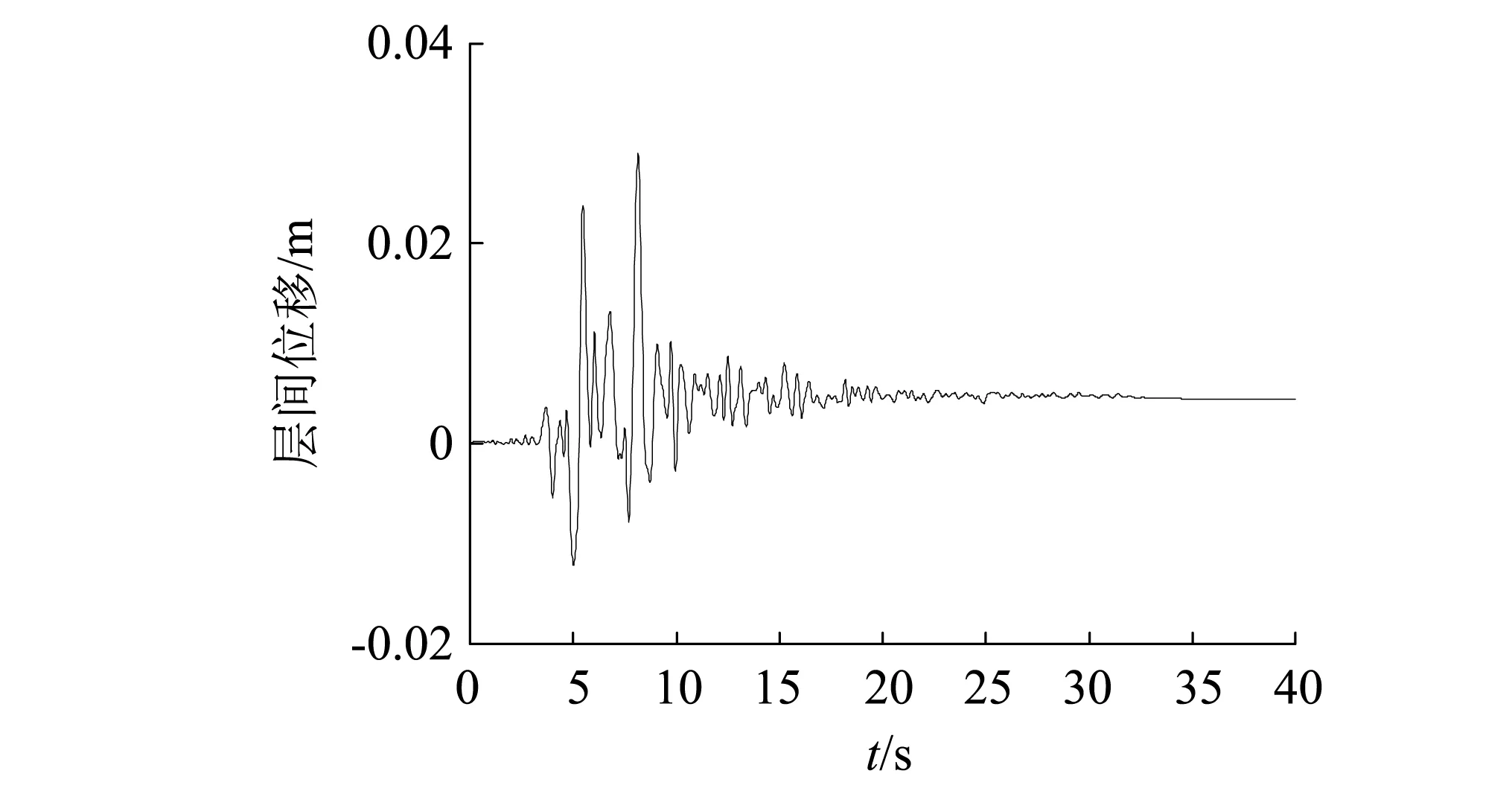
图10 地震作用下地铁车站结构的层间位移响应时程

图11 地震作用下结构变形图

火灾发生后3 min，30 min，60 min和120 min时，地下结构的变形及整体温度分布、中柱横断面的变形及温度分布0、顶底板横断面的变形及温度分布如图 12所示。可见，火灾作用下，结构中柱不再呈剪切型破坏，而是向外凸起(相对于左跨)；结构侧墙仍接近剪切变形，变形增大；结构顶板挠度增大；底板由于中柱的约束而变形不均匀、局部凸起。火灾中温度由车厢内表面向外扩散，沿构件厚度方向温度基本成层分布。中柱内侧温度高而发生膨胀，使中柱横截面不再呈矩形，而是发生弯曲变形。

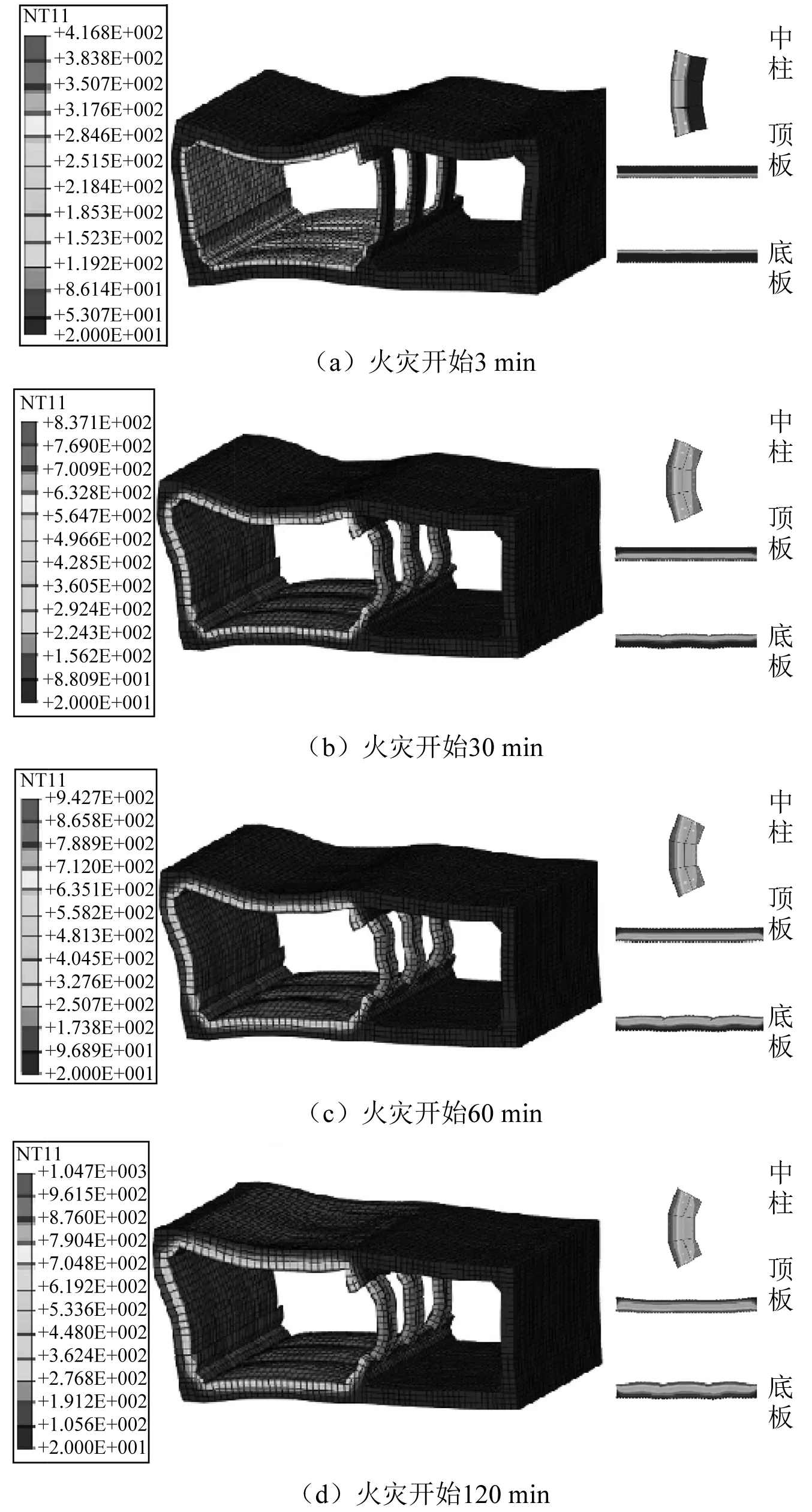
图12 火灾中地铁车站结构的变形及温度变化

随着火灾发生，结构中柱、侧墙和顶板的温度变化曲线如图13所示。可见，火灾中各构件温度先快速增大，在约20 min后减缓，略滞后于输入温度荷载。中柱的内外温差最大，在火灾2 h时达到730 ℃；而内外温差最小的构件是侧墙，在火灾2 h时为441 ℃；顶板内外温差在火灾2 h时为587 ℃。对于构件内侧升温，中柱升温最快，而侧墙与顶板的升温曲线相近；对于构件外侧升温，侧墙的升温最快，而中柱与顶板的升温曲线相近。

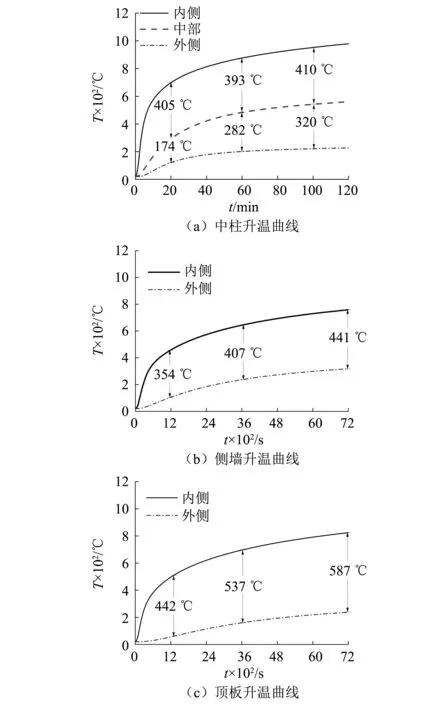
图13 火灾中地下结构各构件内外侧升温曲线

为定量研究地震及其次生火灾对结构整体变形的影响，图 14同时给出考虑结构地震损伤与不考虑结构地震损伤时，火灾中结构的层间位移反应时程。可见，震后火灾发生前，结构存在0.004 m的地震残余位移；随着火灾的发生，结构层间位移迅速增大，在火灾发生2 min时，经历过地震的结构层间位移为0.006 m，而未经历地震的结构层间位移为0.002 m；10 min之后，结构层间位移增速放缓，随时间线性增大，火灾发生2 h时，考虑地震影响的结构层间位移为0.016m，不考虑地震影响的结构层间位移为0.014 m。

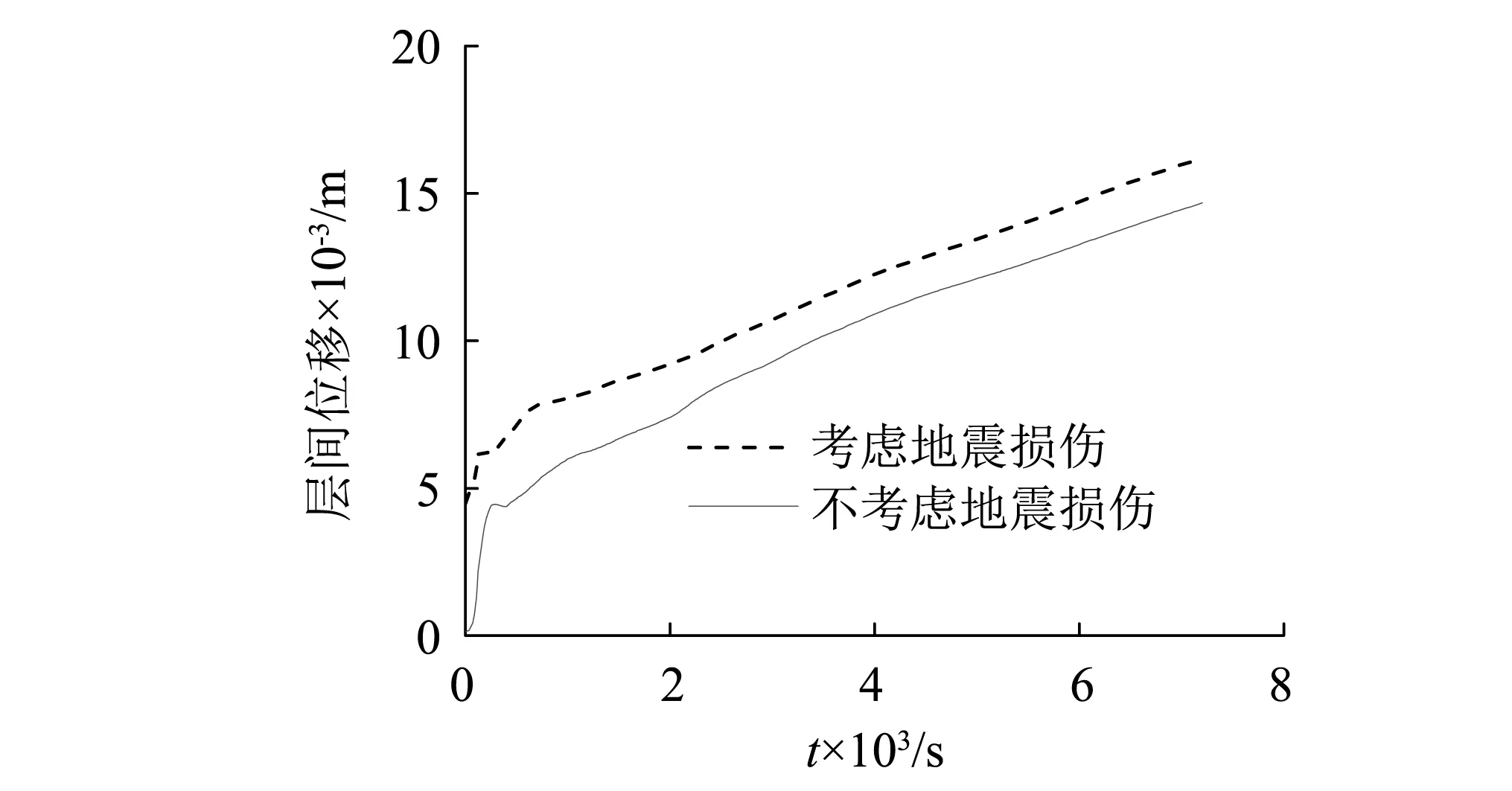
图14 火灾中结构层间位移时程

综上可见，与只经历火灾作用而不考虑地下结构在地震中的损伤相比，地震次生火灾作用中地下结构层间位移增大约0.002～0.004 m，地震破坏明显加剧了震后火灾中地下结构变形，但其影响略小于地下结构在地震中的残余变形。

3.1.2 结构中柱变形

结构中柱是可能导致地下结构倒塌的关键构件，在地震中破坏最为严重。故此，本文特别关注结构中柱在震后火灾中的灾变行为。图 15给出了结构中柱在地震与次生火灾作用下，以及火灾单独作用下的柱顶与柱底相对位移时程。可见，火灾单独作用下，随着火灾发生，结构中柱的变形迅速增大，在232 s达到最大值0.003 9 m；随后，中柱变形反向增大，在0.5 h后稳定0.000 8 m左右。当考虑结构在地震中的损伤时，火灾发生时刻中柱存在0.003 m的残余变形；随着震后火灾发生，结构中柱变形规律与不考虑地震时相似，先迅速增大，在125 s达到最大值0.004 5 m；后反向增大，在火灾发生1 h后稳定在0.002 1 m左右。

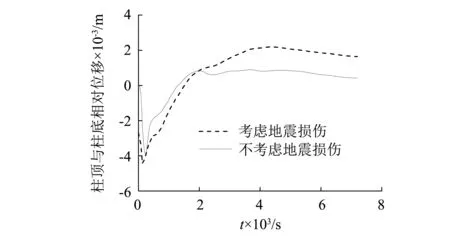
图15 火灾中中柱柱顶与柱底相对位移时程

综上可见，考虑地下结构在地震中的损伤时，火灾中结构中柱的变形增加更快、变形更大；震后火灾中结构中柱的柱顶与柱底相对位移较不考虑地震影响时明显增大，最大增幅约116%。

3.1.3 结构顶板变形

地下结构埋置于土体中，其除与地上结构一样受到自身重力荷载外，还承受上覆土体的土压力。因此，地震及火灾中地下结构顶板的受力特性可能与地上结构存在较大不同。结构顶板在地震及其次生火灾作用下，以及火灾单独作用下的顶板挠度时程如图 16所示。可见，不考虑地震荷载时，随着火灾的发生，结构顶板挠度逐渐增大，特别是在火灾发生的前7 min增长迅速，在时刻7 min时挠度达到最大0.016 m；之后，中柱挠度随着火灾发生缓慢增大，在火灾2 h时达到0.026 m。考虑地震时，结构顶板挠度的发展规律与不考虑地震时相似；地震后，结构顶板存在0.005 8 m的竖向残余变形；随着震后火灾的发生，顶板挠度在火灾发生0～7 min迅速增至0.019 m，比不考虑地震时的最大挠度0.016 m增大19%；之后，结构顶板挠度随着火灾发生缓慢增大，在0.5 h后与不考虑地震影响的结构顶板挠度之差基本可忽略。

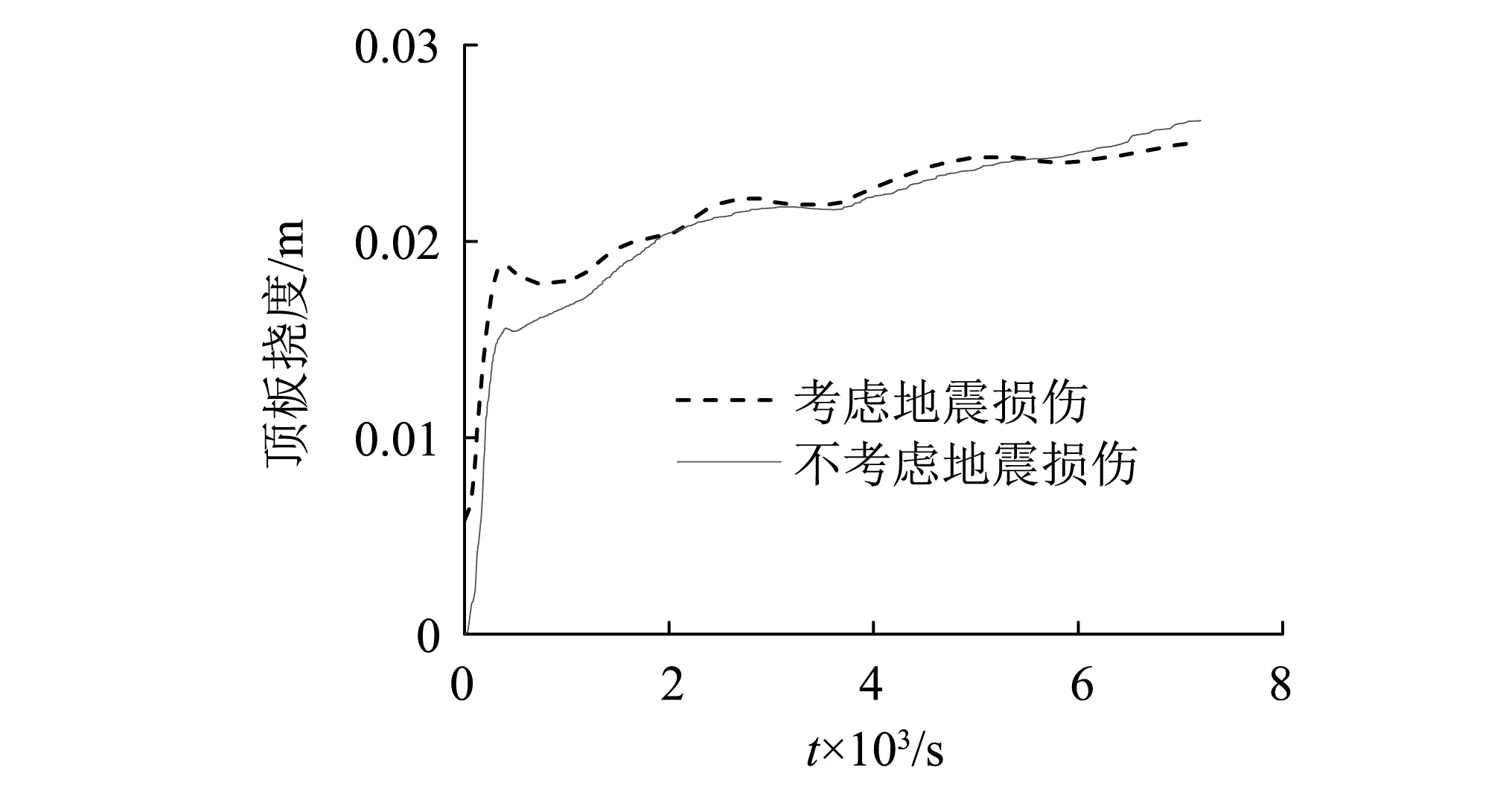
图16 火灾中结构顶板挠度时程

综上可见，考虑地下结构在地震中的损伤时，地下结构顶板挠度在火灾刚发生的前0.5 h明显大于不考虑地震影响时的结构顶板挠度，而在0.5 h之后，地震对结构顶板变形的影响可以忽略。

3.2 结构损伤及内力反应

在地震作用下，地铁车站结构发生明显破坏的部位主要集中在框架柱上下端、侧墙上下端、顶板两侧、底板两侧和框架梁与顶板的交接处。火灾作用下地铁车站结构的混凝土破坏主要集中于结构受火面，即车站内侧；钢筋破坏主要集中在结构的背火面，即车站外侧。混凝土等效塑性应变云图和钢筋Mises应力云图，如图 17所示。结构损伤在震后火灾中显著增大，较地震结束时刻，结构混凝土等效塑性应变在震后火灾0.5 h增大817%，在震后火灾2 h增大1 632%；钢筋Mises应力在震后火灾0.5 h增大28%，在震后火灾2 h增大34%。

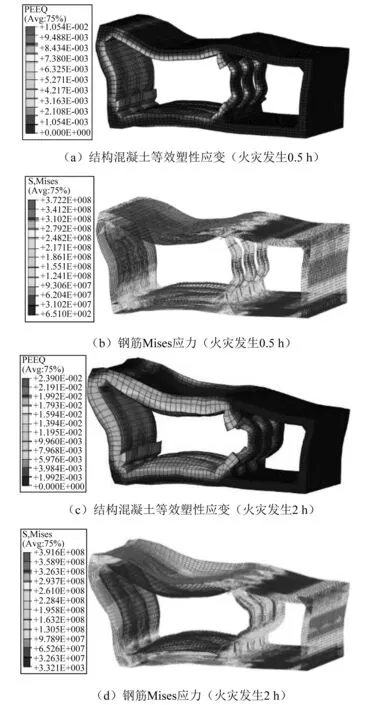
图17 火灾中结构混凝土等效塑性应变及钢筋Mises应力云图

选取地下结构5个截面(见图18)，分析结构构件内力变化。地震及其次生火灾作用以及火灾单独作用下，中柱柱顶(断面1-1)、柱中(断面2-2)、柱底(断面3-3)，以及顶板中部(断面4-4)、侧墙上部(断面5-5)的轴力、剪力及弯矩等内力时程见图 19。可见，考虑地震影响时，结构各构件的内力随时间的变化规律与火灾单独作用时比较一致，个别情况下数值差别较大。具体而言，火灾发生125 s时，中柱弯矩达到极限，随后构件承载力下降，柱顶与柱底弯矩在2 000 s后稳定在50～100 kN·m，而柱中弯矩在5 500 s时发生反向。中柱在125 s破坏后，结构发生内力重分布，顶板和侧墙的内力迅速增大，侧墙上部弯矩在150 s达到最大，随后顶板中部弯矩在180 s达到最大；之后，顶板与侧墙的弯矩迅速减小，在400 s时即达最小值，稳定在3 200 kN·m附近。对于轴力，除顶板轴力在只考虑火灾而不考虑地震的工况中出现短暂拉力外，其余构件在整个火灾过程中均处于受压状态；这与地上结构有较大不同。分析原因，认为地下结构处于土体的包围中，结构周围土体提供了有效支撑作用。中柱轴力在短暂减小后迅速增大，随后达到极限，竖向荷载向侧墙转移，侧墙轴力持续增大。中柱剪力数值较小，在结构破坏中不起控制作用；地震破坏对结构受火的初始剪力影响较大，但对火灾过程中的剪力值影响较小；中柱剪力随结构变形而发生反向。

图18 截面示意图

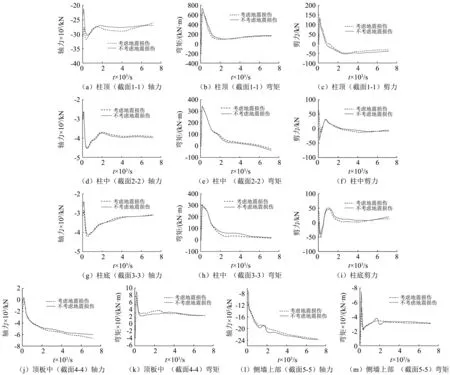
图19 火灾中结构内力反应

定量上，在地震与次生火灾作用下，以及火灾单独作用下结构构件的内力最值列于表3。可见，较只考虑火灾对地下结构的影响，考虑结构在地震中的损伤时，中柱各截面压力最值及柱底弯矩最值增大，其中以中柱柱顶轴力增大最明显，但增大幅值均在5%以内。除此之外，其余各构件承载力均下降，其中以侧墙上部弯矩变化最为明显，减小幅值约为30%；之后依次是顶板中部弯矩、中柱顶部弯矩、侧墙上部轴力、中柱中部弯矩和顶板中部轴力，减小幅值依次为13%，10%，1.3%，0.3%和0.1%。因此认为，考虑结构在地震中损伤对结构构件在火灾中的抗弯承载力影响较大，最大影响部位为结构侧墙，其抗弯承载力降幅约为30%。

表3 构件内力最值

4 结 论

本文通过对一个单层双跨地铁车站结构的三维精细化非线性数值模拟，讨论了地下结构在地震及其次生火灾作用下的变形、损伤及内力演化，阐述了地震荷载对地下结构抗火性能的影响，主要结论如下：

(1)在地震中已经发生损伤的地铁地下结构，在震后火灾中变形继续增大，损伤进一步加剧。与地震作用后结构变形相比，火灾作用下，结构中柱不再呈剪切型破坏，而是向外凸起(相对于着火跨)；结构侧墙仍接近剪切变形，变形增大；结构顶板挠度增大。

(2)地震及其次生火灾作用下，地下结构的层间位移较只考虑火灾作用时增大约0.002～0.004 m，地震破坏明显加剧了震后火灾中结构变形，但其影响略小于结构震后残余变形。

(3)地下结构的地震损伤对次生火灾中地下结构抗倒塌的关键构件-中柱-的变形影响明显。考虑地震影响时，火灾中结构中柱的变形增加更快、变形更大；中柱柱顶与柱底相对位移较不考虑地震影响时最大增幅约116%。不仅如此，结构中柱的变形在火灾发生初期增大很快，在火灾发生125 s(考虑地震)或232 s(不考虑地震)时即达到最大值。

(4)地震作用对火灾作用下结构顶板挠度的影响，主要集中在火灾发生0～0.5 h，地震及其次生火灾作用下结构顶板的最大挠度比只考虑火灾作用时结构顶板最大挠度增大19%。

(5)地震作用对火灾中地下结构各构件的内力发展规律影响不大：火灾中地下结构中柱发生受弯破坏，结构内力重分布使顶板和侧墙内力迅速增大；各构件除顶板轴力在只考虑火灾而不考虑地震的工况中出现短暂拉力外，均处于受压状态。地震作用对地下结构侧墙在火灾中的抗弯承载力削弱最大，降幅约为30%。