浅埋单层三跨地下结构在竖向地震作用下的动力响应

杨谨瑞，　戚承志，　魏小琨，　刘天添

(北京建筑大学 土木与交通工程学院 北京市高校工程结构与新材料工程研究中心， 北京　100044)



浅埋单层三跨地下结构在竖向地震作用下的动力响应

杨谨瑞，戚承志，魏小琨，刘天添

(北京建筑大学 土木与交通工程学院 北京市高校工程结构与新材料工程研究中心， 北京100044)

摘要：采用结构动力学方法，通过求解地下结构顶板的动力响应得到了单层三跨地下结构中柱在竖向地震分量作用下的动力响应. 地下结构首先被看作是刚体，利用与地基的相互作用得到地下结构在竖向地震分量作用下的动力响应. 其次，由于地下结构的对称性，取一半进行简化分析，侧墙对于顶板的约束用抗弯弹簧代替. 再次，根据边界条件将之前的刚体动力响应作为输入，可以求得顶板的剪力. 最后，通过之前求得的顶板剪力进而求得中柱的受力情况. 结果表明，竖向地震分量对中柱的作用是显著的，甚至会对地下结构中柱产生严重的破坏.

关键词：竖向地震分量； 单层三跨； 中柱； 动力响应

早期地震工程中认为，地下结构受地震的影响很小. Newmark N.M.等[1]是最早研究竖向及水平地震峰值的学者之一. 他们的研究表明，竖向地震加速度峰值可以比较安全地取为水平分量的2/3. 有记录表明，有些地震产生的竖向加速度不仅相对于水平地震分量来讲很高，而且绝对值也很大. 在地铁车站中柱发生不同程度的破坏中，观测到中柱中间部分有环向和竖向裂纹或者屈曲、被压碎. 在日本阪神地震中，大开地铁车站破坏最为严重，有一半以上中柱倒塌，这就导致了顶板的坍塌和上覆土层的大量沉降，沉降量最大的地方达2.5 m. 因为对于对称结构来讲，在水平地震动作用下，中柱中间部分的弯矩基本上为零，因此中柱中间部分的环向、竖向裂纹、屈曲与压碎破坏不能够认为是水平地震动引起的.

竖向地震分量对于地下结构的影响，相关专家学者也取得了一些成果. 姚小彬等[2]发展了一种求解浅埋地下结构顶板频率和振型的方法. 于翔等[3]通过冲量原理分析了竖向地震分量对于地铁结构破坏的影响，发现竖向地震作用的破坏也是非常大的. 李信桥等[4]采用ABAQUS软件对地下结构受竖向、横向以及横竖向地震分量共同作用下的动力响应进行了模拟. 杨春田[5]采用冲量原理计算竖向地震作用，针对日本阪神地震中柱破坏进行了定量分析,认为竖向地震动必须在地下结构的计算中考虑. 戚承志等[6]给出了一种箱形地下结构抗震计算方法. 王越等[7]认为研究竖向地震分量对于地下结构的作用主要应该针对竖向地震分量作用的定量研究. 在文献[8]中，戚承志等研究了浅埋地下结构顶板在竖向地震作用下的动力响应，但是没有研究中柱和底板的动力响应.

对于地下结构，有时竖向地震分量的作用是显著的，有时还是很严重的. 由于中柱是地下结构在地震时最薄弱的部位. 目前对于地下结构在竖向地震作用下的动力响应的研究较少，且主要集中于数值模拟，缺乏理论模型. 本文将基于土与结构相互作用的解析模型研究竖向地震作用下浅埋地下结构中柱的动力响应. 由于单层三跨地铁站为对称结构，为简化计算，取一半进行分析，首先将地下结构看作是刚体，得到刚体在竖向地震分量作用下的动力响应. 之后侧墙对于顶板的约束用抗弯弹簧代替，根据边界条件，将之前的刚体动力响应作为输入，可以求得底板与顶板的弯矩和剪力，从而求得中柱的受力情况.

1单层三跨地下结构运动规律的近似求解

选取的单层三跨地下结构如图1所示. 当顶板在中柱所在截面的剪力已知时，即可得到中柱受力. 求解顶板动力响应时所需的边界条件根据侧墙的运动规律给出. 将地下结构看作刚体，则侧墙的运动规律可以通过刚体与地基的相互作用得到. 地下结构的位移与底板在x=0与x=L处的位移相等.

(1)

由达朗贝尔原理，可以得到结构的运动方程为：

(2)

其中，将结构与覆土看作整体，质量为M:

地下结构的绝对位移：

(3)

2求解地下结构顶板动力响应

利用结构的对称性可以使问题的分析简化，所

以取地下结构一半进行分析说明，设侧墙与底板为刚性的，顶板为弹性的，侧墙刚性联结在底板上. 该地下结构的纵向尺寸远大于其直径及其边长，将顶板沿轴线方向取单位长度，这样可以将顶板简化为梁.

取微元体进行受力分析，根据竖直方向平衡条件和力矩平衡条件，略去二阶微量，可得顶板的自由振动方程与强迫振动方程[9]：

(4)

(5)

由于式(4)为线性的，采用分离变量法来进行求解[10]. 得到两个独立的常微分方程:

(6)

(7)

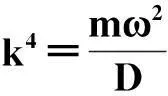
Y(x)=A1coskx+A2sinkx+

A3coshkx+A4sinhkx

(8)

为了分析较为简便，使用抗弯弹簧来代替侧墙对于顶板的抗弯作用，抗弯弹簧系数为kφ，如图3所示.

那么，顶板梁的边界条件为：

x=0时，Y′(0)=0，Y″(0)=0

x=L时，Y(L)=0，DY″(L)=ML=-kφY′(L)

将以上两组边界条件分别带入式(8)，整理可以得到顶板梁的频率方程：

(sinkLcoshkL+coskLsinhkL)+

上式为关于kL的超越方程，通过数值法可以得到kL的值，然后可以得到顶板的振动频率，之后可以求得A1～A4的值，最后便可得到顶板的振型方程. 对于顶板振动第一振动模态，特征值为(kL)1=2.891 2.

3算例

设侧墙墙厚δw=0.7m，顶板内侧板面与底板内侧板面之间的距离hw=5.5m，中柱截面尺寸1.5m×1.5m，侧墙的抗剪系数kτ=0.7×108N/m3，混凝土杨氏模量E=2.35×1010N/m2，泊松比ν=0.16，地基系数kg=2.0×108N/m3，顶板梁长度L=8m，顶板厚δc=0.7m，顶板梁密度ρc=2 400kg/m3，覆土层厚度为4m，密度ρs=1 800kg/m3.

7.244×108Nm

振型为：

Y1(x)=coskx+0.923 8sinkx+

coshkx-0.923 8sinhkx

(9)

其中:

利用振型的正交性来求解顶板的运动方程，得到有阻尼运动方程：

(10)

式中,Mn为广义质量,Pn(t)为广义力. 对于第一振型，可以求得广义质量与广义力分别为M1=16.190m，P1(t)=50.130msin50t，可以得到广义坐标方程为:

当ζ1=0.1时，稳态解的形式为:

φ1=A1sin(50t-φ1)

其中:A1=2.54×10-3m

对于第一振型：

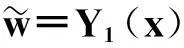
coshkx-0.923 8sinhkx)sin(50t-φ1)

顶板受到的剪力为：

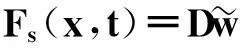
DA1k3(sinkx-0.923 8coskx+

sinhkx-0.923 8coshkx)sin(50t-φ1)N

那么可以得到中柱所在截面处顶板剪力大小为：

2.74×105×sin(50t-φ1)N

当柱间距取3m时，中柱所受到的轴向力大小为:

F=3×Fs(3.15,t)=8.23×105×sin(50t-φ1)N

地下结构顶板与覆土的静重力:

G=2.32×105N

通过以上计算看以看出，在竖向地震作用下，中柱的受力是显著的，约为静重力的3.55倍.

4结论

本文采用结构动力学方法，通过求解地下结构顶板的动力响应得到了单层三跨地下结构中柱在竖向地震分量作用下的受力情况. 地下结构首先被看作是刚体，利用地下结构与地基的相互作用得到地下结构在竖向地震分量作用下的动力响应. 其次，由于地下结构的对称性，取一半进行简化分析. 再次，侧墙对于顶板的约束用抗弯弹簧代替，根据边界条件，将之前的刚体动力响应作为输入，可以求得顶板的剪力. 最后，通过之前求得的顶板的剪力进而求得中柱的受力情况. 通过算例中的计算结果可以看出，竖向地震分量对中柱的作用是显著的，甚至会对地下结构中柱产生破坏，所以竖向地震作用对于地下结构的影响是不能忽视的.

参考文献：

[1]Newmark N M, Blume J A, Kapur K K. Seismic design spectra for nuclear power plants[J]. Journal of Power Division, 1973, 99(2): 287-303

[2]姚小彬，戚承志，陈国兴.一种求解地下结构顶板频率和振型的方法[J].防灾减灾工程学报，2011，31(6)：687-694

[3]于翔，钱七虎，赵跃堂，等.地铁工程结构破坏的竖向地震力影响分析[J].解放军理工大学学报(自然科学版)，2001，2(3)：75-77

[4]李信桥，戚承志，李国华.浅埋地下结构受竖向地震作用的数值模拟[A]∥第二届全国工程安全与防护会议论文集[C]. 2010:832-841

[5]杨春田.日本阪神地震工程的震害分析[J].工程抗震，1996，17(2)：40-42

[6]Qi Chengzhi, Chen Canshou, Davis C A, et al. Simplified analysis model of seismic soil-underground box-type structure interaction[J]. In: Challenges and Advances in Sustainable Transportation Systems, 2014:691-699

[7]王越，戚承志.竖向地震分量对于地铁站动力反应影响的研究[J].山西建筑，2009，35(1)：81-83

[8]戚承志，陈灿寿，钱七虎，等.浅埋地下结构顶板在竖向地震作用下的动力响应[A]∥第二届全国工程安全与防护会议论文集[C]. 2010：691-697

[9]杨桂通.弹性力学[M].北京：高等教育出版社，1998：179-184

[10]刘晶波，杜修力.结构动力学[M].北京：机械工业出版社，2007：160-162

[11]龙驭球.弹性地基梁的计算[M].北京：人民教育出版社，1981：90-94

[责任编辑：佟启巾]

Dynamic Response of Mid-Pillar Under Vertical Seismic Excitation in Treble-Span Shallowly Buried Underground Structure

Yang Jinrui,Qi Chengzhi,Wei Xiaokun, Liu Tiantian

(School of Civil and Traffic Engineering, Beijing Higher Institution Engineering Research Center of Structure and New Materials, Beijing University of Civil Engineering and Architecture, Beijing 100044)

Abstract:Using the structural dynamics method the dynamic response of mid-pillar under vertical seismic excitation in treble-span shallowly buried underground structure is gained by solving dynamic response of underground structure roof slab. Firstly, underground structure is treated as rigid body and the dynamic response of structure under vertical seismic excitation is obtained by analyzing the interaction between rigid body and foundation. Secondly, due to the symmetry of the underground structure, half of the structure is taken into consideration. Bending restraint of side wall which is replaced by bending spring is taken into consideration. Shear forces of roof slab is obtained by inputting the dynamic response of the rigid body obtained previously as boundary condition of roof slab. Finally, the stress of mid-pillar is obtained. The results show that the effect of vertical seismic excitation is significant for mid-pillar, even causes serious damage for the mid-pillar of underground structure.

Key words:vertical seismic excitation; treble-span; mid-pillar; dynamic response

中图分类号：P315.9; TU435

文献标志码：A

作者简介：杨谨瑞(1990—)，男，硕士研究生，研究方向：结构抗震、岩土力学.

基金项目：国家自然科学基金项目(51174012，51174012);北京市属高等学校创新团队建设与教师职业发展计划项目(IDHT20130512);国家重点基础研究发展计划(973)项目(2015CB0578005)

收稿日期：2015-10-03

文章编号：1004-6011(2016)01-0042-04