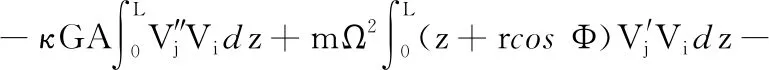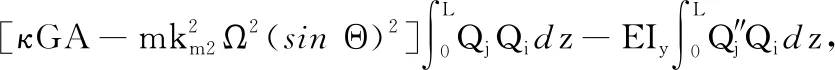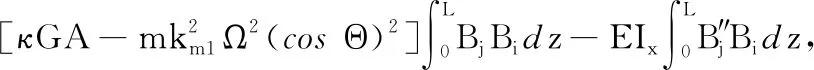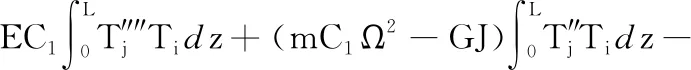旋转径向矩形截面悬臂梁的建模与耦合振动分析

武祥林， 焦映厚， 陈照波

(哈尔滨工业大学 机电工程学院，哈尔滨 150001)

旋转径向悬臂梁被广泛应用于工程实际中，例如航空发动机叶片、直升机旋翼叶片、飞机螺旋桨、风力涡轮机叶片、卫星天线、机械臂、燃气轮机转子叶片等。而对这种悬臂梁的动力学特性的研究，对于指导工程实际具有重要意义，因此，长期以来，很多学者都对旋转径向悬臂梁的动力学特性进行了研究。

早期，许多旋转径向悬臂梁的研究都是基于Timoshenko梁理论，因为Timoshenko梁理论能够考虑剪切变形和转动惯量，具有较高的精度。

Stafford等[1]建立了考虑剪切和旋转惯性的旋转梁解耦滞后和拍击振动的动力学模型，他们使用假定的幂级数解来求解运动方程，并最终求得其固有频率。除幂级数解外，许多研究人员还将有限元方法应用于旋转Timoshenko梁的研究中。Yokoyama[2]应用有限元方法分析了旋转的Timoshenko梁的横向自由振动。Yu等[3]使用有限元方法研究了悬臂式阶梯Timoshenko梁的固有频率和振型。Bazoune等[4]提出了一种模态降阶方法，并将其应用到有限元方法中，用于分析旋转的锥形Timoshenko梁的固有频率和响应。上述研究的建模方法比较简陋，没有考虑由于旋转引了的科里奥利效应，软化效应和应力刚化效应，更无法考虑梁多个自由度之间的耦合。

后来，研究人员在建模过程中开始考虑科里奥利效应，旋转软化效应，应力刚化效应中的一项或两项，但仍然没有全部考虑。

Hashemi等[5]提出了一种动态有限元方法，考虑了科里奥利效应，计算了旋转梁和由该梁构成的旋转结构的固有频率和振型。Oguamanam等[6-9]研究了应力刚化效应对旋转梁固有频率的影响规律。Roy等[10]使用Timoshenko梁模型研究了旋转叶片的自由振动，其中考虑了应力刚化效应和科里奥利效应。Tian等[11]通过使用改进的变分方法和一种多段分割技术建立了旋转梁的动力学模型。考虑了科里奥利效应。研究了科里奥利力和应力刚化效应对旋转梁在不同转速，长细比等情况下的动力学特性的影响。

随着研究的逐渐深入，考虑旋转梁的多个自由度之间的耦合效应成为研究的热点。Hodges等[12]分别使用汉密尔顿原理和经典牛顿力学方法建立了高阶梁的非线性动力学模型。该模型考虑了梁横向弯曲-轴向-扭转变形的耦合，但是该模型非常复杂并且难以求解。Surace等[13]提出了一种积分方法来分析不均匀预扭转梁的展向弯曲振动-弦向弯曲振动-扭转振动。Avramov等[14-15]分别研究了预扭转非对称截面梁和任意截面梁的弯曲-扭转非线性振动问题。 Ozgumus等[16-17]首先研究了锥形Timoshenko梁的展向弯曲振动和扭转振动之间的耦合，然后他们进一步研究了旋转Timoshenko梁的弯曲振动-扭转振动之间的耦合。但上述研究都没有考虑梁轴向伸缩变形的影响。Yutaek等[18]不仅考虑了梁弯曲振动和扭转振动之间的耦合，还考虑了梁弯曲振动，扭转振动和轴向伸缩振动之间的耦合。但是他们的研究没有考虑截面翘曲，且研究结论对于对称截面形状的梁并不适用。

本文提出了一种新的解析方法来建立旋转径向悬臂梁的动力学模型。该模型能够全面考虑科里奥利效应、旋转软化效应、应力刚化效应、梁的剪切变形、转动惯量以及截面翘曲，模型同样考虑了梁的展向弯曲变形、弦向弯曲变形以及轴向伸缩变形和扭转变形之间的耦合效应。为了验证该模型的准确性，将通过采用该模型计算获得的固有频率与3D有限元模型(finite element method，FEM)和文献中的方法所得到的固有频率进行比较。此外，提出了一种改进的表格型模态振型的表示方法，详细研究了不同模态组分之间的耦合，并且深入研究了转速以及安装角对于模态组分的影响规律。

1 建立坐标系

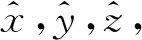
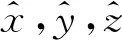
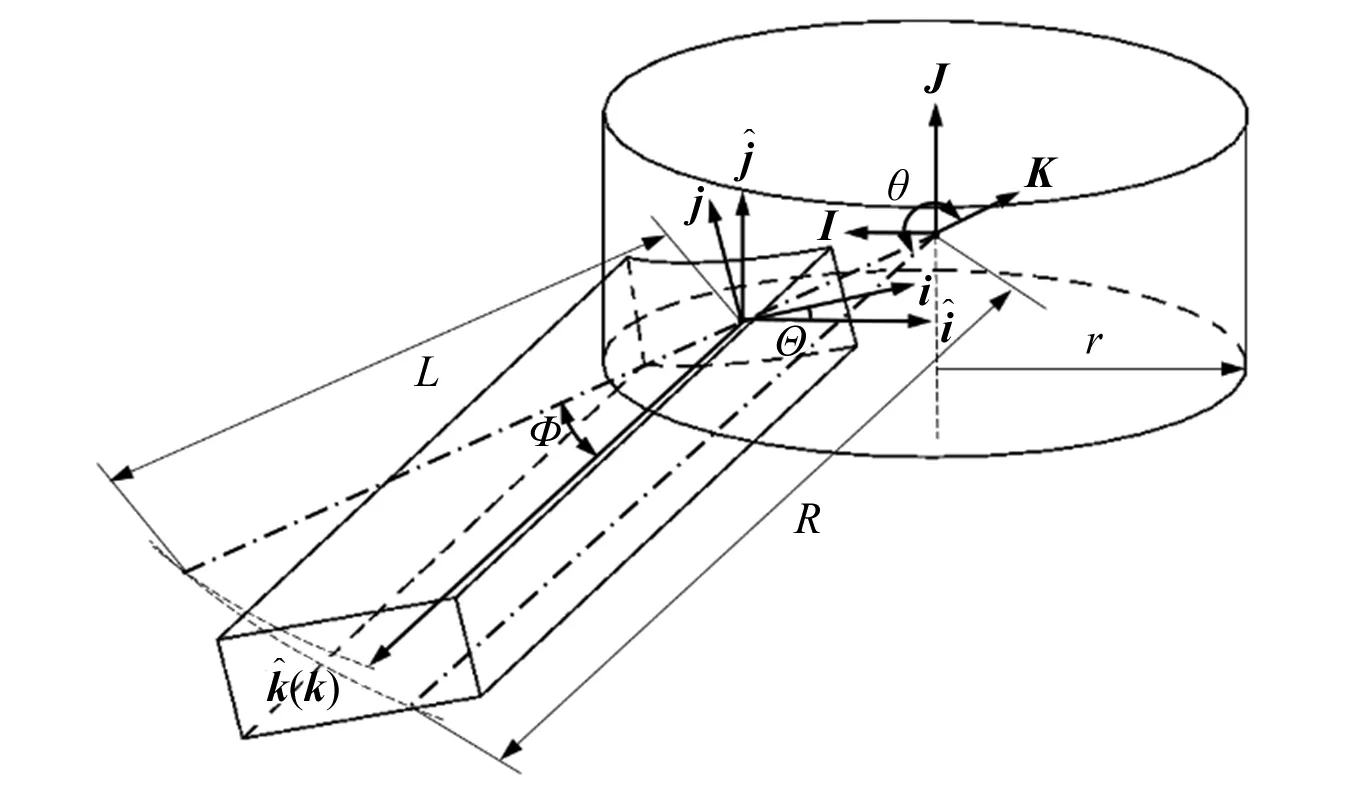
图1 旋转悬臂梁示意图

全局坐标系与固连坐标系的关系可以通过如式(1)表示

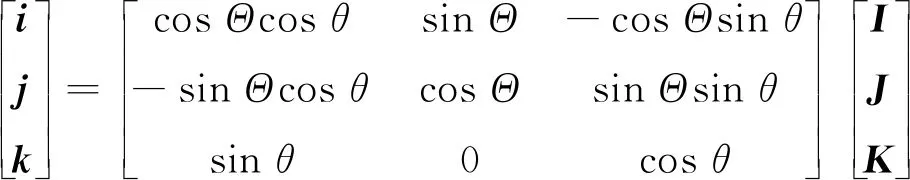
(1)

2 动力学方程建立

创建完坐标系后，就可以建立旋转悬臂梁的动力学方程。为了方便起见，动力学方程建立在固连坐标系x，y，z中，如图2所示。

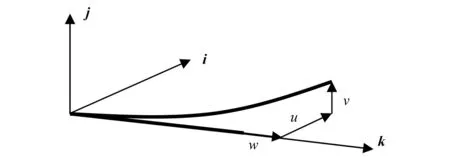
图2 旋转悬臂梁变形示意图

根据弹性理论[19]，可以通过对梁轴线上的点的位移进行泰勒级数展开来获得梁中任意点的位移

(2a)

(2b)

(2c)

其中，

(3)

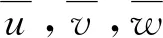
将式(2)代入非线性应变-位移关系中，并经过一系列忽略高阶项的简化处理，可以得到简化后的应变-位移关系为

(4)

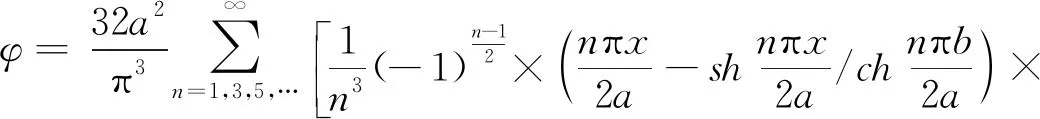
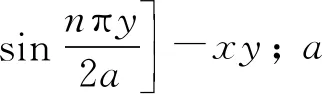
旋转悬臂梁的动力学方程可以通过哈密顿原理得到

(5)

式中：U为梁的弹性势能；T为梁的动能；W为外激励力所做的功，在自由振动分析中，W可以被忽略。

弹性势能可以表示为

(6)

对其进行变分处理，并将式(4)以及梁本构关系代入式(6)中，同时忽略高阶项，最后得到

(7)

式中：E为弹性模量；G为剪切模量；A为横截面面积；Iy和Ix分别为横截面相对x轴和y轴的惯性矩；Ixy=∬Axydxdy为惯性积；J=∬A[(y+φx)2+(x-φy)2]dxdy为考虑截面翘曲情况下的扭转常数，如果不考虑截面翘曲，J等于极惯性矩；C1=∬Aφ2dxdy同样是由于考虑截面翘曲所引入的参数，在以前的参考文献中并不存在。

变形后梁内任意一点的位置坐标(x1,y1,z1)为

x1=u+x-yγ

(8a)

y1=v+xγ+y

(8b)

(8c)

因此，梁内任意一点的绝对速度可以表示为

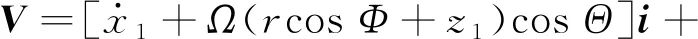
(9)

梁的动能可以表示为

(10)

将式(9)代入式(10)中，并对其进行变分处理，同时忽略高阶项，最后可以得到

(11)

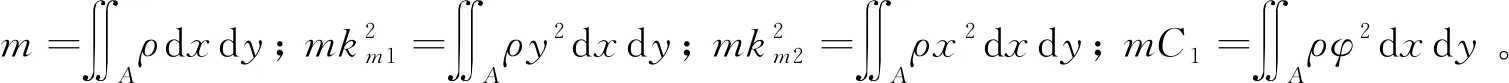
由离心应力贡献的应变能分量的变分同样可以表示为

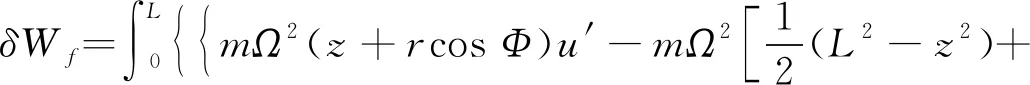
(12)

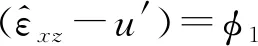
弦向弯曲变形u

(13)

展向弯曲变形

(14)

轴向伸缩变形w

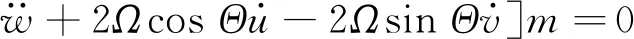
(15)

横截面转角φ1

(16)

横截面转角φ2

(17)

扭转变形γ

(18)

以及边界条件为

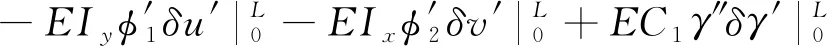
(19)

式(13)～式(18)就是最后建立的横截面形状为矩形的旋转径向悬臂梁的动力学模型。下面我们对上述建立的动力学方程进行求解。

3 动力学方程的求解

应用瑞利-里兹法[21]对所建立的旋转悬臂梁的动力学方程进行求解，首先假设解的形式为

(20)

其中，满足几何边界条件的位移形状函数为[22]

Un(z)=sin(βnz)-sinh(βnz)-
αn[cos(βnz)-cosh(βnz)]

(21a)

Vn(z)=sin(βnz)-sinh(βnz)-
αn[cos(βnz)-cosh(βnz)]

(21b)

Wn(z)=sin(ωnπz),Tn(z)=sin(ωnπz)

(21c)

Qn(z)=sin(ωnπz),Bn(z)=sin(ωnπz)

(21d)

其中，

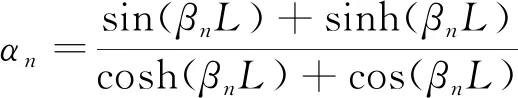
取N阶形状函数的解[23]代入上述动力学方程中去，我们得到矩阵形式的动力学方程

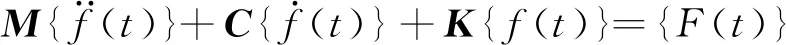
(22)

式中， {f(t)}是由解中的时间项Xn(t)，Yn(t)，Zn(t)，L(t)，R(t)，Pn(t)组成的广义坐标。同时，外激励力向量由离心力组成，质量矩阵M，陀螺矩阵C，刚度矩阵K中的元素如附录所示。这里需要说明的是，上述质量矩阵M除了包括传统上的惯性量，还包括梁横截面翘曲所引起的惯性量，这在以前的参考文献中没有见过。刚度矩阵K中存在由旋转软化效应、应力刚化效应、弦向和展向弯曲变形耦合作用引起的项，而这些项都是转速Ω的函数。除此之外刚度矩阵中还存在由于截面翘曲引起的项。

4 计算结果及分析

表1 叶片(梁)简化模型参数

为了验证当前分析模型的准确性，针对两个不同的无量纲速度，计算了旋转径向悬臂梁的前13阶固有频率，如表2所示。由于位移形状函数的个数“N”对计算结果的精度有很大影响，“N”越大，计算结果精度越高，但是计算效率会下降。因此，为了确保较高的计算精度，同时考虑计算效率，我们取N=8。

表2 当前分析方法与3D有限元方法计算固有频率结果比较(Θ=30°)

表2显示了在同时考虑旋转软化效应和应力刚化效应时，当前分析模型与有限元模型之间的比较。其中：“FB1”是指“一阶展向弯曲固有频率”；“CB1”是指“一阶弦向弯曲固有频率”；“T1”是指“一阶扭转固有频率”；“S1”是指“一阶轴向伸展固有频率”；其他符号与此类似。结果表明，当前分析模型所得的结果与有限元模型的结果吻合较好。

上述分析验证了当前分析模型具有较高的准确性。随后我们又进一步研究了梁弦向弯曲振动与展向弯曲振动的耦合效应对梁固有频率的影响规律。我们将当前分析模型所得的结果与有限元模型的结果以及采用Sinha方法所得到的结果进行比较，如图3所示，其中设置了安装角为30°，无量纲长径比为100。

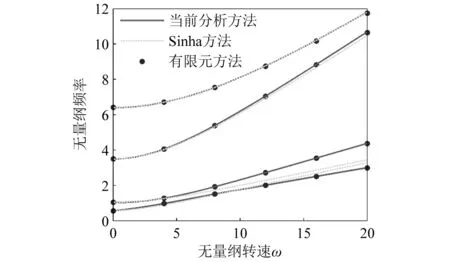
图3 前四阶固有频率随无量纲转速的变化规律

图3表明，采用当前分析模型所得的结果与有限元方法所获得的结果吻合的较好。然而，当无量纲转速超过5时，采用Sinha的方法计算得到的前两阶固有频率与当前分析模型及有限元模型所得到的结果开始出现差异，并且随着转速的增加差异变大。当无量纲转速超过12时，第三阶固有频率开始出现差异。出现这种现象的原因是Sinha的方法没有考虑梁弦向弯曲振动和展向弯曲振动之间的耦合效应。这表明，弦向弯曲振动与展向弯曲振动的耦合效应对旋转悬臂梁的前三阶固有频率有重要影响，如果忽略这种耦合效应，将导致前三阶固有频率的计算不准确。

除了研究固有频率，模态振型的研究也非常有意义，因为模态振型同样包含有动力学系统固有特性的大量信息。但是，在平面图形上绘制三维形式的模态振型非常困难，尤其是当模态振型包含多个模态分量(展向弯曲，弦向弯曲，扭转变形和轴向变形)时，很难从三维模态振型中看出各个模态组分所占的比例。并且如果我们想研究转速对模态振型的影响，我们需要为每一个转速绘制一个含有多个模态组分的模态振型，这很麻烦。为了克服这个困难，我们在Yutaek等研究的基础上，提出了一种改进的表格型表示振型的方法。我们将组成特定模态振型的模态组分分为四类，并使用百分比来定量表示每种模态组分所存储的应变能在当前模态振型所存储的总应变能中所占的比例。该方法很好地解决了上述不便。

图4显示了这种改进的模式振型的表示方法，该图显示了在四个无量纲转速，同时安装角度为30°的时候梁前9阶模态振型的模态组分。图4中的符号S1，S2，FB1-FB4，CB1-CB3，T1分别表示：第一阶轴向伸缩变形模态组分，第二阶轴向伸缩变形模态组分，第一～第四阶展向弯曲模态组分，第一～第三弦向弯曲模态组分以及第一阶扭转模态组分。图中的9行表示了9阶模态振型，每一行所表示的特定模态振型由四种模态组分组成，图中的数字表示模态振型中特定模态组分所占的百分比，为简洁起见，将忽略百分号(%)，同时空网格表示网格中的数字为零。

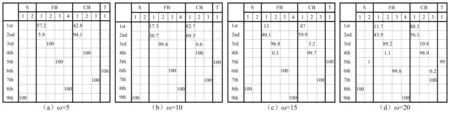
图4 不同无量纲转速下的前9阶模态振型(Θ=30°,δ=100)

从图4中可以看出，转速对于模态振型中的模态组分具有重要影响。随着转速的增加，模态组分之间的转换会发生。例如，随着转速的增加，第一、第三阶模态振型中的展向弯曲模态组分所占比例下降，弦向弯曲模态组分所占比例上升，而第二、第四阶模态振型的情况正好相反。除此之外，随着转速的增加，第五阶模态振型与第六阶模态振型的组分会发生互换，然后随着转速的继续增加，第五阶模态振型中轴向伸缩模态组分所占比例增加，扭转模态组分所占比例减小，第六阶模态振型中展向弯曲模态组分比例减小，弦向弯曲模态组分比例增加。

图4还说明了在较低转速时，只有低阶模态振型由多个模态组分组成，且模态组分会发生转换，而高阶模态振型只有一个模态成分，随着转速的增加，高阶模态振型逐渐从单一模态组分转换为包含多个模态组分，并且模态组分之间开始出现转换。

同时，图5和图6中分别显示了安装角度分别为45°和60°时梁前9阶模态振型的模态组分。对比图4，图5和图6可以看出，无论安装角或者转速如何变化，对于梁特定的模态振型，展向弯曲模态组分与弦向弯曲模态组分之间存在耦合效应，轴向伸缩模态组分和扭转模态组分之间存在耦合。而弯曲模态组分与扭转模态组分之间或弯曲模态组分与轴向伸缩模态组分之间几乎没有耦合。产生这种现象的原因是该梁截面形状对称且材质均匀以及不存在预扭转角。如果考虑梁截面形状不对称或者材料材质不均匀所带来的梁的弯曲中心与形心不重合(偏心率)以及预扭转角，将会发现更多的耦合效应，这些将在以后进行研究。

图4、图5和图6还显示，安装角会对模态振型中模态组分的比例具有重要影响。对于相同的转速，不同安装角下模态振型中模态组分的比例是不同的。

图5 不同无量纲转速下的前9阶模态振型(Θ=45°,δ=100)

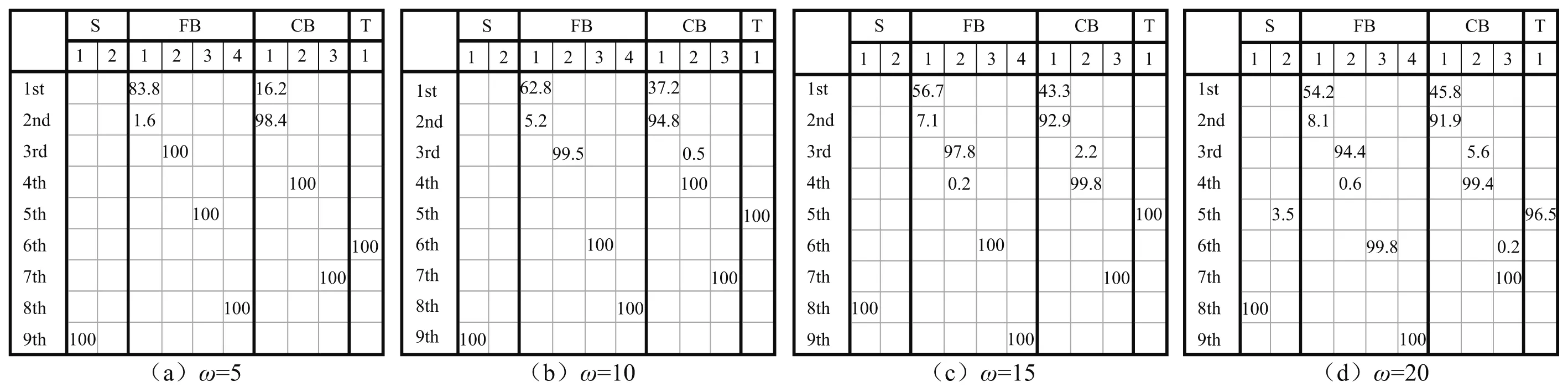
图6 不同无量纲转速下的前9阶模态振型(Θ=60°,δ=100)

为了详细的研究这种不同，我们描述了在不同无量纲转速下，模态振型中的模态组分随安装角的变化规律，如图7所示。图中不同线型的线表示的是不同阶次的模态振型，而组成该模态振型的模态组分在图中都是由文字标出，图中纵坐标表示的就是模态组分所占的百分比。对于只有单一模态组分，并且模态组分不随安装角变化而变化的模态振型，图7中没有给出。

从图7中我们可以看出，当安装角为0°和90°的时候，无论转速为多大，特定的模态振型中只存在一种模态组分，当安装角由0°变化到90°的过程中，模态振型中的模态组分的比例发生变化，并且这种变化受到转速的影响。

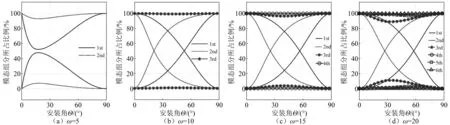
图7 不同无量纲转速下模态组分随安装角的变化规律

在较低速度下，只有低阶模态振型的模态组分会随着安装角的变化而发生变化，例如在无量纲转速为5的时候，只有一阶和二阶模态振型的模态组分会随着安装角的变化而发生了变化，当安装角为0°的时候，一阶模态振型只有一阶展向弯曲变形模态组分，而二阶模态振型只有一阶弦向弯曲变形模态组分，但是当安装角由0°向90°变化的过程中，一阶模态振型中的展向弯曲模态组分所占比例略有下降后又恢复为100%，而弦向弯曲模态组分的比例由0稍有上升后最后又减少为0。同时二阶模态振型的组分由开始的只有一阶弦向模态组分到一阶弦向模态组分的比例大幅度下降，一阶展向模态组分大幅度上升，到最后又恢复为初始状态。

从这里我们可以看出在较低转速下，模态振型中的模态组分随着安装角的增加是没有发生交换的，只是随着安装角增加经过一系列变化后最后又恢复到初始状态。

而在较高转速下，模态振型的模态组分会随着安装角增加而发生转换。例如当无量纲转速为10的时候，第一阶和第二阶模态振型的模态组分就随着安装角的增加而发生了互换。同时我们可以看到，随着无量纲转速由5增加到10，第三阶模态振型开始参与进来，其模态组分开始随着安装角的增加而发生变化，此时由于转速还不够高，所以其模态组分仍然无法转换，只是经过一系列变化后最后恢复为初始状态。

随着转速的继续增加，从图7我们可以看出，逐渐开始有更高阶的模态振型参与进来，同时原来没有发生模态组分转换的模态振型，也开始随着安装角的增加而出现模态组分的转换，而刚刚参与进来的高阶模态振型的模态组分仍然只是随着安装角的增加经历一系列变化最后恢复到初始状态。

5 结 论

本研究采用新方法建立了考虑弯曲变形，轴向变形和扭转变形耦合效应的矩形截面旋转径向悬臂梁的动力学模型。该模型考虑了科里奥利效应，旋转软化效应，应力刚化效应，梁的剪切变形、转动惯量以及截面翘曲。结果表明，该模型具有较高的计算精度，而耦合效应对梁的固有频率和模态振型都有重要影响：

(1) 弦向弯曲振动和展向弯曲振动之间的耦合会影响前三阶弯曲固有频率。在低转速下，如果不考虑耦合效应，计算所得固有频率可以满足精度需求，但时当转速较高时，如果不考虑耦合效应，将导致固有频率的计算结果不准确。

(2) 对于截面形状对称不存在偏心率及预扭转角的旋转悬臂梁，同样存在展向弯曲振动与弦向弯曲振动之间的耦合以及轴向振动与扭转振动之间的耦合，但不存在弯曲振动与扭转振动以及弯曲振动与轴向振动之间的耦合，对于存在偏心率以及预扭转角的旋转悬臂梁的研究，会在后面的研究中继续进行。

(3) 转速对于模态振型中的模态组分具有重要影响。转速的增加会使模态振型中的模态组分发生转换，并且转速较低时，只有低阶模态振型的模态组分会发生转换，随着转速增加，逐渐有较高阶模态振型的模态组分发生转换。

(4) 安装角对模态组分的比例具有重要影响。当安装角为0°和90°的时候，无论转速为多大，特定的模态振型中只存在一种模态组分，当安装角由0°变化到90°的过程中，模态振型中的模态组分的比例发生变化，并且这种变化受到转速的影响。较低转速下，低阶模态振型的模态组分经过一系列变化后会恢复到初始状态，随着转速的增加，低阶模态振型中的模态组分的变化无法恢复到初始状态，最后会发生转换，而高阶模态振型中的模态组分开始发生变化，并且这种变化可以恢复到初始状态。

附录A

质量矩阵M中的元素

陀螺矩阵C中的元素

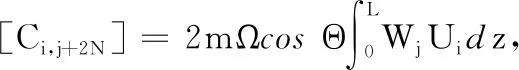
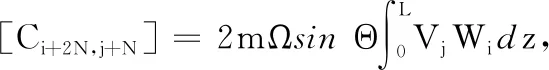
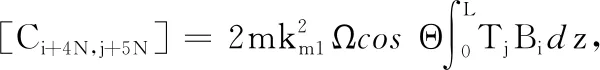
刚度矩阵K中的元素