不确定条件下快递包装回收的逆向物流网络优化研究
2021-07-22韩伟伟罗茵琪
韩伟伟,罗茵琪
(北京邮电大学 现代邮政学院,北京 100876)
一、引 言
网络购物已经成为人们日常工作和生活所需,这一购物方式造成快递产品包装材料的极大消耗,甚至浪费。2020年,全国快递业务量达830亿件,包装废弃物接近1 500万吨,给资源环境带来极大压力[1]。如何快速有效地减少快递运输和快递包装过程中产生的大量垃圾,已经成为整个社会亟待解决的问题。
逆向物流是正向物流的反向流动流,与正向物流相比,逆向物流的结果具有高度不确定性。开展逆向物流研究,关键是要解决各回收点、回收中转站的选址和它们之间的运输线路规划等问题,快递包装逆向物流回收处理网络优化研究已成为一项十分紧迫的任务。
Alshamsi 等[2]建立了一个复杂的逆向物流网络规划系统,包括设施位置的选择、逆向物流中心和再制造设备的容量设计以及运输方法的选择等。Trochu 等[3]分析了回收点的位置和回收中心的容量以及不确定的需求因素,建立了混合线性规划模型,并以最小化成本为目标。Ayvaz 等[4]从第三方回收公司的角度建立逆向物流回收网络,考虑到逆向物流网络设计优化上具有的不确定性因素,提出具有多级、多产品和资源限制的通用两阶段随机规划模型。
国内学者米宁[5]构建了两个模型:一个是基于现有正向物流系统的产品回收网络模型,另一个是通过整合和优化正逆向物流而构建的网络模型。岳辉[6]介绍了涉及第三方的逆向物流网络的建设和具体决策,包括重复使用和再制造两部分。马祖军等[7]分析了再制造物流网络系统,提出一种再制造物流优化模型,该模型可以最小化再制造物流设备的投资和运营成本以及设施之间的运输成本。Kang等[1]1构建了自适应环境影响评估模型,对我国快递业包装废弃物产生量和快件物流运输和配送过程中产生的环境影响(碳排放量)进行估算,并采用情景分析方法和预测模型对快递业减排模式和潜力进行了深入探讨和可行性分析。徐娟等[8]提出企业自营物流回收模式,即自营物流企业通过建立回收点和再制造中心对循环箱进行回收、处理、再利用的逆向物流过程,以回收网络总成本最低为目标函数,建立混合整数规划模型。慕晶晶[9]采用聚类分析法分析各个地区的消费水平和居民购买力,并据此对快递包装回收中转站进行等级划分。程博等[10]针对高校快递包装回收问题建立包含垃圾回收工厂、高校回收站点、各寝楼与菜鸟驿站的三级逆向物流网络模型,所建模型为整数模型,运用重心法进行选址决策。黄周[11]构建了包含客户群、快递回收点、回收中转站以及包装制造厂四级网络节点的逆向物流网络,并利用遗传算法解决选址决策和流量分配问题。
然而,快递包装逆向物流在包装供求、回收数量、回收时间和回收质量方面还有很多不确定性因素,这为逆向物流网络的运行和管理带来了很大的困难。
一是快递包装的供求具有不确定性。在快递包装供应方面,包装来源广泛、数量较大、种类繁杂、原材料使用寿命各不相同,导致很难对回收的快递包装进行快速处理并再次投入使用。在快递包装需求方面,很难准确预测一定时间内快递包裹的数量,而回收的纸箱作为快递纸箱的部分来源,其供应量如果不足将会影响快递包裹的交付。因此,提高对快递包装交付的期望和对快递包装需求量作出准确预测都与所设计回收网络的有效性有关。
二是回收数量具有不确定性。回收数量的不确定性不仅与快递包装交付的不确定性有关,而且与回收率的不确定性有关。影响回收数量的因素主要包括回收价格、回收商之间的竞争、广告投资的回报率和遍及度、消费者对回收包装的便利性要求等,这些因素均可能影响到消费者对快递包装价格的心理期望,进而影响快递包装的回收数目。
三是回收时间具有不确定性。广泛的原材料来源、快递箱的类型、产品生命周期和技术的更新等因素均会对快递回收时间带来影响,进而影响快递运送、库存治理和包装回收成本等。
四是回收质量具有不确定性。通常,不同质量水平的废弃物品具有不同的回收方法和不同的再利用价值,回收质量的不确定性将影响回收产品的收益和再生数量。回收快递包装的目的是获得用于再制造的原材料,因此,在回收快递包装盒时,有必要确定其是否满足原材料再生的要求。
在设计和运行逆向物流网络的过程中,存在诸多不确定性因素,决策者无法提供许多参数的准确值或无法用概率来对其进行描述;因此,有必要在逆向物流过程中使用模糊理论对模糊不确定性进行描述。笔者拟基于快递的回收数量、回收处理时间和丢弃率不明确的情况对快递包装回收网络进行优化设计。
二、模型构建
(一)问题描述
快递包装将由专门的人员收集到回收点,快递行业可以有效利用这些包装资源,而剩余资源将被运到预先安排的回收中转站进行统筹处理,从而实现快递包装资源的有效回收利用,并最大限度地降低回收成本。
假设每一个回收中转站都具有足够的库存能力,并且在产品的每个回收周期都有足够数量的回收车辆从回收中转站出发,然后到达每个负责收集工作的快递包装回收点,每个回收点的位置是恒定且已知的。车辆根据最佳运输路线在快递回收点之间行驶,到达回收点后对回收的快递包装进行简单处理,然后将其运至回收中转站存放,最后根据指定的库存策略对回收的快递包装进行统筹处理。
(二)数量模糊环境下快递包装逆向物流网络设计
1.模型的假设条件
模型的假设条件为:
(1)考虑的是单一产品、单一周期的回收;
(2)回收中转站具备充足的库存容量,拥有足够的运输车辆;
(3)在用度方面,重点考虑运输用度、设施的固定建设用度、单位运营的用度等,而不考量时间成本、社会效益等;
(4)已知回收中转站的最大处理能力、单位运营成本;
(5)已知备选的回收中转站和各回收点的地址信息,并选择此中符合限制条件要求的备选地点进行回收中转站的建设;
(6)将模型中各回收点快递包装的回收量作为模糊变量来处理。
2.模型描述
基于上述假设,给出该问题建模过程中所需要的参数和变量定义,即:
i:回收点标号,i∈I;
j:回收中转站标号,j∈J;
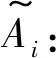
Pj:回收中转站j处理快递包装盒的单位处理成本,j∈J;
Qj:回收中转站j对快递包装盒的最大处理能力;
Fj:建设回收中转站j的固定费用;
dst:任意两点间距离;
m:回收中转站j的丢弃率;
u:快递包装盒的残值;
G:回收车辆的容量;
C:单位距离运费;
k:回收车辆(k=1,2,…,K);
r:客户需求点(r=1,2,…,R);
n:回收点与中转站的集合(n=1,2,…,N)。
决策变量为:
yj:0~1变量,表示备选回收中转站j是否被选中,0表示不被选,1表示被选;
yij:0~1变量,表示中转站j是否为回收点i服务,0表示不为其服务,1表示为其服务;
yik:0~1变量,表示车辆k是否为回收点i服务,0表示不为其服务,1表示为其服务;
ystk:0~1变量,表示车辆k是否经过线路(s,t),0表示不会经过,1表示会经过;
Xij:经回收点i运送到回收中转站j的快递包装盒的数量;
Xjr:经回收中转站j运送到客户需求点r的快递包装盒的数量。
目标函数为
(1)
该模型以总成本最小为目标,总成本包括建设成本、运费和处理成本。每个回收点只能被一个回收中转站服务,每个回收点只能有一辆车经过,任一车辆只能通过一个中转站。回收点流量平衡,回收中转站流量平衡。各回收点到任一回收中转站的总回收量不超过该回收中转站的最大处理能力。在回收路径上,总回收量不超过车辆容量。回收数量为非负以及一些0~1决策变量。
由于约束条件中存在模糊参数,模型中含有模糊参数的式子没有明确的意义,对于这类非线性规划问题,可以根据Liu等[12]提出的模糊机会约束规划方法将其转化成等价的清晰表达式,进而选择传统的求解方法对等价清晰模型进行求解,带模糊参数的模糊机会约束规划模型可写成
西双说,那简单,现在就可以还你。他将手里的借条折一下,再折一下,然后展开,问罗衫,是不是三等分?罗衫莫名其妙地看着他,搞不懂他接下来会有什么名堂。西双嗤地从借条上撕下一绺,弹一下,甩给罗衫,说,三万块钱的三分之一,正好一万,还你。
(2)
其中,Pos{·}表示{·}中事件发生具有的可能性,α和β表示预先给定的置信水平。
根据上述理论,可将带有模糊参数的数学规划模型转化成模糊机会约束规划模型,即
(3)
其他不含模糊参数的约束条件则和原模型中的约束没有差异。此中Pos{·}表示{·}中事件发生的可能性,机会约束则表示约束条件得以满足的可能性应当最少实现预先确定的置信水平α的限制条件。
为了将式(2)转化为相应的等价形式,给出以下定理[13]。
定理1假设模糊向量ξ退化为一个模糊变量ζ,其隶属函数为μ,若函数的形式为g(x,ζ)=h(x)-ζ,则当且仅当h(x)≤Kα,Kα=sup{K|K=μ-1(α)}时,Pos{g(x,ζ)≤0}≥α。
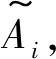
(4)
由此可得以下引理。


根据引理1至引理3,可将约束(3)转化为如下的清晰等价形式:
(5)
(三)时间模糊环境下快递包装逆向物流网络设计
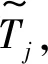
(6)
约束同式(1),目标函数在此基础上增加了处理总时间最小这一目标。
转化为模糊机会约束规划模型,则有
(7)
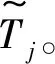
(8)
(四)丢弃率模糊环境下快递包装逆向物流网络设计
基于上述基本假设,快递包装在回收中转站丢弃率模糊的环境下,其规划模型只需把丢弃率设置成模糊变量,即
(9)
其他约束同式(1)。
转化为模糊机会约束规划模型,则有
(10)

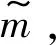
(11)
针对快递包装的回收数量、回收处理时间及回收中转站丢弃率等模糊变量,设计并优化了逆向物流网络。为了实现回收成本最小化,采用模糊规划方法和模糊模拟技术确定模糊机会约束规划模型,并通过模糊仿真技术将其转换为等效的确定形式。
(五)模型求解
本研究数学模型中的决策变量由两个部分组成,只要能够把这些变量确定下来,就能够确定整个快递包装回收逆向物流网络的结构,网络系统中的总成本则可以通过目标函数求得。笔者将模糊规划模型转化为模糊机会约束规划模型,再转化为相应的清晰等价形式,转化后的模型为清晰的混合整数规划模型,可采用传统的求解算法和相应的软件进行求解。
0~1变量yj,yij,yik,ystk组成了决策变量的第一部分,用来表示是否选择建设物流设施或者回收点是否被服务:0表示未被选择或未被服务,1表示被选择或被服务。Xij,Xjk组成了第二部分决策变量,用来表示各物流设施之间的物流量。对第一部分决策变量采用二进制编码方法,取值设置在0和1之间;而对第二部分决策变量会根据各物流设施需求量的不同和物流设施库存容量的不同作相应的改变。在编码的选择上,可以采用混合编码的方式,设置为浮点数编码,取值为实数值。
对定位0~1决策变量的取值依据时间变量随机选取,同时设定取值不能全部为0或全部为1。在一个选址变量固定下来的情况下,对于物流分派量决策变量则采用分段赋值并且加以查验的方式来进行。
步骤1生成的染色体数目为pop-size个,Vk=(Yj,Yij,Yik,Ystk,Xij,Xjk),k=1,2,…,pop-size。
步骤2采取模糊模拟方式分别计算出每一个染色体Vk的目标Zk,k=1,2,…,pop-size。
步骤3定义排序基础上的评价函数。在排序的基础上选择评价函数,对于目前所处该子代中的染色体V1,V2,…,Vpop-size给出一个排序关系,使染色体按照好坏程度重新进行排序。假如参数α∈(0,1)提早给定,则评价函数为eval(Vk)=α(1-α)k-1,k=1,2,…,pop-size。
步骤4经由扭转赌轮来选择染色体的方法实现随机生成新的种群,每扭转一次都会选择出一个染色体。
步骤5交叉操作可以对染色体Vk(k=1,2,…,pop-size)进行更新操作。用参数Pc来表示交叉操作的概率,从k=1到pop-size循环操作以下过程:数r是从[0,1]中随机生成的,若r 步骤6染色体Vk(k=1,2,…,pop-size)经由变异操作来进行种群的更新。采用单点变异,定义变异操作的概率为参数Pm,k从1到pop-size循环进行下述步骤:从[0,1]中随机生成数r,若r 步骤7一直重复步骤2到步骤6,直到给定的循环次数完成为止。 步骤8返回,使目标达到最优的V*k=(Y*j,Y*ij,Y*ik,Y*stk,X*ij,X*jk)染色体,将其作为最优解。 1.数据收集 为某一快递企业构造一个快递包装回收的逆向物流网络,假设已知该快递企业所在区域有26个回收点(如表1所示)和7个备选回收中转站(编号分别为P1,P2,P3,P4,P5,P6和P7),各回收点的回收数量如表2所示。7个备选回收中转站的固定建设成本分别为50万、45万、42万、53万、47万、61万和67万元,单位处理成本分别为0.54,0.57,0.59,0.52,0.56,0.51和0.63元,最大处理能力分别为56.4万、58.2万、53.8万、60万、54.7万、52.6万和57.3万件。 表2 各回收点回收量 各回收中转站的丢弃率均为0.2,不可再用的快递盒单位残值为0.3元。模型中,将回收点的回收量设为梯形模糊数(Ai1,Ai2,Ai3,Ai4)(如表1所示),置信水平α为0.9。模糊模拟1 000次,选择0.6,交叉0.8,变异0.1,种群规模50,单位距离运输费用为5元。 表1 回收点的模糊回收量 2.计算结果 由传统算法得到的计算结果可知,P1,P2,P3,P4,P5和P6为最优解,此时系统的最小总成本为3 042 685.94元,行驶总距离为1 187 49.23米。由混合智能算法得到的计算结果可知,P1,P2,P3,P4和P6为最优解。其中,P4和P5在一条路径上,备选点P7没有被选用,过程和结果如图1至图3所示。此时系统的最小总成本为3 030 951.13元,行驶总距离为114 530.36米。适应度收敛曲线如图4所示。 回收中转站P1的回收线路为P1—1—23—9—10—12—11—P1,行驶距离为27 777.13米。 回收中转站P2的回收线路为P2—18—13—4—2—6—5—P2,行驶距离为20 470.58米。 回收中转站P3的回收线路为P3—22—21—24—25—P3,行驶距离为26 495.98米。 回收中转站P4,P5的回收线路为P4—16—17—14—3—P5—15—19—20—P4,行驶距离为27 644.62米。 回收中转站P6的回收线路为P6—8—26—7—P6,行驶距离为12 142.05米。 4 0003 5003 0002 5002 0001 5001 0005002 0002 5003 0003 5004 0004 5002524P3222112391015P1P2P7P6P51432P412116518134201916177268>DDE(D>D/E(D/;DDC/;+/;?5图1 模糊模拟随机解4 0003 5003 0002 5002 0001 5001 0005002 0002 5003 0003 5004 0004 500P72221242523111121092019161714315P5P3P4P1P2P6181342657268>DDE(D>D/E(D/;DDC/;+/;?5图2 选址过程4 0003 5003 0002 5002 0001 5001 0005002 0002 5003 0003 5004 0004 5002221P324251239P11112105641318P27P68262019P41617141532P5>DDE(D>D/E(DP7/;DDC/;+/;?5图3 路径10.09.59.08.58.07.57.06.56.00102030405060708090100+**;EA;A,D82;A,D;A,×105图4 适应度收敛曲线 分析不同的置信水平α对结果带来的影响可知,在其他参数不变的情况下,随着α的增大,总成本也随之越大。对比两种算法的结果可知,相比传统算法,混合智能算法所得系统总成本和行驶总距离都更小,在企业节约成本方面有着重要意义。 1.数据收集 在前节数据的基础之上,将备选回收中转站的回收处理时间设为梯形模糊数(Tj1,Tj2,Tj3,Tj4),如表3所示,置信水平β=0.9。 表3 回收中转站对快递包装的模糊处理时间 2.计算结果 用混合智能算法计算获得的结果如图5所示,最小成本为3 030 741.86元。从中可以看出,在各回收中转站对快递包装的单位处理时间相差不大的条件下,回收处理时间对模型的稳定性影响并不大。相较于采用传统算法得到的计算结果,选址和回收路线均保持不变,只是各回收点的回收数量略有差异,可知模型对参数有较高的稳定性。 图5 回收处理时间模糊环境下的最优路径 在前节算例数据的基础之上,采用梯形模糊数(m1,m2,m3,m4)来表示回收中转站的模糊环境丢弃率,此处设置为(0.3,0.4,0.5,0.6),用混合智能算法计算得到的结果如图6所示,最小成本为3 030 729.45元。可以看出,小范畴的丢弃率波动情况对模型的稳定性造成的影响不大。结果显示,各回收点的快递包装回收数量没有变动,只是回收路线略有差异,系统鲁棒性较强。 图6 丢弃率模糊环境下的最优路径 分别采用传统算法和混合智能算法对实例进行求解。传统算法是将模糊机会约束规划等价地转化为相应的确定性模型,然后利用MATLAB软件求解以取得最优的全局解;混合智能算法是融合了模拟仿真和遗传算法的方法来获得最优解。 比较传统算法和混合智能算法的计算结果,分析不同的置信度所带来的影响,结果表明:混合智能算法的最优定位结果与传统优化算法所得结果相同,但混合智能算法获得的回收点之间的物流量分布更为实用,而传统算法只能够得到唯一的定位结果。 在参数不确定的情况下,当模糊参数繁杂且难以转化为清晰的等效模型时,选择混合智能算法是一种十分有效的方法。但对于模糊环境下快递包装回收逆向物流网络问题,有时难以确切给出不确定因素的模糊隶属函数,且模糊数中包含着一定的主观因素。模糊集理论弥补了这一缺陷,模糊数的设置更为客观。因此,现阶段进行模糊环境下再利用逆向物流网络设计问题的研究非常必要。同时,在电子商务环境下,企业可回收废旧包装的区域不限于已划分的消费区域,有一些不确定回收源的存在,其位置和快递包装回收数量不能事先确定,应重视此类问题的研究。 基于有关逆向物流网络设计的现有研究成果,笔者深入分析了不确定条件下逆向物流回收网络优化的主要问题,并对所构建的数学模型进行适当的求解算法的研究和设计,主要工作如下:建立基于模糊理论的快递包装逆向物流回收网格,将各个回收点的回收量、回收处理时间和回收中转站的丢弃率等不确定因素作为模糊参数,建立模糊机会约束的数学规划模型,并采纳一种混合智能算法对该模型进行求解。通过数据仿真验证了模型和算法的实用性,并指出不同置信度对网络优化结果的影响。 为实现快递包装材料的再次利用,建立完善的逆向物流回收网络并对其进行优化处理,是减少资源浪费、减轻环境压力、建立友好型社会的重要途径,有助于创造绿色生活。 对快递公司而言,回收快递包装是企业节省成本的有效方法,也是企业应当承担的社会责任。在提倡绿色物流成长之时,实现快递包装的回收再利用是快递企业健康持久发展的必由之路。快递包装回收问题是一个新的社会热点,现有研究成果评价目标比较单一,大多以成本最小化为目的,在不确定情况下缺少对多目标逆向物流体系网络的优化研究。因此,对不确定性条件下快递包裹回收的逆向物流网络的优化问题开展研究意义重大。三、算例分析
(一)数量模糊环境下的算例分析

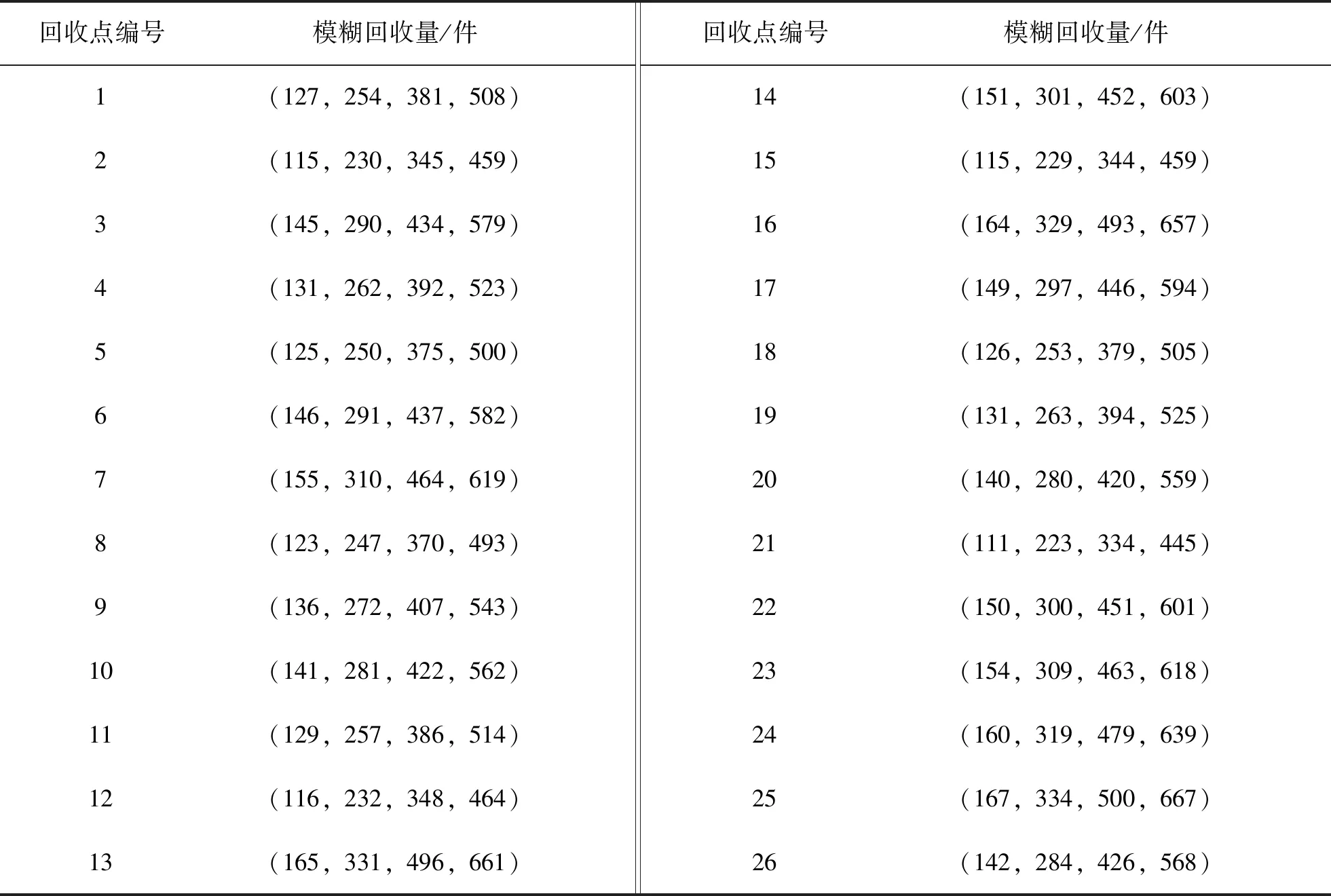
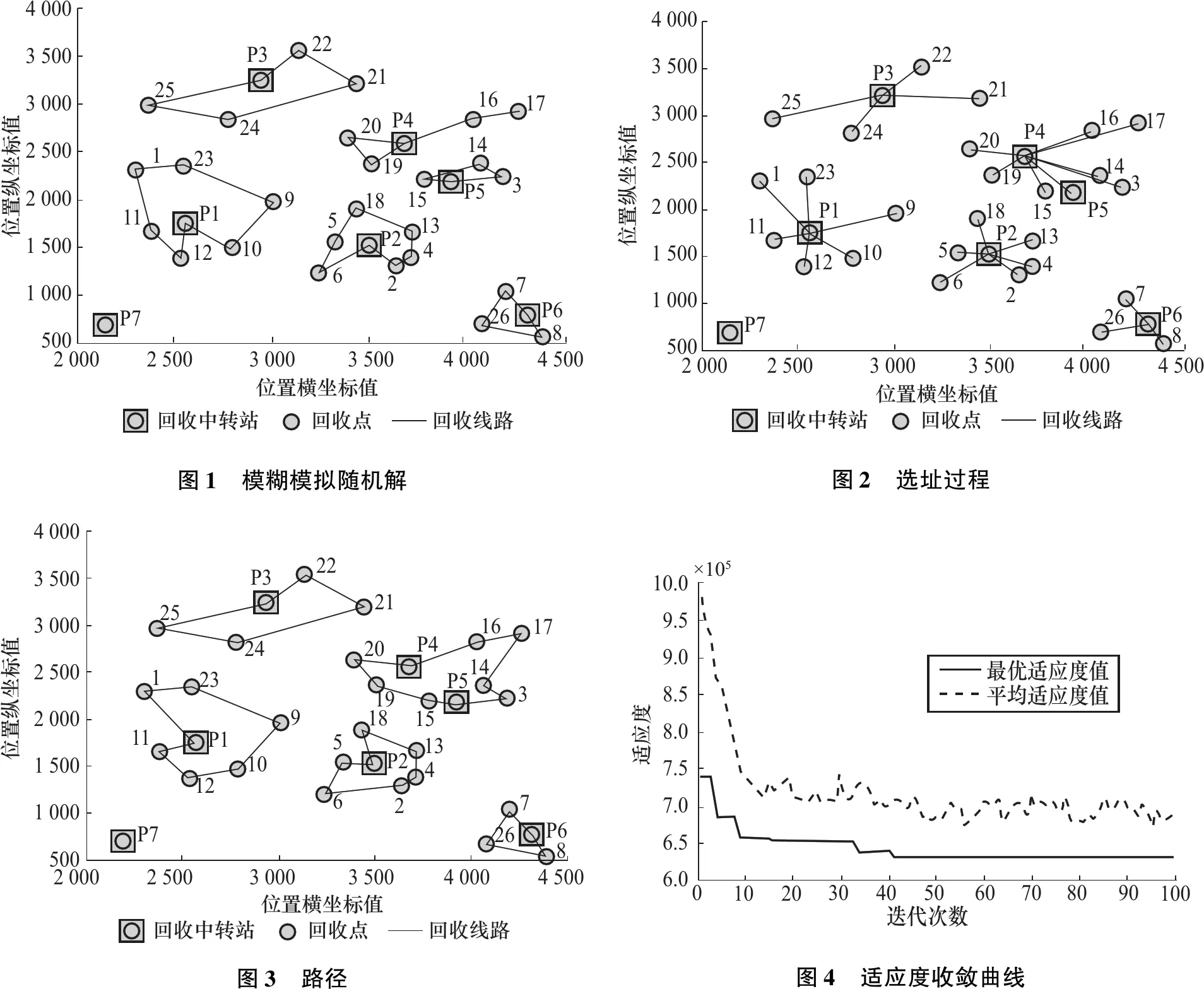
(二)时间模糊环境下的算例分析

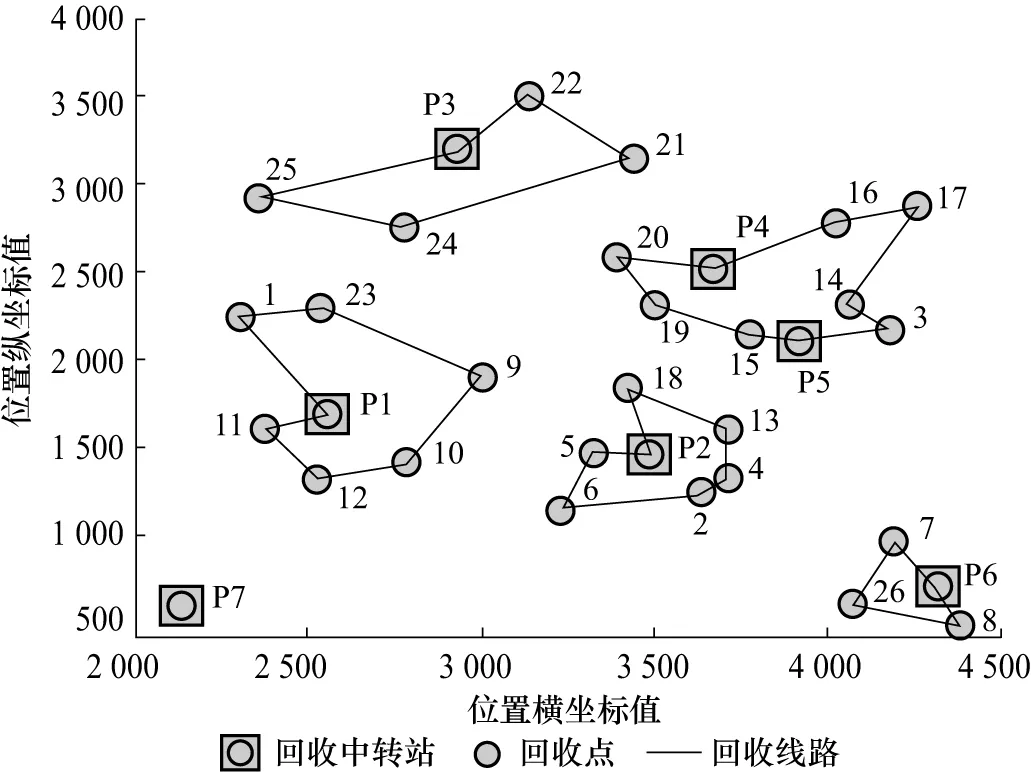
(三)丢弃率模糊环境下的算例分析

四、结 论
