原竹材料抗弯性能试验研究

刘鹏程，周期石，田杰夫，张 海，李 威，付飞扬

(中南大学 土木工程学院，湖南 长沙 410075)

0 引 言

建筑作为中国城市化进程中的重要表现形式，粗放式的建筑发展方式消耗了大量的能源并且产生了大量污染，对生态环境和人类的生命健康造成了严重损害。传统的混凝土结构和钢结构在全寿命周期会产生大量的碳排放，木结构由于木材资源的枯竭在应用上也受到了限制。基于以上问题，科研和工程人员对竹结构的研究兴趣逐步提高。中国是世界竹资源的分布中心，拥有39属500余种竹材，储存量和产量都极其丰富。竹材是一种速生的可再生植物，3～5年即可成材，成材时间远短于木材。竹材具有优异的力学性能，其抗拉强度约为木材的2倍，抗压强度约为木材的1.5倍，强重比优于钢材[1-5]。竹结构单位面积的能耗仅为混凝土结构的1/8及木结构的1/3，竹结构的能耗仅为钢结构的1/50[6]。同时，竹结构也具有优异的抗震性能[7-9]。由此可见，竹材是一种具有替代传统建筑材料潜质的新型建筑材料。

抗弯是竹材重要的力学性能，对于竹材抗弯目前国内外已有相关研究。文献[10]探究了原竹抗弯强度与物理性能的关系，并实现了通过物理性能对竹材进行抗弯强度无损检测。Nurmadina等[11]通过分析不同参数对竹材抗弯性能的影响探究了适合竹材分级的方法。李光荣等[12]研究了竹龄和高度对毛竹抗弯性能的影响。于金光等[13]研究了含水率、竹节和取材单元对毛竹抗弯强度的影响。张丹等[14]开展毛竹圆竹和竹片抗弯对比试验，分析了不同试件形态在试验结果上的差异。上官薇薇[15]分析了含水率和密度对重组竹力学性能的影响，并拟合了重组竹抗弯强度与抗弯弹性模量的关系。然而，尽管目前国内外对竹材性能的研究覆盖了诸多方面，但是都不够系统和深入，并且目前竹结构应用受限的主要原因是缺乏强度设计值的研究。

本文针对毛竹材料开展了竹片抗弯性能试验研究，观察了试件的破坏过程及现象；考虑样本数量的影响分析了原竹材料抗弯强度标准值；基于可靠度理论分析了原竹材料抗弯可靠度指标与抗力分项系数和荷载比的关系，并计算得到了原竹材料抗弯强度设计值。

1 材料与试验

1.1 竹材选取与试件制备

参考《建筑用竹材物理力学性能试验方法》[16]开展原竹材料抗弯试验。试验中采用的原竹材料品种为毛竹，采自湖南省郴州市，取材时间为冬季，竹龄为3～4年，材料径级为100 mm左右，砍伐成长度为6 m的试样运输回实验室，经过锯截、干燥、打磨等流程，加工成尺寸规格为220 mm×15 mm×t(t为试件厚度)的抗弯试件(图1)。

1.2 抗弯强度试验

采用万能试验机对试件进行加载，正式加载阶段加载速率为0.01 mm·s-1，图2为竹片抗弯试验加载现场。式(1)，(2)分别为竹材抗弯强度和弹性模量计算公式。

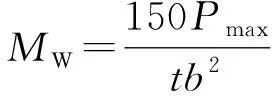
(1)

(2)

式中：MW为含水率W下的抗弯强度；ME为含水率W下的抗弯弹性模量；b为试件高度；ΔP为上下限荷载之差；δm为ΔP作用下试件纯弯段挠度值。

1.3 强度调整

试验结束后，立即从破坏部位截取用于测定含水率的试样，参照JG/T 199—2007[16]，测试竹材的含水率。由于含水率对竹材力学性能具有显著影响，因此需对竹材力学性能进行调整，竹材含水率基准点为12%，本文所有力学性能结果均为12%含水率下的值。式(3)为竹材含水率计算公式，式(4)为竹材强度调整公式。

(3)

(4)

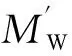
2 竹秆不同部位抗弯性能

2.1 破坏过程及形态

为分析竹秆不同部位的抗弯性能，分别在竹秆3个不同高度h处取材进行竹片抗弯试验，试件信息如表1所示，从下至上3个不同部位的试件依次为B-1，B-2和B-3。不同部位试件抗弯破坏过程和形态均相似，随着加载的进行，竹片弯曲变形逐渐增大，在荷载增大到一定值时试件在加载点处出现明显变形并于底部率先发生开裂。加载至极限荷载时，试件形成上下贯通的裂缝，试件纤维几乎都被拉断(图3)。图4为不同部位试件中心位置处的荷载-位移曲线。由图4可知，竹片在抗弯加载过程中首先经历较长的弹性阶段，塑性阶段较短。随着部位的增高，试件抗弯承载力逐渐降低。

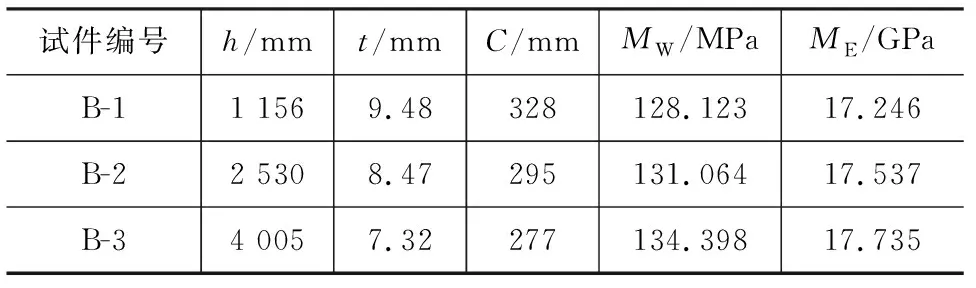
表1 不同部位试件信息及试验分析结果Tab.1 Specimen Information of Different Positions and Test Analysis Results

2.2 力学性能与参数关系拟合

将试件抗弯强度和弹性模量分别与高度、壁厚、周长进行拟合，结果见图5～10。由拟合曲线可知，竹片抗弯强度和弹性模量随着高度的增大和壁厚、周长的减小呈增大趋势。采用线性函数对竹片力学性能与物理参数进行拟合具有较好的效果，拟合公式可对竹材力学性能进行预测。

3 强度标准值的确定

3.1 样本数量对特征值的影响

参考《圆竹结构建筑技术规程》(CECS 434:2016)[17]进行选材，共挑选了116根竹管进行研究，以竹管两端清材小试件强度代表整根竹管的强度，剔除1个强度异常值后的竹管抗弯强度试验结果如表2所示。强度标准值对于竹结构的设计具有重要 意义，目前文献中对于材料强度标准值的计算均为采用一定数量的强度数据直接进行统计分析，然而统计结果随样本数量和试验条件而波动。为分析样本数量对竹材抗弯强度误差的影响，在115个总体样本中随机分别抽取10，30，50，70，100个数据，重复抽样100次，将不同百分位上的数值与对应总体样本中的数值进行对比得到误差值，误差值的统计结果如表3所示，不同样本数量的各分位值误差均值与样本数量的关系曲线如图11所示。由图11可知，随着样本数量的增加，不同分位值的误差均值逐渐减小。对于竹材强度标准值而言，样本数量是不可忽视的因素。

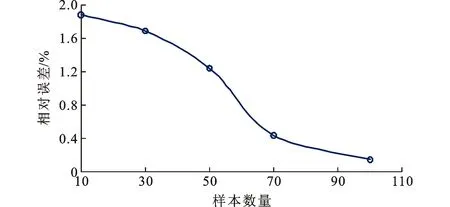
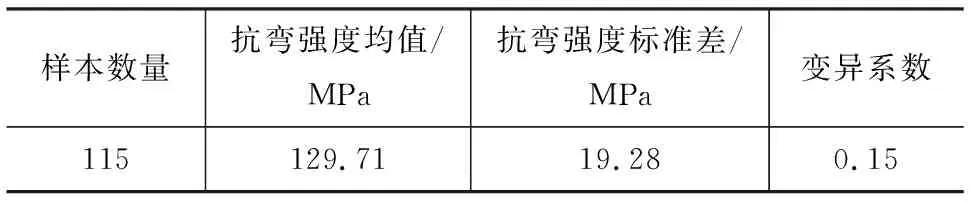
表2 剔除异常值后竹管抗弯强度统计Tab.2 Statistics of Bending Strength of Bamboo Pipes After Removing Abnormal Values

表3 不同样本数量下的分位值误差Tab.3 Quantile Error Under Different Sample Numbers

3.2 竹材抗弯强度标准值

为使竹材抗弯强度标准值具有参考性，本文采用Bootstrap法对抗弯强度进行统计分析。Bootstrap法的思路是从样本容量为a的强度数据X={x1，x2，…，xa}中随机有放回地抽取a个强度值组成一个Bootstrap样本Yj={y1j，y2j，…，yaj}，通过公式(1)，(2)计算样本的均值E和方差S2。循环n次得到样本集B={Y1，Y2，…，Yn}，对n个Bootstrap样本进行统计分析得到的均值和方差用于评价总体参数，其能够较大程度地减小样本数量的影响。式(5)，(6)为通过Bootstrap法进行特征值计算的公式。

(5)

(6)

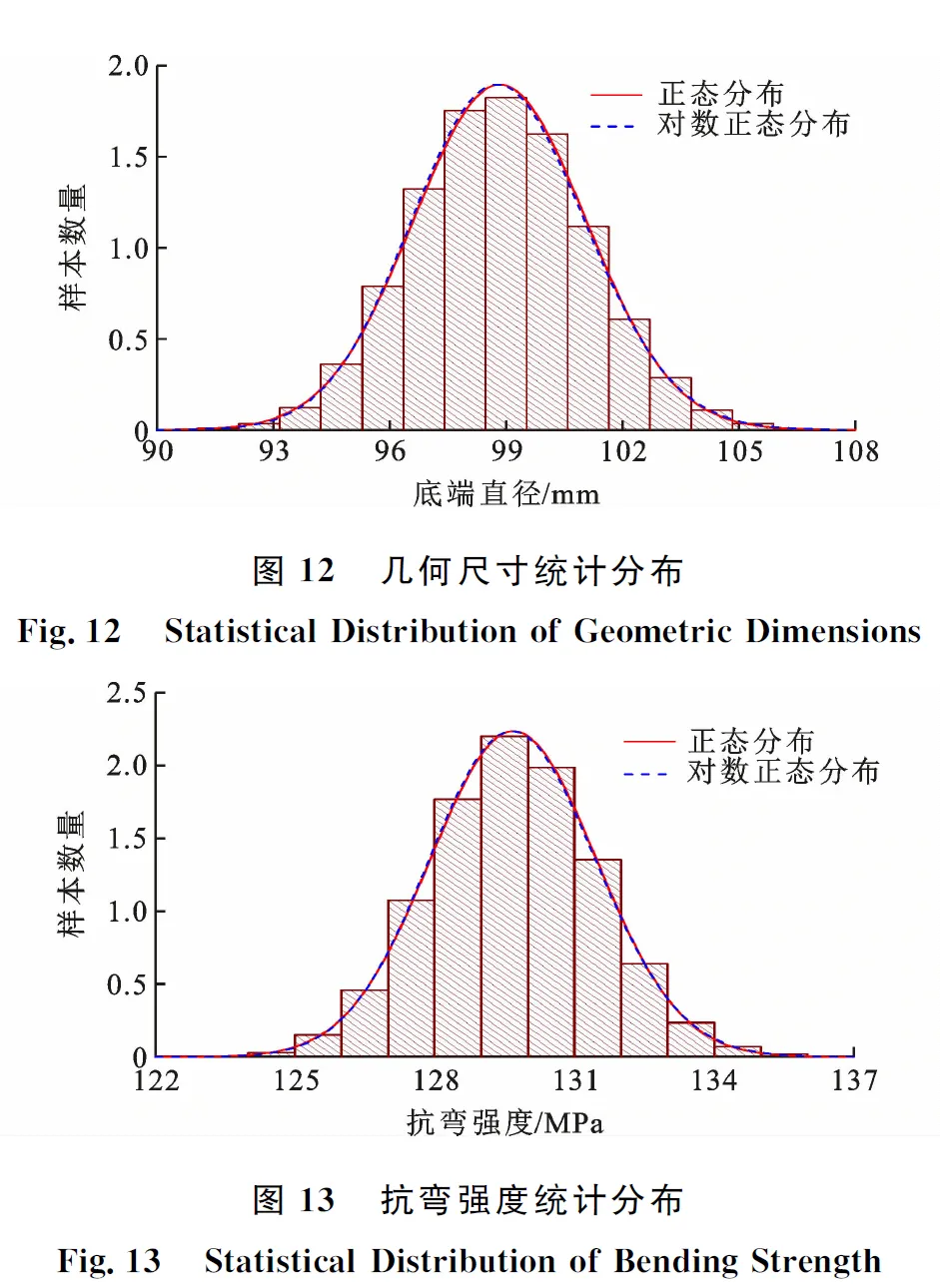
通过Bootstrap法进行10 000次重抽样得到的竹材几何尺寸(底端直径)和抗弯强度结果如表4和图12，13所示。由于采用正态分布和对数正态分布对几何尺寸和抗弯强度值进行拟合的结果极为接近，故本文采用如式(7)所示的正态分布计算式计算标准值。计算得到的几何尺寸标准值为97.28 mm，抗弯强度标准值为126.75 MPa。

fk=μ-kS

(7)

表4 Bootstrap法重抽样10 000次几何尺寸和抗弯强度统计结果Tab.4 Geometric Dimension and Bending Strength Statistical Results of 10 000 Re-sampling with Bootstrap Method

式中：fk为抗弯强度标准值；μ，S分别为抗弯强度平均值和标准差；k为特征系数，取1.645[18]。

4 竹材抗弯强度设计值

4.1 功能函数与统计参数

原竹构件功能函数可表示为[19]

(8)

KQ=KQ1KQ2KQ3KQ4

(9)

式中：G为功能函数；KP为计算模式不定性系数；KA为几何参数不定性系数；KQ为由小试件抗弯强度转换为构件抗弯强度的折减系数；fs为竹材抗弯强度；fk为竹材抗弯强度标准值；KD为长期荷载效应系数；d为恒载与其标准值的比值；q为活荷载与其标准值的比值；ρ为荷载比；KB为作用效应不定性系数；γR为抗力分项系数；γG，γQ分别为恒载和活荷载分项系数；Ψ为荷载效应组合系数；KQ1为考虑天然缺陷影响的系数；KQ2为考虑干燥缺陷影响的系数；KQ3为长期荷载影响系数；KQ4为考虑尺寸影响的系数。

抗力统计参数和荷载统计参数详见《木结构设计规范》(GB 50005—2017)[20]。通过Bootstrap法分析得到的几何参数不定性系数KA(几何参数均值与标准值的比值)为1.01，变异系数VKA为0.01。由于原竹和原木在成分上具有相似性，因此其他抗力统计参数在原木基础上可不考虑调整[21-23]。

4.2 可靠度指标

不同安全等级下结构的可靠度指标如表5所示。由于竹材抗弯的塑性阶段较短，若按照延性破坏考虑则偏不安全，因此本文竹材抗弯目标可靠度按脆性考虑，即在3个安全等级下的目标可靠度指标β分别为4.2，3.7，3.2。

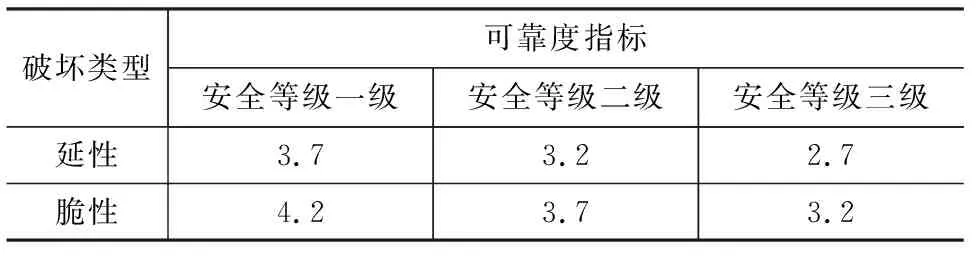
表5 结构构件极限状态下的可靠度指标Tab.5 Reliability Index of Structural Components in Limit State

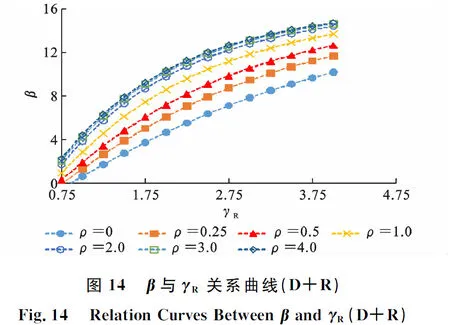
考虑4种荷载组合，分别为恒载+住宅楼面活荷载(D+R)、恒载+办公楼面活荷载(D+O)、恒载+风荷载(D+W)和恒载+雪荷载(D+S)。考虑7种荷载比ρ，分别为0，0.25，0.5，1.0，2.0，3.0，4.0。基于JC法，通过MATLAB程序进行可靠度分析，得到如图14～21所示的结果。由图14～21可知：可靠度指标β随着抗力分项系数γR增大而增大；随着荷载比ρ的增大，可靠度指标β的增幅逐渐减小；可靠度指标β随着荷载比ρ的增大而增大。

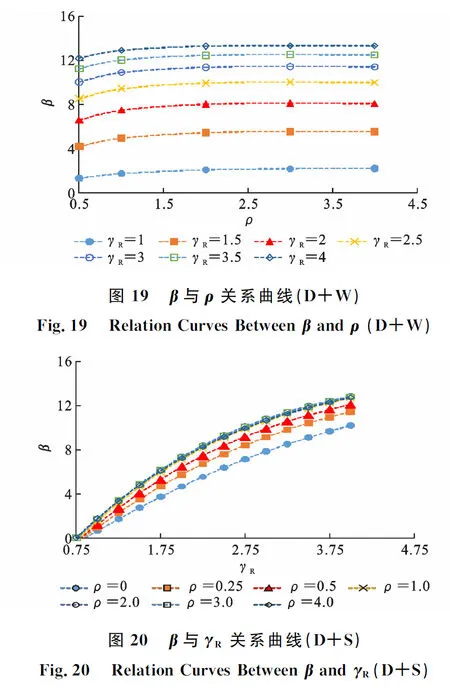
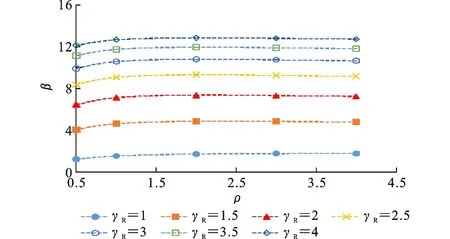
4.3 抗力分项系数

不同目标可靠度指标下竹材抗弯抗力分项系数如表6所示。由表6可知，不同荷载组合和荷载比下抗力分项系数不尽相同。荷载比ρ>0情况下，相 同荷载比时荷载组合D+S下抗力分项系数最大，荷载组合D+O下抗力分项系数最小。

4.4 抗弯强度设计值的确定

竹材抗弯强度设计值fd的计算公式为

(10)

取4种荷载组合下的最大抗力分项系数计算抗弯强度设计值，即3个安全等级下抗力分项系数分别取1.89，1.75和1.63，由公式(10)计算所得原竹材料抗弯强度设计值见表7，3个安全等级下的原竹 材料抗弯强度设计值分别为27.670，29.884，32.084 MPa。

表7 原竹材料强度设计值Tab.7 Strength Design Value of Original Bamboo Material

5 结 语

(1)竹片抗弯加载过程中，竹片下侧纤维首先被拉断，最终形成自下而上的贯通裂缝。试件先经历较长的弹性阶段，塑性阶段较短，竹片抗弯承载力随高度增加而减小。

(2)竹片抗弯强度和弹性模量随高度增加而增大，随壁厚和周长增大而减小，不同部位竹片抗弯强度和弹性模量与高度、壁厚和周长具有较好的拟合优度，拟合公式可对竹材力学性能进行预测。

(3)样本数量对原竹材料抗弯强度抽样结果具有显著影响，本文提出采用Bootstrap法对竹片抗弯强度数据进行统计分析，进行10 000次重抽样并基于正态分布计算得到的竹材抗弯强度标准值为126.75 MPa。

(4)基于可靠度理论得到了可靠度指标β与抗力分项系数γR、荷载比ρ的关系，结果表明，随着抗力分项系数γR和荷载比ρ的增大，可靠度指标β呈增大趋势，但增幅逐渐减小。荷载比ρ>0时，目标可靠度指标下恒载+雪荷载(D+S)的抗力分项系数γR最大，恒载+办公楼面活荷载(D+O)的抗力分项系数γR最小。取各荷载组合下的最大抗力分项系数计算得到3个安全等级下的原竹材料抗弯强度设计值分别为27.670，29.884，32.084 MPa。