圆端形钢管混凝土偏压柱截面优化研究
2021-07-21任志刚徐圣海李培鹏
任志刚,徐圣海,李培鹏,刘 闯
(武汉理工大学 土木工程与建筑学院,湖北 武汉 430070)
0 引 言
钢管混凝土(Concrete-filled Steel Tube,CFST)构件具有承载力高、延性好、制作方便、装配性强、施工周期短等优点,被广泛用于桥梁及装配式结构中。圆端形钢管混凝土(Round-ended Rectangular Concrete-filled Steel Tube,RRCFST)构件结合了矩形钢管混凝土构件抗弯承载能力强与圆形钢管混凝土构件轴压承载力大、延性好的特点[1],逐渐被应用于大型桥梁工程中,如武汉后湖大桥塔柱、厦门杏林湾路段边墩等,图1为武汉后湖大桥塔柱,其中,H,B,t分别为截面高度、宽度和外钢管壁厚度。
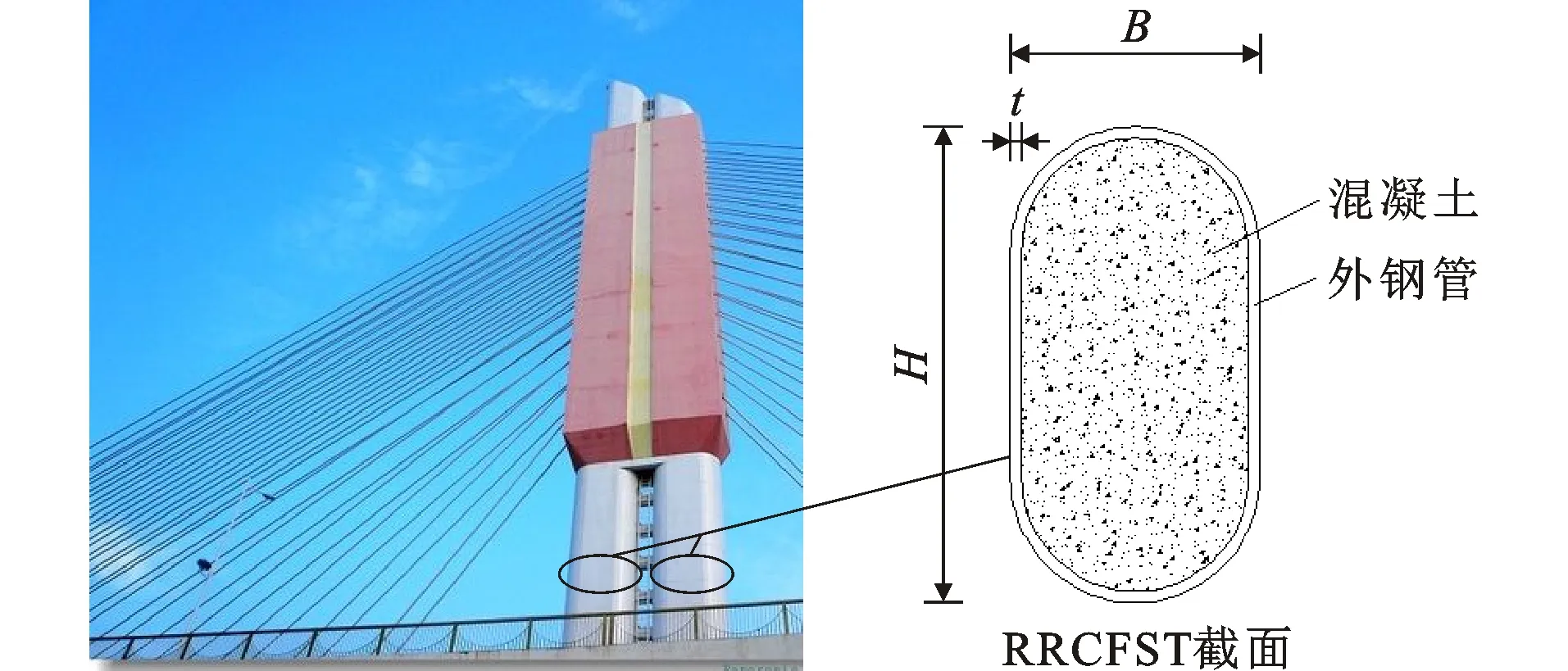
对于圆形或矩形钢管混凝土短柱构件,其轴压极限承载力与构件截面高宽比H/B无关[2-4],对于RRCFST短柱构件而言,因其外管壁对核心混凝土提供的侧向约束效应介于圆形和矩形钢管之间[5-6],特殊的截面形式使得构件截面高宽比H/B与其轴压极限承载力密切相关[7-10]。在承载阶段,RRCFST短柱钢管对核心混凝土提供的约束效应主要集中在圆弧段,随着截面高宽比H/B的变化,钢管对核心混凝土的约束效应也发生变化[1,11-12]。由此则产生了以材料充分利用为目标的RRCFST偏压柱截面优化问题:在所使用的材料强度及用量给定的情况下,随着RRCFST柱截面高宽比H/B的增加,构件轴压承载力减小,同时构件绕强轴的抗弯承载力显著提高[13]。因此产生了基于钢材及混凝土合理、充分利用的RRCFST构件截面高宽比H/B选取问题。
在现有相关RRCFST构件的研究中,少有研究与RRCFST构件截面优化相关。本文通过Python语言利用有限元软件ABAQUS建立了一定数量的RRCFST偏压柱模型,细致研究了圆端形截面高宽比H/B对构件极限受荷能力的影响,并提出了基于材料强度及用量层面的构件承载力快速验算、截面快速确定方法。
1 数据来源及试验简介
1.1 数据来源
本文引用文献[7]中圆端形钢管混凝土短柱轴压试验数据作有限元模型验证,具体构件参数见表1,其中L为构件长度,fcu为混凝土立方体抗压强度,fy为钢材屈服强度,e为加载线与截面强轴的距离,Nu,e为试验测得构件极限承载力,Nu,0为有限元方法分析得到的构件极限承载力,所引用10个构件截面高宽比H/B=2~4。
1.2 试验简介
除引用上述RRCFST构件轴压试验数据外,笔者所在课题组也进行了相应的圆端形钢管混凝土柱偏压试验。混凝土强度由同条件成型养护的立方体试块测得,其强度为30.0 MPa。钢材采用Q235钢材,对4个标准钢材试件进行拉伸试验,测得其屈服强度为254 MPa,极限抗拉强度为318 MPa,弹性模量Es为2.06 GPa,详细内容见文献[14]。
RRCFST-1,RRCFST-2,RRCFST-3为圆端形钢管混凝土构件,其截面高宽比H/B=1.5~2.5,具体构件参数见表1。

表1 构件参数与极限承载力Tab.1 Parameters and Ultimate Bearing Capacity of Specimens
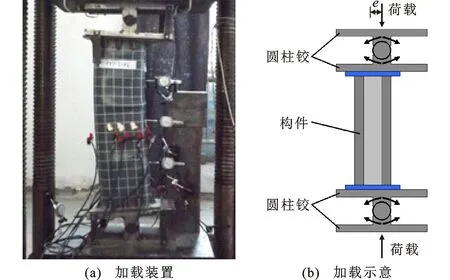
偏压试验在湖北工业大学结构大厅500 t压力机上进行,构件两端固定方式为铰接,实际采用2个 圆柱铰替代,如图2所示。试验采用分级加载方式进行加载,按估算最大荷载的10%逐级增加,当荷载即将达到估算最大荷载时,缓慢减小荷载增速至估算最大荷载的5%;每级荷载的持荷时间为2~3 min,接近破坏时慢速连续加载直至构件破坏。
2 有限元模型建立与验证
2.1 概 述
本文采用非线性有限元分析软件ABAQUS进行模型建立及分析计算。考虑到模型及所加荷载的对称性,所有模型均采用1/2模型进行建模分析。模拟采用加载线方式施加位移荷载,荷载通过大刚度弹性加载板传递给钢管混凝土柱。
在网格划分方面,采用C3D8R实体单元对加载板及分割为规则几何形状后的混凝土进行结构化网格划分;外钢管采用S4R壳体单元进行结构化网格划分。为保证有限元模拟结果的精确性,设置初始网格尺寸为50 mm,逐步缩小进行多次试算,发现结构化网格尺寸缩小至20 mm以下时,构件极限承载力计算结果波动较小并趋于稳定,后文根据模型具体尺寸,取网格尺寸均为15 mm至20 mm,以综合考虑结果准确性与计算速度。
关于初始缺陷对RRCFST柱受压承载能力的影响,取初始偏心距e0予以考虑。已有学者证明一定取值范围内的偏心距e0=0,t/10,t,L/1 000对RRCFST短柱模型的分析结果影响均较小[8]。本文统一按照文献[15]中建议的初始偏心距e0=L/1 000以考虑RRCFST短柱及中长柱的初始缺陷影响。
模型各部件之间的相互作用方式如下:加载板与钢管、核心混凝土分别采用耦合(Coupling)、绑定(Tie)的作用方式;外钢管与核心混凝土之间法向接触采用硬接触(Hard Contact),切向接触采用惩罚性摩擦(Penalty)接触方式,摩擦因数取0.5[11]。加载线与其正上方的参考点耦合(Coupling),限制参考点水平方向平动和沿x,y方向转动,并通过在z方向施加位移的方式实现构件上边界约束与模型加载。完整模型的网格划分及加载示意如图3所示。

2.2 混凝土本构关系
模型中混凝土采用塑性损伤模型,流动偏心率取0.1,双轴等压强度与单轴强度比取1.225,黏性系数取1×10-5[16]。
基于圆端形钢管混凝土构件具有圆形及矩形构件的力学特点,现有研究已提出并使用了多种有限元建模方案,并在承载力方面取得了较好的预测结果。Ding等[7]运用钢管混凝土统一本构关系进行了有限元分析;Hassanein等[8]提出将核心混凝土部件分为圆端区域及矩形区域,分别使用对应的圆形钢管混凝土本构[17]与矩形钢管混凝土本构[18-19]以进行有限元建模分析,分区示意如图4所示;王静峰等[20]提出等效方法,根据圆端形截面高宽比将RRCFST构件等效为圆形或矩形钢管混凝土构件,再使用相应的圆形或矩形钢管混凝土本构关系进行有限元分析。

合理的混凝土本构关系选取决定着有限元模型的科学性与结果的准确性。上述相关学者的RRCFST构件研究表明,多种混凝土本构关系均可较准确预测RRCFST柱构件的极限承载力。经对比发现,在现有常用于RRCFST构件有限元分析的混凝土本构关系中,基于混凝土分区思想并使用圆角矩形及圆形钢管混凝土本构关系所得模型轴力-轴向应变曲线与试验曲线在全加载阶段拟合更好,其中使用混凝土分区模型的部分模拟曲线[4]与使用圆角矩形及圆形钢管混凝土本构关系[4]的模拟曲线如图5,6所示。

现根据文献[4]提出的分区建模思想,将模型混凝土构件的截面分为半圆形区域与矩形区域后,使用圆形、矩形钢管混凝土受压本构关系[4]进行有限元模拟分析。
2.2.1 圆形、矩形钢管混凝土本构关系
圆形、矩形钢管混凝土本构关系为
(1)
(2)
(3)

2.2.2 混凝土受拉软化本构
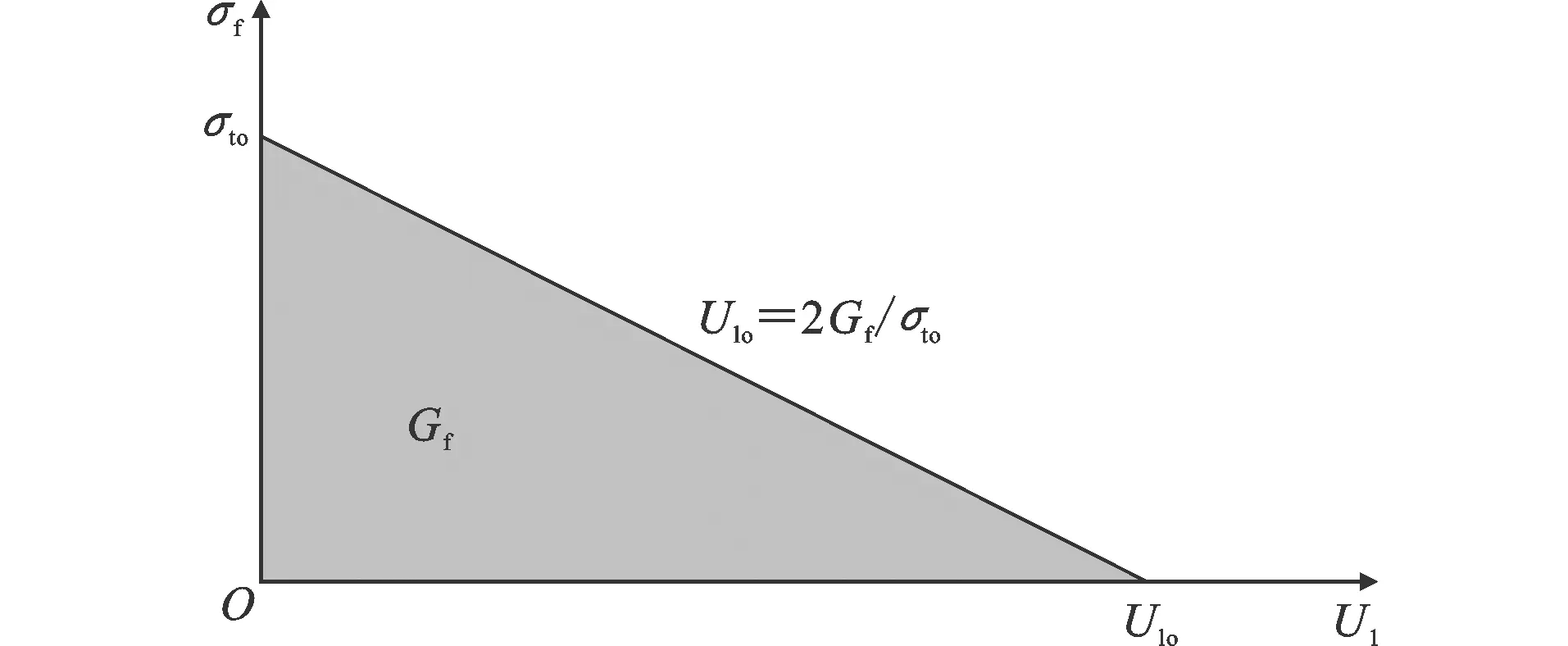
混凝土受拉软化本构采用沈聚敏等[21]的推荐公式计算,其本构关系曲线如图6所示(其中,σf和Ul分别为混凝土受拉应力和对应的裂缝宽度,σt0和Ulo分别为混凝土最大受拉应力和应力下降至0时对应的裂缝宽度,Gf为单位面积内产生一条连续裂缝所需要的能量),表达式为
(4)
针对不同的混凝土强度,σto和Ulo的关系有所不同,取决于Gf的取值。当混凝土强度为C20时,Gf=40 N·m-1,而对于C40混凝土,Gf=120 N·m-1,其他强度混凝土取线性插值计算[14]。
2.3 钢材本构关系
钢管的本构关系采用Von Mises屈服准则下的钢材弹塑性硬化本构模型[22],其表达式为
(5)
式中:σi,εi分别为钢材的等效应力及对应的应变;Es为钢材的弹性模量;fu为钢材的极限强度,取fu=1.5fy;ζ为强化系数;εy为钢材屈服时的应变;εst为钢材强化时的应变;εu为钢材达极限强度时的应变,εu=εst+0.5fy/(ζEs),取εst=12εy,εu=120εy,ζ=1/216。
3 模型验证
上述有限元方法分析得到各构件极限承载力Nu,0与试验结果对比如表1所示,其中最大偏差为7%,平均偏差为1%,表明上述建模方法对构件极限承载力预测结果良好。图7为有限元模拟加载曲线与试验实测加载曲线,由图7可知,使用钢管混凝土本构关系的模拟加载曲线与试验曲线吻合较好。证明该建模方法具有合理性与可靠性。

4 RRCFST偏压构件截面优化
实际偏压RRCFST柱设计中,经计算得到构件所承受的最不利荷载组合(轴向压力N,弯矩M)后,预设构件的材料强度fy,fcu及构件尺寸参数H,B,L,进而开展相应承载力验算及其他验算。若承载力验算不满足,则考虑增大构件尺寸、材料强度、变换截面高宽比等参数后重复上述步骤,直至满足要求。实际上,上述设计步骤缺少对材料使用效率的考虑:在承载力验算不通过进而考虑增大构件尺寸、材料强度时,可能忽略截面高宽比H/B变化对RRCFST构件承载能力的影响。
在材料强度及用量不变的条件下,通过改变RRCFST构件截面的高宽比H/B,即可改变构件所能承受的最大组合荷载(Nmax,Mmax)大小。通过细致研究截面高宽比H/B与构件所能承受的最大组合荷载(Nmax,Mmax)的关系,进而确定给定材料情况下不同截面高宽比的RRCFST柱构件所能承受的所有最不利荷载(N,M)的总和,即可达到基于材料强度及用量层面的RRCFST柱构件承载力快速验证、截面选优的目的,从而简化设计过程,并充分 发挥钢、混凝土材料组合受力效果,提高材料利用效率。
4.1 模型参数设计
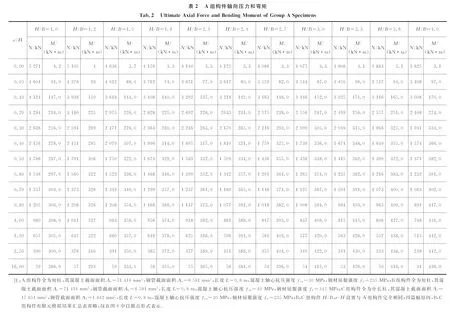
为细致研究截面高宽比对构件承载能力的影响,现设置A,B,C三组构件进行分析。每组均含有构件154个,且每组内各构件的材料用量(As,Ac)、材料强度(fcu,fy)、构件长度L作为基本参数保持相同,通过改变构件截面高宽比H/B及荷载偏心率e/H以探究截面高宽比H/B与构件极限组合荷载(Nmax,Mmax)的变化关系,具体构件参数及有限元模拟结果如表2所示。将表2结果汇总并以图形方式展示,如图8所示,其中A,B,C组构件长度L=0.8 m。A,B组模型的区别在于混凝土强度fcu、钢材屈服强度fy不同;A,C组模型的区别在于钢材用量及混凝土材料用量不同。

4.2 参数分析
目前各国家地区尚缺少计算RRCFST构件压弯承载能力的相关规范。对于圆端形钢管混凝土偏压构件的承载能力计算,文献[23]进行了大量的RRCFST偏压柱构件有限元模拟试验,验证了《钢管混凝土结构技术规范》(GB 50396—2014)[2]中CFST构件压弯承载设计模式对RRCFST偏压短柱构件设计的准确性与稳定性,本文不再作重复验证,其CFST构件压弯破坏曲线可根据式(6),(7)得到,但将其运用于RRCFST偏压短柱构件设计时,要注意将N0,M0及相关系数更换以适用于RRCFST构件。

(6)

(7)

对于N0,按以下经验公式取值[7]
(8)
对于M0,按以下经验公式取值[23]
M0=γmfscWsc
(9)
(10)
式中:γm为截面塑性发展系数;Wsc为受弯构件绕强轴的截面模量;fsc为实心钢管混凝土抗压强度设计值。
对比图8(a),(b)与图8(a),(c)可知,尽管A,B组构件之间具有不同的材料强度,A,C组构件之间具有不同的材料用量,其N-M曲线均可近似看作一段直线与一段抛物线组成,此结果也验证了式(6),(7)的破坏曲线特点。
4.2.1 截面高宽比与轴压承载力的关系
现分析破坏曲线的直线段部分,将图8中各曲线直线段部分单独取出,绘制成图9以方便分析总结。

将A,B,C组构件e=0(轴压荷载)情况下的有限元分析最大承载力相关结果绘制成图10(a)。可以看出,在截面高宽比H/B=1~4的范围内,随着截面高宽比H/B的增加,RRCFST构件的最大轴压承载力减小,且其变化速率变小。显然此结果与式(8)所反映的规律是一致的。

4.2.2 截面高宽比与破坏曲线直线段的斜率关系
由图10(b)各组构件直线段斜率散点拟合曲线可以看出,其直线段的斜率总为负值,随着截面高宽比的增大而增大,且增大速率变小。结合GB 50396—2014中直线段计算式,经变换得到斜率k为
(11)
不难看出,在各材料用量不变的条件下,RRCFST短柱偏压承载力有限元分析结果与上述设计模式中破坏曲线直线段斜率变化规律一致。
4.2.3 截面高宽比与N-M极限荷载曲线直线段右端点的关系
N-M极限荷载曲线直线段的右端点是N-M极限荷载曲线中的关键点,它是直线段与抛物线段的分界点,如图11(a)中的B点。为较全面地研究RRCFST柱构件破坏曲线直线段随截面高宽比H/B变化的特性,现将A,B,C三组构件各自近似直线段的B点取出,并绘制成图10(c)。可以看出,当截面高宽比H/B变化时,B点N随着弯矩M的增加而减小。
探究当截面高宽比H/B变化时B点在N-M曲线上的移动规律。根据式(6),对于直线
(12)
当取
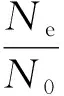
(13)
在直线段取得右部端点B。现将此条件及相关参数代入直线方程,得
(14)
显然,在各材料截面面积(Ac,As)、材料强度(fc,fy)不变的条件下,N0随着截面高宽比H/B的增大而减小,由此Ne随截面高宽比H/B的增大而减小。对于构件抗弯能力Me,由于Wsc随着截面高宽比H/B增大而增大,因此构件抗弯能力也增大。
以上为根据式(14)分析所得B点的运动轨迹,反映在N-M破坏曲线中即为一条单调递减的曲线,如图11(b)中的BC段曲线所示,其规律与图10(c)中有限元模拟结果一致。

通过上述分析方法结合文献[4]相关计算公式可知,矩形CFST短柱构件其轴压极限承载力与截面高宽比H/B无关,由此B点运动轨迹为一条水平的直线段,具体分析过程不再赘述。
4.3 破坏包络曲线
根据上述增大截面高宽比H/B与破坏曲线的变化特点,在给定材料强度(fc,fy)及材料用量(Ac,As)情况下,可定性绘制出固定柱长L的RRCFST偏压构件的N-M破坏包络图,如图11(c)所示。
直线AB段为截面高宽比H/B=1时对应的N-M破坏曲线直线段。曲线BC段为截面高宽比H/B由1增加至4时N-M破坏曲线直线段的右端点运动轨迹,曲线CD段为截面高宽比H/B=4时RRCFST短柱构件对应的N-M破坏曲线二次抛物线段。
以上定性绘制出了给定材料强度及用量情况下固定柱长的RRCFST偏压构件的N-M破坏包络图,其为材料强度及用量层面的破坏包络图,与具体RRCFST短柱构件的截面高宽比H/B无关。
4.3.1 基于材料强度及用量的破坏荷载包络曲线方程
图11(c)中A点对应为构件截面高宽比H/B=1时e=0的轴压破坏点,即A点纵坐标NA为轴压情况下圆形钢管混凝土柱的最大承载力,可通过式(8)取H/B=1得到。若将A点纵坐标记作NA,则可将其表示为
NA=N0=FRRCFST(Ac,As,L,fy,fc,μ,H/B=1)
(15)
式中:FRRCFST为轴压情况下圆端形钢管混凝土短柱构件的极限承载力;μ为考虑柱端约束条件的计算长度系数,按现行国家标准《钢结构设计标准》(GB 50017—2017)[24]取值。
图11(c)中B点为截面高宽比H/B=1的圆形钢管混凝土构件N-M破坏曲线直线段右端点。为方便标记,令
MRRCFST(Ac,As,L,fy,fc,μ,H/B)=M0
(16)
式中:MRRCFST为圆端形钢管混凝土柱主轴抗弯承载力。
结合式(8),则B点坐标(MB,NB)为
MB=MRRCFST(Ac,As,L,fy,fc,μ,H/B=1),
NB=2η0FRRCFST(Ac,As,L,fy,fc,μ,H/B=1)
(17)
可推导出直线AB段方程,令
ρAB(Ac,As,fy,fc,L,μ,M,N)=
(18)
则直线段AB方程(0 ρAB(Ac,As,fy,fc,L,μ,M,N)=1 (19) 对于曲线BC段,可根据变化截面高宽比H/B=1~4得到B点运动轨迹的参数方程,即 M=MRRCFST(Ac,t,L,fy,fc,μ,H/B) (20) N=2η0FRRCFST(Ac,t,L,fy,fc,μ,H/B) (21) 式中:1≤H/B≤4;MB 对于图11(c)中二次抛物线CD段,可取截面高宽比H/B=4对应的RRCFST偏压构件破坏曲线二次抛物线段,根据式(7)可得其曲线表达式为 (22) N0,D=FRRCFST(Ac,t,L,fy,fc,μ,H/B=4) (23) M0,D=MRRCFST(Ac,t,L,fy,fc,μ,H/B=4)=MC (24) 式中:b,c,βm按式(7)取值,且M>M0,D。 至此,推导得到N-M包络曲线各段的表达式为 (25) 对于圆形CFST柱构件,其截面形式固定,因此不存在材料强度及用量层面的三段式N-M破坏荷载包络曲线;对于矩形CFST柱构件,因其轴压极限承载力与截面高宽比无关的特性,其材料强度及用量层面的N-M破坏荷载包络曲线仍与截面高宽比无关,也不存在上述针对截面高宽比H/B的截面优化问题。 对于一般RRCFST偏压短柱构件设计,已知最不利荷载组合点(Me,Ne)与柱端部固定方式(μ),在预设材料用量及强度(Ac,t,L,fy,fc已知)时,可快速判断假定量的材料能否通过变换截面高宽比H/B以满足设计承载力要求。根据已知条件计算得到MB,MC,M0,D后进行判断。 若0 ρAB(Ac,As,fy,fc,L,μ,Me,Ne)≤1 (26) 若式(26)成立,则可直接取截面高宽比H/B=1以满足压弯承载力要求。 (27) 若MC≤Me,可直接取截面高宽比H/B=4,再对式(7)进行验算,若成立,则取截面高宽比H/B=4以满足压弯承载力要求。 若以上条件均不满足,则表明不存在某一截面高宽比H/B的RRCFST构件能够满足预设材料使用情况下的压弯承载要求,此时必须增加材料强度或材料用量并再次进行压弯承载力验算。 (1)在保证材料强度与材料用量不变的情况下,RRCFST构件的截面高宽比H/B越大,其N-M极限荷载曲线直线段右端点B的极限轴向承载力Ne变小,而极限抗弯承载力Me增大。 (2)基于GB 50396—2014中的CFST压弯构件设计模式,推导得到了一般设计过程中给定材料用量(As,Ac)及材料强度(fcu,fy)条件下针对RRCFST偏压短柱构件的破坏荷载包络曲线表达式,此材料强度及用量层面的包络曲线表达式与截面高宽比H/B无关。若以后有学者提出其他形式RRCFST构件轴压、纯弯等承载力计算公式,本文基于控制材料强度及用量恒定的包络曲线推导思想也可为相应的截面优化研究提供参考。 (3)基于所提出的RRCFST偏压短柱构件的破坏荷载包络曲线表达式,提出了快速判断给定材料下能否设计出满足承载力要求的RRCFST短柱构件的方法,并能够在材料足够的情况下直接计算确定RRCFST偏压短柱构件的截面高宽比H/B。由上述方法得到的截面高宽比H/B是精确值,所对应的截面为满足承载力要求的理论最佳截面,钢管厚度t、截面高度H、宽度B均为精确值,在实际工程设计中仍需要适当放大取整以便于施工。4.4 优化设计方法

5 结 语
