不平衡土压力对整体式桥台-H型钢桩-土体系力学性能影响试验
2021-07-21黄福云单玉麟严爱国陈宝春
黄福云,单玉麟,严爱国,桂 奎,陈宝春
(1. 福州大学 土木工程学院,福建 福州 350108; 2. 中铁第四勘察设计院集团有限公司,湖北 武汉 430063)
0 引 言
整体式桥台无缝桥(简称整体桥)是指上部结构的主梁、桥面板或桥头搭板和下部结构的桥台、台底桩基础连成整体共同吸收在温度或地震作用下主梁的伸缩变形[1-4]。整体桥由于较好的整体性、耐久性、抗震性和行车舒适性等优点被广泛应用于欧美等国[5-9],是一种可持续发展和全寿命周期的新型桥梁。最新颁布的《公路工程混凝土结构耐久性设计规范》(JTG/T 3310—2019)[10]建议150 m以内的桥梁可优先采用整体桥。
目前,国内外对整体桥桩基力学性能的研究主要集中在平衡土压力状态下。其中,Burdette等[11]、Ng等[12]、Huang等[13]和Guo等[14-18]分别开展了平衡土压力状态下预应力混凝土桩、PHC管桩、UHPC管桩和H型钢桩-土相互作用的研究,结果表明:平衡土压力状态下,桩身水平变形、桩侧土抗力和桩身弯矩基本上是对称的。研究也表明:预应力混凝土桩、PHC管桩、UHPC管桩和H型钢桩可以较好地适应整体桥上部结构的水平变形。H型钢桩因柔性好、变形能力强等优点在整体桥中的应用更广泛[19-23]。
然而,由于台后填土的存在,整体式桥台台底桩基础一般处于不平衡的土压力状态。黄福云等[24-27]首次开展了不平衡土压力下,整体式桥台-H型钢桩-土相互作用拟静力试验研究,结果表明:不平衡土压力下整体桥H型钢桩会产生正向累积变形现象,且桩身弯矩与传统理论计算方法存在较大的差异。王先前等[28]、刘钊[29]采用有限元分析了整体桥台后填土的影响,分析表明,在土体自重、车辆重载和振动荷载作用下会增加台后填土刚度,同时会减小桩顶水平位移。林友炜[30]采用有限元分析了整体桥台后不同填土类型的影响,研究表明,不同的填土类型对台后土压力的分布规律等会有较大的影响。由上述研究可知,台后不平衡土压力对整体桥桩基力学性能的影响较大。
由于车辆重载、台后填土压实度以及台后不同填料(砂或碎石)等作用下,将进一步造成台后不平衡土压力的变化(图1)。上述研究仅开展了较小不平衡土压力状态下整体桥桩基的力学性能研究。对于更大台后不平衡土压力对桩基力学性能影响的研究还较少,目前未有相关报道。
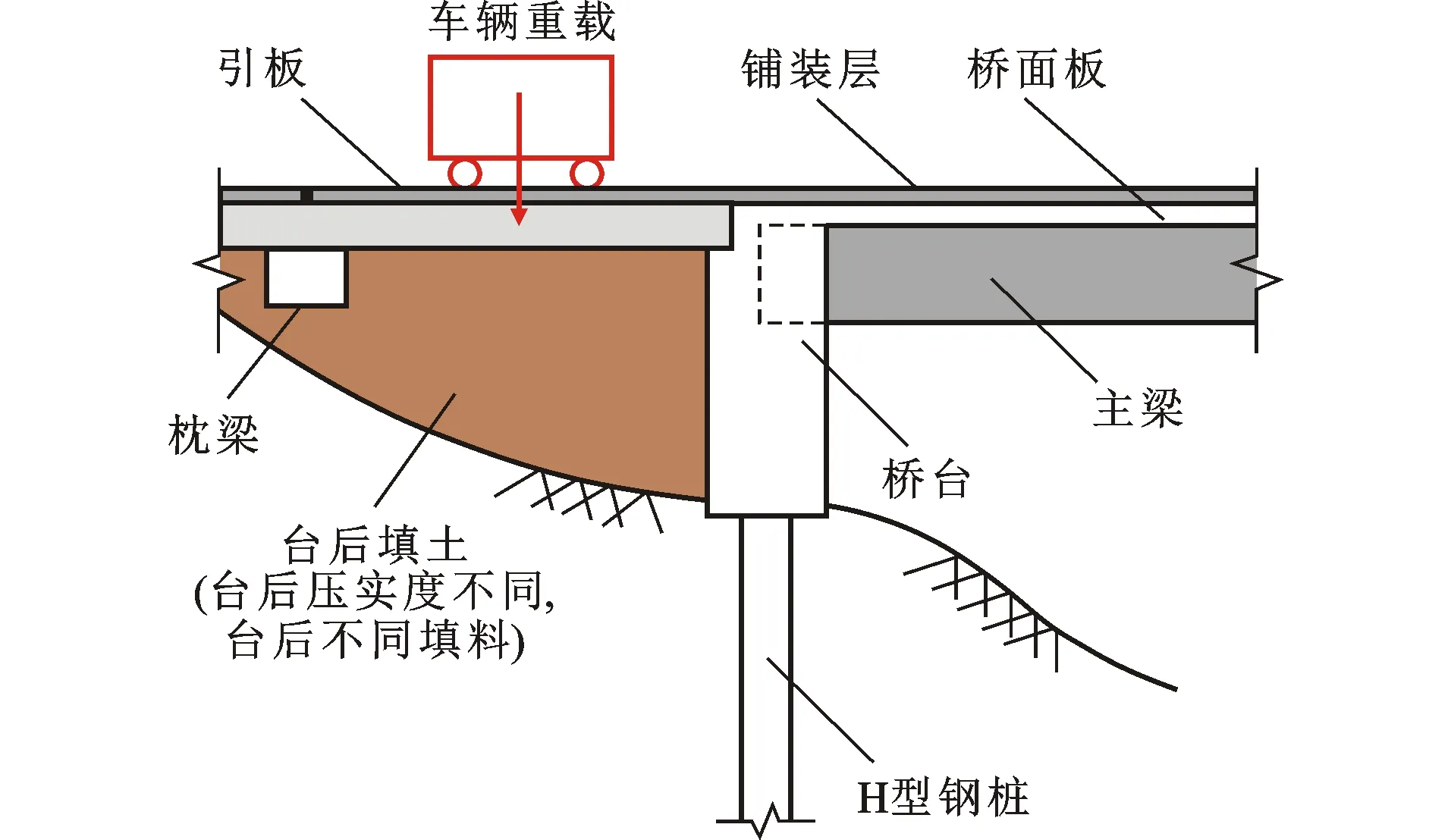
为此,本文在已开展的整体式桥台-H型钢桩-土相互作用拟静力试验研究的基础上[25-26],进一步开展更大不平衡土压力下(台后土表面均布荷载增大了3.81 kPa)整体式桥台-H型钢桩-土相互作用拟静力试验研究,分析对比更大不平衡土压力对桩身水平变形、桩侧土压力、应变和弯矩分布规律等方面的影响,为整体桥桩基设计和相关规范的制定提供借鉴和参考。
1 试验简介
1.1 试件设计
设计并制作了2个桥台-H型钢桩试件,编号分别为AHP和LAHP。其中,AHP试件为研究台后填土作用下整体式桥台-H型钢桩,这已在文献[25]中予以了介绍;本文着重介绍更大不平衡土压力下,整体式桥台-H型钢桩(LAHP),并与AHP进行比较。2个试件照片如图2所示。

试件采用缩尺比为0.31,与文献[25]一致,其中,桥台纵向宽度为660 mm,横向宽度为560 mm,高度为1 000 mm;H型钢桩长度L为3 210 mm,宽度B为155 mm,厚度W为217mm,翼缘板厚度t1和腹板厚度t2分别为6,10 mm。对于桥台-H型钢桩的连接,H型钢桩深入桥台0.31 m(2B),以满足桥台与H型钢桩固接要求[31]。
桥台竖向纵筋分别采用φ12与φ8的HRB335带肋钢筋,箍筋采用φ6的HRB335光圆钢筋。钢筋屈服强度为337 MPa,极限强度为454 MPa;H型钢桩均采用Q235钢材,抗压强度为fcu=215 MPa,屈服强度为fy=238 MPa,弹性模量为E=1.86×108Pa。
1.2 土 箱
土箱采用长3 m、宽2 m、高4 m、壁厚10 mm的刚性矩形钢箱。该土箱可使桩基满足5倍桩径距离的要求[32-34],桥台满足2倍桥台高度的要求[35],可忽略土箱边界效应的影响。
试验用砂采用闽江砂土。从土箱压实的砂土中环刀取多个试样,在室内实验室测量砂土的参数。经试验测得该砂属于稍密砂,密度为1.50 g·cm-3,相对密度为53%,内摩擦角为35°,含水率为1.3%,孔隙比为0.8,黏聚力为0 kPa,平均标准贯入度为11。
1.3 不平衡土压力
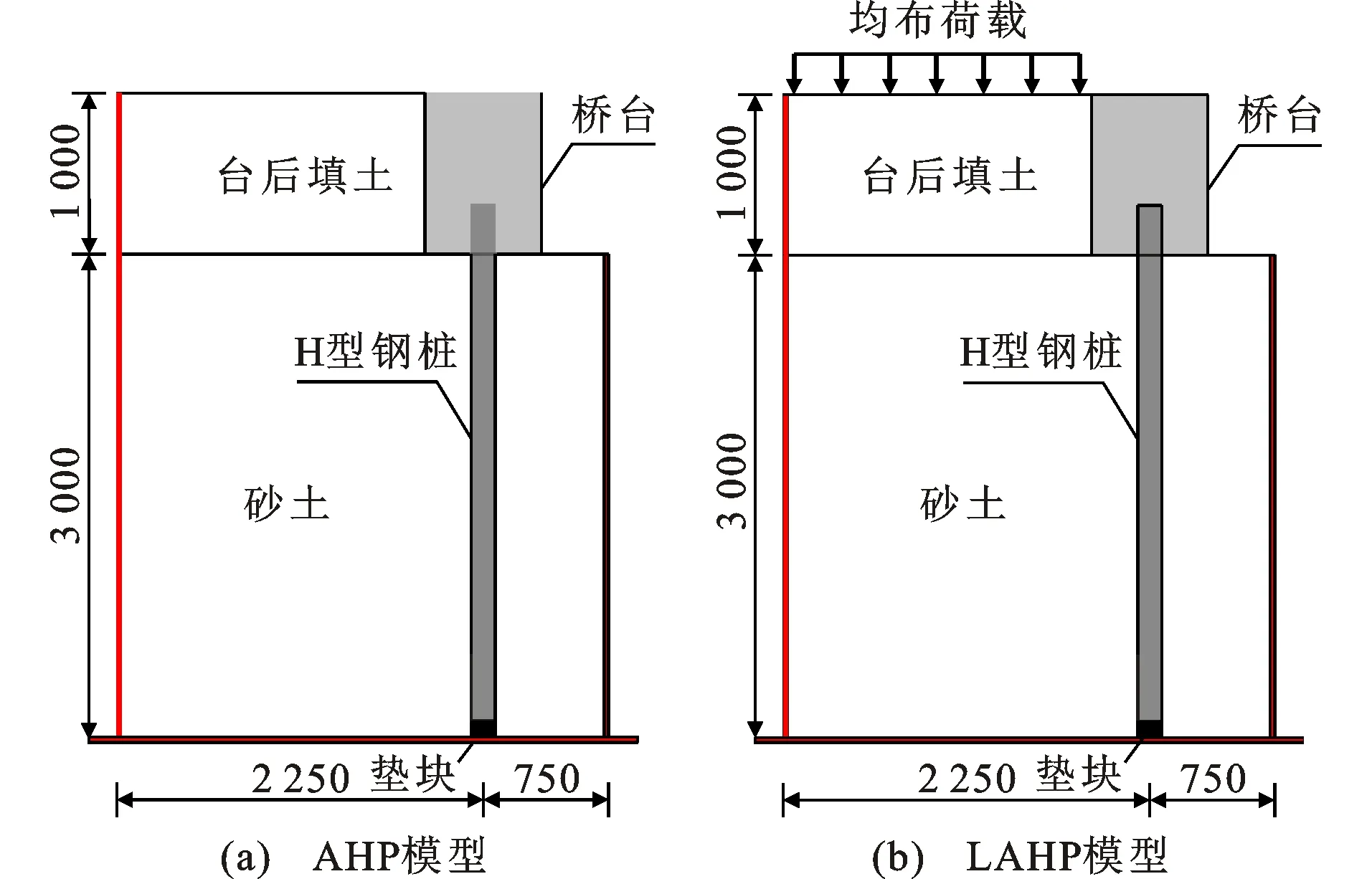
图3(a)为文献[25]开展的台后填土作用下整体式桥台-H型钢桩-土相互作用试验(AHP试件)。为了进一步研究更大不平衡土压力对整体式桥台下H型钢桩力学性能的影响,在图3(a)的基础上,LAHP模型通过采用质量块的形式施加均布荷载来模拟车辆重载、填土压实度或不同填料(砂或碎石)等引起的不平衡土压力。质量块重约2.5 t(15 kN),均匀施加在台后填土上,如图3(b)所示。
1.4 测点的布置
LAHP模型布置有应变片、土压力计和位移计。对于应变片的布置,在LAHP模型H型钢桩两翼缘对称布置13对应变片,共计26个,从土表面开始以200 mm为间距进行布置,编号为S1~S26,如图4(a)所示。对于土压力计的布置,在LAHP模型H型钢桩腹板对称布置10对土压力计,共计20个,从土表面开始分别以200 mm和400 mm为间距进行布置,编号为T1~T20,如图4(b)所示。对于位移计的布置,在LAHP模型桥台台顶和台顶下700 mm布置2个位移计,编号为D1,D2;在H型钢桩布置11个位移计,从桩顶开始间距分别为200 mm和600 mm,编号为D3~D13,如图4(c)所示。

1.5 试件加载
拟静力试验采用福州大学MTS电液伺服加载系统施加低周往复水平位移荷载。与文献[25]一致,LAHP模型作动器作用点距台顶0.35 m,如图5(a)所示。
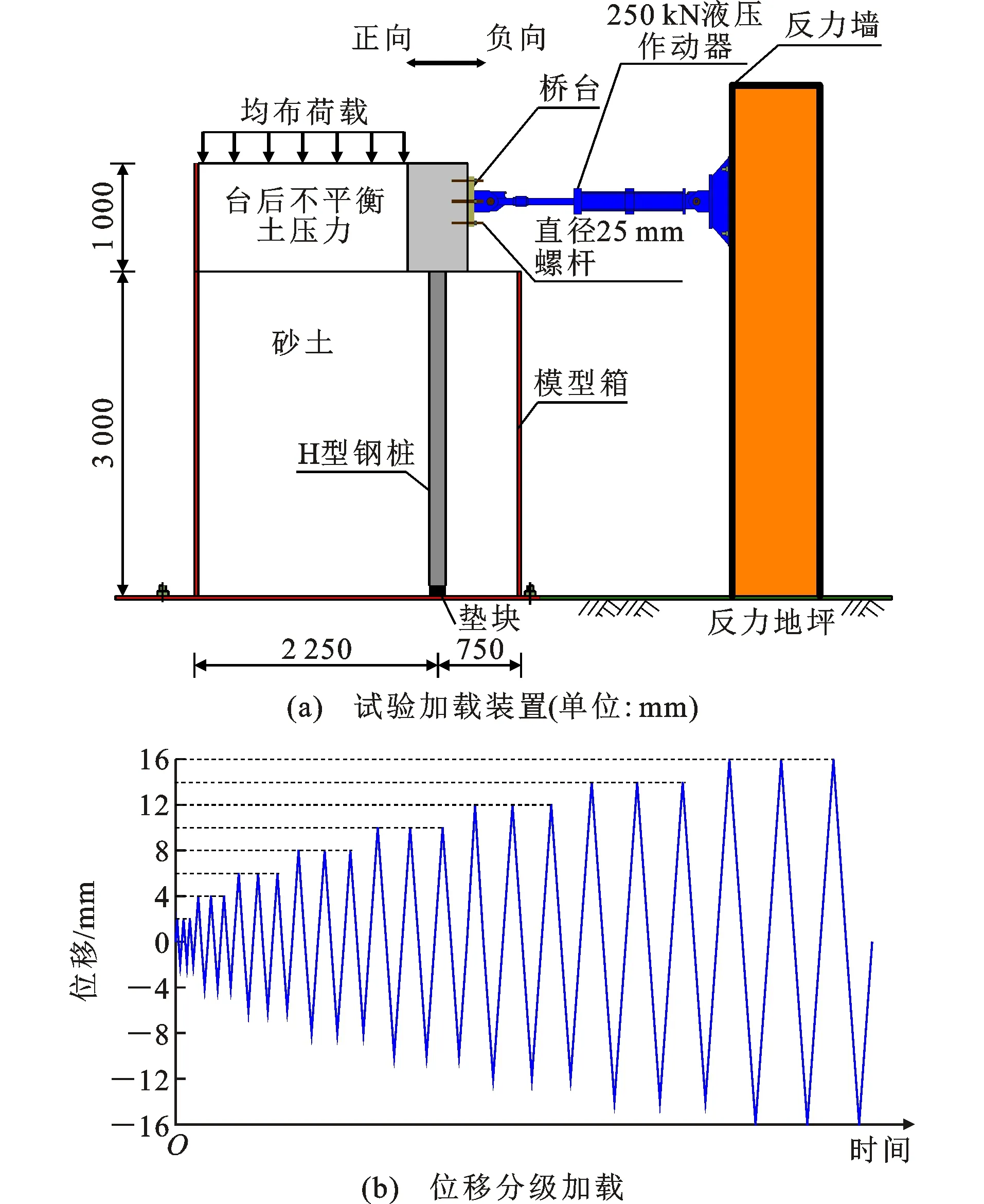
试验过程中采用位移控制分级加载。每级以2 mm的位移为增量逐级加载,加载至16 mm终止,加载频率为1 Hz, 每级荷载循环3次,且每级加载持荷30 s,如图5(b)所示。如无特殊说明,均取每级荷载第2次循环的试验结果进行分析。本文定义往台后土方向施加位移荷载为正方向,往河跨方向施加为负方向。
2 试验结果分析
2.1 桩身水平变形分析与比较
2.1.1 桩身水平变形分析
图6为LAHP模型沿深度方向的桩身水平变形分布规律。从图6(a)可以看出:正向加载时,LAHP模型在埋深0.0~0.8 m(0.0~5.2B)范围内,桩身水平变形方向与加载方向一致,位于桩后侧,以埋深0.6 m(3.9B)处最大,最大值为+14.37 mm;超过埋深0.8 m后桩身变形与加载方向相反,位于桩前侧,以埋深1.2 m(7.7B)最大,最大值为-2.41 mm。

从图6(b)可知,除桩顶0.0~0.4 m(0.0~2.6B)范围内不一样外,负向加载时的桩身水平变形与正向加载时的基本一致。
2.1.2 桩身水平变形比较
图7为位移荷载为±16 mm时AHP和LAHP模型桩身水平变形的比较。从图7可知,正、负向加载时,AHP和LAHP模型桩身水平变形分布规律基本相似。更细地比较可知,LAHP模型桩身累积变形的位置更深,分析其原因是因为正向加载时,在更大不平衡土压力作用下,台后土体自台底向前到桩前侧流动的土体更多,并填充桩前侧桩-土脱空区域,使得桩前土体更加密实,进而造成累积变形的位置更深。另外,正向加载时,LAHP模型的桩身累积变形比AHP模型小,负向加载则相反。

2.2 桩侧土抗力分析与比较
2.2.1 桩侧土抗力分析
图8为LAHP模型沿深度方向的桩侧土抗力分布规律。从图8(a)可知:正向加载时,在埋深0.0~0.4 m(0.0~2.6B)范围内,LAHP模型桩侧土抗力沿埋深方向增至最大;在埋深0.4~1.6 m(2.6B~10.3B)范围内,逐渐减小;在埋深1.6~2.9 m(10.3B~18.7B)范围内,反向逐渐增大。从图8(b)可知:负向加载时,在埋深0.0~1.0 m(0.0~6.5B)范围内,LAHP模型桩侧土抗力沿埋深方向逐渐增大;在埋深超过1.0 m(6.5B)处,桩前土抗力逐渐减小。

比较图8(a),(b)可知,由于台后不平衡土压力的影响,LAHP模型正向加载时的桩侧土抗力显著大于负向加载时的。当位移加载为±16 mm时,正向最大桩侧土抗力为45.09 kPa,对应埋深为0.4 m(2.6B);负向桩侧土抗力为20.09 kPa,对应埋深为1.0 m(6.5B);前者是后者2.2倍,且前者最大土抗力埋深稍浅。
2.2.2 桩侧土抗力比较
图9为正向位移加载为+16 mm时,AHP和LAHP模型桩侧土抗力的比较。从图9可知,正向加载时,AHP和LAHP模型桩侧土抗力分布规律 基本相似。不过,由于更大不平衡土压力的影响,LAHP模型桩后侧最大土抗力更大,同时最大土抗力对应的埋深也更深。如LAHP和AHP模型桩侧最大土抗力分别为45.1 kPa和35.6 kPa,对应埋深分别为0.4 m(2.6B)和0.2 m(1.3B);前者最大桩侧土抗力是后者的1.3倍。由于负向加载时AHP和LAHP模型桩侧土抗力大小和分布规律基本相似,限于篇幅,本节未给出负向加载时的比较。

2.3 桩身应变和弯矩分析与比较
2.3.1 桩身应变和弯矩分析
图10为LAHP模型沿深度方向的桩身拉、压应变和弯矩分布规律。从图10(a)可知,正向加载时,LAHP模型桩身拉、压应变和弯矩基本上沿埋深方向逐渐减小。桩身拉、压应变不对称。如桩身最大拉、 压应变埋深分别为0.0 m和0.2 m(1.3B)处;桩身最大拉、压应变分别为1 206.51×10-6和-763.93×10-6,接近弹性极限应变。从图10(b)可知,负向加载时,LAHP模型桩身拉、压应变和弯矩沿埋深方向先增大后减小。桩身最大拉、压应变分别为583.31×10-6kPa和-362.31×10-6kPa,均处于弹性范围内。另外,桩身最大拉应变埋深为1.0 m(6.5B),压应变埋深为0.8 m(5.2B),前者略浅于后者。

比较图10(a),(b)可知,正、负向加载时,LAHP模型桩身应变和弯矩分布规律均存在显著的差异。分析其原因是由于台后不平衡土压力的影响,使得LAHP模型正向加载时桥台产生的桩顶弯矩要远大于负向加载时桥台产生的桩顶弯矩,进而使得该区域的桩身应变急剧增加,导致不一样的分布规律。同时,正向加载时的桩身应变和弯矩显著大于负向加载时的。如正向加载时桩身最大弯矩为13.92 kN·m和对应埋深为0.4 m(2.6B);负向加载时桩身最大弯矩为6.72 kN·m和对应埋深为1.0 m(6.5B);前者为后者的2.1倍,且前者最大桩身弯矩埋深稍浅。
2.3.2 桩身弯矩比较
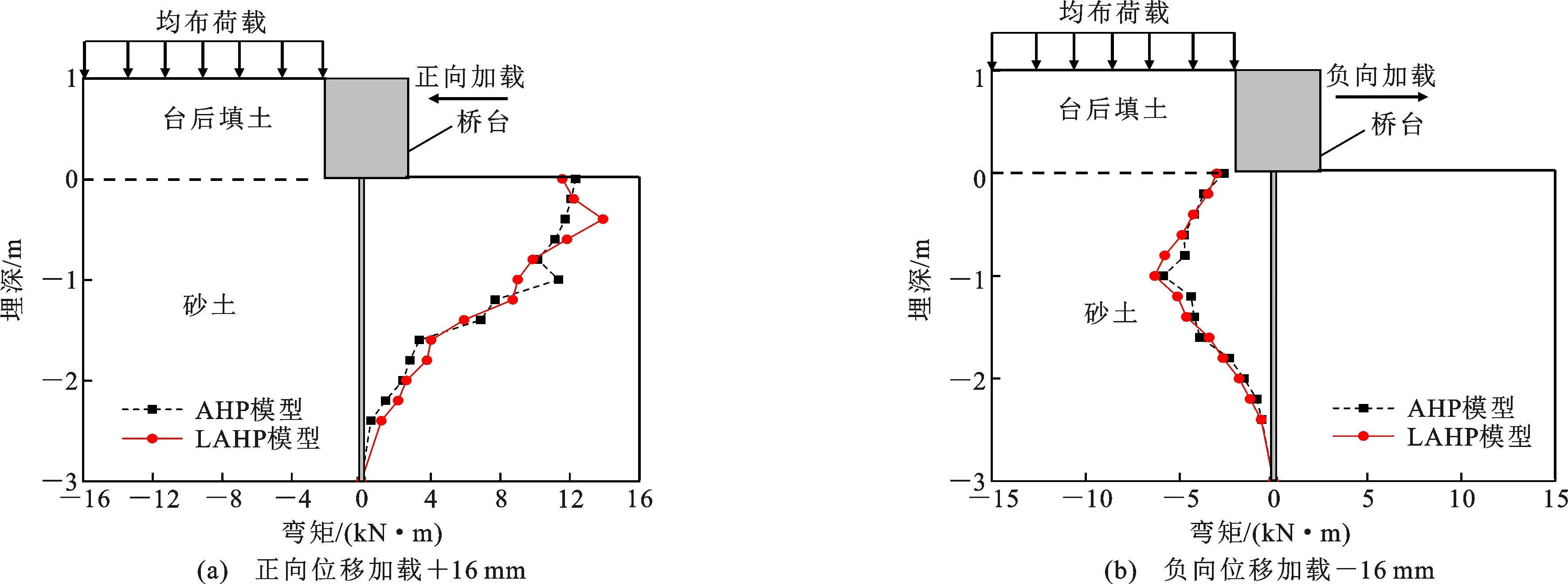
图11为位移荷载为±16 mm时,AHP和LAHP模型桩身弯矩的比较。从图11可知,正、负向加载时,AHP和LAHP模型桩身弯矩分布规律基本相似,但LAHP模型桩身弯矩比AHP模型略大。更细地比较可知,正向加载时,LAHP和AHP模型最大弯矩分别为13.9 kN·m 和12.3 kN·m,对应埋深分别位于0.4 m(2.6B)和0.0 m处,前者最大弯矩为后者的1.1倍,且前者最大弯矩埋深较深;负向加载时,LAHP和AHP模型的最大弯矩分别为6.7 kN·m 和6.2 kN·m,对应埋深均位于1.0 m(6.5B),前者最大弯矩为后者的1.1倍。
3 结 语
(1)更大不平衡土压力对桩身水平变形、土抗力、应变和弯矩的分布规律无影响。
(2)正、负向加载时,更大不平衡土压力均使得累积变形的位置更深。另外,正向加载时,更大不平衡土压力使得累积变形减小;负向加载时则相反。
(3)正向加载时,更大不平衡土压力使得桩侧最大土抗力更大和对应埋深更深,负向加载时则相差不大。
(4)正、负向加载时,LAHP模型桩身拉、压应变和弯矩存在显著的差异。另外,更大不平衡土压力使得桩身内力有所增加。
(5)正向加载时,LAHP模型的桩侧土抗力、应变和弯矩显著大于负向加载时的。如正向加载时的桩侧土抗力和弯矩分别为负向加载时的2.2倍和2.1倍。
