局部减薄管道极限弯矩计算新公式
2021-07-21李祚成李思源
李祚成,李思源,许 可
(1.机械工业上海蓝亚石化设备检测所有限公司,上海 201518;2.兰州石油机械研究所有限公司,甘肃 兰州 730050;3.中石油 云南石化有限公司,云南 昆明 650300)
压力管道,特别是海底管道,由于使用环境复杂、管道承受的载荷复杂、管道的应力状态复杂,因此管道剩余强度的评估也是一个复杂的课题。近半个世纪以来,国际上对管道剩余强度评估开展了许多的硏究工作,其中Bouwkamp J G等[1]和Sherman D R[2]对无缺陷管道在联合载荷下的极限承载力进行了大量的数值分析和实验硏究。基于塑性失效理论,釆用理想弹塑性本构模型,Mohareb M等[3-8]提出了无缺陷管道在内压、轴向力和弯矩联合载荷下的极限承载力解析解,并与实验结果进行比较,得出该简化方法能很好地预测管道极限承载力。之后Bai Y等[9-12]将这部分工作扩展到了腐蚀管道,将管道腐蚀形状简化为减薄深度在环向不发生变化,分别针对4种不同工况的等深减薄管道提出了极限弯矩计算方法。该方法已经被ABS的 《Guide for Building and Classing Subsea Pipeline System》[13]采用,用于评估腐蚀海底管道剩余强度。文献[14-15]也釆用Hill屈服准则,推导了不规则腐蚀缺陷管道在内压、轴向力和弯矩联合作用下极限承载力的广义计算公式。但笔者认为,文献[9-15]中提出的当管道进入全塑性状态时,管道横截面压应力极限值 σcomp(或 σc)和拉应力极限值 σtens(或σt)的计算式值得进一步探讨。
本文针对承受内压p、轴向力F和弯矩M联合作用的局部减薄管道,应用屈服准则,给出了管道横截面弯曲压缩侧应力极限值和弯曲拉伸侧应力极限值的计算式,导出了内压p和轴向力F必须满足的条件。并釆用理想弹塑性本构模型,推导了含等深减薄管道在联合载荷作用下极限弯矩计算的新公式,证明了文献[9-15]中极限弯矩计算式的理论依据不充分。
1 局部减薄管道极限弯矩计算基本理论
1.1 基本假定和简化
(1)不考虑管道钢材应变强化作用,釆用理想弹塑性应力-应变本构关系。
(2)在管道达到全塑性状态前,管道的横截面形状不发生改变。
(3)在管道达到极限状态时,塑性中性轴将管道横截面分为弯曲压缩和弯曲拉伸2个区域,管道截面达到相应的全塑性状态。
1.2 局部减薄管道屈服准则
设管道的外半径为Ro,管壁厚度为t,平均半径 Rm=Ro-t/2,管道内壁存在深度为 d、环向截面夹角为2β的等深减薄缺陷 (图1),其轴向长度很长。
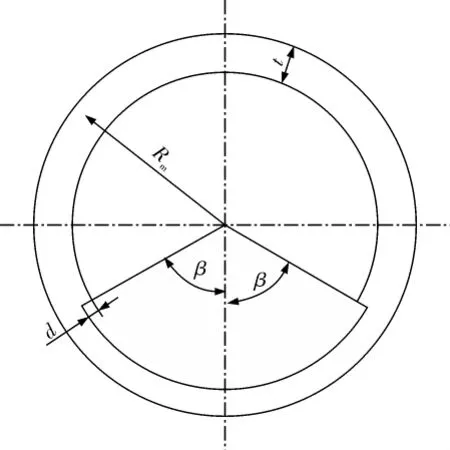
图1 含等深减薄管道横截面几何尺寸示图
对于各向异性材料的管道,在内压p、轴向力F和弯矩M联合作用下发生屈服时,釆用Hill屈服准则可以得到:

式中,σz为管道轴向应力,σθ为管道环向应力,σzl为管道材料轴向屈服应力,σθl为管道材料环向屈服应力,MPa;α为各向异性系数,一般取α=σθl/(2σzl)[14]。
求解式(1)得到管道轴向应力σz的解:

1.3 管道屈服的轴向极限应力
在内压p、轴向力F和弯矩M联合作用下,含等深减薄管道的环向应力σθ由内压p、且只由内压p产生,内压p对该管道产生的轴向力Fp为轴向力F的组成部分。管道的轴向应力σz只由轴向力F和弯矩M产生。
1.3.1 等深减薄部位
在管道减薄深度为d的部位,管道的环向应力σθd由内压p产生,且近似为:
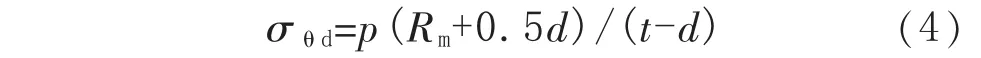
当管道减薄深度为d的部位处于弯曲压缩侧时,将式(4)代入式(3),得到该部位屈服的轴向应力极限值σcd:

当管道减薄深度为d的部位处于弯曲拉伸侧时,将式(4)代入式(2),得到该部位屈服的轴向应力极限值σtd:
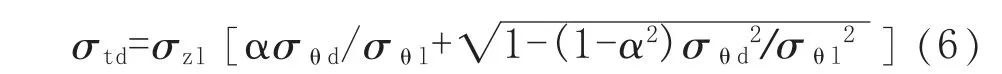
1.3.2 未减薄部位
在管道未减薄部位,管道的环向应力σθ0由内压p产生,且近似为:
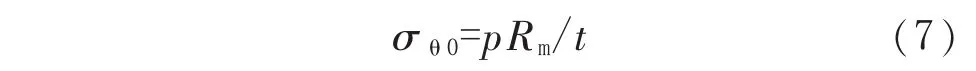
当管道未减薄部位处于弯曲压缩侧时,将式(7)代入式(3),得到该部位屈服的轴向应力极限值 σc:

当管道未减薄部位处于弯曲拉伸侧时,将式(7)代入式(2),得到该部位屈服的轴向应力极限值 σt:

1.3.3 极限应力不等式
当管道内压p>0,管道等深减薄深度d>0时,极限应力σcd和σc满足不等式:

下面对式(10)进行证明。 由式(4)和式(7)可以得到:

计及式(11),则有 v0-vd=(1-α2)(σθd-σθ0)×(σθd+σθ0)/σθl2>0,因此有:
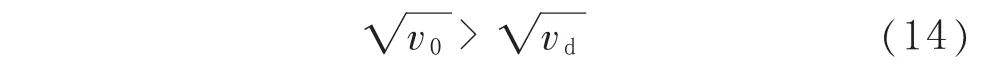
根据式(11)和式(14),由式(5)和式(8)可以得到:

由此可以证明式(10)成立。
2 等深减薄管道极限弯矩计算
2.1 等深减薄管道承载弯矩的条件
含等深减薄管道横截面的面积 S(d,β)用式(16)计算:

管道在内压p和轴向力F联合作用下,管道的轴向应力σz近似为:
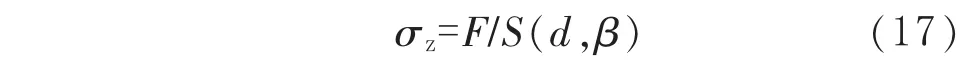
其中内压p产生的轴向载荷包含在轴向力F当中。

含等深减薄管道在内压p和轴向力F联合作用下,用式(4)计算减薄区的环向应力 σθd,用式(7)计算未减薄区的环向应力 σθ0,用式(18)计算Fl。该管道承载弯矩的条件是 σθd、σθ0和 F同时满足以下不等式:
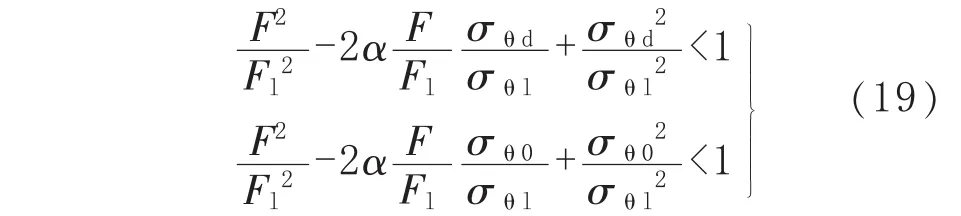
对式(19)进行证明。等深减薄管道在内压p和轴向力F联合作用下,管道产生的轴向应力σz可用式(17)近似计算,再应用式(18)得到:
亚行预计,气候变暖在经济方面将带来负面影响。东南亚等国家如不及时采取措施,到本世纪末,气候变化每年给相关国家带来的经济损失将超过GDP的5%以上,全球的GDP将下降2.8%,印度尼西亚、菲律宾将下降6.7%,比全球平均数高得多。相反,到2020年,若东南亚等国家增强应对全球气候变化措施,增强能力建设,相应地投入一些成本,那么获得的利润比投入的成本要高得多。

管道减薄区产生的环向应力σθ=σθd,应用式(20)有:

再利用式(19)中的第1式,得到在管道的等深减薄区都满足:

管道未减薄区产生的环向应力σθ=σθ0,应用式(20)得到:
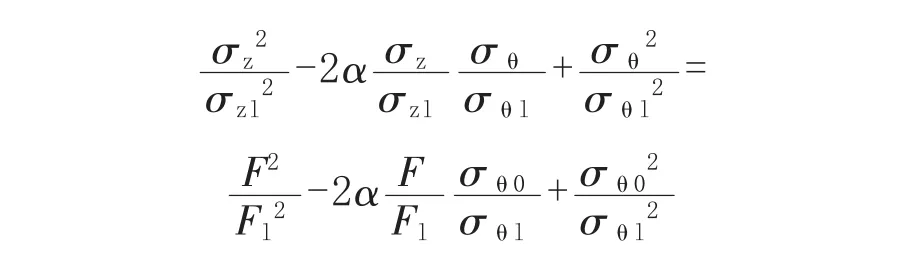
再利用式(19)中的第 2式,得到式(21)在管道的未减薄区也成立。
因此,等深减薄管道在内压p和轴向力F联合作用下没有屈服,该管道还可以承载一定的弯矩载荷。
2.2 等深减薄管道极限弯矩计算新公式
2.2.1 计算工况
根据承载弯矩的条件,计算等深减薄管道在内压p、轴向力F和弯矩联合作用下的极限弯矩时,由内压p产生的环向应力σθd、σθ0和轴向力F必须同时满足式(19)。又设管道横截面弯曲的塑性中性轴夹角为ψ,考虑塑性中性轴位置,可按图2所示的4种工况计算管道的极限弯矩。其中工况1的β<ψ1,减薄区全部在弯曲压缩区;工况2的β>ψ2,减薄区部分在弯曲压缩区,部分在弯曲拉伸区;工况3的β<ψ3,减薄区全部在弯曲拉伸区;工况4的β>ψ4,减薄区部分在弯曲拉伸区,部分在弯曲压缩区。在工况1和工况2中,塑性中性轴下方为弯曲压缩区;在工况3和工况4中,塑性中性轴下方为弯曲拉伸区。

图2 含等深减薄管道4种极限弯矩计算工况
工况1下等深减薄管道横截面理想应力分布见图 3。
当管道在内压p和轴向力F作用下,再逐步施加弯矩载荷,使该管道横截面每一处的应力(σz,σθ)逐步达到屈服条件(式(1))。 根据基本假定,釆用理想弹塑性应力-应变本构关系,且不考虑应变强化作用,弯曲载荷使管道横截面在弯曲的塑性中性轴两侧逐步达到屈服极限状态,最后使横截面达到全塑性状态。又由于工况1的管道减薄区全部在弯曲压缩侧,因此塑性中性轴在截面未减薄区,且工况1中的塑性中性轴和截面减薄段两端点的连线将该横截面划分为3个极限屈服应力区,即图3中的Ⅰ区、Ⅱ区和Ⅲ区。等深减薄管道在4种工况中的参量见表1。
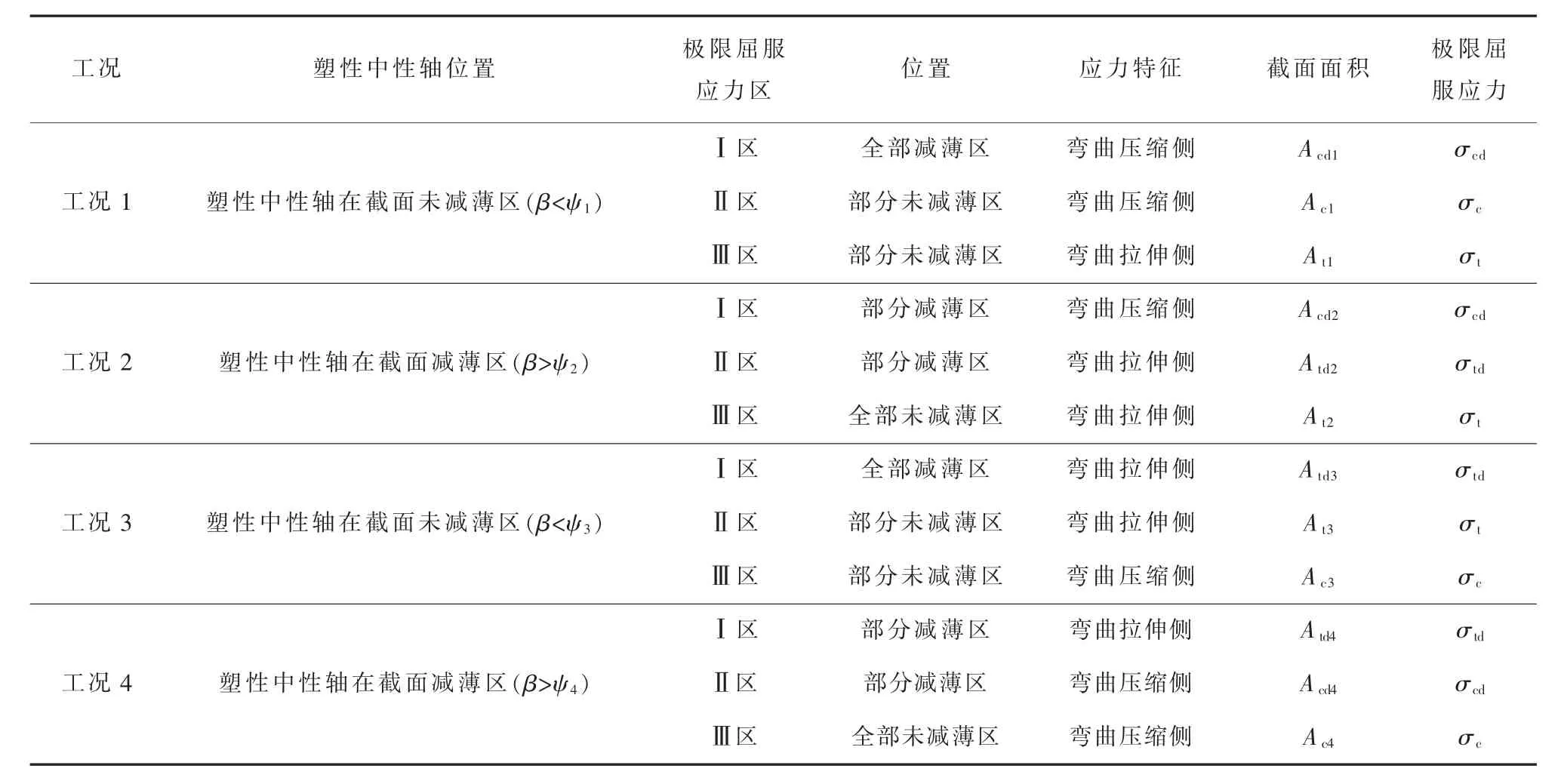
表1 等深减薄管道在4种工况中的参量

图3 工况1下等深减薄管道横截面理想应力分布
在工况1下,轴向力F可近似表示为:
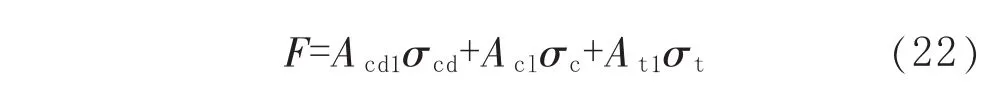
Acd1、Ac1和At1分别为图3中Ⅰ区、Ⅱ区和Ⅲ区对应的面积,且 Acd1=2βk1Rmt、Ac1=2(ψ1-β)Rmt、At1=2(π-ψ1)Rmt,k1按下式计算:

将 Acd1、Ac1和 At1的计算式代入式 (22),得到塑性中性轴夹角ψ1的计算式:

当式(24)的计算值 ψ1>β 时,减薄管道的极限弯矩 M1(p,F)可表示为:
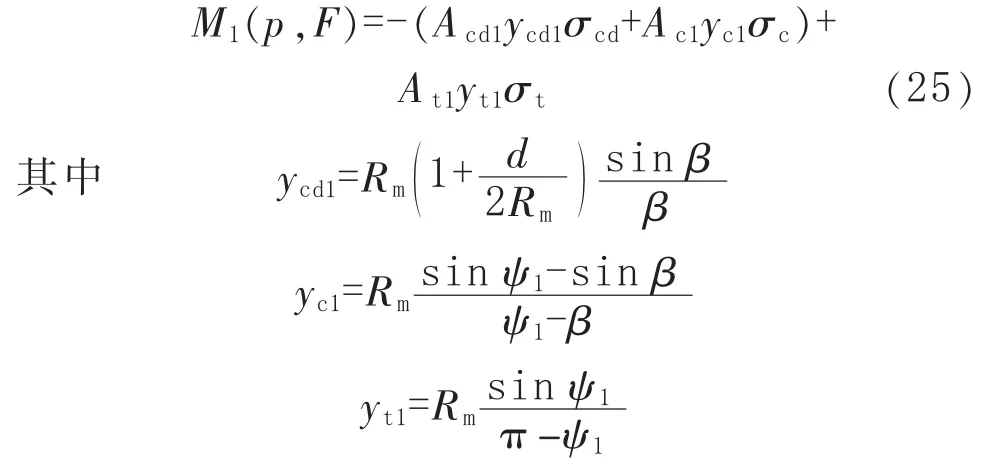
将 ycd1、yc1、yt1计 算 式 和 相 关 各 式 代 入 式(25),得到工况1下减薄管道的极限弯矩M1(p,F)计算式:

2.2.3 工况2计算公式
在工况2下,当管道达到全塑性状态时,轴向力F可近似表示为:

Acd2、Atd2和At2分别为对应极限屈服应力区域的面积, 且有 Acd2=2k1ψ2Rmt、Atd2=2k1(β-ψ2)×Rmt、At2=2(π- β)Rmt。将 Acd2、Atd2和 At2的计算式代入式(28),得到塑性中性轴夹角ψ2的计算式如下:

当式(29)的计算值 ψ2<β 时,减薄管道的极限弯矩 M2(p,F)可表示为:
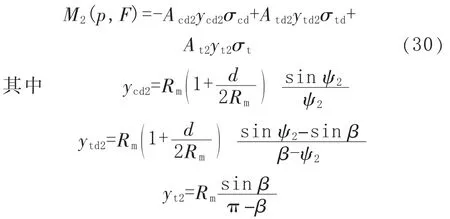
在工况 2下,管道的极限弯矩 M2(p,F)计算式为:
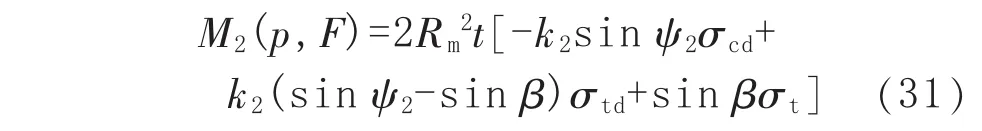
2.2.4 工况3计算公式
工况3下,塑性中性轴夹角ψ3计算式为:
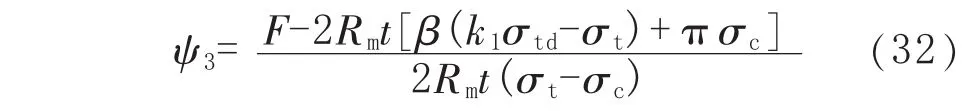
管道的极限弯矩 M3(p,F)计算式为:

2.2.5 工况4计算公式
工况4下,塑性中性轴夹角ψ4计算式为:

管道的极限弯矩 M4(p,F)计算式为:

3 几种局部减薄管道极限弯矩计算式讨论
3.1 文献[9-13]
上述建立的局部等深减薄管道极限弯矩计算新公式与文献[9-12]中推导的计算式有很大差别。以文献[9]为例,设σy为管材的屈服强度,Mises屈服准则为:

由Mises屈服准则导出了管道横截面轴向压应力极限值σcomp和轴向拉应力极限值σtenr,即为文献[9] 中的式(3)和式(4):

式(39)可参见文献[9]中的式(5)。 可以看出,当 p>0时,由式(39)确定的环向应力 σθ等于管道等深减薄区内由内压p产生的环向应力 (式(4))。 因此由式(37)、式(38)确定的应力值 σcomp、σtenr在管道的等深减薄区满足式 (36)的Mises屈服准则。但是管道未减薄区内由内压p产生的环向应力(式(7))不同于式(39)计算结果。因此,用式(39)的 σθ计算的 σcomp、σtenr在管道未减薄区域就不一定满足Mises屈服准则。这样,文献[9]中式(5)之后推导的管道极限弯矩计算式的理论依据就不够充分。只有当p=0时,则σθ=0、σcomp=-σy、σtenr=σy,文献[9]中推导的管道极限弯矩计算式才成立。
文献[10-12]中也存在类似于文献[9]的问题。文献[13]第109页最大允许弯矩Mall的计算式是采用文献[11]的弯矩计算式,因此该计算式也值得商榷。
3.2 文献[14-15]
文献[14-15]釆用Hill屈服准则硏究腐蚀管道极限承载力,由式(1)得到式(2),当管道进入全塑性状态时,管道横截面轴向压应力极限值σc和轴向拉应力极限值σt为:

为了计算方便,也可以表示为:
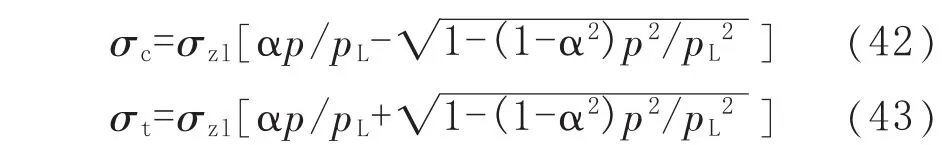
式中,pL为无缺陷管道的极限内压,并且有pL=σθlt/Rm。
文献 [14-15] 中对式 (40) 和式 (41)取σθ=pRm/t,又计及 pL=σθlt/Rm,就得到了式(42)和式(43),即文献[14-15]中的计算式(5)和式(6)。因此,式(42)和式(43)在管道未腐蚀区域满足Hill屈服准则。但在腐蚀区域内,其剩余壁厚tθ<t,因此管壁tθ处由内压 p产生的环向应力 σθ一般都有 σθ>pRm/t,式(42)和式(43)计算的 σc、σt在腐蚀区就不一定满足Hill屈服准则。这样文献[14-15]中式(5)和式(6)之后推导的管道极限弯矩计算式的理论依据就不充分。只有当p=0时,则 σθ=0、σc=-σzl、σt=σzl,文献[14-15]中推导的管道极限弯矩计算式才成立。
4 不同方法计算管道极限弯矩案例分析
4.1 计算案例
设管道的平均半径Rm=500 mm,管壁厚t=20 mm。管道钢管轴向和环向极限应力σzl=σθl=500 MPa,各向异性系数α=0.5。设管道橫截面内壁等深减薄深度 d=10 mm,环向减薄夹角 2β=π(图 1),其轴向长度很长。减薄区位于管道弯曲压缩侧。
该管道承受载荷为内压p和轴向力F(F值中已包括内压p产生的轴向力),其载荷1的p=10 MPa、F=23 000 kN, 载 荷 2 的 p=10 MPa、F=500 kN,载荷 3 的 p=7 MPa、F=-10 000 kN。采用3种方法计算管道在载荷1下的极限弯矩。
4.2 计算方法
4.2.1 本文方法
在管道减薄部位,应用式 (4)得到由内压p=10 MPa产生的环向应力 σθd=505 MPa,由式(5)和式 (6)得到管道减薄区的轴向应力极限值σcd=10.15 MPa、σtd=494.85 MPa。
在管道未减薄部位,应用式 (7)得到内压p=10 MPa产生的环向应力 σθ0=250 MPa,由式(8)和式 (9)得到管道减薄区的轴向应力极限值σc=-325.69 MPa、σt=575.69 MPa。
由式(16)和式(18)得 Fl=23 640.5 kN。 因此,F=23 000 kN、σθd=505 MPa 和 σθ0=250 MPa 满足管道承载弯矩的条件,即式(19)。
由式(23)和式(27)得 k1=0.505、k2=0.510,由式(29)得塑性中性轴夹角 ψ=0.599 9<β,最后由工况2的式 (31)计算得到管道在载荷1下的极限弯矩为4 628.6 kN·m。
4.2.2 文献[9]方法
用文献[9]中式(5)计算得到 σθd=505 MPa,用文献[9]中式(29)算得 k3=0.505、ψ=0.080 9<β。再由文献[9]工况2中的式(28)计算得到管道在载荷1下的极限弯矩为2 624.6 kN·m。
4.2.3 文献[15]方法
文献[15]中表1工况2的计算公式为:
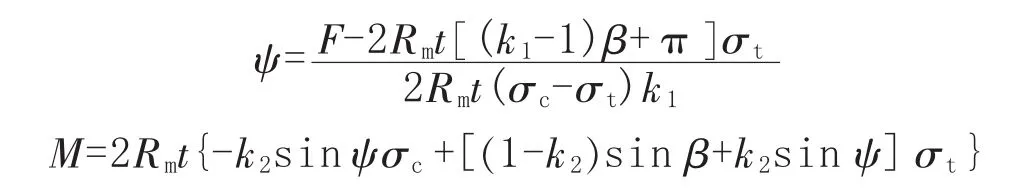
将 k1=0.505、k2=0.510、σc=-325.69 MPa、σt=575.69 MPa带入上述公式得到ψ=0.463 3<β,管道在载荷1下的极限弯矩为4 875.9 kN·m。
4.3 结果分析
同理,采用3种方法计算案例管道在载荷2、载荷3下的极限弯矩,结果见表2。

表2 3种方法计算的案例管道极限弯矩值
分析比较表2中的管道极限弯矩数值可知,①在p>0的每一种载荷下,文献[9]方法得到的计算值均最小,文献[15]方法得到的计算值均最大,本文方法得到的计算值居中。且文献[9]和文献[15]方法得到的极限弯矩计算值相差都很大。②对比文献[15]方法和本文方法计算的管道极限弯矩值,在载荷1下比较接近,而在载荷2、载荷3下相差很大。文献[9]方法计算的极限弯矩值比本文方法得到的计算值都小得多。③当p>0时,用文献[9]方法计算的管道极限弯矩值一般偏保守,甚至出现异常结果。用文献[15]方法计算的管道极限弯矩值可能很不安全。
5 结语
对在内压p、轴向力F和弯矩M联合作用下的局部减薄管道,存在极限弯矩的条件是,由内压p产生的环向应力σθd、σθ0和轴向力F同时满足式(19)。应用屈服准则和理想弹塑性本构模型,分4种工况建立了内压、轴向力和弯矩联合作用下局部等深减薄管道极限弯矩计算的新公式。笔者认为,文献[9-12]中定义的环向应力在管道未减薄区不一定满足屈服准则,文献[14-15]釆用的环向应力σθ=pRm/t在管道腐蚀区不一定满足屈服准则。因此,文献[9-15]中所推导的极限弯矩计算式的理论依据不充分。
