S型焊接金属波纹管外压失稳临界极限压力研究

陈赵勤，马咏梅，马传鑫，束 振，王 捷，王子涵，王泽平

（1.四川大学 机械工程学院，四川 成都 610065；2.四川日机密封件股份有限公司，四川成都 610045）

作为管道变形补偿元件［1］，焊接金属波纹管被广泛应用于石油、化工、电力等行业，起着密封、隔离介质及柔性连接等作用。焊接金属波纹管密封性能受其稳定性影响较大。

在GB 12777—2019《金属波纹管膨胀节通用技 术 条 件 》［2］、EJMA—1998 《Standards of the Expansion Joint Manufacturers Association》（第 7 版）［3］和 JIS B8277—1993《压力容器的膨胀节》［4］等国内外相关设计标准中，对承受外部介质压力的波纹管设计方法，均与承受内压工况的相似。Tsukimori K等［5］提出了 U型波纹管外压状态下失稳临界压力计算公式，张庆等［6］利用有限元法非线性屈曲分析研究了屈曲临界载荷，刘颖［7］对波纹管在弯矩载荷作用下进行了失稳分析，李志平等［8-9］采用极限载荷法研究了位移、波形相关参数以及波纹管各层之间的摩擦接触对波纹管稳定性的影响。

随着密封技术发展以及各行业的需求变化，对于焊接金属波纹管密封端面补偿性能要求越来越高，对其受外部介质压力状态时稳定性要求也进一步提高［10］。本文通过建立 S型焊接金属波纹管有限元模型，分析波纹管受外压状态下结构参数和工况参数对其稳定性的影响，确定结构失稳的临界载荷［11］，并提出了机械密封用焊接金属波纹管外压失稳临界极限压力拟合关系式。

1 焊接金属波纹管稳定性理论计算公式

1.1 周向稳定性

金属波纹管周向失稳表现形式为波纹管波峰塌陷或波谷外鼓［12］。EJMA—1998中提供了相应的U型周向稳定性校核方法，是将波纹管波纹视为1个与其具有相同横截面惯性矩的直圆筒，圆筒直径相当于波纹管平均直径，圆筒厚度则是惯性矩相等的波纹管的厚度［13］。按照该方法计算得出的外压圆筒周向失稳临界压力偏高，为波纹管临界压力的上限值。波纹管横截面惯性矩计算用图见图1。

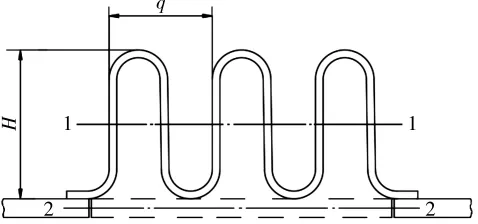
图1 波纹管横截面惯性矩计算用图

波纹管横截面对其形心轴的惯性矩计算公式如下：

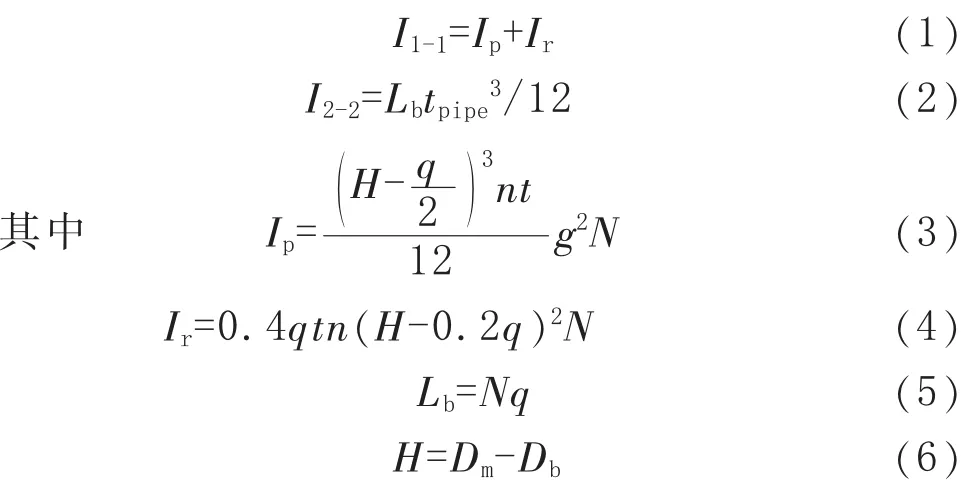
式（1）～式（6）中，I1-1为波纹管横截面对轴 1-1的惯性矩，I2-2为筒体部分对轴2-2的惯性矩，Ip为环板横截面的惯性矩，Ir为波纹管波峰与波谷2个半圆弧的横截面惯性矩，mm4；Lb为波纹管波纹段长度，H为波高，Dm为波纹管平均直径，Db为波纹管直边段和波纹的内径，q为波距，t为波纹管单层材料公称波厚，tpipe为等效圆筒的厚度，mm；n为层数；N为波数。

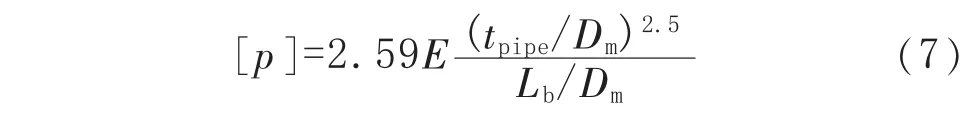
式中，E为弹性模量，MPa。

1.2 平面失稳临界压力

金属波纹管平面失稳表现形式为波纹平面的偏移或倾斜转动［14］，平面失稳是因介质压力引起的波纹管经向弯曲应力超出范围，应力达到了材料的屈服强度造成的。波纹管壳体壁面上沿着所在位置周向方向产生塑性铰线［15］，考虑金属波纹管的壁面处于平面应力状态，结合波纹管模型轴对称特点，塑性铰线位于波纹管波峰和波谷处，且该位置的应力等于1.5倍的材料屈服强度［16］。利用Mises屈服准则，其平面失稳机理计算公式如下：

式（8）～式（10）中，σs为波纹管材料在设计温度下的屈服强度，σm为经向应力，σc为周向应力，MPa；μ为泊松比；εm为经向应变，εc为周向应变。

在EJMA—1998中，失稳临界极限压力pcr为失稳极限设计压力psi的2.25倍［17］，即安全系数为2.25。对于两端固定长度和直径之比较小的无加强多波膨胀节，类比内压失稳原理，按照式（11）、式（12）求得单层金属波纹管外压失稳压力。按照该方法求解，忽略周向应力σc，按式（8）取σm≥1.5σs，所得的平面失稳极限设计压力psi为保守值。

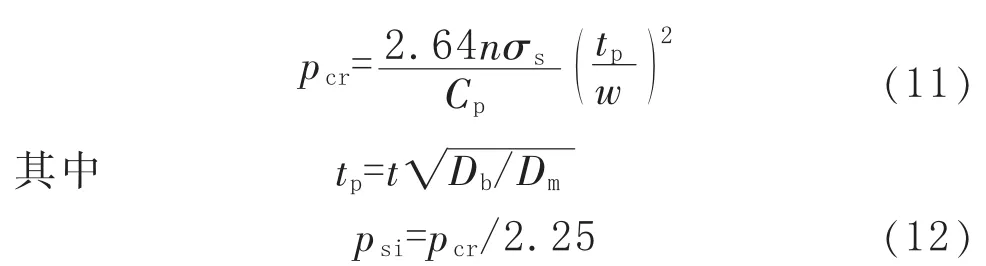
式（11）～式（12）中，Cp为与结构尺寸有关的修正系数；w为波高与波纹管材料厚度 nt之差，mm；tp为波纹管成形减薄后的单层壁厚，mm。

随壁厚的增加，由介质压力造成的周向薄膜应力σc增大，考虑周向薄膜应力对焊接金属波纹管平面失稳的影响，引入平面失稳影响系数α，从而确定的失稳极限设计压力psi为：

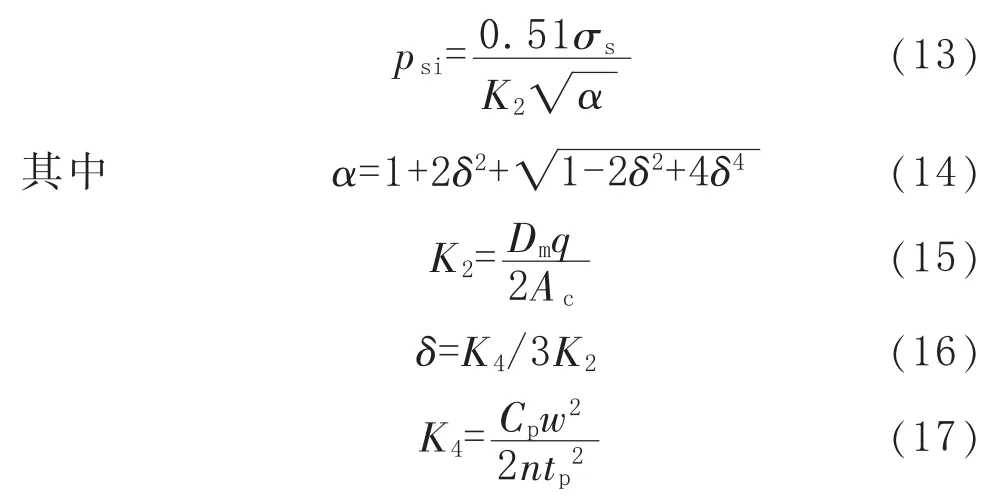
式（13）～式（17）中，K2、K4为平面失稳系数，δ为平面失稳应力比；Ac为单个波纹的金属截面积，mm2。

2 焊接金属波纹管稳定性校核计算

2.1 结构及参数

文中对S型60双层焊接金属波纹管进行研究。S型焊接金属波纹管波片由3段圆弧组成，波纹管及波片外形见图2。

图2 S型60双层焊接金属波纹管及波片外形

焊接金属波纹管材料为经过时效处理的Inconel-718，其密度为 8 240 kg/m3、弹性模量2×1011Pa、泊松比 0.3、屈服强度 σs=1 110 MPa。波纹管规格为60 mm，其波距q=1.47 mm、波厚t=0.152 mm、内径 Db=61.5 mm、波高 H=6.5 mm，波数 N=9，转速 3 600 r/min。

2.2 周向稳定性

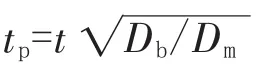
将焊接金属波纹管相应参数代入式 （1）～式（5），算得 Ip=87.37 mm4、Ir=61.96 mm4、 tpipe=5.14 mm、［p］=9.14 MPa。

2.3 平面失稳临界压力

不考虑平面失稳系数时，由σs=1 110 MPa、n=2、tp=0.144 6 mm、w=6.196 mm， 在 EJMA—1998中据波纹管结构参数查表得Cp=0.78。代入式（11）、式（12），计算得 pcr=4.098 MPa、psi=1.821 MPa。

考虑平面失稳系数时，由式（13）～式（17）计算得 psi=2.375 MPa，则有 pcr=5.35 MPa。

根据EJMA—1998计算所得结果可知，该型号焊接金属波纹管发生周向失稳之前已发生平面失稳。

3 焊接金属波纹管稳定性有限元仿真分析

3.1 模型建立及网格划分

采用建模软件建立S型60双层焊接金属波纹管三维模型，叠合波片之间间隙连接处设置为尖角的结构形式，得到的波纹管三维有限元模型见图3。

图3 S型60双层焊接金属波纹管三维有限元模型

工作时焊接金属波纹管最下层焊接在底座上，波纹管与介质油液相接触承受外压，最上层波片承受轴向压缩。根据工况确定边界条件，以波纹管体心为旋转中心添加工作转速，最下层波片外缘固定，最上层波片外缘加载y向位移约束，波片外侧加载2.5～4 MPa介质压力载荷。

选择自动扫掠划分方式对模型进行网格划分，细化波纹管波片外表面与介质压力接触处的网格单元尺寸，尺寸设置为0.24 mm，得到六面体网格单元，单元数为35 040，节点数为226 735。因波纹管结构形状及其施加载荷均具有轴对称性，故采用对称处理以提升工作效率。

采用线性屈曲分析模块，在其他参数不变时，在焊接金属波纹管模型上改变轴向压缩量、介质压力、扭矩、波纹管波数等参数数值，由有限元仿真结果分析金属波纹管外压失稳临界极限压力pcr的变化规律。

3.2 失稳临界极限压力影响因素

3.2.1 轴向压缩量与介质压力

根据实际工况，选取介质压力为2.5～4 MPa、轴向压缩量为4～6 mm，得到的轴向压缩量及介质压力对焊接金属波纹管失稳临界极限压力的影响曲线见图4。

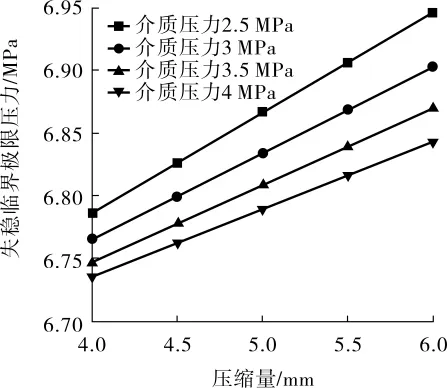
图4 轴向压缩量及介质压力对焊接金属波纹管失稳临界极限压力影响曲线

由图4可以看出，当介质压力不变时，失稳临界极限压力随轴向压缩量增大呈线性增大。介质压力越大，失稳临界极限压力受轴向压缩量影响越大。当其余工况和轴向压缩量不变时，失稳临界极限压力随着介质压力的增大而减小，即越容易发生失稳。

3.2.2 扭矩

不同扭矩下焊接金属波纹管失稳临界极限压力变化曲线见图5。

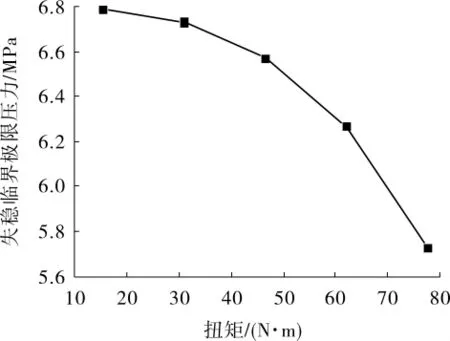
图5 不同扭矩下焊接金属波纹管失稳临界极限压力变化曲线

由图5可以看出，其他工况不变时，扭矩增大，失稳临界极限压力减小，且扭矩越大，失稳临界极限压力减小速率越大。

3.2.3 波数

考虑到波纹管机械密封件性能要求，波纹管结构参数中的波厚、波距和波形等参数已经固定，故对波数改变影响进行分析。选取介质压力为2.5 MPa、轴向压缩量为 4 mm、波数为 7～10，得到的不同波数下焊接金属波纹管失稳临界极限压力变化曲线见图6。

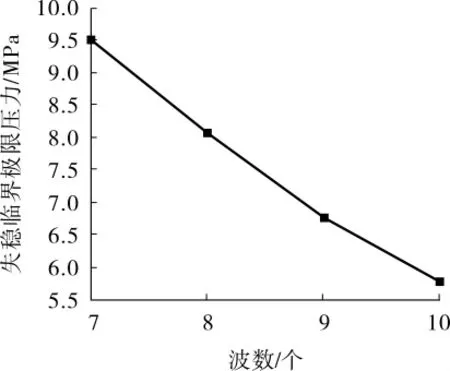
图6 不同波数下焊接金属波纹管失稳临界极限压力变化曲线

由图6可以看出，其他工况不变时，随着波数增大，焊接金属波纹管失稳临界极限压力减小。波数越大，波纹管越容易发生失稳。但波数过小，波纹管的弹性功能将无法满足预定工况要求，失去密封件的意义。

4 焊接金属波纹管稳定性仿真分析与理论计算结果对比

以介质压力为2.5 MPa、轴向压缩量为4 mm为例，以仿真结果为真值，定义相对误差Δ=［（仿真分析值-理论计算值）/仿真分析值］×100%，得到的焊接金属波纹管失稳临界极限压力理论计算与仿真分析结果对比见表1。

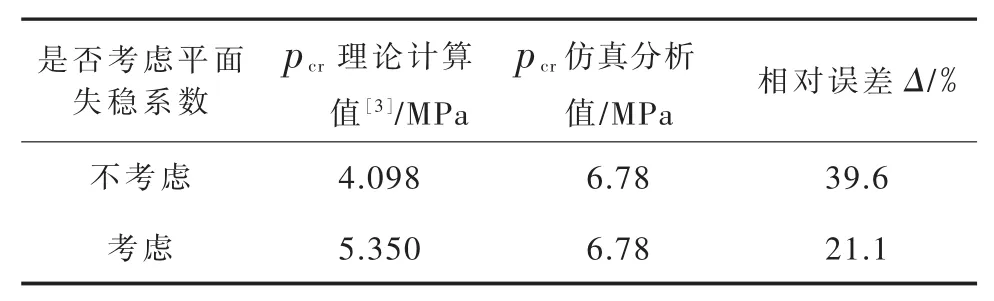
表1 焊接金属波纹管失稳临界极限压力理论计算和仿真分析结果对比

由表1可见，按 EJMA—1998得到的pcr理论计算值均小于仿真分析值，考虑到安全系数为2.25，且理论计算值为参考其他波形经验公式计算所得，故理论计算求解所得的平面失稳极限设计压力趋于保守。

从表1还可以看出，考虑平面失稳系数时，pcr理论计算值误差相对较小，在25%以内。后期研究可结合理论计算及仿真分析结果进行试验，得到S型焊接金属波纹管对应的安全系数值，再对理论计算式加以修正。

5 焊接金属波纹管失稳临界极限压力拟合关系式

设置初始方程为一次函数方程，设介质压力为p，轴向压缩量为x，对各介质压力下的pcr-x曲线进行一次函数方程拟合。再设斜率为Ks、常数项为Bs，分别拟合得介质压力p与Ks、Bs的关系式如下：

由于失稳临界极限压力与介质压力及轴向压缩量之间的基础形式均简化为线性关系，因此随机选取介质压力及轴向压缩量数值，即可由式（18）计算得到失稳临界极限压力。经对比，式（18）计算值与仿真值之间误差较小，均在1%以内，可为工程应用提供参考。

6 结语

根据EJMA—1998对S型60双层焊接金属波纹管稳定性进行周向稳定性理论计算校核，得出许用压力的上限。结合Mises屈服准则得出了焊接金属波纹管理论失稳临界极限压力。

通过有限元分析软件建立焊接金属波纹管分析模型，采用控制变量的方法研究了介质压力、轴向压缩量、扭矩和波数对波纹管屈曲失稳临界极限压力的影响。分析结果表明，随着介质压力的增大，失稳临界极限压力减小，波纹管越易发生失稳；随着轴向压缩量的增大，失稳临界极限压力呈线性增大趋势；随着扭矩的增大，失稳临界极限压力减小，所受扭矩越大，极限压力减小速率越快；随着波数的增多，波纹管越不容易发生失稳，在满足工况条件下可以选择合适的波数改善波纹管工作性能。

对于S型60双层焊接金属波纹管，采用EJMA—1998中外压失稳公式计算的结果与有限元仿真结果存在一定误差。在误差允许范围内，需结合试验取相应安全系数值对理论计算公式进行修正。拟合得到了该型号焊接金属波纹管失稳临界极限压力与介质压力、轴向压缩量的函数关系式，可为工程设计提供参考。