残缺互补判断矩阵次序一致性及排序方法
2021-07-16王国辉
吴 伟,王国辉,顾 丹
(1.辽宁工程技术大学 应用技术与经济管理学院,辽宁 阜新 123000;2.辽宁省技术创新研发工程中心 产业技术研究院,辽宁 沈阳110112)
0 引言
模糊层次分析法(FAHP)一直是学者们常用的一种有效的综合评价方法.作为模糊层次分析法的热点问题之一,由专家给出的两两比较的模糊互补判断矩阵的一致性及排序问题引起了大量学者的关注[1-3],并取得大量成果[4-11].但是在实际决策过程中,在进行方案两两比较时,决策者受专业结构、个人偏好等因素影响,会出现难以给出准确判断,或者不愿发表自己意见的情形,此时就会得到一个某些元素缺失的判断矩阵,即形成了残缺互补判断矩阵,因此对残缺互补矩阵的决策研究具有重要的现实意义[12].
近年来,残缺互补判断矩阵一致性及排序问题研究也得到了很多学者的关注,学者们分别基于加性一致性判断矩阵和乘性一致性判断矩阵给出相应一致性检验和排序方法.文献[3]对加性一致性残缺互补判断矩阵通过行和归一法来求解残缺互补判断矩阵的排序向量;文献[1]基于乘性一致性给出缺失元素的估计值和排序方法;文献[12]在分析了利用加性一致性的定义来估计残缺语言判断矩阵中的缺失元素的方法,并对其进行了改进,然后根据偏好值算术平均数对方案进行排序;文献[13]利用残缺互补判断矩阵的乘性一致性,给出了残缺互补判断矩阵权重向量最小平方法和权重向量最小偏差法两种排序方法;文献[14]分析了残缺互补判断矩阵的加性一致性定义,提出了最小方差法和二次规划法两种方法;文献[15]基于加性一致性残缺判断矩阵定义给出了转换公式,通过转换公式得到新的矩阵,之后通过目标函数方法获得排序向量;文献[16]基于加性一致性残缺区间数互补判断矩阵,通过建立数学规划模型求得排序向量.以上文献中学者们提出的方法都能对残缺互补判断矩阵进行一致性检验和排序,但是同时存在一些不足之处.首先,文献[3]、文献[13]~文献[16]缺失对残缺判断矩阵的一致性检验,如果残缺判断矩阵一致性程度不高,则利用该矩阵获得的排序结果不大可信;其次,文献[1]进行了一致性检验并对元素进行了调整,但对可接受的不一致临界值ε的确定没有给出依据,同时也易产生一致性悖论问题,另外需要调整的元素返回给专家,此做法在实际决策中也有待商榷;文献[12]对残缺判断矩阵进行了次序一致性性检验并排序,该检验和排序方法过程繁琐、不易操作,实际中很难掌握[17].
基于以上分析,本文给出残缺互补判断矩阵次序一致性检验、调整及排序的偏序集表示方法,对不满足次序一致性的残缺互补判断矩阵通过调整每个截集的传递性,使之达到完全次序一致性后,给出偏序关系矩阵,根据上集和下集特征,给出更为简捷的残缺互补判断矩阵排序方法.
1 基本概念
1.1 偏序集决策方法
定义1对于给定的集合C,R是C中元素的二元关系,若R满足
(1)自反性:对任意x∈C,有xRx;
(2)反对称性:对任意x,y∈C,若xRy且yRx,则x=y;
(3)传递性:对于任意x,y,z∈C,若xRy且yRz,则xRz.
则称R为C上的偏序关系,记作,偏序关系R和集合C合在一起我们记作(C,),称之为偏序集[18].
如果集合C中的元素有限,将偏序集用矩阵的形式表示出来,即偏序关系矩阵[24].
定义2给定偏序集(C,),对于∀ci,cj∈C,若cicj,则记sij= 1 ;若ci≻cj或者ci与cj不可比,则记sij= 0.则S=(sij)n×n为的偏序关系矩阵[18].
定理1设S=(sij)n×n为偏序关系矩阵,则G= (S−I)2,其中sij∈ ( 0,1),I为单位阵,G为布尔代数运算.
对于任意偏序关系矩阵S,称集合为x在C的下集;称集合为x在C的上集;称集合U(x)为x在C的不可比集,得到U(x) =C−O(x) −F(x).若以 及表示为O(x) 、F(x)以及U(x)元素个数,则对于m个方案的偏序集其x的O(x)、F(x)和U(x)元素个数满足
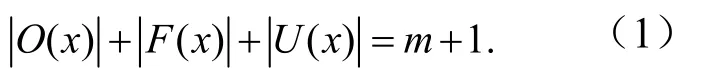
对于任意x∈A方案在偏序集上的高度为
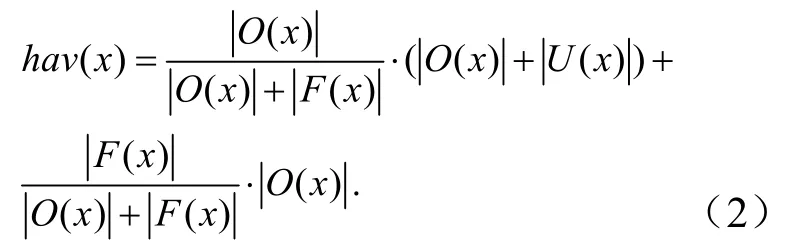
在偏序集决策方法中,最后各个方案通过计算在偏序关系矩阵中hav(x)大小进行排序[19].
1.2 残缺互补判断矩阵一致性
在多属性决策中,设X= {x1,x2, … ,xN}为方案集[20],且N= { 1 , 2,… ,n}.当方案较多时,决策者不容易给出方案的直接排序,但两两方案的优劣关系bij却容易给出,形成的矩阵为B= (bij)n×n,描述如下:
定义 3设矩阵B= (bij)n×n,若 ∀bij∈ [ 0,1],则称B是模糊矩阵[21].
根据定义3可知:
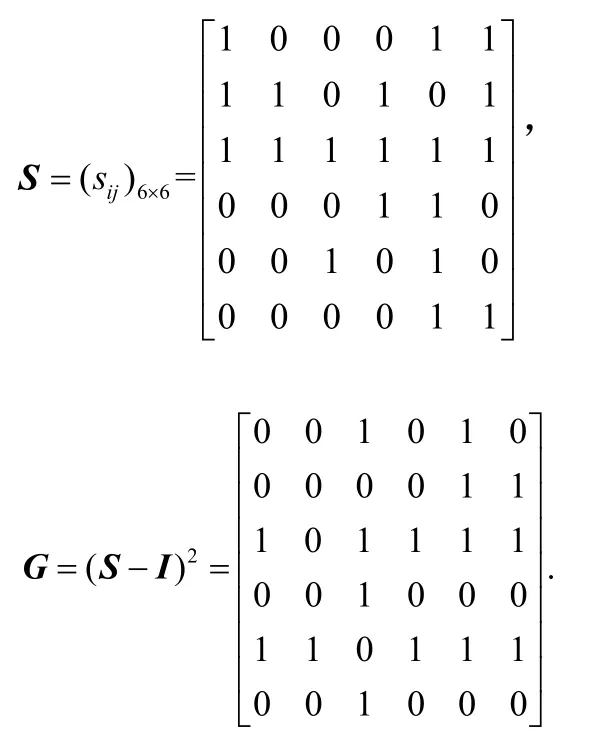
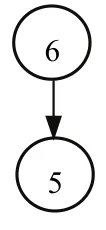
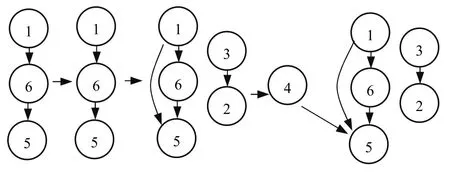
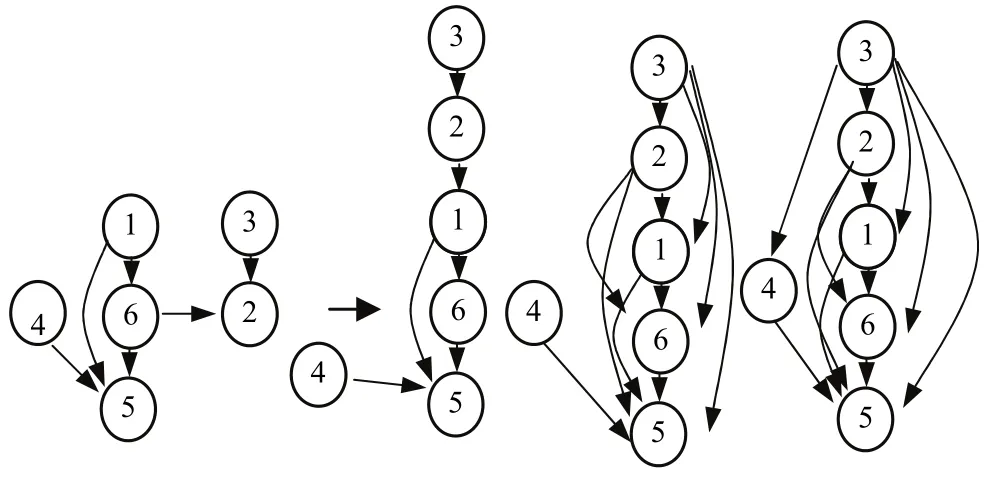
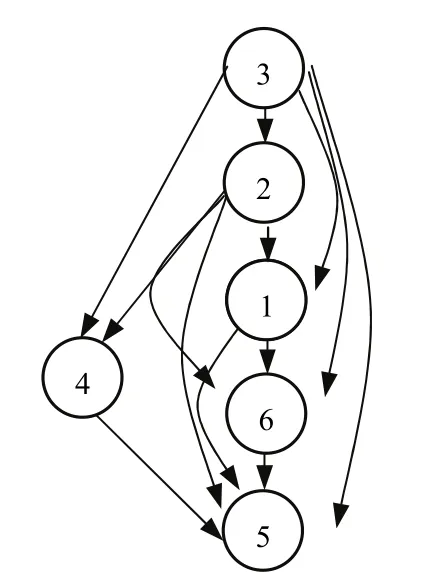
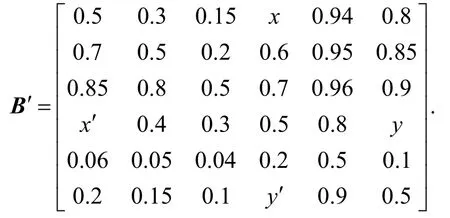
(1)0.5 (2)0 ≤bij<0.5,表示方案xj优于方案xi; (3)bij= 0.5,表示方案xi和方案xj同样重要. 定义 4若模糊矩阵B= (bij)n×n满足:对于∀i,j∈N有bij+bji= 1,则称B是互补判断矩阵[22]. 定义5如果互补判断矩阵B= (bij)n×n中既含残缺元素又含非残缺元素,且非残缺元素满足bij+bji=1,bii=0.5,bij≥ 0 ,则称B为残缺互补判断矩阵[1]. 定义6对于残缺互补判断矩阵B= (bij)n×n,若∀i,j,k,bij≥ 0.5,bjk≥ 0.5时有bik≥ 0.5,则称B具有次序一致性[23]. 定义6给出了判断任意残缺互补判断矩阵是否满足次序一致性的标准,对于方案较少时,很容易判断,当比较的方案较多时,判断起来就会很困难.另外,该定义重点关注的是方案之间的优劣关系,为得到更加准确的排序向量,还需要关注方案之间的比较的重要程度,因此考虑按照定义7将残缺互补判断矩阵进行如下转换. 定义7设残缺互补判断矩阵B= (bij)n×n对任意λ∈ [ 0 , 1],称Bλ=(rij)n×n为B的截集矩阵,其中 定义8对于残缺互补判断矩阵B,如果任意方案xi>xj,都有bik>bjk(k= 1 ,2,… ,n),称B具有完全次序一致性[24]. 定理1给定偏序集(C,≺),若G中对于任意元素gij= 1 (i≠j,k= 1 ,2,…,n)时,都有sij= 1 (i≠j),则残缺互补矩阵B满足次序一致性. 证明 ⇒ 若gij=sik×skj=1(i≠j,k= 1 ,2,… ,n), 则sik= 1 且skj= 1 ,即xi>xn且xn>xj,又因为sij= 1 ,即xi>xj,满足定义6,因此,残缺互补矩阵B满足次序一致性. ⇐若残缺互补矩阵B满足次序一致性,则根据定义 6,当bik>0.5,bkj> 0.5时,bij> 0.5,即根据定义2所得当rik=1,rkj= 1 时,rij= 1 ,满足gij=sik×skj= 1 (i≠j,k= 1 ,2,… ,n)时 , 都 有sij= 1 ,证毕. 上述定理1给出了判断任意残缺互补判断矩阵是否满足次序一致性的方法,将残缺互补判断矩阵表示成为偏序关系矩阵后,按照公式G= (S−I)2进行布尔代数运算,如果在矩阵G中gij(i≠j)= 1的元素,在S中对应位置的元素sij(i≠j) = 1 ,则残缺互补矩阵B具有次序一致性,反之,残缺互补矩阵B不具有次序一致性. 定理2给定偏序集,残缺互补矩阵B具有完全次序一致性 ⇔Bλ( 0.5 ≤λ≤ 1) 满足传递性. 证明 ⇒对于任意Bλ,如果xi>xj,bij> 0.5,假设xj>xk,bjk> 0.5时,因为残缺互补矩阵B满足定义8,具有完全次序一致性,所以,xi优于xj时,bik>bjk,所以bik>bjk> 0.5,再由定义3中(1)可得,xi>xk,即xi>xj,xj>xk⇒xi>xk,满足定义1中的(3); ⇐如果Bλ( 0.5 ≤λ≤ 1) 满足定义1中的(3),根据传递性可得,当xi>xj,如果xj>xk时,xi>xk,又根据模糊矩阵定义 3可得,xj>xk、xi>xk方案j优于方案k,方案i优于方案k可表示为bik和bjk,因为任意Bλ( 0.5 ≤λ≤ 1) 中的元素都满足传递性,这就意味着当xj>xk存在于Bλ( 0.5 ≤λ≤ 1) 中时,即bjk≥λ,xi>xk必须存在截集矩阵Bλ1( 0.5 ≤λ<λ1≤ 1)中,即bik≥λ1,又因为λ1>bjk≥λ,所以bik>bjk,证毕. 定理 2给出调整残缺互补判断矩阵满足完全次序一致性的方法,该方法就是通过调整残缺互补判断矩阵的任意截集都使其满足传递性,因此,如果通过定义1的检验方法判定残缺互补判断矩阵不满足次序一致性,那么就可以通过定理2进行调整即可. 定理3设S=(sij)m×n为偏序集的偏序关系矩阵,对于 ∀ci,cj∈C,若Τ(ci)≥Τ(cj),则hav(ci)≥hav(cj), 其 中 证明 式(2)可以简化为 O(ci)又因为Γ(ci) =, 所 以Τ(ci) ≥Τ(cj) ⇒hav(ci) ≥hav(cj),证毕.所以,根据定理 3可以根据偏序关系矩阵中每个方案的下集O(cj)(行和)和上集F(cj)(列和)的比值大小进行排序. 因此,残缺互补判断矩阵次序一致性及排序的偏序集表示方法步骤如下: 步骤1根据定义2给出残缺互补判断矩阵的偏序关系矩阵S(残缺元素暂时认为不可比,数值为0),根据定理1对S进行判定,若满足次序一致性则转到步骤3,否则转到步骤2; 步骤2根据定理2逐个调节S的截集矩阵满足传递性,得到调整后的残缺互补判断矩阵B′,返回到步骤1; 步骤3根据调整后的残缺模糊互补判断矩阵,给出偏序关系矩阵,根据定理3求出方案的排序. 某投资公司欲就建立一个购物中心进行可行性研究,设有6个地点X={x1,x2,x3,x4,x5,x6}可供选择,设某专家给出残缺互补判断矩阵B= (bij)n×n如下,试确定最佳地点. 步骤1根据定义2给出残缺互补判断矩阵的偏序关系矩阵S并求出G. 根据定理1,在G中 而在S中对应位置 则矩阵B不具有次序一致性,转到第二步. 步骤2把矩阵B中的大于等于0.5的元素从大到小排列为0.9 > 0.8 > 0.7 > 0.6 > 0.5. B0.9关系图见图1,满足传递性. 图1 截集矩阵B0.9关系Fig.1 cut set matrix B0.9 relation B0.8关系图调整过程见图2,首先增加的是1→6,根据传递性,增加1→5,根据定理 2,B中b15修改为0.94,然后增加的是3→2和4→5,根据定理2,不需要调整. 图2 截集矩阵B0.8关系调整过程Fig.2 cut set matrix B0.8 relation adjustment process B0.7关系调整过程见图3.首先,新增加的关系是1→5,这个关系在B0.8关系图中已经出现;其次是2→1,依据传递性,需要增加的线为2 → 6 ,2 → 5 ,3 → 1 ,3 → 6 ,3 → 5,根据定理 2,B中b25,b35分别调整为0.95,0.96;b26,b36分别调整为 0.85,0.9;b31调整为 0.85.再次,是2→6已经出现,最后是3→4,无需调整. 图3 截集矩阵B0.7关系调整过程Fig.3 cut set matrix B0.7 relation diagram adjustment process B0.6关系图调整过程见图4:新增加的关系是2→4,不需要调整,其次增加的是3 → 1 ,3 → 6,在B0.7关系图调整过程已经出现,此时,任意截集都满足传递性. 图4 截集矩阵B0.6关系调整过程Fig.4 cut set matrix B0.6 relation diagram adjustment process 所以,调整后的残缺互补判断矩阵为 返回到步骤1,根据定义2给出残缺互补判断矩阵B′的偏序关系矩阵S,根据定理1判断满足次序一致性(过程略),因此转到步骤3. 步骤3根据定理3,hav(xi) 大小跟xi行和与列和的比值成正比,所以从上面的偏序关系矩阵S′计算得 从表1可见,本文排序结果和文献[25]排序结果完全一致,和文献[1]的排序略有不同,原因在于调整方法的角度不一样所致,但两种方法都能选出最优方案x3. 表1 不同文献排序结果对照Tab.1 comparison of ranking results of different literatures 本文提出的残缺互补判断矩阵的一致性检验、调整及排序方法与其他文献的同类方法相比有两点优势:① 残缺互补判断矩阵具有较高的一致性.本文在对方案排序前,对残缺互补判断矩阵进行了次序一致性改进,并且赋值有依据,不仅解决了文献[25]中由于没有进行一致性检验所带来的结果可靠性问题,同时也规避了文献[1]检验残缺互补判断矩阵一致性存在的悖论问题[26].② 排序方法简捷.文献[1]、文献[25]通过计算残缺元素的估计值进行排序,根据不同的估计值的计算较繁琐,而本文的排序方法无需估计残缺元素的具体值亦能进行有效排序,简单易操作.③ 本文排序方法具有良好的鲁棒性.对于排序方法鲁棒性的分析是验证该方法可靠性的不可缺少的环节. 本文排序方法的鲁棒性体现在以下方面:① 对于残缺互补判断矩阵中残缺元素应用不同的估值方法,导致方案的排序结果不同,如文献[1]和文献[25],容易造成决策者困惑,对于本文提出的残缺互补判断矩阵排序方法,使得残缺互补判断矩阵中已知元素满足次序一致性基础上,无需计算残缺互补判断矩阵中的估计值亦能对方案进行排序,且结果唯一;② 本文的排序结果中方案3和方案2是最优和次优,方案5最差,和文献[1]和文献[25]中同类方案排序结果完全一致,能够选出最优和最劣方案. 针对现有残缺互补判断矩阵一致性检验、调整和排序方法中存在残缺矩阵一致性程度不高、赋值缺乏依据、估计残缺元素及排序运算过程繁杂问题,给出了残缺互补判断矩阵次序一致性及排序的偏序集表示方法,并得出了以下结论. (1)利用偏序集中偏序关系矩阵的转换关系给出了残缺互补判断矩阵次序一致性的检验定理. (2)针对不满足次序一致性的残缺互补判断矩阵给出了调整定理. (3)对于满足次序一致性的残缺互补判断矩阵,在不估计残缺值的情况下给出排序方法,该方法也是本文研究的一个特色体现. (4)通过和传统的残缺互补判断矩阵次序一致性的检验、调整、排序方法比较发现,本文的检验和调整方法赋值有依据、易操作,其他文献都是在估算估计值后提出的排序方法,其结果不稳定,而本文提出的排序方法鲁棒性强.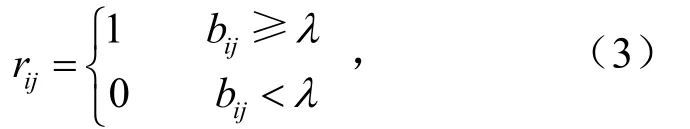
1.3 残缺互补判断矩阵一致性及排序偏序集表示

2 算例

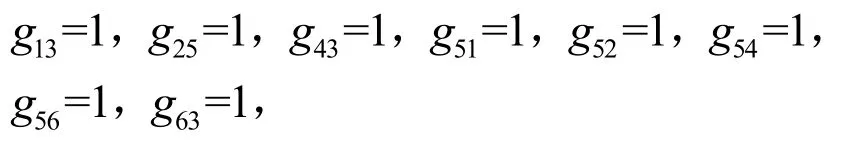
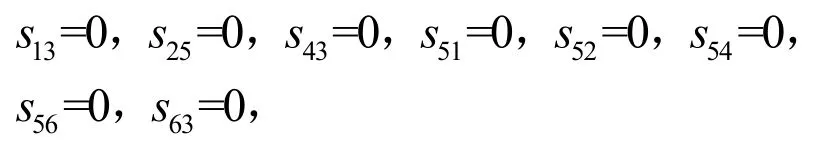
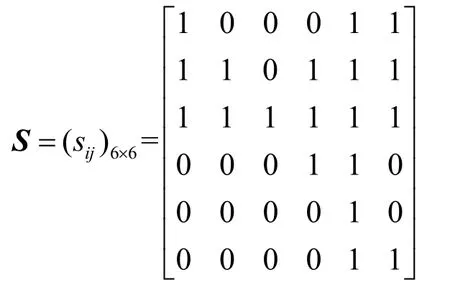
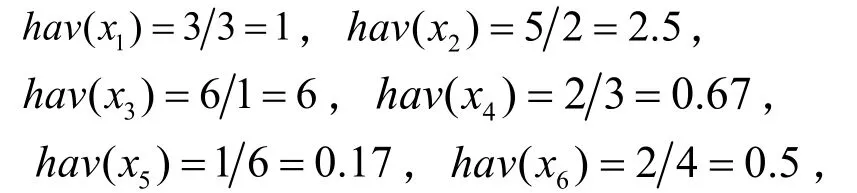

3 结论
