高增益开关电感磁集成组合Boost-Zeta变换器
2021-07-16荣德生孙瑄瑨
荣德生,张 熙 ,孙瑄瑨
(辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105)
0 引言
近年来,全球化石能源告竭的问题逐渐突出,新能源如太阳能、风能等,由于其清洁而且可再生的优点而备受关注.在新能源发电技术中,各种分布式电源的输出端与大电网并网的技术成了关键技术之一,为满足后级的并网逆变以及直流输电等高电压等级的需求,需要一种升压能力高的 DC-DC变换器.于是高增益的DC-DC变换器成了学者们的研究热点[1-6].
对于高增益 DC-DC变换器来说,提升电压增益的方式主要有级联倍压技术、倍压结构倍压技术、组合倍压技术等.文献[7]将有源开关电感结构与开关管-二极管结构级联,分别调节两级的占空比从而实现高电压增益的目的.文献[8]将 2个半桥单元通过中间电容级联,通过4个开关管交错导通来实现变换器的电压增益提升.对于文献[7]和文献[8]来说,虽大大提升了变换器的电压增益,但是由于结构中开关器件过多,变换器的控制方式较为复杂,且存在位于输出端的开关管电压应力过大的问题.文献[9]通过将开关电容单元与电感倍压结构进行级联,从而提高电压增益,且有效地减小了开关管应力太大的问题.对于这种采用级联方式的变换器来说,虽然变换器增益大大提升,但是其控制方式较为复杂,文献[10]提出将Cuk变换器组合叠加开关电容结构,每叠加一个开关电容结构,变换器的电压增益将成倍提升,开关管应力也将不断减小.文献[11]将Boost变换器与Buck-Boost变换器进行叠加组合,提升了变换器的电压增益.但上述几种变换器仅考虑通过改变变换器的拓扑结构来提升变换器的电压增益,缺少内部磁性元器件集成的研究,会出现较大的电流纹波.故文献[12]提出组合式Sepic变换器,将拓扑中的两个电感器进行磁集成,不仅提高变换器的电压增益,而且减小了电感电流纹波.文献[13]提出组合式Cuk变换器,通过磁集成的方式集成了变换器中的3个电感器,使得所有电感电流纹波均减小.但对于文献[12]、文献[13]来说,单独的Sepic/Cuk进行叠加组合,倍压能力提升得并不高,且过多的叠加组合会造成磁集成困难以及变换器的器件过多,对变换器性能造成一定的影响.文献[14]研究了一种带有磁集成的Zeta变换器,通过将两个倍压单元级联提升了电压增益,通过磁集成减小了变换器的电感电流纹波.
本文引入拓扑组合的思想,将Boost变换器与Zeta变换器进行组合,得到组合Boost-Zeta变换器.然后引入“LCL”型开关电感结构,对三个电感器进行磁集成,同时调整变换器的后级结构,提出高增益开关电感磁集成组合 Boost-Zeta变换器.该变换器具有较高的电压增益,同时保留Zeta变换器输出电流连续的特点,通过磁集成设计,给出合理的集成方案,使三电感电流纹波均减小,通过实验证明该变换器具有较好的性能.
1 新型变换器拓扑结构
根据 Boost变换器和 Zeta变换器工作方式可知,其输入端均具有一个开关管-电感器结构,输入端电感在开关管导通模态下均为单独储能,而在开关管关断模态下均向后级释放能量.为了提升变换器电压增益的同时,保留两种变换器各自的特性,将等效Boost变换器结构当作基底,向上层叠Zeta变换器的电容器-二极管-电感器(C-D-L)结构,在输入端共用同一开关管-电感器前级结构,将等效Boost变换器与Zeta变换器的输出端串联,得到了组合Boost-Zeta变换器,在节省器件的同时,提升变换器的电压增益.
“LCL”型开关电感由2个电感器、2个二极管和1个电容器组成,其工作实质为:电感器和电容器并联储能,串联放电,通过替换变换器中的储能电感,以达到提升变换器电压增益的效果.为了进一步提高组合Boost-Zeta变换器的电压增益,在上述组合变换器的基础上,引入 “LCL”型开关电感结构,同时调整了变换器的后级结构,再将L3作为输出电感,同时将变换器中的3个电感器通过磁集成技术进行集成,得到具有开关电感的磁集成高增益组合Boost-Zeta变换器,其拓扑演化过程见图1.

图1 开关电感磁集成组合Boost-Zeta变换器拓扑推衍Fig.1 deduction of magnetically integrated switching inductors combination boost-zeta converter
2 工作过程
做以下假设以便于原理分析:所有二极管、开关管为理想器件;电感器、电容器均为理想器件;所有电容器容量足够大,纹波电压可忽略.
假设三个电感器均工作在连续工作模式(Continuous Conduction Mode,CCM),令电感器L1=L2=L,电感器L3=L′;L1与L2的互感为M1,电感L1、L2与L3的互感为M2.
一个开关周期内,变换器有3个模态.图2为各模态等效电路,其主要波形见图3.

图2 开关电感磁集成组合Boost-Zeta变换器工作模态Fig.2 operating modes of magnetically integrated switching inductors combination boost-zeta converter

图3 开关电感磁集成组合Boost-Zeta变换器主要波形Fig.3 main wave forms of magnetically integrated switching inductors combination boost-zeta converter
模态I[t0~t1]:开关管S导通,二极管D1、D2导通,D3、D4反向截止,输入电源Vin分别通过D1、D2为电感器L1、L2充电,iL1、iL2线性上升,同时Vin通过D1、D2为电容器C1充电;输入电源Vin、电容器C3、C2通过开关管S串联为电感器L3储能同时给负载供电,iL3线性上升.模态I回路电压方程为

模态II[t1~t2]:开关管S关断,二极管D4导通,D1、D2、D3截止,电感器L1、L2电容器C1通过D4为电容器C2充电,iL1、iL2线性下降;电容器C3串联电感器L3通过D4给电容器C4充电,iL3线性下降.模态II各回路电压方程为
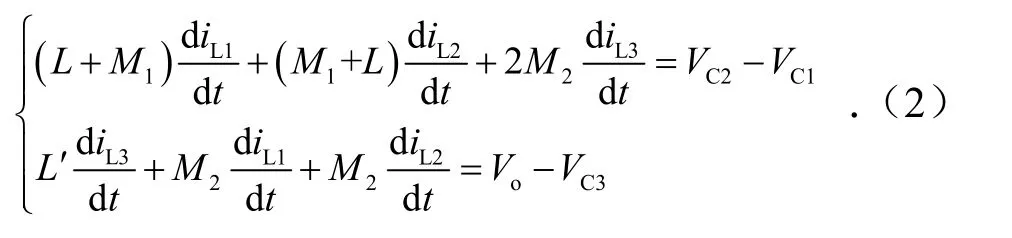
模态 III[t2~t3]:开关管 S关断,二极管D3、D4导通,D1、D2截止,电感器L1、L2电容器C1串联通过二极管D4给电容器C2充电,同时Vin、电感器L1、L2及电容C1通过D3给电容器C3储能,iL1、iL2线性下降;电感器L3通过D4给电容器C4储能,iL3线性下降.工作模态III各回路电压方程为

3 变换器性能
3.1 变换器静态特性分析
当变换器工作在CCM下,由式(1)和式(3)得电感器在上升和下降阶段电流变化量为

根据电感伏秒平衡原理,在一个周期内电流的上升量等于下降量,由式(4)和式(5),可得
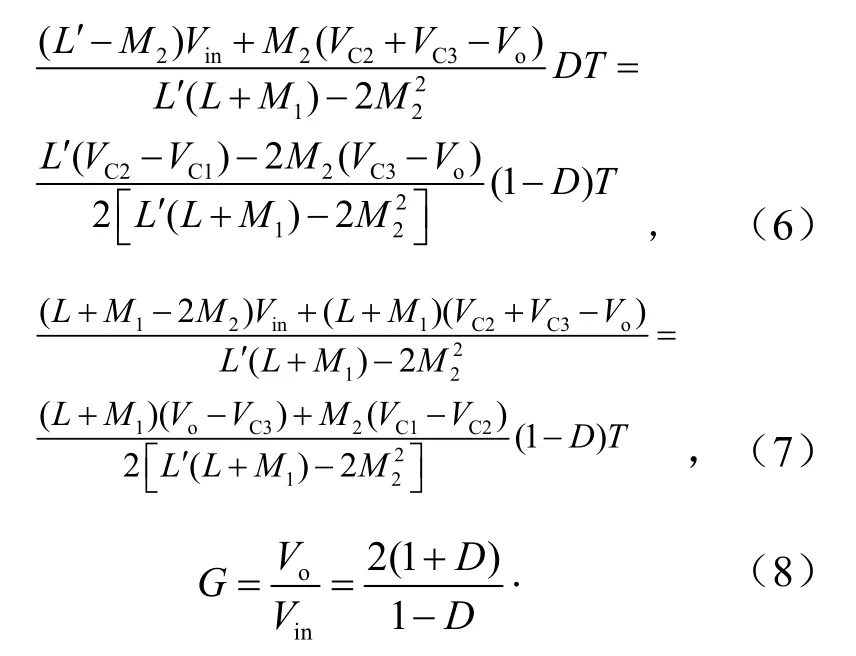
由式(8)可知,高增益组合 Boost-Zeta变换器电压增益G为组合Boost-Zeta变换器电压增益的2倍,说明通过替换LCL开关电感单元,变换器电压增益成倍提升,使变换器具有更宽电压调节范围,避免了变换器工作在极限占空比情况.
变换器在CCM下各器件的性能参数为
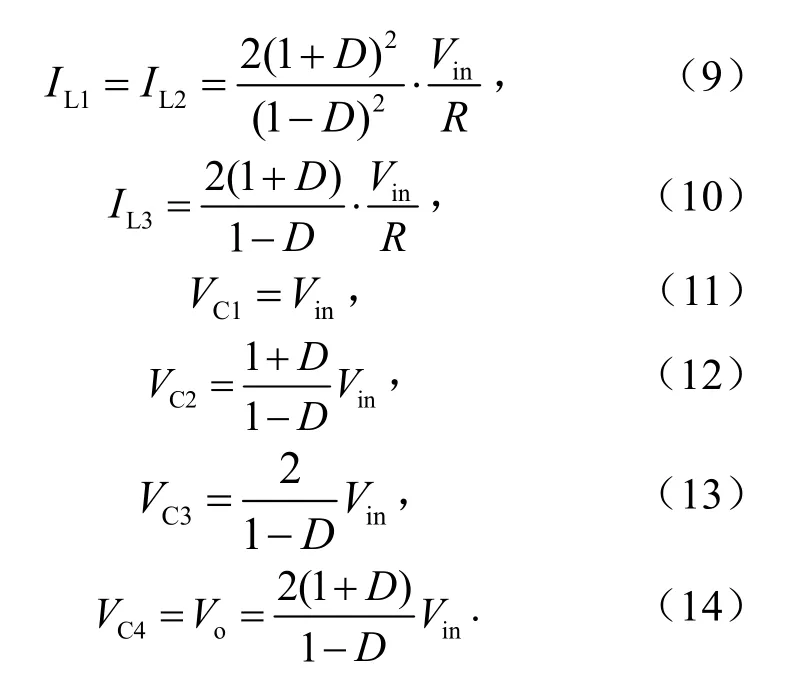
在电路中电容相当于恒定电压源的作用,其电压纹波过大会对变换器的性能造成严重的影响.假设电容电压纹波系数为Δv,f为开关频率,电容值[15]为

一般情况下,电容电压纹波应设计为电容电压大小的1%,即Δv=1%.
开关管电压应力为
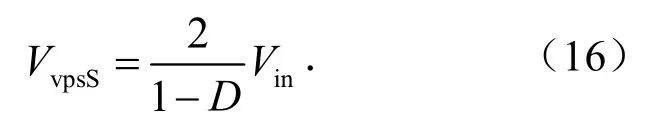
各二极管电压应力为

3.2 电流纹波分析
由式(4)、式(5)可知,电感器L1、L2、L3的电流纹波ΔiL1、ΔiL2、ΔiL3的大小既和自感有关,同时还与互感M1、M2有关.
假设L1与L2的耦合系数为电L1、L2与L3的耦合系数为电感L1(2)与L3的比值为λ=L1(2)L3,则根据式(4),在电感电流上升阶段,有
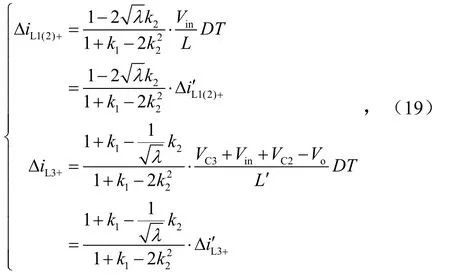
令
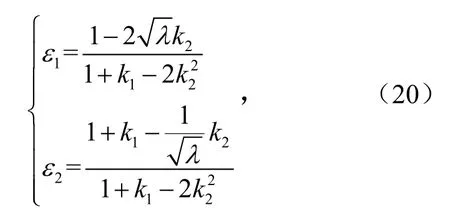
式中,称ε1、ε2为电感器L1、L2和电感器L3的电流纹波的减小系数.
为减小电感电流纹波,只考虑电感电流纹波减小系数ε<1的情况.电感L1、L2为LCL开关电感结构,二者工作方式相同,所以在集成设计中,电感器L1、L2可全耦合[13,16].故为考虑集成磁件设计,令k1=1,纹波减小系数ε与电感耦合系数k2在不同λ下的关系见图4.


图4 不同 λ下 ε1、ε2与 k2的关系Fig.4 relationship between ε1, ε2 and k2 under different λ
由图4中可以看出,当λ不同的情况下,ε1、ε2的变化趋势也不相同.当λ不断增大时,ε1不断减小,且减小的趋势不断增加;而ε2虽然减小但其减小的趋势越来越小.反之,当λ不断减小时,ε1减小的趋势逐渐减小,ε2减小的趋势逐渐增加.由于电感器L3位于输出端,其电流波动对后级具有一定的影响,故在实际设计中应令λ<1,选择ε1、ε2这2个纹波系数均减小的情况,再通过调节耦合系数k1,进而调节3个电感器的电流纹波.
3.3 性能对比
将本文提出的变换器与传统的Boost变换器、文献[14]提出的磁集成高增益Zeta变换器以及文献[10]提出的组合式Cuk变换器进行参数对比,具体对比见表1.

表1 性能对比Tab.1 performance comparison
图5为4种变换器电压增益对比,在上述4种变换器中,本文所提的具有开关电感的磁集成高增益Boost-Zeta变换器具有最高的电压增益,且电压调节范围最宽.

图5 变换器电压增益对比Fig.5 converter voltage gain comparison
图6为开关管电压应力对比,由图6可知,该变换器在高电压输出的情况下开关管电压应力均小于输出电压.

图6 变换器开关管电压应力对比Fig.6 converter voltage and voltage stress comparison
为验证变换器原理分析的正确性以及相同参数情况下与文献[10]以及文献[14]的对比,利用PSIM仿真软件,对3种变换器进行仿真验证.
首先,取相同输入电压Vin=12 V和占空比D=0.6的情况,3种变换器的输出电压的仿真波形见图7.由图7可以看出,在相同输入电压和占空比的情况下,本文所提变换器的输出电压最高,约为96 V,与理论分析完全相符,相较于文献[10]和文献[14],在电压增益上具有优势.

图7 3种变换器输出电压波形对比Fig.7 three converter output voltage simulation waveforms
然后,对比3种变换器在相同输入输出情况下(Vin=12 V,Vo=96 V),调节占空比得到变换器的主开关管电压应力仿真,波形见图8.由图8可知,3种变换器的主开关管电压应力均低于输出电压,对比3种变换器的电压应力,本文所提虽略大于文献[10],但此情况下其占空比却远远小于其他两种变换器,体现出高增益、低应力的性能优势.
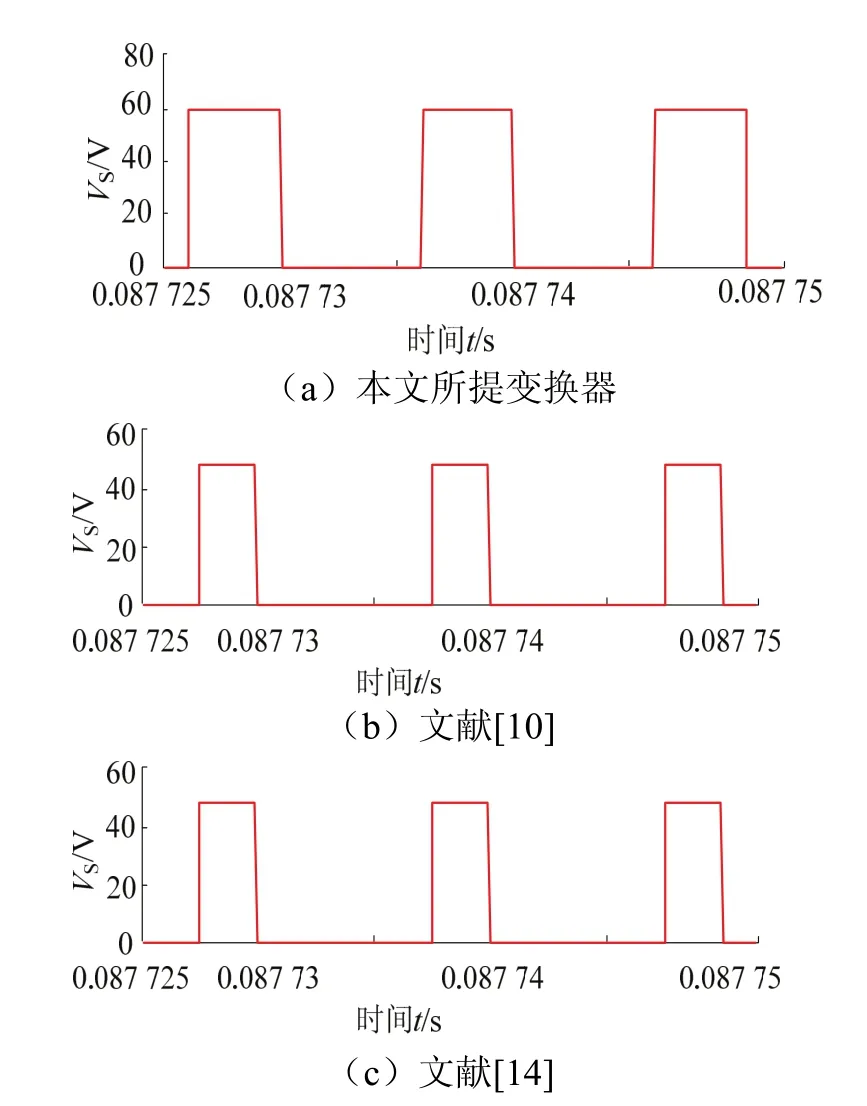
图8 3种变换器电压应力仿真波形Fig.8 three converter voltage stress simulation waveforms
4 变换器的磁件设计
电感器L1和L2为正向全耦合;L3和L1、L2正向耦合,其耦合系数需调节.在进行电感集成设计中,为方便调节电感单元间的耦合系数,可采用“EE”型磁芯来进行设计.
磁件结构和缠绕方式见图9.
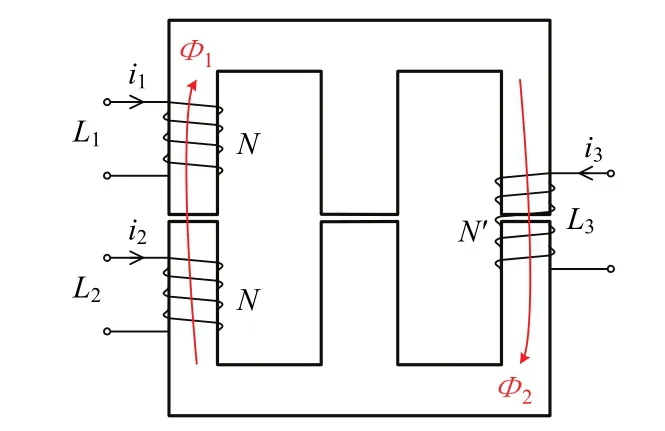
图9 三电感耦合磁件设计Fig.9 design of four inductively coupled magnets
根据磁芯结构,得到磁芯的磁路模型见图10(a),其中ℜ11、ℜ12、ℜ22为磁路磁阻,ℜg1、ℜg2为气隙磁阻;电感器L1、L2的匝数为N,L3的匝数为N′.通过对磁路模型进行磁阻合并,利用对偶变换以及尺度变换,得到磁芯结构的等效电路模型见图10(b),其中


图10 3电感集成的“EE”型磁件模型Fig.10 three inductance integrated "EE" type magnetic parts model
由图10(b),根据电感和磁阻之间的关系,得到电感L1、L2、L3的自感与磁阻的关系为

电感器L1、L2、L3之间的互感M与相应磁阻的关系为
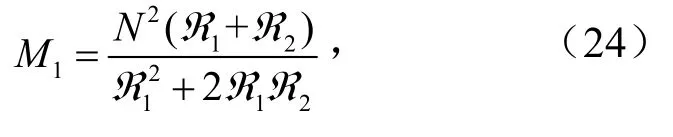

式中,M1为L1与L2的互感系数;M2为L1、L2与L3的互感系数,则耦合系数k1、k2分别为

根据以上分析,电感器L1与L2为全耦合,通过调节耦合系数k2,可以设计出符合设计要求的磁件.在实际应用中,根据式(27)调节中柱气隙大小进而可以调节耦合系数k2,再设计合理的匝数比,即可满足设计要求.
5 实验分析
制作一台功率为100 W的实验样机,参数如下:输入电压Vin=12 V,输出电压Vo=96 V,开关频率f=100 kHz,占空比D=0.6,电感L1=L2=20 μH,L3=80 μH,电容C1=C2=47 μF,C3=C4=100 μF.开关管选用 IRF540N,二极管型号为肖特基二极管MBR20100.变换器采用单电压闭环控制方式,输出电压用 LV-25P霍尔传感器进行采样,以TMS320F28335作为主控,采用增量式PI控制方式,通过 EPWM 调制模块产生 PWM 经过驱动光耦HCPL-3120驱动开关管,保证变换器的输出电压稳定,变换器的控制框图见图11.

图11 变换器控制框图Fig.11 converter control block diagram
由于L1(2)与L3的比值λ为0.25,根据图4(b)可知,当耦合系数k2趋近于1时,三电感器的电流纹波均减小.故在实验中,对于k2来说,可取k2=0.9,而电感器L1、L2由于参数相同,且为全耦合,故采用双线并绕的方式来提高耦合度.实验中,独立电感器使用环形铁硅铝 KS106125A磁芯,磁件磁芯选择EE32型磁芯,采用ETA5301A电流探测钳来进行电流测量,单位为100 MV/A.测量所得独立电感器和集成电感参数见表2.

表2 独立电感器和集成电感参数Tab.2 independent and integrated inductance parameters
变换器输出电压波形见图12,变换器电感器电流波形见图13、图14,开关管电压波形见图15.
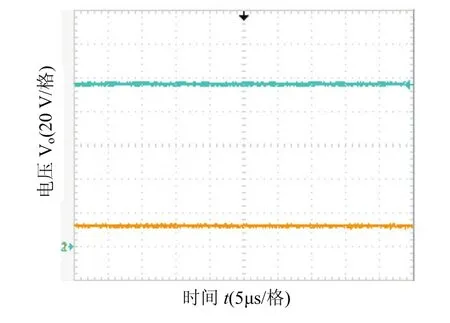
图12 Vin和Vo的实验波形Fig.12 experimental waveforms of Vin and Vo

图13 电感器L1(2)电流波形Fig.13 inductor current waveform of L1(2)

图14 电感器L3电流波形Fig.14 inductor current waveform of L3

图15 开关管电压波形Fig.15 voltage waveform of the switch tube
由图12可知,当输入电压为12 V时,输出电压约为96 V,与理论相符.由图13、图14可知,磁集成后,电感器L1和L2电流纹波由3.5A下降至1 A;电感器L3电流纹波由1.6 A下降至0.7A,由于漏感的存在,误差在可接受范围内.由图15可知,开关管的电压应力约为60 V,理论与实际相符合.
6 结论
(1)将Boost变换器与Zeta变换器进行组合,将“LCL”开关电感单元与磁集成技术应用于其中,提出了开关电感磁集成组合Boost-Zeta变换器.
(2)分析变换器的工作原理并根据变换器的工作特性,设计了集成磁件结构,通过实验验证了理论的正确性.本文所提变换器具有以下特点:Boost变换器与Zeta变换器进行组合,同时共用同一开关管-电感器前级结构,可在节省器件的同时,提升变换器的电压增益,减小了开关管的电压应力.将“LCL”开关电感单元引入拓扑结构,变换器的电压增益进一步提升.
(3)通过对拓扑中的3个电感器进行磁集成,同时对集成磁件进行设计,减小了电感电流纹波,优化了变换器的性能.
