熵值法与GWO-SVM耦合模型在滑坡预警中的应用

田文财,李 青

(中国计量大学 机电工程学院,浙江 杭州 310018)

我国地形地貌复杂,各地环境差异较大,每年发生的自然灾害较多,类型较为复杂。在各种自然灾害中,滑坡所占比例较大,造成的经济损失较多。以2020年为例,全年气候较差,降雨较多,共造成1.38亿人次受灾,直接经济损失高达3 701.5亿元,其中洪涝、滑坡造成的损失占多数。为减少滑坡等自然灾害造成的损失,各国学者以数学理论为基础,提出了多种预警方法,并按照边坡的位移与稳定性将预警方法分为:确定性预报模型、统计预报模型和非线性预报模型[1]。确定型预报模型如斋藤迪孝法,将滑坡分为三个阶段,通过建立加速蠕变方程预测理论上的滑坡发生时间,并于1970年成功预测了日本高场山滑坡[2]。统计预报模型代表方法为GM(1,1)灰色预警模型,它通过建立微分方程等方式对滑坡进行预测。如李小伟等通过GM(1,1)模型对三峡库区树坪滑坡进行预测,得到的预测结果与实际结果基本一致[3]。非线性模型近年来快速发展,如BP神经网络模型、突变理论预报模型等[4]。如常晁瑜等通过BP神经网络对黄土地区滑坡进行建模预测,得到了理想的预测效果[5]。虽然以上一些方法预测效果良好,但是这些方法都具有一定的缺点,如斋藤迪孝法预测需要理想的实验条件,但是目前滑坡形成机理复杂,因此该方法不具备普遍性。而GM(1,1)模型虽然适用于目前预警,但是模型严格依赖于每一个数据,当数据缺失时模型精度变化较大,实际滑坡中数据缺失较为常见,因此该方法也难以应用。BP神经网络虽然解决了如上缺点,但是BP神经网络存在容易陷入局部最优,训练时间过长,迭代次数过多的情况[6]。

基于以上模型缺点,本文提出了优化的支持向量机模型。支持向量机原理较为简单,实现方便,运算速度快,在处理复杂非线性问题上表现良好。如李利峰等[7]通过SVM-LR融合模型对山阳县滑坡灾害易发性进行分析,得到了高精度的预测模型。

但是支持向量机模型还不完善,运算时参数是人为设置,运算精度变化较大[8]。为了减少人为设置造成的误差,提出了一种灰狼算法对支持向量机进行优化,得到了高精度模型。同时,以往得到的滑坡数据分类标准较为模糊,大多数通过专家法进行分类,此方法分类得到的数据受个人主观影响较大。同时大多数是依靠位移进行分类,但实际滑坡过程中参数种类较多,并且各个参数对分类影响均不同,为得到更客观的分类数据,本文通过熵值法对数据进行处理,从而得到客观的分类标签。

1 滑坡灾害实验平台的搭建

1.1 滑坡灾害模拟实验场搭建

滑坡灾害模拟实验场由三部分组成,如图1。分别为实验箱体、液压升降系统、控制箱。其中,实验箱体最大承载60 t泥土,规格为4.4 m×4.0 m×1.45 m。

图1 实验框图Figure 1 Experimental block diagram

1.2 数据采集系统平台搭建

数据采集系统由传感器系统和监测软件组成。考虑到滑坡形成机理的复杂性,本文使用地表位移传感器、土壤应力传感器、降雨量传感器、深层含水率传感器和浅层含水率传感器采集对应的数据。

上位机系统则将传感器发送的数据进行处理显示,并将数据保存到数据库中,方便模型数据使用,如图2。

图2 上位机界面图Figure 2 PC interface

2 熵值法结合GWO-SVM模型

2.1 熵值法

熵值法是信息论中对数据不确定性度量的一种方法[9]。一般来说,信息量越大,数据不确定性就越小,即熵越小,信息的效用值越大。通过计算各属性数据的信息熵,就能确定各属性权重。熵值法实现步骤如下。

1) 数据标准化处理

由于在数据计算时,不同指标的量纲不统一,因此需要将数据进行标准化处理,将指标绝对值转化为相对值。定义:

xij=|xij|(i=1,2,…,n;j=1,2,…,m)。

(1)

式(1)中,xij表示第i项下的第j个指标。

由于同时存在正向指标与负向指标,并且不同指标含义不同,正向指标越高越好,负向指标越低越好,因此需要分别处理。

定义正向指标:

(2)

定义负向指标:

(3)

2) 计算j项下第i个对象的特征比重pij:

(4)

3) 计算第j项熵值ej:

(5)

由式(5)可知,若第j项指标的观测差异越小,熵越大。

4) 计算第j项指标差异系数为

gj=1-ej。

(6)

当第j项指标观测值越大时,差异系数越大,表明该指标越重要。

5) 第j项指标权重系数

(7)

6) 最终计算第i个对象的综合评价值

(8)

2.2 灰狼算法

灰狼优化算法[10](Grey Wolf Optimizer,GWO),是由澳大利亚格里菲斯大学学者Mirjalili等人于2014年提出来的,后经多国学者完善的一种新型种群优化算法,它通过模拟灰狼捕食猎物的行动,包括包围猎物、追踪、狩猎等行为来实现优化。它的原理简单易懂,同时具有强收敛、参数少、易实现等特点,被广泛应用于多个领域。

2.2.1 灰狼算法的原理

灰狼是一种群居生物,狼群之间具有严格的等级制度,如图3。

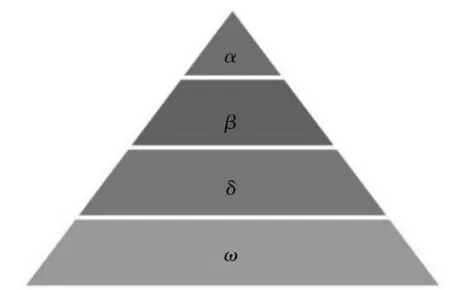
图3 灰狼等级制度图Figure 3 Gray wolf hierarchy

1) 社会等级第一层:α狼。作为狼群中的绝对支配层,该层的狼为决策狼,负责狩猎、栖息、繁衍等行为,并同时支配下三层狼。

2) 社会等级第二层:β狼。该层的狼为辅助狼,它主要辅助α狼作出决策,并且当α死亡后,它就会接替α位置成为第一层。

3) 社会等级第三层:δ狼。该层的狼是功能狼,由幼狼、哨兵狼和捕猎狼组成,是狼群的重要组成部分。

4) 社会等级第四层:ω狼。该层狼作为狼群最底层,服从所有等级高于该层的狼,避免狼群的自相残杀。

2.2.2 灰狼算法的实现步骤

1) 社会等级分层:计算狼群中每个个体的适应度,将适应度进行排序,选择适应度最好的三头狼作为α、β和δ,其余的狼全部标记为ω。构造完成的社会等级制度中,α狼、β狼、δ狼指导产生最优解。

2) 包围猎物:灰狼在搜索猎物时会不断地接近猎物,同时形成包围。它的数学模型为

(9)

式(9)中:“∘”表示hadamard乘积。A和C为协同系数向量,计算如公式所示。Xp为猎物的位置向量,X(t)表示灰狼当前位置向量,t代表迭代次数。

(10)

式(10)中:a为线性下降的数,由2降到0。r1和r2为位于[0,1]的一个随机向量。

3) 狩猎:理论上,灰狼识别猎物(最优解)的过程主要通过α狼、β狼、δ狼指导完成。但是由于很多问题的解比较复杂,其空间特征不明显,得到的解并不精确。为了得到精确最优解,假设α狼、β狼、δ狼均具备较强的捕猎定位能力,是每次迭代后保留适应度最好的三头狼,根据三头狼的位置从而逐渐确定最优解位置。定义:

(11)

式(11)中:Xα、Xβ、Xδ分别表示α狼、β狼、δ狼的位置向量。X为灰狼的位置向量。Dα、Dβ、Dδ分别表示当前狼与最优三头狼之间的距离。

(12)

式(12)中:X(t+1)表示经三头狼指导产生的候选狼的位置向量。当|A|大于1时,表示灰狼之间比较分散,从而扩大搜索猎物范围。当|A|小于1时,表示灰狼开始集中,从而搜索某个特定范围内的猎物。

如图4,候选解的位置将落在三头狼共同确定的随机圆内。即三头狼首先确定猎物大致范围,然后其他候选狼根据三头狼的指导,不断在猎物附近更新位置,形成包围圈,从而找到最优解。

图4 灰狼狩猎图Figure 4 Grey Wolf Hunting

2.3 支持向量机SVM

支持向量机[11](Support Vector Machine)是Cortes和Vapnik于1995年首先提出的,是一种基于统计学习理论的VC维理论以及最小化结构风险的机器学习方法。它在解决非线性、小样本问题上表现良好,并且原理简单、运算较快。它的本质是一种二分类模型,通过找到对应的分类器(超平面)从而将数据进行分类。

支持向量机本质为寻找最优超平面。以二分类为例,训练集样本为(xi,yi),i=1,2,…,n(n是样本点个数),其中xi为样本向量,yi为分类标记,y∈{-1,0,1},定义超平面函数

wTx+b=0。

(13)

计算样本点到超平面的几何距离为

(14)

(15)

同时,支持向量机必须满足样本点到超平面距离大于1,即

yi[(wTxi+b)]-1≥0,i=1,2,…,n。

(16)

此时,超平面问题转化为寻优问题。通过引入Lagrange函数,添加拉格朗日乘子α,并通过鞍点处极值为0计算得到参数为

(17)

理论上二维平面上的点已经可以划分,但是实际情况中,由于部分点的存在,使得无法找到对应的超平面,因此此部分的点需要舍弃,通过引入松弛变量ε,表示允许某些样本点到分类平面的距离不满足原先的要求,即

yi[(wTxi+b)]≥1-εi,i=1,2,…,n,εi≥0。

(18)

为了表征所放弃的此部分的点,引入惩罚因子C,此时超平面为

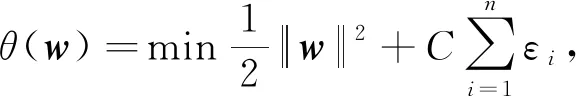
(19)

二维平面上的点经上述公式后可以得到划分。但是当样本维数较高时,超平面的选择较为困难。三维空间还可以通过选择一个曲面来进行数据划分,但是当处于四维、五维乃至更高维度时,无法计算得到对应的超平面。支持向量机通过引入核函数K来解决此问题,通过核函数的处理,高维数据线性不可分转化为了低维空间线性可分问题。

(20)

2.4 方案设计

通过模拟实验得到数据,首先进行数据预处理,得到归一化数据,通过熵值法计算各属性权值,将危险度进行划分得到对应的分类数据。再通过支持向量机与优化后的模型进行对比,得到最终实验结论。

3 实验分析

实验数据来源于中国计量大学岩土灾害模拟试验场,通过传感器采集数据,在通过软件进行输出显示与存储,通过MATLAB软件首先得到分类数据,随后进行建模分析。

3.1 数据处理

完成模拟实验后,得到的部分实验数据,如表1。

表1 部分实验数据

将数据进行熵值法处理,得到的权重表如表2。

表2 指标权重表

计算得到的危险度变化图如图5。对比危险度曲线与实验中的滑坡数据,危险度突变前后,位移、应力、含水率等数据均发生了变化,再对比实际滑坡发生过程,将0～0.25定义为低危险度,此时分类标签为1;0.25～0.50定义为中危险度,分类标签为2;0.50～1.00为高危险度,分类标签定义为3。

图5 危险度变化图Figure 5 Risk change

3.2 GWO-SVM模型验证

3.2.1 SVM模型验证

支持向量机模型中,模型参数c和g的数值对模型影响较大。c表示放弃的样本点的个数,参数g决定了寻找超平面时所需支持向量的个数,影响模型的训练与预测速度。

将熵值法分类后的数据导入SVM模型,得到的分类结果如图6。

图6 SVM模型结果Figure 6 SVM model results

通过模型预测结果可以看到,危险度划分为三类数据后,低危险度和中危险度预测结果与实际结果较为吻合,高危险度预测结果很差,多次训练后预测效果仍然较差。

分析可得,一方面是高危险度样本较少,另一方面可能受支持向量机参数的影响。

保持参数g不变,改变支持向量机的参数c,多次训练后得到的结果,如表3。

表3 参数c预测结果表

分析数据与预测结果图,当c很低时,放弃的样本点数量越多,此时容易出现欠拟合现象,模型精度大幅下降。当c很高时,表明模型越不能容忍出现误差,此时容易出现过拟合等现象,导致模型泛化性能较差。

保持参数c不变,改变参数g,训练得到的部分结果,如表4。

表4 参数g预测结果表

分析结果可得,参数g过小,平滑效应过大,训练集的准确率很低,测试集准确率也越低;参数过大,模型预测只会作用在支持向量附近,无法有效预测未知样本。

实验结果表明,人为设置参数的支持向量机模型精度较差,改变参数对实验结果影响较大,容易出现欠拟合与过拟合现象。

3.2.2 GWO-SVM模型验证

将数据导入GWO-SVM模型,经GWO优化后的c和g参数导入SVM模型,得到的实验结果,如图7。

图7 GWO-SVM预测结果图Figure 7 GWO-SVM prediction results

分析预测结果图,可以看到,低危险度、中危险度、高危险度预测结果与实际结果较为吻合,预测误差在一个样本左右。对比单一支持向量机,即使样本较少,也能得到理想的预测结果。

为避免实验结果的偶然性,多次训练后得到的对比实验结果如表5。

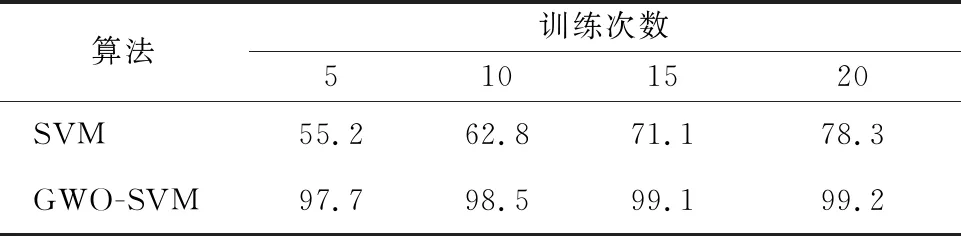
表5 GWO模型精度表

实验表明,GWO-SVM模型与SVM模型相比,预测精度有较大提升,基本稳定在97%左右,预测结果与实际结果相差个数为1～2个,并且计算过程中减少了人为设置参数的影响,能更好地对数据进行预测分类。

4 结 论

本文搭建的灾害模拟实验平台采集得到的数据反映了滑坡发生的表面与内部情况,数据具有可靠性。熵值法解决了滑坡数据分类的不确定性,通过客观的方法得到了准确数据。单一支持向量机参数c和g对模型精度影响较大,人为改变参数得到的模型精度在50%～80%左右,得到高精度模型比较困难。灰狼算法优化后的支持向量机解决了人为设置参数造成的损失,经灰狼算法优化后的支持向量机模型精度均在97%以上,训练速度快,得到的预测结果较为稳定。优化后的GWO-SVM模型能精确预测滑坡的易发性,可以广泛应用于当前复杂的滑坡灾害,减少滑坡造成的人员伤亡。