智能算法在蒸汽管网保温层厚度优化设计中的应用

2021-07-16陈宝法洪方驰

中国计量大学学报 2021年2期

陈宝法,洪方驰,徐旭

(1.中国计量大学计量测试工程学院,浙江杭州 310018;2.浙江浙能绍兴滨海热电有限责任公司,浙江绍兴 312000)

保温层厚度的优化设计是蒸汽管网设计的重要一环,保温层厚度过小会导致管网散热过大,造成不必要的热量损失,甚至还会造成人员伤亡等一系列问题[1];增大保温层厚度可相应地减少管网地散热损耗,但同时也增加了管网前期的投资成本。因此,合理的保温层厚度值是保证管网高效、安全运行的前提条件。

目前,蒸汽管网保温层厚度的设计方法常见的有经济厚度计算法、允许最大热流量法和指定温降法[2]。宋永军[3]给出了复合保温管保温层厚度、界面温度和最大热损失的计算方法,但并未给出实际工程案例分析。于淳光[4]采用理论计算与实测数据相结合的方法,选取工程常用的三种保温层厚度,分析不同管径的热损失,确定合理的保温层厚度,但论文中仅对已知厚度的保温层进行分析,没有根据管道的热损失和建设成本进行优化设计。

徐明海[5]采用随机抽样法对蒸汽管网保温层厚度进行设计,降低了投资成本,但该方法抽样区间较大,计算效率相对较低。魏立新、侯进才[6]采用序列二次规划法对保温层厚度优化后,管网总投资成本降低了5.64%,但论文没有对厚度的解集进行讨论,无法分析结果是否符合工程实际。张子波、李自力[7]运用遗传算法求解管径与保温层厚度以及有效节省总投资费用,但文中仅采用一种算法求解计算,没有进行不同智能算法适用性的比较。

本文在蒸汽管网保温层厚度优化设计中引入了不同的智能算法,通过对比改进遗传算法(AGA)、粒子群算法(PSO)、模拟退火算法(SA)在保温层厚度优化设计中解集上的表现,分析不同算法的适用性,旨在为蒸汽管网保温层的设计提供一定的参考。

1 数学模型

1.1 目标函数

蒸汽管网保温层的优化设计核心在于构建以保温层的建设成本和管网散热成本最小化为目标函数的保温层年折算成本数学模型[8]。

minZlayer=Cn1+Cn2+Cr,

(1)

Cn1=cil1(d+2δ+δil1)δil1πlj/τ,

(2)

Cn2=cil2(d+2δ+2δil1+δil2)δil2πlj/τ,

(3)

(4)

(5)

其中:Cn1、Cn2为内外层保温层年建设成本,元/年;Cr为年散热成本,元/年;d、δ为管道内径与壁厚,m;lj为管道j长度,m;cil1、cil2为内、外层保温层单位长度造价,元/m3;δil1、δil2为内、外保温层厚度,m;Q为蒸汽管网的总散热量,W;a为原煤单价,元/kg;τ为蒸汽管网运行年限;τ0为蒸汽管网的年运行时长,h/年;qm为标准煤低位发热量,29 307.6 kJ/kg;β1为热值转化率;β2为热效率;β3为单位转化系数;ΔT为管内蒸汽与外界环境的温差,K;λi为第i层保温层导热系数,W/(m·K);h1为管内蒸汽与内壁面的对流换热系数,W/(m2·K);N为管道的数量;n为保温层层数,本文中n=2;Rj为管道j外壁面与外界环境总换热热阻,K/W。

1.2 热工水力计算模型

蒸汽管网保温层厚度优化设计需考虑管网的热工水力运行。蒸汽管网的拓扑结构可用基尔霍夫第一、二定律,即节点流量守恒定律和环能量守恒定律表示:

U·m=G,

(6)

W·Δp=0。

(7)

其中,矩阵U为任意节点与区段之间的连接关系;向量m为区段的质量流量,kg/s;向量G为节点蒸汽的净质量流量,kg/s;矩阵W为各基本环路与区段的关系;向量Δp为管段的压降损失,Pa。

管段j的压力损失与流量之间的关系表达式如下:

(8)

式(8)中,εj为沿程阻力系数;ζj为管段上各阻力部件的局部阻力系数;ρ为管内蒸汽的密度,kg/m3。

同理,管段散热量与流量可表示为

Qj=cp·tj·mj。

(9)

式(9)中,cp为管网中的蒸汽定压比热容,kJ/(kg·K);tj为管段的温降,K。

1.3 约束条件

蒸汽管网水力热力约束条件如下。

1) 为保证蒸汽管网末端热用户的用汽需求,必须对单位管长的压降和温降给予一定的约束条件:

Δp≥ps,

(10)

Δt≥ts。

(11)

其中,Δp、Δt为单位管长的实际压降、温降,ps、ts为供热站与热用户之间单位管长的最大压降、温降。

2) 管段流速约束:

根据《动力管道设计手册》,管道中蒸汽的流速需要控制在一定的范围之内:

vmin≤vi≤vmax(i=1,2,3,…,M)。

(12)

其中,vi为管段i中蒸汽的实际流速,m/s;vmin、vmax为管段中蒸汽允许的最小、最大流速,m/s;M为管道数量。

1.4 优化设计方案

本文主要运用了遗传算法(GA)、粒子群算法(PSO)和模拟退火算法(SA)对管网的保温层进行优化设计。蒸汽管网保温层优化设计的流程图如图1,优化智能算法的介绍可参见文献[9-11]。

图1 保温层厚度优化设计流程图Figure 1 Flow chart of the optimized design of insulation layer thickness

由于遗传算法在全局搜索过程中存在个体随机性大、收敛慢等问题,本文进行了3点改进,提出了改进遗传算法(AGA)。

1) 选择复制过程采用中位向上优化策略,即每一代种群在复制过程中都对保温层厚度对应的适应度进行判别。若其适应度不小于种群的平均适应度,则保留该保温层厚度编码;否则选择平均适应度对应的保温层厚度编码进行复制并继续下一步。

2) 引入自适应交叉和变异概率,使得种群的交叉和变异操作可根据保温层厚度的适应度高低进行跟随调整,提高搜索效率。自适应交叉和变异概率公式如下:

(13)

(14)

其中,Fmax、Favg为种群中保温层厚度适应度最大值、平均值;Fc、Fm为交叉操作、变异操作中厚度适应度;Pc、Pm为种群中厚度的交叉、变异概率;Pc,adp、Pm,adp为种群中厚度的自适应交叉、变异概率。

3) 提出变异位置修正。变异操作中变异位置的随机性可能导致个体变异后保温层厚度不满足约束条件,即需要对种群中厚度编码的变异位置进行约束,保证变异后的厚度大小在合理范围之内。

图2给出了遗传算法(GA)和改进遗传算法(AGA)对同一管段(管径630 mm,管壁厚10 mm,管长10 m)保温层最佳厚度进行寻优的收敛过程。

由图2可见,GA算法在经过上述三点改进后,收敛的迭代次数由272次下降到6次,而且并不改变其收敛结果,说明改进后的GA算法可以有效提高收敛效率,因此在蒸汽管网保温层优化设计中可使用AGA算法代替GA算法。

图2 GA与AGA算法寻优对比图Figure 2 GA and AGA algorithm optimization comparison diagram

2 案例分析

本文针对绍兴某地一号线蒸汽管网的改造工作,开展保温层厚度的优化设计。图3为管网现有方案,管网系统所在产业用地规模约为168.92万m2,蒸汽管网呈枝状分布且均为架空敷设,共有52根管段,全长2 161 m,分别供给十个热用户点(U1～U10),供热能源站的蒸汽流量为213.2 t/h,蒸汽温度为304 ℃,蒸汽压力为0.616 MPa。

图3 绍兴某地一号线蒸汽管网布局图Figure 3 Layout of the steam pipe network of Shaoxing Line 1

2.1 模型验证

图4～图6给出了该蒸汽管网现有方案的热用户流量、温度、压力的实测值,本文的计算结果以及某公司软件结果的比较。由图可见,各个热用户蒸汽流量和压力的计算结果与实测值相对误差不超过5%,均在合理范围之内;温度的计算结果与实测值误差最大为10.662%,但本文模型对温度的计算结果与某公司软件的温度计算结果相对误差均小于1%,说明管内蒸汽状态复杂难以确定,蒸汽温度计算误差偏大,但总体上符合管网的热工计算要求,说明本文的数学模型可用于管网的水力热力计算。

图4 各热用户蒸汽流量对比图Figure 4 Comparison chart of steam flow of various thermal user

图5 各热用户蒸汽压力对比图Figure 5 Comparison chart of steam pressure of various thermal users

图6 各热用户蒸汽温度对比图Figure 6 Comparison chart of steam temperature of various thermal users

2.2 参数设置

绍兴某地一号线蒸汽管网保温层厚度优化设计中,选取当地环境温度为20 ℃,环境风速为1 m/s。本案例中蒸汽管道管径组合为

DN={57,89,108,133,159,219,273,325,377,426,478,529,630,720,820,1020}(其中DN为管道的公称直径,mm),案例中管网的保温层为内外两层设计,依据《工业设备及管道绝热工程设计规范》,为考虑到维修人员工作的安全性,将复合保温层的界面温度设为100 ℃,外表面温度设为50 ℃。蒸汽管道由内到外的热流量相等,因此可得下式:

(15)

式(15)中:Q为管道径向散热的热流量,W;l为管道的长度,m;A为管道外壁面与环境的换热面积,m2;λ1、λ2分别为内、外保温层的导热系数,W/(m·K);h为管道外壁的表面传热系数,W/(m2·K);Δt1、Δt2、Δt3分别为内、外保温层温降以及外壁面与环境的温差,℃;d1、d2、d3分别为工作钢管、内保温层、外保温层的外径,mm。

以案例中管网的供热工况为例,根据式(15)可计算得到不同管径对应的保温层最低厚度推荐值(从大到小)依次为:

δ1={78,71,68,64,60,57,55,52,49,46,42,36,34,31,29,24};

δ2={30,27,26,24,22,21,20,18,17,15,13,11,9,9,8,7};

其中,δ1为内保温层最低厚度,δ2为外保温层最低厚度,单位mm。

设置各算法的最大迭代次数均为500次,其他参数设置如表1。

表1 智能优化算法的预设参数

2.3 结果分析

2.3.1 不同保温层方案比较

图7为优化计算后不同保温层厚度组合方式下蒸汽管网各管段的温降情况,表2为不同组合方案所对应的管网散热量和保温层年折算成本。

由图7和表2可见三种算法设计得到的管网保温层方案虽增加了管网保温层的建造成本,但均能有效减少管网系统管段的散热量,降低整个管网系统热量损耗,且均降低了保温层年折算成本。

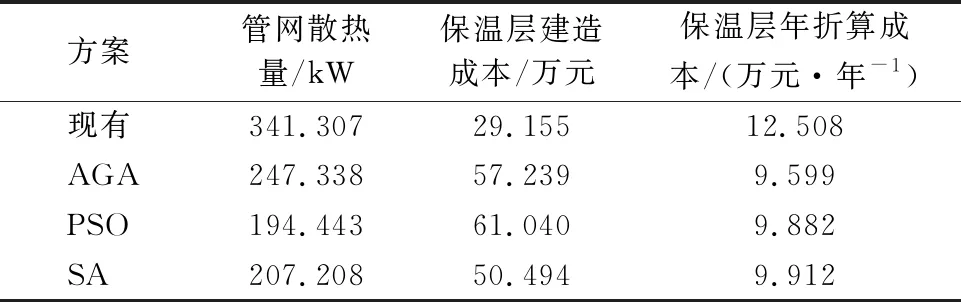
表2 不同方案计算结果对比

图7 优化前后管网温降对比图Figure 7 Comparison of pipe network temperature drop before and after optimization

AGA算法求解得到的方案中保温层年折算成本最低,但管网的散热量在三种优化方案中最大,且保温层的建造成本较高;PSO算法优化方案的管网散热量最低,仅为194.443 kJ/s,但其保温层的建设成本为三者中最大,且保温层年折算成本相比于AGA算法方案多0.283万元/年;SA算法优化方案的保温层建造成本为三种方案中最低,仅为50.494万元,但仍高于现有方案,管网散热量和保温层年折算成本也较高。接下来从不同算法收敛的解集角度对不同的蒸汽管网保温层厚度方案进行评估。

2.3.2 保温层厚度优化结果比较

图8、图9给出三种智能优化算法计算得到的蒸汽管网各管段内外保温层厚度的寻优结果。

图8 内保温层优化结果对比图Figure 8 Comparison of optimization results of inner insulation layer

通过对图中内外保温层优化结果分析可知,AGA算法由于个体解的随机性,因此生成的部分管道保温层厚度值小于推荐值的最低厚度,不符合实际设计需求。PSO算法和SA算法寻优获得的内保温层厚度方案相同,且均为对应管段的最低厚度值。其中PSO算法寻优获得的外保温层厚度比同管段其它算法求得的厚度大,而且相同管径对应的外保温层厚度的大小也各不相同。相较之下,SA算法建议相同管径内外保温层厚度采用相等的值。因此从实际工程建设角度出发,应选用模拟退火(SA)算法优化得到的蒸汽管网保温层厚度方案。

通过对比SA算法计算得到的内外保温层厚度和现有方案的厚度,在对该蒸汽管网改造时可采取适当地减少内保温层厚度、增加外保温层厚度的优化设计建议。