基于光纤干涉投影的子孔径拼接测量方法

相 超,王道档,窦进超,孔 明,刘 璐,许新科

(中国计量大学 计量测试工程学院,浙江 杭州 310018)

三维面形检测技术在工业制造、生物影像与机器视觉等方面中均发挥着重要的作用,而大口径复杂曲面因有改善像质、简化仪器结构等优点在光学成像系统中得到了广泛的应用[1]。目前常用的三维面形检测方法有坐标测量法、光学干涉仪、计算全息法、结构光测量法以及光纤干涉投影测量法等[2]。坐标测量法主要是利用触针对被测面形进行逐点测量,通过扫描获取各点三维坐标并拟合获取全口径面形,在测量被测面时容易对其造成划伤,且其单点采样的测量方式使其测量效率受限[3-4]。光学干涉仪具有高空间分辨率与高检测精度的优点,但其易受环境影响且动态范围较小[5]。计算全息法是一种高精度的非接触式零位干涉测量法,但是其补偿测量模式导致该法测量成本高、通用性较差[6]。结构光测量法具有系统结构简单的优点,但其检测精度受限于投影装置的分辨率[7]。光纤干涉投影测量法因其简便的检测过程、较高的检测精度,在各类复杂曲面的面形测量中得到越来越来广泛的应用;但是由于光纤探头所投射光斑范围尺寸与光强的限制,该方法的测量口径与动态测量范围有限[8]。

为了进一步实现大动态测量范围复杂光学元件的面形检测,子孔径拼接测量法顺势而生。其原理是将被测面形划分为多个相对较小的子孔径区域,分别检测各子孔径的面形数据,将所测得各子孔径数据进行拼接来获取全口径面形[9]。目前子孔径划分方式通常为圆形或方形等规则形状[10-11],但是在对大动态范围复杂曲面进行测量时,规则形状的子孔径划分形式灵活性不高,且拼接效率较低。

为了满足大动态范围复杂曲面面形的测量需求,本文提出基于光纤干涉投影的子孔径拼接测量方法。根据被测物的曲面特征进行子孔径划分,并利用所提出的光纤干涉投影测量系统对各子孔径分别进行测量并计算获取其对应的面形数据,进而对各子孔径面形数据进行拼接来获取全口径拼接面形。同时提出了基于子孔径重叠区域特征与位姿的加权算法,来改善拼接面形的“拼接痕迹”。为验证所提方法的可行性,进行了仿真分析与实验验证。结果表明该检测方法具有精度较高、动态测量范围大等特点,可满足大口径复杂曲面的检测需求。

1 原 理

1.1 系统光路布局

图1为基于光纤干涉投影的面形测量系统光路布局。单纵模激光器发出的激光光束(光波长为532 nm)经偏振片和1/2波片(HWP)后变成线偏振光,该线偏振光入射至偏振分光棱镜(PBS)后分成p分量透射光、s分量反射光。其中,透射p偏振光通过光纤耦合器1耦合进单模保偏光纤SF1;反射s偏振光经过一快轴方向与x轴方向的夹角为45°的1/4波片(QWP)后,垂直入射至安装在压电陶瓷(PZT)装置上的反射镜,经其反射并原路返回,返回后的反射s偏振光再次通过1/4波片QWP和偏振分光棱镜PBS,随之被光纤耦合器2耦合进入单模保偏光纤SF2。

图1 基于光纤干涉投影的子孔径拼接测量系统布局图Figure 1 System layout of sub-aperture stitching testing system based on fiber optic interference projection

单模保偏光纤SF1与SF2的出射端分别作为点光源,将二者以平行且共面的状态安装在一个光学测量探头内,使得两点光源在三维空间内产生干涉[12],该探头出射端的干涉条纹将投射至被测物表面。将光学探头安装在多轴调整架上,利用五轴调整架作为子孔径扫描机构,通过调节光纤投射端的位姿来改变投射至被测面形各区域(子孔径)干涉条纹的密集程度,通过解调可得到该子孔径的面形信息,由此实现被测元件全口径覆盖。计算机(PC)一端连接压电陶瓷(PZT),通过控制PZT产生的微位移来改变光程差以实现多步移相干涉;另一端连接CCD相机,控制相机来实时采集含有被测物形貌信息的干涉条纹图案。

1.2 光纤干涉投影测量原理

图2为以相机成像平面、干涉条纹接收屏与光纤投射端建立光纤干涉投影检测系统模型。在该模型中,设相机平面为XY平面,CCD相机光轴方向为Z轴,并设Z轴与条纹接收屏的交点为坐标原点O;以相机成像平面的中心Oi建立像平面坐标系,设像素点的水平和竖直方向分别为m、n轴,分别表示像平面横纵坐标信息。

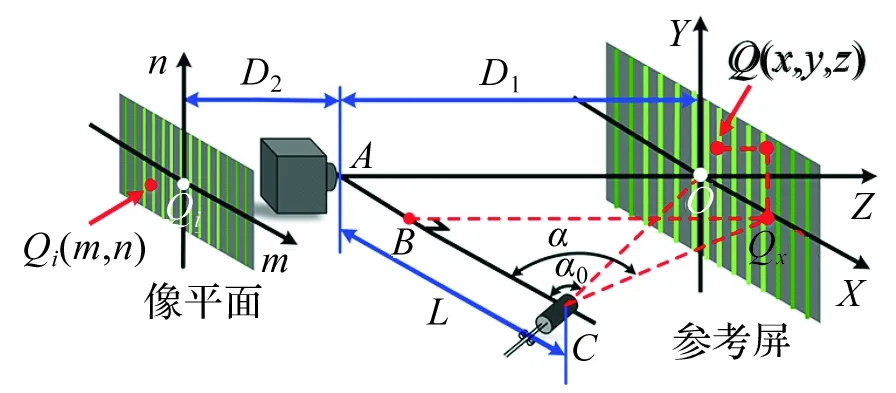
图2 光纤干涉投影系统原理图Figure 2 Schematic diagram of fiber-diffraction interference projection testing system

取被测物表面上任意一点Q(x,y,z),通过相机成像原理可得点Q(x,y,z)与其像平面坐标系内点Qi(m,n)之间的关系为

(1)

式(1)中,D1为相机镜头中心A与坐标原点O之间的距离,D2为点A与点Oi间的距离。点Q(x,y,z)在X轴上的映射点Qx的坐标值与投射端的投射角度α之间关系可表示为

z=D1+tanα·(L-x)。

(2)

式(2)中,L为相机镜头中心A与投射端中心C之间的距离。由式(1)与式(2)可将点Q(x,y,z)的坐标信息表示为

(3)

式(3)中,m,n为点Q(x,y,z)对应的像平面坐标信息,它可利用CCD相机采图后直接获取。投射角α则可通过对干涉图进行解调后获取相位信息来得到。其中,相位信息φ(x,y,z)与投射角α间的关系为

(4)

然而当被测物的梯度范围较大或其口径较大时,会出现经被测物调制后的干涉条纹过于密集而无法解调的问题,或出现无法一次性获取被测物全口径的干涉条纹。因此,可对被测物部分区域(子孔径)分别进行检测,再将各子孔径拼接来获取全口径面形。

1.3 子孔径划分及拼接原理

在图1的光纤干涉投影测量系统中,经CCD相机采集到的干涉条纹图为了能够清晰可辨,根据奈奎斯特采样定理,可将相机的空间截止频率与干涉条纹图的频率的关系作为所采集干涉条纹是否清晰可分辨的依据[13-14]。当被测面形的斜率范围过大致使干涉条纹不满足CCD相机可分辨条件,但又避免因过分提高器件性能产生的费用,可通过对被测元件各部分区域(子孔径)分别进行测量,再通过拼接算法将其拼接来实现全口径测量。

通过调整五轴调整架来改变光纤探头的位姿,使得被测区域上所投射干涉条纹的空间频率均满足可分辨条件。再通过电脑控制PZT产生微位移来实现多步移相,其次控制CCD相机逐次采集各子孔径的干涉条纹信息,直至能够覆盖全口径面形。在子孔径划分设计中应确保子孔径的数目尽量少、且子孔径间重叠区域不小于1/4子孔径区域的原则[15]。

在实际测量中,由于光纤探头的移动会导致不同子孔径之间产生倾斜、平移和离焦误差。因此需要计算各子孔径间对应的倾斜、平移和离焦系数,通过上述拼接系数将各子孔径数据变换到统一坐标下进行拼接处理。对于任意两个重叠区域的子孔径,其面形之间的关系可表示为

ΔWi,j(x,y)=ai,jx+bi,jy+ci,j(x2+y2)+pi,j。

(5)

式(5)中,ΔWi, j(x,y)表示子孔径i与子孔径j间重叠区域的面形数据,ai, j表示两子孔径在x方向的倾斜系数,bi, j为y方向的倾斜系数,ci, j为离焦系数,pi, j为平移系数。

由于测量中存在误差,所有子孔径间重叠区域必然无法全部满足式所表征的关系。因此我们定义子孔径间的重叠区域面形平方和作为目标函数F,所以有

(6)

根据最小二乘法,在F取最小值时可求取得到各子孔径间的拼接系数,最终将各个子孔径的面形数据转换到统一坐标下,从而实现全口径的面形检测。

2 重叠区域分区域加权计算法

如上所述,按照最小二乘法获取的拼接系数可将各子孔径的面形数据统一到同一坐标系下,再将各子孔径相加并对重叠区域进行取均值操作即可获取全口径面形检测结果。但是在子孔径间重叠区域数据的计算处理中,利用传统均值计算法[16]获取的拼接面形难免会产生“拼接痕迹”,为进一步实现拼接面形的平滑过渡,可依据重叠区域的特征和位姿状态采用分区域的加权计算法。下面将重叠区域分为单连通域与非单连通域进行分析。

2.1 单连通重叠区域

以图3任意两个具有重叠区域(单连通域)的子孔径为例,设该重叠区域的质点为P1,以点P1与距其最远点P2两点间连线P1P2与x轴正半轴夹角的绝对值β作为任一重叠区域位姿方位角的表征值。

图3 两子孔径及其重叠区域(单连通域)示意图Figure 3 Diagram of two sub-apertures and their overlapped region(simply connected domain)

同时按照该子孔径间重叠区域相对于x轴的位姿分布特征,可设定方位临界值β0(如β0= π/4)。依据方位角与方位临界值之间的关系,对重叠区域选取相应的渐变系数来计算表征该重叠区域。当方位角β>β0时,取在重叠区域任一横坐标区间[x1,x2]内渐变系数为kx;当方位角β≤β0时,取在重叠区域任一纵坐标区间[y1,y2]内渐变系数为ky。因此有

(7)

因此,两子孔径间重叠区域的面形W可表示为

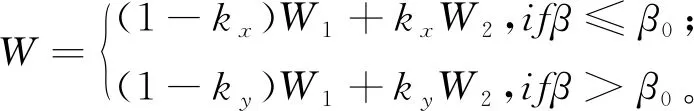
(8)

式(8)中,W1、W2分别为任意两个子孔径在重叠区域内的面形数据。

由式(7)和式(8)可得,任一重叠区域内的渐变系数变化趋势均为平滑上升的曲线,因而能够有效地避免因重叠区域边缘点突变导致的“拼接痕迹”[17]。其次当渐变系数为kx时,由kx的变化趋势可得,越靠近重叠区域任一区间端点x1时造成“拼接痕迹”的面形数据W1的权重越低,越靠近重叠区域任一区间端点x2时造成“拼接痕迹”的面形数据W2的权重越低;当渐变系数为ky时,同理如上。因此利用上述处理方法可以改善“拼接痕迹”,实现拼接面形的平滑过渡。

2.2 非单连通重叠区域

而当重叠区域为非连通域时,图4为任两个子孔径及其非单连通的重叠区域示意图。

图4 两子孔径及其重叠区域(非单连通域)示意图Figure 4 Diagram of two sub-apertures and their overlapped region(non-simply connected domain)

若对整个重叠区域进行加权计算,则区域Ⅱ的右边界与区域Ⅲ的左边界无法实现与子孔径W2之间的平滑过渡。因为对于此类非单连通的重叠区域,可对其进行分区域计算。将重叠区域沿坐标轴方向(本文以x轴为例)进行区域划分(如图4中虚线所示),将重叠区域划分为单连通区域Ⅰ、Ⅱ、Ⅲ、Ⅳ,将各划分后的单连通域按照其区域的位姿状态,分别进行加权计算,从而可实现子孔径间全部重叠区域的平滑过渡。

3 仿真及其结果分析

为验证所提出方法的可行性,对建立的光纤干涉投影检测系统进行仿真分析。在仿真中,将两光纤的纤芯距设为0.125 mm,被测对象是一随机生成面形,其设计口径为4 mm的曲面(PV值为25.76 mm),并对其施加了一定的Zernike面形误差。在仿真中模拟理想点光源的干涉过程,投射到被测表面各个区域调制后得到相应的变形干涉条纹,通过调整两点光源的位姿,使其光程差改变进而获取原干涉条纹不可分辨区域(子孔径)清晰可辨的干涉条纹,对各子孔径逐次采集满足条件的干涉条纹,进而实现全口径测量。图5为通过经被测面调制后的干涉条纹及其对应的各子孔径变形干涉条纹,其中,图5中的虚线部分内为其不可分辨的干涉条纹区域。

图5 仿真中干涉条纹及对应各子孔径区域Figure 5 Fringe patterns and corresponding sub-apertures in simulation

按照子孔径划分原则,将被测面形划分为2个子孔径,利用相机成像原理得到各子孔径在像平面上所成的像。利用解包裹算法得到该区域干涉条纹对应的相位信息,最后由相位分布与被测物表面三维信息之间的映射关系可重构各子孔径的面形数据,图6为各子孔径的面形数据及其在全局位置的分布图。

图6 仿真中子孔径面形数据及其在全局位置分布Figure 6 Surface data and its global position for each sub-aperture in simulation

利用所提基于加权计算的拼接算法对各子孔径进行拼接(各个子孔径矩阵维度均为601×601,其所需拼接时间约为0.3 s),最终得到的拼接面形如图7(a),其RMS与PV值分别为5.300 5 mm、25.761 3 mm;被测曲面的全口径真实面形如图7(b),其RMS与PV值分别为5.300 4 mm、25.760 0 mm;以上两者对应的残差分布如图7(c),其RMS与PV值分别为1.845 8 μm、7.249 0 μm。

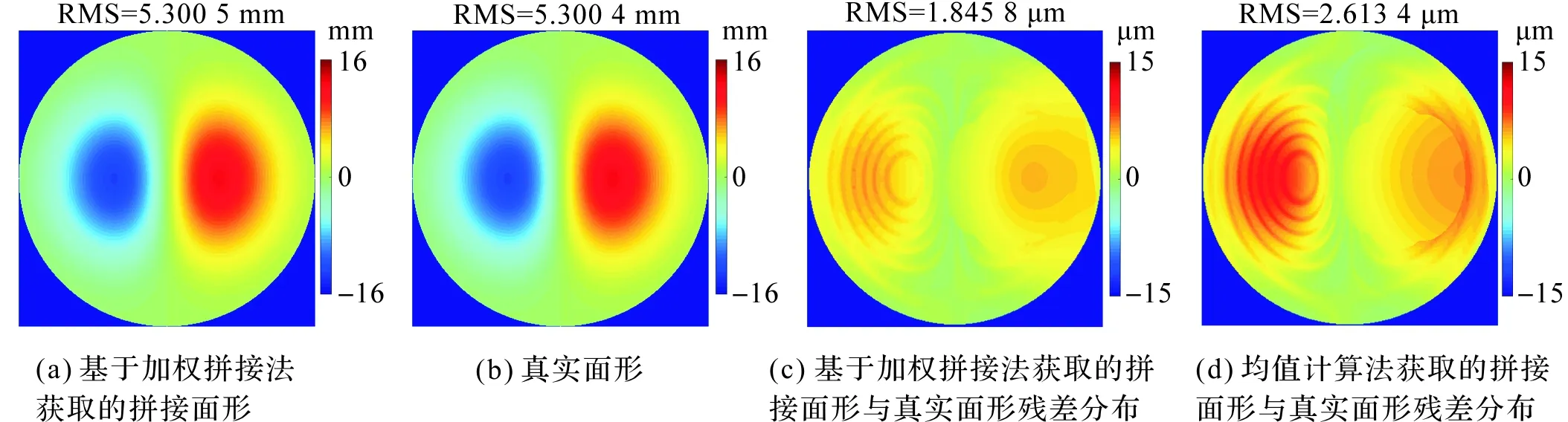
图7 仿真中拼接面形与残差分布Figure 7 Stitched surfaces and corresponding residual errors in simulation

同时传统均值计算拼接法[16]获取的拼接面形与真实面形的残差分布如图7(d),其RMS与PV值分别为2.613 4 μm、12.383 4 μm。由图7可知,利用本文所提出拼接方法获取的全口径面形与全口径真实面形结果在面形形状和量值上均具有良好的一致性,并且其残差分布效果明显优于传统均值计算法的残差分布。

4 实验测量

为了验证本文所提基于光纤干涉投影技术的子孔径拼接测量方法的可行性,搭建了如图1的子孔径拼接测量实验系统。其中,实验中所使用的单纵模激光器的波长为532 nm;CCD相机的分辨率为1 920×1 080,像元尺寸为5.5 μm×5.5 μm。测量对象为一长度约为24.5 mm、宽度约为23.1 mm、高度约为5.9 mm的粗糙石膏材质模型。

实验中将被测物按照曲面特征划分为两个子孔径,通过调节激光探头的位姿状态,利用CCD相机分别采集经被测区域调制的干涉条纹,图8为经CCD相机采集的干涉条纹图。其中,红色实线方框内的部分为利用阈值(频率阈值设定为18 pixels)进行限定后所得各子孔径区域。

图8 实验中所采集干涉条纹及对应子孔径区域Figure 8 Fringe patterns and corresponding sub-apertures in experiment

将限定后的各子孔径干涉条纹图进行解调与计算,进而得到其对应的面形数据,图9为各子孔径的面形数据及其在全局位置分布。

图9 实验中子孔径面形数据及其全局分布Figure 9 Measured surface data and its global position for each sub-aperture in experiment

利用本文所提基于加权计算的子孔径拼接法对各子孔径进行拼接(该子孔径矩阵维度为1 920×1 080,其所需拼接时间约为1.2 s),图10(a)为最终获取的全口径拼接测量结果,其对应的RMS和PV值分别为1.632 6 mm、5.914 9 mm。图10(b)为基于均值计算法[16]获取的拼接面形,其对应的RMS与PV值分别为1.820 4 mm、5.980 9 mm。

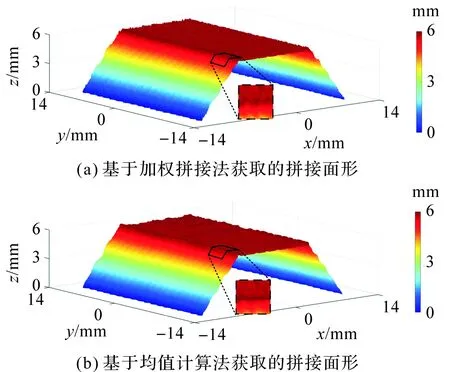
图10 实验中所测得拼接面形Figure 10 Stitched surface in experiment

由图10可以看出,相对于传统均值计算法,通过本文所述方法获取的拼接面形具有更好的面形平滑度,且无“拼接痕迹”。

5 结 论

本文针对大动态范围复杂元件的面形检测需求,提出了一种基于光纤干涉投影的子孔径拼接测量方法。以CCD相机与干涉条纹间的关系来判别干涉条纹是否清晰可辨,并以此来进行子孔径划分。在子孔径拼接算法中,提出了基于子孔径间重叠区域特征与位姿的分区域加权算法。为验证所提方法的有效性,对一大动态测量范围的被测物进行仿真分析与实验验证。结果表明,本文所提方法获取的拼接面形的与全口径真实面形具有良好的一致性,两者间残差的RMS、PV值为1.845 8 μm、7.249 0 μm;且相较于均值法获取的拼接面形有效的改善了“拼接痕迹”。该测量方法改善了光纤干涉投影法由于投射光斑范围尺寸及光强导致的测量口径与动态测量范围有限的问题,同时利用所提加权计算法改善了传统均值法在重叠区域边缘位置因无法实现平滑过渡引起的“拼接痕迹”,为大口径复杂曲面提供了一种动态测量范围大、检测精度较高的非接触式面形检测方法。在后续的工作中,可利用位姿优化或基于图像特征的子孔径定位方法来减少子孔径的定位误差,通过优化拼接算法来提高拼接效率及拼接系数的准确度。