基于门控循环神经网络的阀门泄漏检测方法

余吉超,姚 燕,欧阳航

(中国计量大学 计量测试工程学院,浙江 杭州 310018)

阀门是管道系统中的基本部件,通过控制阀门可以改变流体介质的压力和流量变化。对绝大多数阀门来说,泄漏是主要的破坏形式,其中最常见的是由于密封性差或器件老化所导致的阀门内漏和外漏。阀门泄漏不仅会造成经济方面的损失,易燃、易爆、有毒气体的泄漏还会对人身安全造成巨大威胁,因此迫切需要实现阀门泄漏故障的及时检测。目前,阀门外漏故障有一套成熟的检测技术,但阀门内漏依然主要依赖于传统检测方法,如人工巡检、超声波检测、红外测温法等。这些方法均存在一定的缺陷,如人工巡检需要手动拆卸阀门进行检查而耗费大量的人力,红外测温法受环境局限较大,超声波检测法对于微小泄漏的检测存在缺陷。

传统方法的局限性使得许多学者将声发射技术应用到阀门内漏的检测上。阀门内漏检测的首要工作就是认识内漏声源产生的机制。张颖[1]对气体内漏过程动态流体源的声源特性进行了理论分析,并用四极子声源近似表示阀门气体内漏喷流噪声源,同时建立了阀门气体内漏喷流噪声声源强度的流动参量描述方程。在理论模型的基础上,Prateepasen[2]等提出了一种基于声发射技术的新型理论模型来预测泄漏率;高倩霞[3]等基于最小二乘法建立了基于声发射信号特征的阀门泄漏故障特征参数与阀门泄漏状态的定量关系;邹兵[4]等建立了预置缺陷闸阀内漏模拟试验平台,利用小波分析技术,研究了内漏声发射信号频率分布规律;YAN[5]等通过最近邻节点算法(K-NearestNeighbor,KNN)和支持向量机(Support Vector Machine,SVM)等分类算法对阀门状态进行分类。

近年来,随着机器学习研究的不断推进,研究人员利用机器学习方法对声发射信号进行处理,有效提高了阀门的最小可检测泄漏量。如雷红祥[6]开发的阀门内漏检测装置在实验现场测得球阀内漏流量为1.6 L/min;张庚[7]通过搭建检测实验平台测得旋塞阀内漏流量为0.87 L/min;吴石恩[8]基于支持向量数据描述方法,测得最小可检测泄漏量为0.328 L/min;周文[9]基于深度置信网络评估得到阀门最小泄漏率为0.416 L/min。

尽管存在以上进展,但上述方法大都从频域的角度开展研究。考虑到阀门声发射数据可以在一定时间段内体现出阀门内漏的发展趋势,可以用时间序列模型对阀门内漏趋势进行预测。因此,本文提出了基于声发射技术和门控循环神经网络(Gated Recurrent Unit,GRU)[10-11]的阀门内漏监测方法,利用声发射技术在动态检测以及GRU在时间预测方面的优势,期望能够提高阀门所能检测到的最小泄漏量,从而实现阀门泄漏的更准确检测。

1 门控循环单元神经网络原理

GRU是一种新型的循环神经网络(Recurrent Neural Network,RNN)[12]。传统的神经网络在对序列信息进行预测时,无法基于长时间序列建立模型,而循环神经网络可以通过将信息进行循环操作,保持信息持续存在来解决上述问题。最典型的RNN方法是长短期记忆网络(Long Short-Term Memory,LSTM)[13]。相比于传统RNN网络以及其他深度网络,LSTM对数据时序性的适应能力更强,但LSTM网络存在参数量较多、模型收敛速度较慢等缺点。作为LSTM的一个变式,GRU简化了LSTM的内部单元结构,在保证较高预测精度的同时可有效缩短模型的训练时间,因此得到了广泛关注。GRU由一系列的门控循环单元构成,其中单个门控循环单元的结构示意图如图1。

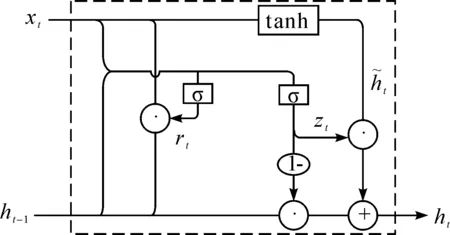
图1 门控循环单元示意图Figure 1 Schematic diagram of gated loop unit

(1)

rt=σ(W(r)xt+U(r)ht-1),

(2)

(3)

(4)

2 阀门内漏声发射检测实验及数据预处理

2.1 阀门内漏声发射检测实验

为实现基于声发射的阀门内漏检测,本文设计了对应的实验系统,如图2。实验系统主要由高压氮气钢瓶、压力表、控制球阀、待测阀门、流量计、声发射传感器、前置放大器、信号采集处理终端组成。

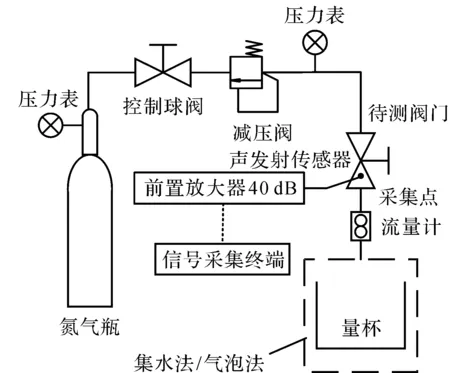
图2 阀门内漏声发射检测实验系统的设计图Figure 2 Design drawing of valve internal leakage acoustic emission detection experimental system

实验中用到的发射传感器是由北京声华科技公司生产的SR150N型声发射传感器,检测频率为22～220 kHz。为其配套的前置放大器增益为40 dB,分辨率为16 bit。前置放大器的作用是将声发射传感器采集到的极微弱的信号通过模拟电路进行放大,以便后续信号处理终端对信号进行采集。声发射传感器固定在待测阀门的外侧阀壁上,当调节阀门时,采集声发射信号到采集终端中进行进一步的处理。

采用0.2 MPa,0.3 MPa,0.4 MPa,0.5 MPa,0.6 MPa,0.7 MPa共6组压力进行实验,测试采用DN8球阀,通过调节球阀开度调整泄漏流量,采用流量计进行测定。在泄漏率为0.2 L/min、0.4 L/min、0.6 L/min、0.8 L/min、1 L/min、1.2 L/min的情况下进行实验,每个压力值下5组实验,得到了不同工况下声发射信号数据。

2.2 小波包信号降噪研究

阀门内漏检测方法由图3,固定于阀门壁上的声发射传感器将采集到声发射信号转换为电信号,并经过前置放大器放大。此时的信号包含大量环境噪声,需要对其进行降噪处理,之后再经由深度学习模型对信号进行诊断,判断阀门内漏状态。

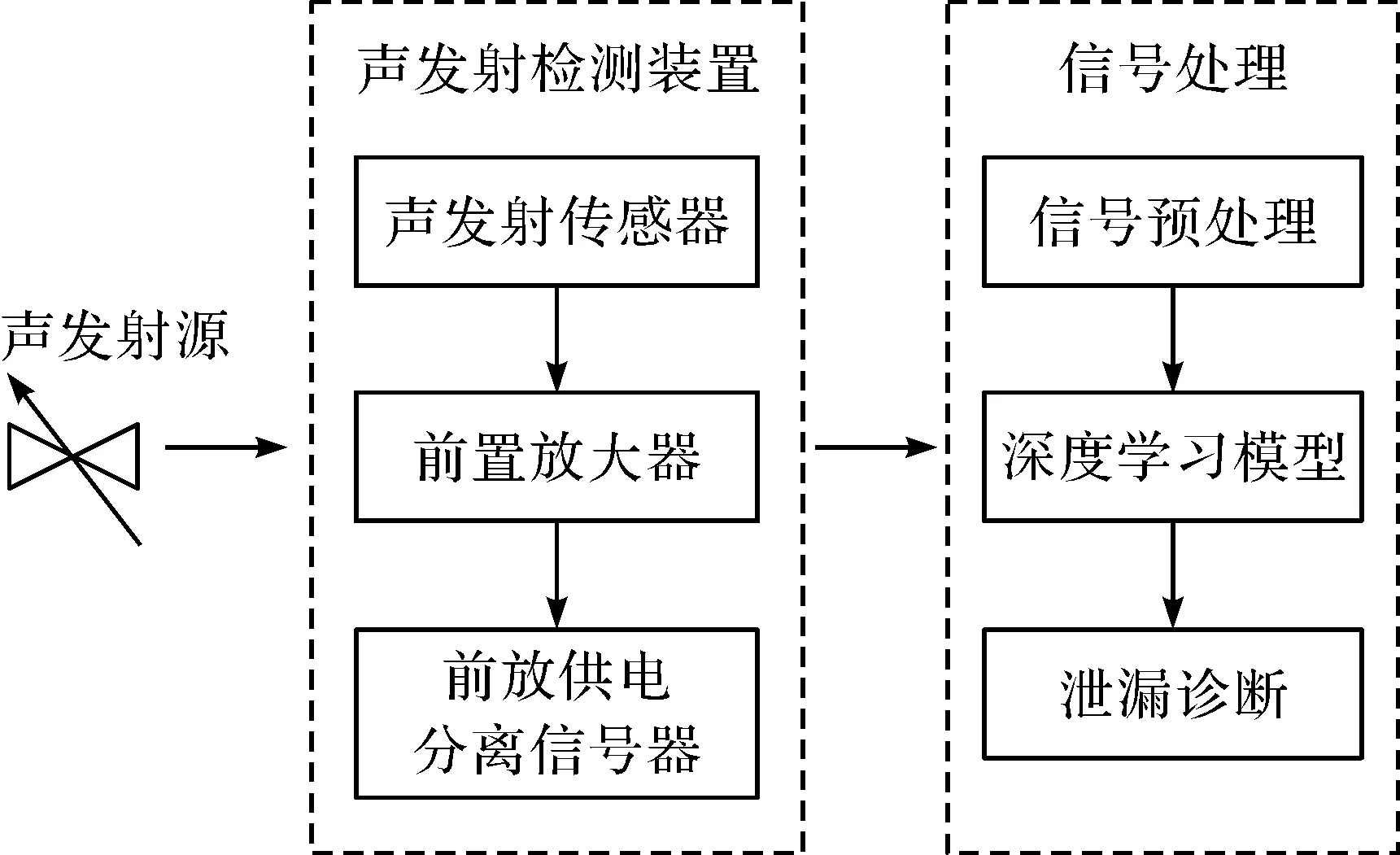
图3 阀门内漏检测方法Figure 3 Valve internal leakage detection method

小波包分解是一种常用的信号频谱分析方法,通过对信号的多次迭代,将其按频率逐层分解。相比于小波分解,小波包分解更为精细,它在分解的过程中不仅对低频信号再分解,对高频信号也会再实施分解,因此更适用于信号高频部分的分析[14]。在小波包分解的过程中,依据特点不同,不同的小波基函数对小波包分解的效果有很大影响,选择合适的小波基函数就显得相当重要。

常用的小波基函数主要包括haar小波、db小波、bior小波、coif小波、sym小波等,如表1。

表1 小波基函数特性比较

考虑到阀门内漏声发射信号复杂且数据量较大,采用具有双正交性的对称小波函数可以让信号在多尺度分解和重构中尽量不出现边缘失真。另外,为了获取信号的局部特征,应尽量选用具有紧撑性的小波函数。因此,针对阀门声发射信号,本文采用db小波作为小波包分解重构的小波基函数。基于db小波的分解结果如图4。

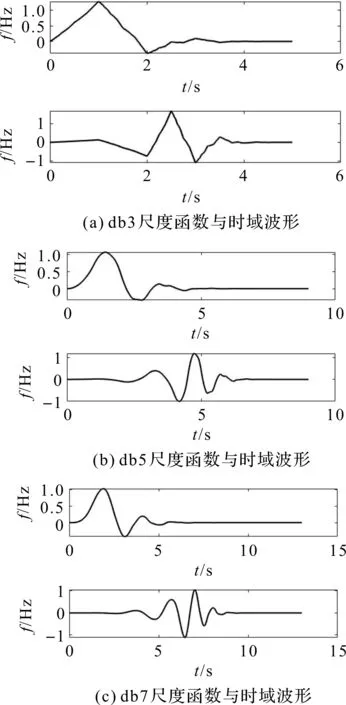
图4 db-N小波的尺度函数与时域波形Figure 4 Scaling function and time-domain waveform of db-N wavelet

由图4可知,不同阶数下的db小波的尺度函数趋势几乎没有变化,只是在光滑度上随阶数变高也在不断变高。而在不同阶数的db小波函数图像上也几乎没有变化,仅有光滑度随阶数提升不断提高。由此可见,不同阶数的db小波图像本质是类似的。dbN小波消失矩阶数为N,高阶db小波的消失矩过大不利于计算,不适用于阀门泄漏声发射信号处理。

选择db3～db5、coif3～coif5、sym3～sym5小波包基函数,分解尺度为4对信号进行降噪处理,不同小波包基函数降噪后信号的信噪比结果如图5。由图可知db小波具有更高的信噪比,且当阶数为3时,取得最好效果。

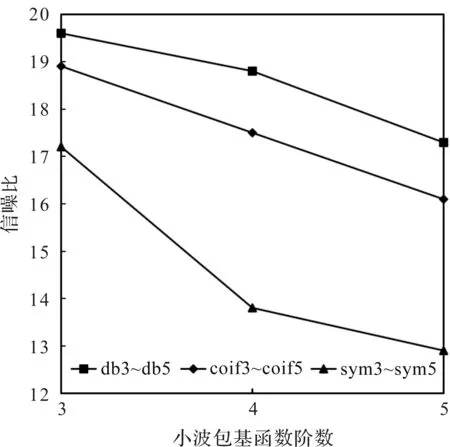
图5 不同小波包基函数下降噪对比结果Figure 5 Comparison results of different wavelet packet basis functions for noise reduction

由于存在噪声干扰,无法直接从时域图上对声发射信号进行确认。因此,需要从频域的角度进行分析,确认声发射信号的确切频率范围。结合上述分析和实验对比结果,本文利用db3小波对阀门泄漏声发射信号进行4层分解,观察不同频域段信号能量占总能量的比例,以确认声发射信号所在频域。

为确认声发射信号所在频段,需要在不改变声发射传感器与阀门的相对位置的情况下,仅仅控制阀门的开度,采集未发生和已发生泄漏时的声发射信号。将其进行小波包分解后,计算不同频段能量占总能量的比例。由图6所示,横坐标为将0到300 kHz频率范围内的信号进行4层小波包分解后的16个窗口频率窗口;纵坐标为各频率窗口能量占总信号能量的百分比。在引入声发射信号后,能量分布从56.25～93.75 kHz频段,集中到0～18.75 kHz频段。可知声发射信号能量的加入,使得0～18.75 kHz频段能量占比大幅增加,56.25～93.75 kHz频段能量占比相对减少。由此可以确认阀门声发射信号所在频段为0～18.75 kHz,而原先集中在56.25～93.75 kHz频段的信号可以认为是环境噪声。

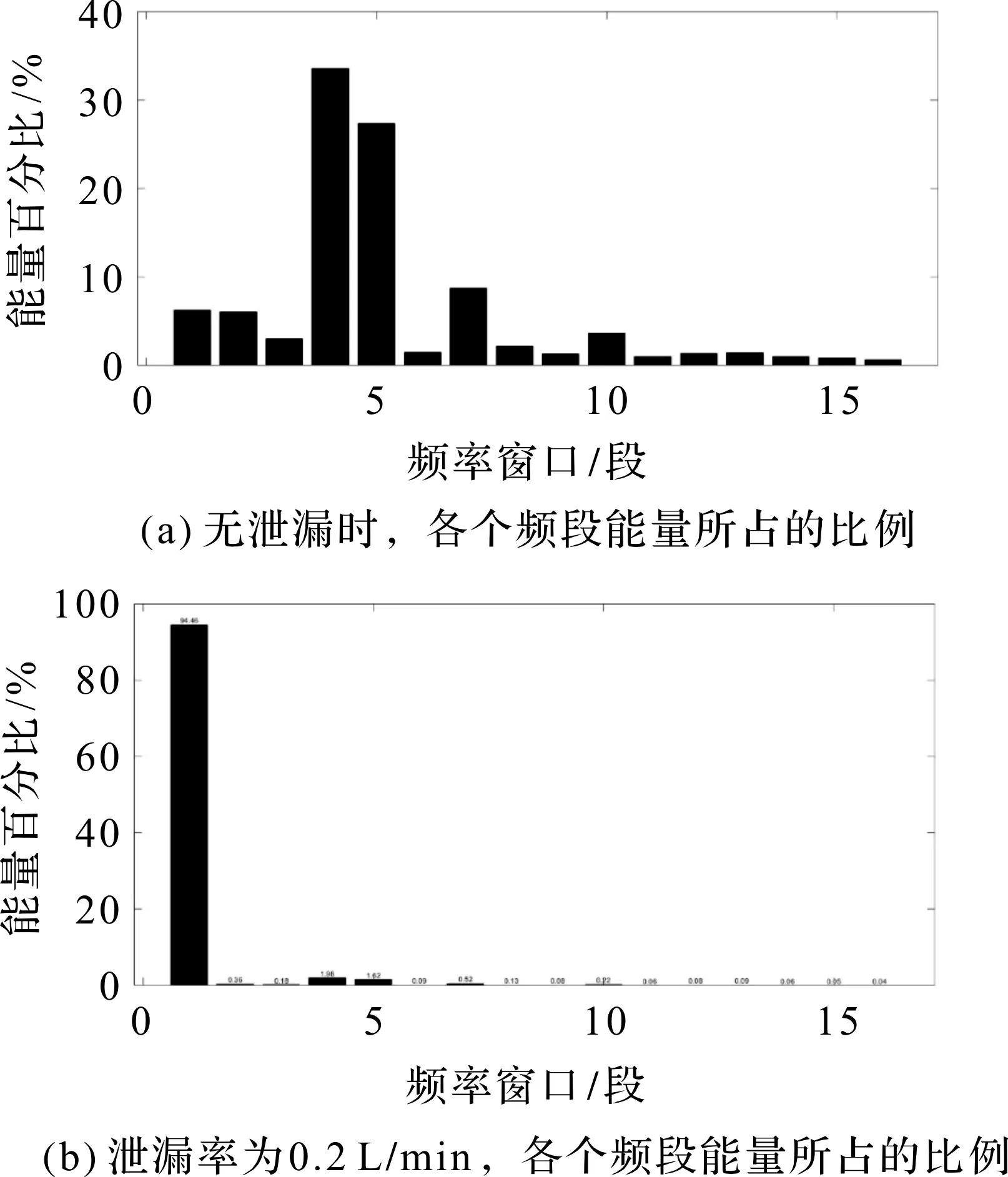
图6 各频段能量比较图Figure 6 Energy comparison chart of each frequency band

其后,利用阈值去噪法对信号进行处理。在确定声发射信号集中在0～18.75 kHz后,保留该频段的小波包节点系数,将其他频段噪声信号的小波包节点系数降为0,重构声发射信号。原始信号与降噪后信号频域对比如图7。经过小波包降噪,重构后信号滤除了声发射信号所在频段外,环境中其他频段的噪声,有利于之后对声发射信号的进一步处理。

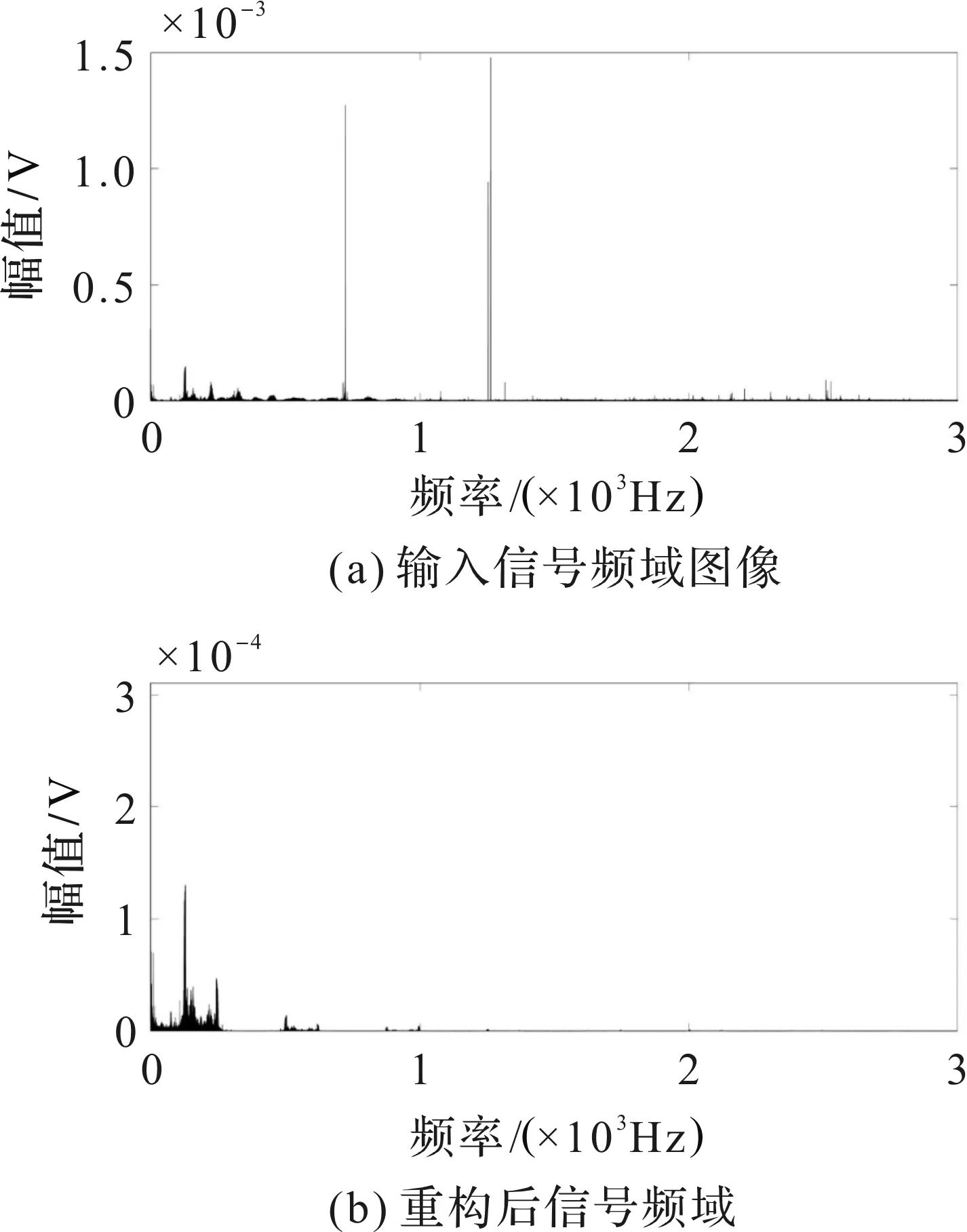
图7 重构前后信号频域图Figure 7 Signal frequency domain diagram before and after reconstruction

3 基于GRU的阀门内漏数据分析

在对声发射信号进行了降噪处理之后,分别使用支持向量机(SVM)、BP神经网络以及门控循环神经网络对降噪信号进行分类识别,比较不同模型对阀门内漏故障的识别效果。

3.1 基于支持向量机阀门内漏故障诊断模型

支持向量机是一种监督学习算法,在二元分类方面有很好的适用性[15]。为了降低误判率,本文采用了径向基函数(RBF)作为阀门内漏故障识别SVM模型的核函数,RBF核中有gamma和C两个参数,本文选择网格搜索的方法寻找各种可能的gamma和C,其后使用交叉验证的方法,确定精确度最高的参数[16]。

为了对阀门内漏进行准确识别,将阀门完好状态下的声发射信号分别和泄漏程度不同的多组阀门声发射信号进行组合,并作为数据集进行识别。每种泄漏率下,分别输入10组数据集,每组数据集约有300个采样点。将数据集以及其标签文件分别输入SVM模型中,每组随机选取其中200个样本作为训练集,余下作为测试集;求不同泄漏率测试集的准确率均值;评价不同泄漏率下的SVM模型故障识别准确性。表2为SVM模型阀门内漏检测的平均准确率,由表可知,随着泄漏率越小,SVM模型故障识别效果也在不断变差。在泄漏率低于0.8 L/min时,SVM模型识别准确率已低于85%。

表2 SVM模型阀门内漏检测平均准确率

3.2 基于BP神经网络阀门内漏故障诊断模型

BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络。它广泛应用于工业场合下的故障诊断中,将一个待定的输出向量与它的输入向量联系起来,实现模式识别[17]。

本文将不同泄漏率下的阀门声发射信号的特征值提取出来,将特征值作为BP神经网络的输入值,输出值则是阀门内漏速率。作为输入量的特征值包括压力、平均信号电平(ASL)以及有效值电压(RMS)。BP神经网络的输入端所输入特征量为3个,网络的输入节点数设置为3。根据本文需确定阀门泄漏率,所以输出节点应设置为7。考虑到隐层节点数过多会导致训练效率下降,再通过经验公式的推导与多次实验,确定最佳隐层节点数为7。那么诊断的网络结构可以确定为N(3,7,7)。

图8为BP神经网络的训练曲线,它表示的是训练过程中收敛精度的变化,由图可知在训练初期收敛精度下降较大,当迭代到100步时,曲线开始平缓,逐渐收敛,均方误差陷入局部极值无法跳出。

图8 BP神经网络的训练曲线Figure 8 Training curve of BP neural network

表3为不同工况下,阀门运行状态标签,表4为BP神经网络对测试集的部分输出和分类准确率。

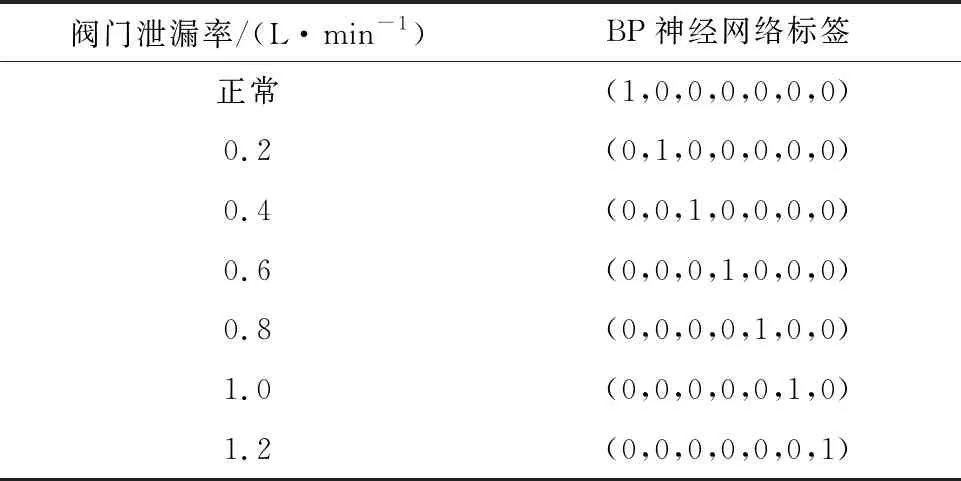
表3 不同工况下阀门运行状态标签

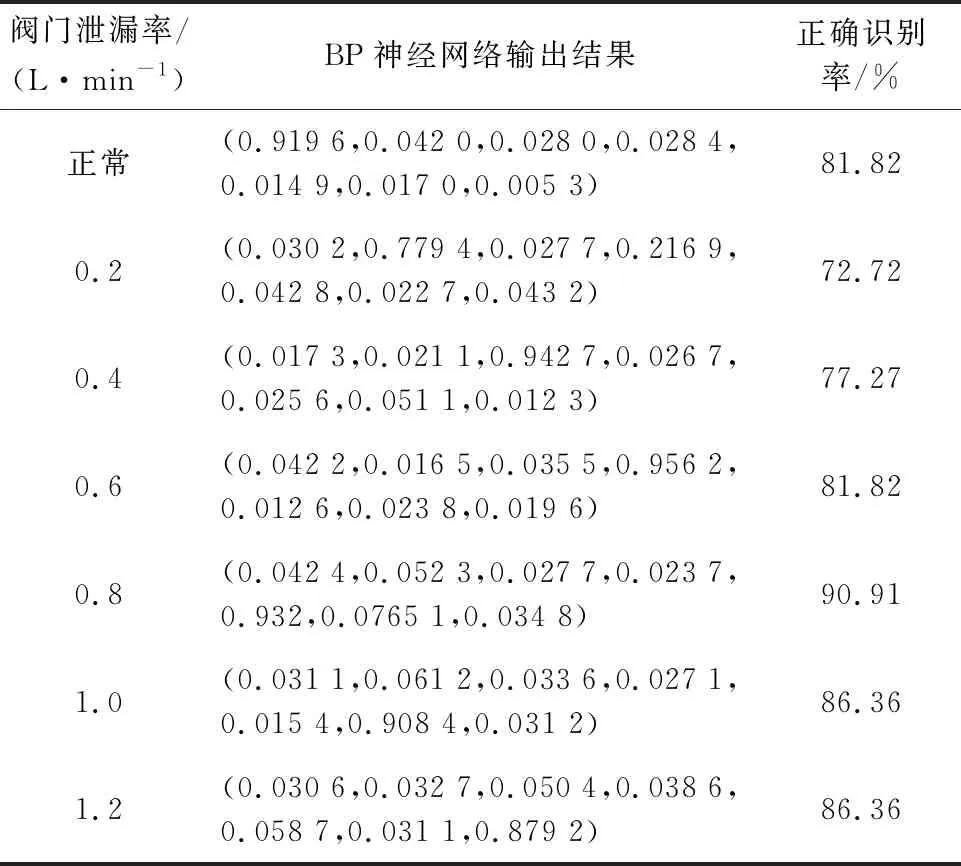
表4 BP神经网络对测试集的部分输出和分类准确率

由神经网络的训练结果和测试结果,可以看出BP神经网络算法训练后期陷入了局部极小值且迭代的花费的时间较长。测试结果中BP网络输出的精度不够高,正确识别的数量还有待提高。

3.3 基于GRU的阀门内漏故障诊断模型

利用未泄漏阀门的声发射数据对GRU模型进行训练;将未泄漏的声发射数据输入GRU模型;取预测数据与真实数据的差值,将差值由小到大排列,较小的99%的数据为可信数据,较大的1%的数据则不可信,99%为设定的置信率。

如图9,图中前10 000个数据是阀门尚未发生泄漏时采样所得的数据,后10 000个数据是阀门发生内漏时的采样数据。将它们与GRU网络输出的预测值数据进行比较,得到预测值与真实值的差值。将之前的99%置信率的数值作为基准,低于此值的为不可信数据,高于此值的为不可信数据,分别得到前后10 000个数据的置信率。

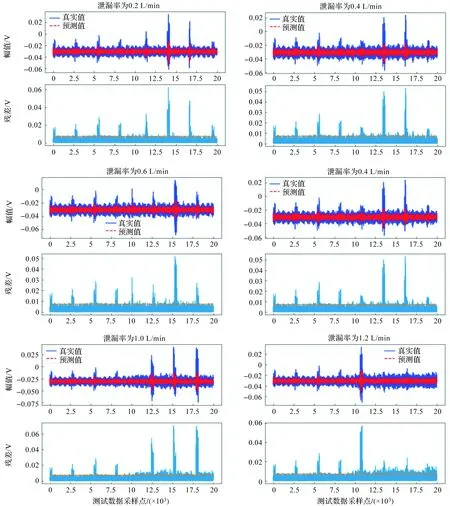
图9 阀门泄漏程度的GRU预测Figure 9 GRU prediction of valve leakage

如表5,取前1 000个正常声发射数据与后10 000个泄漏声发射数据置信率的差值。经过比对可以发现发生内漏时,置信率差值明显出现变化,随着泄漏率变大,置信率偏离程度也在不断变大。由置信率的偏离程度,可以判断阀门是否发生内漏。

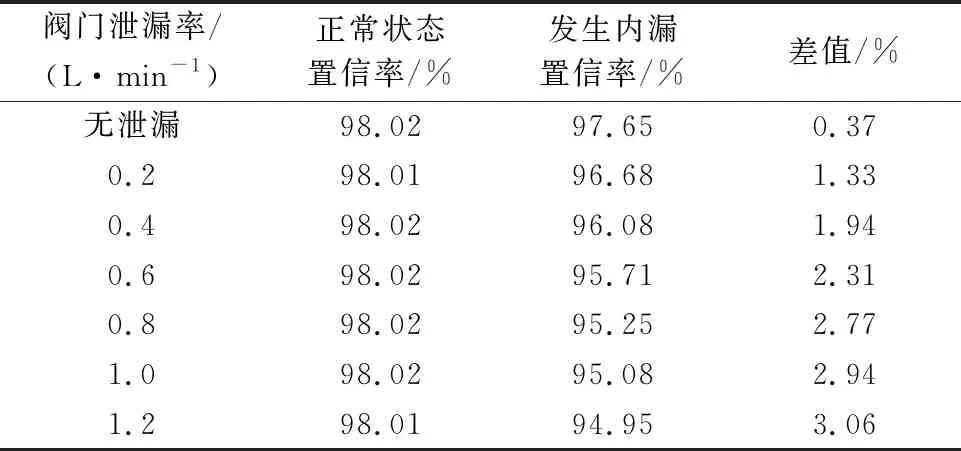
表5 压力为0.4 MPa时预测数据与真实数据置信率差值比较

在不同实验压力下对内漏程度不同的阀门进行实验,对所采集得到的数据进行进一步分析。如表6,可以发现在不同阀门压力下,当阀门发生泄漏时,其置信率差值变化明显,且随着泄漏的不断增大,差值逐渐变大。在不同的阀门压力下,仍可由置信率偏离程度判断阀门是否发生内漏。

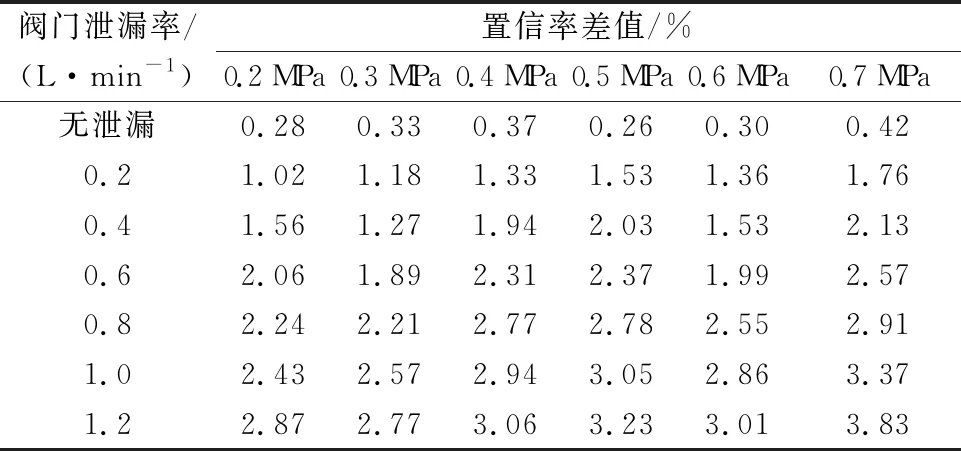
表6 不同压力下预测数据与真实数据置信率差值比较

当置信率差值大于1%时,可判断阀门发生泄漏,表7为GRU对测试集的分类准确率。比较表4BP神经网络对测试集的分类准确率,可知GRU在阀门内漏检测方面效果更好。

表7 GRU对测试集的分类准确率

比较支持向量机、BP神经网络和门控循环神经网络对阀门内漏声发射信号的处理效果如表8所示,可知门控循环神经网络利用时间序列对阀门故障进行判别的方法所取得的效果更佳。

表8 不同研究方法可测的最小泄漏量比较

4 结 论

阀门的内漏故障程度可以表征为阀门内漏时声发射信号的变化情况。给出一种基于门控循环神经网络的阀门内漏状态判别新方法。门控循环神经网络对于长时间序列数据十分敏感,并且能够保存长期记忆,以用于对短期记忆包含的信息进行校正。当发生泄漏后,声发射所接收数据的微小变化会与长期记忆所存储信息不同,因而造成与无泄漏工况下不同的差值,利用此差值可以判断泄漏率。在本文的实验工况下,门控循环神经网络的预测方法能够识别最小泄漏量为0.2 L/min的阀门内漏,其效果优于本文中实现的支持向量机以及BP神经网络预测方法。区别现有研究中所使用的检测方法,利用时间序列分析进行故障诊断的方法,使得检测效果有所提升,从而为阀门泄漏故障判断提供了一种新的方向。