例谈小学高年级几何解题策略

文∣邓玉玲

《义务教育数学课程标准(2011年版)》提到，“从现实生活或具体情境中抽象出数学问题，用数学符号建立方程不等式函数等表示数学问题中的数量关系和变化规律求出结果，并讨论结果的意义，这些内容的学习有助于学生初步形成模型思想，提高学习数学的兴趣和应用意识”。而模型思想要求将一个问题的解决拓展为一类问题的解决，因此合理运用模型的策略与方法的教学，有利于解决学生不能灵活解题的问题。本文重点解决在小学高年级的几何复习教学中如何通过图形表征、数学符号表征、转化等构等常用的策略与方法，帮助学生理解题目，促进学生形成举一反三、触类旁通的能力，使学习能力不同的学生在复习中均得到提高。

一、借助图形表征，培养学生建构意识

小学生的思维以具体形象为主，在解题过程中，借助直观图形有利于引导学生思维由形象过渡到抽象。在小学数学的“图形与几何”的教学目标中，提到培养学生关于空间观念、提高利用几何直观去进行思考的能力。所以，教师在教授几何知识的教学中，要合理引导学生建立直观图形，达到培养学生的空间意识，帮助学生快速掌握一些有效的分析解题方法，使其达到快速准确解题的目的，促进学生自觉构建图形的意识，提高学生灵活解题的能力。

(一)抓住关键词，构建图形，准确理解题意

复习时构建图形模型，把观察和思考联系起来，有利于培养学生的空间观念。

【例1】将一块棱长18厘米的正方体木料削成一个最大的圆柱体，求它的表面积、体积。

解题时要把第一句话中的关键词“削”“最大”用图形表示出来，如图1。“最大”的意思就是圆柱的底面直径等于正方体的棱长，圆柱的高等于正方体的高，用a=d=h表示,这样就很直观地表达了题目的含义，同时又帮助学生积累分析解决问题的经验，使学生解题的准确率和速度大为提高。

【例2】从一根圆柱体木料中锯出6厘米长的一段圆柱。剩下的木料是高与底面直径相等的圆柱体，表面积比原来减少了150.72平方厘米。原来圆柱体木料的表面积是多少平方厘米？体积是多少立方厘米？

抓住“锯”“剩下”“减少”等关键词画图发现少的150.72就是6C，6C=150.72，从而可求底面半径，此题可解。在平面几何方面，一个三角形和一个平行四边形等底等高，已知三角形的面积是35平方厘米，则平行四边形的面积是多少？根据第一句话隐含的意思构建图2。

观察图形, 得到在等底等高的平行四边形和三角形中,S平=2S三。

图1

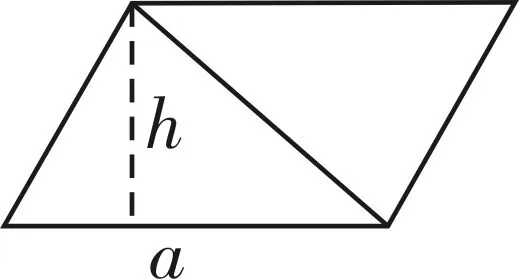
图2

从上面的例子可以总结出：抓住关键词、构建图形，能帮助学生准确快速地理解题意，提高解题的准确率和速度。

(二)借助技术展现动态图形，解读题目隐含的数量关系

信息技术可以打破时空的界限，展现图文并茂的特征，可以把学生难以理解的知识用动静结合的画面直观地呈现在学生的面前，清晰的表象，丰富了学生的思维，达到有效帮助学生理解题目含意的目的，找到题目隐含的等量关系。

【例3】一个棱长6.9厘米的正方体切成棱长2.3厘米的小正方体，可以得到多少个小正方体？ 小正方体的表面积之和比原来大正方体的表面积增加了多少？

图3

根据题目的描述进行构图，如图3。

从图3可以看到长可分3块，宽也可分3块，因此一层有3×3=9 ( 块)，高分3层，因此一共可切到3×3×3=27(块)。当教师在课堂上讲解到表面积之和增加多少时，用动画演示使学生清晰地看到：每切下一刀就会多了两个边长为6.9厘米的正方形截面，切6刀增加了12个截面，故得：6.9×6.9×12=571.32(平方厘米)。

完成这题后，教师把棱长改为12厘米，再做演示，然后引导学生对比，得出结论：一个棱长为M的正方体可以切成棱长为N的小正方体的块数是(M÷N)的3次方(M可以被N整除)。

【例4】一个长方体水池，底面为边长51厘米的正方形，里面插着一根长1.1米的木桩，木桩的底面是一个棱长是5.3厘米的正方形，木桩有一部分浸在水中，一部分露出水面。现将木桩提高21厘米(仍有部分浸在水里)，那么露出水面的木桩浸湿部分面积为多少平方厘米？

教师在课件中先出示木桩插在水里的图(如图4)，再点击出示木桩提起水下降的动画画面，让学生清楚看到湿的部分包含两个部分，一部分是木桩提起露出的21厘米，另一部分就是木桩提起后水下降露出来的部分，如图5。完成此题后引导学生得到此类题的数量关系：从水里提起或放入水里时浸湿部分的面积=提起或浸入的浸湿的面积+因为水面下降或上升造成的浸湿面积。

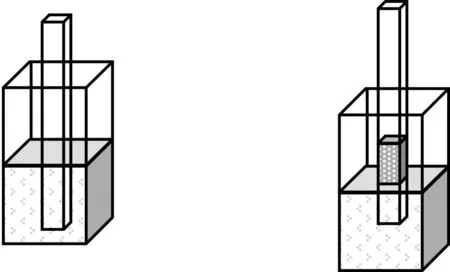
图4 图5

利用技术动态构图可以有效突破解题的难点，有效提高学生的解题能力。

二、借助数学符号表征，培养学生抽象意识

六年级学生已具有一定抽象能力，具备学习抽象符号模型的基础。数形结合和符号化是小学数学的重要数学思想，2011年版课标指出“符号感主要表现在：能从具体情境中抽象出数量关系和变化规律并用符号来表示，理解符号所表达的数量关系和变化规律会进行符号间的转换”。在“几何复习”教学中，教师引导学生从重点词句入手，构建图形，使文字直观化，把直观看到的结果用数量关系或字母符号表示出来，使问题迅速得到解决。

(一)从重点词入手，用符号表示数量关系

重点词是指在小学数学解决问题中，与题目的解题方法相关或隐含等量关系的词语。

【例5】把一块棱长10厘米的正方体铁块熔铸成一个底面直径是20厘米的圆锥形铁块。这个圆锥形铁块的高约是多少？(得数保留整厘米数)

(二)从重点词入手构建图形，挖掘隐含的数量关系

有些题目表面看比较复杂，如果从重点词入手构建图形，就能直观看到隐含的数量关系。

【例6】一个长方体，如果长增加1.5分米，则体积增加3立方分米；如果宽增加2.3分米，则体积增加11.5立方分米；如果高增加2.4分米，则体积增加9.6立方分米。求这个长方体的表面积。

引导学生抓住重点词语“长增加”“宽增加”“高增加”构建出图6。通过观察，找到隐含的数量关系，并用符号表示。

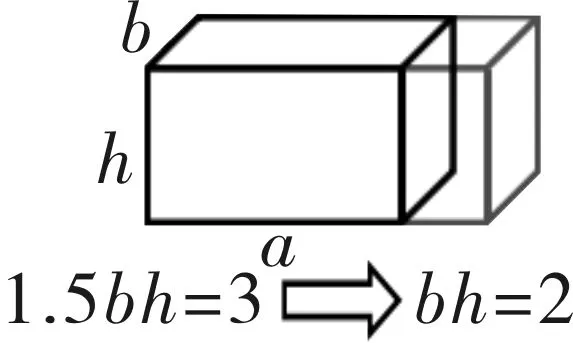
图6

因此，在几何解决问题复习教学中，教师引导学生从重点词入手构建图形，抽象出数量关系和变化规律并用符号来表示，有效提高学生构建知识的意识和能力，同时不同的题目可以用相同的数量关系列算式或列方程来解，培养学生“以不变的方法应万变题目”的意识和能力。

三、借助转化，提高学生综合运用知识的能力

(一)构造特殊图形，化难为易

特殊与一般思想是一个非常重要的数学思想方法。特殊与一般可以互相转化，对于难以求解的一般问题，也可以转化为特殊问题，发现解决问题的途径，从而解决一般问题。有些几何题对于某个年级的小学生来说比较难理解，可以通过由已知条件构造出一个特殊的图形，降低难度破解题目。

图7

【例7】长方形ABCD的面积是24平方厘米，P为长方形内的一点，如图7，求阴影部分的面积是长方形面积的( )。

图8

这道题对于四年级的学生比较难理解，对于六年级的学生虽然可以代入字母求解，但过程比较烦琐，原因是P为长方形内任意一点解题难度较大，而任意一点即包括在长方形中心的那点，因此中心点的规律也符合任意一点的规律，于是构建出图8,观察图8得到：S阴影=S长÷2，此题迎刃而解。

(二)从已知的相关知识入手，化未知为已知

六年级的几何复习包括了整个小学阶段的几何知识，知识点多而散，有些知识学习时间间隔较长回忆起来有些困难，学生甚至已经忘记部分知识。学生需要将题目问题转化成已掌握的相关知识来解决，以此提高学生的综合解题能力和综合学习能力，所以在复习教学中教师注意引导学生利用转化的方法，重建模型。

总之，在几何解决问题复习中有效利用图形表征、数学符号表征、转化等构等常用的策略与方法教学，既避免学生生硬套题，又培养学生主动构建的意识和空间想象能力，有效地促进学生综合解题能力和综合学习能力的发展。