激光等离子体尾波中的太赫兹阻尼辐射

杨林森，周素云

(江西科技师范大学材料与机电学院，江西 南昌 330013)

太赫兹(THz)辐射，其波段介于0.1 THz(1 THz=1012Hz)的亚毫米波与10THz的远红外线之间，应用涉及物理、化学、生物、材料科学等边缘科学[1,2]，例如，THz光谱分析实现对分子的识别,THz波对物质的无损检测。1993年，Hamster等人[3]在研究激光等离子体尾波加速电子时就预言了激光等离子体相互作用能够激发THz辐射，并首次在实验中观察到4.6THz的电磁脉冲。理论上预测这种新型辐射源可提供功率高达MW量级、场强为MV/cm的THz脉冲。基于激光等离子体相互作用的THz辐射源具有不存在材料损伤阈值、能量转化效率高等优点，是目前的一个研究热点。

当激光在稀薄等离子体中传播时，能够激发等离子体波，也称为尾波。选择合适的激光脉宽和等离子体密度，激光能够在等离子体中共振激发THz振荡电流，振荡电流向空间辐射THz波。由于尾波中振荡电流的对称性，总的净电流非常小，相应的辐射强度就很低。各种基于提高尾波THz净电流强度的机制被提出，主要有渡越辐射[4]、磁化等离子体中的Cherenkov辐射[5]和非均匀等离子体中的线性模式转换[6-7]、用基频和倍频激光合成的双色激光激发THz辐射机制[8]。这些理论和实验研究主要是关于径向辐射或者斜向辐射的，但是这种辐射的聚焦准直性较差，在远距离传播时难以对准目标。后来Amico等人[9]发现激光在空气中成丝辐射的THz波主要在向前方向，即纵向方向，其纵向辐射强度比径向方向高出两个数量级，THz辐射波主要分布在激光轴的圆锥内，偏振方向在径向。这种纵向传播辐射聚焦准直性较好，很容易定位远距离目标，甚至数千米远，但是其激发机制和增强方式还不明确，存在争议[10]，需要进一步研究。本文基于激光在稀薄等离子体中激发尾波解析模型，进一步考虑电子阻尼振荡，研究了等离子体尾波中的纵向传播THz辐射，调查了太赫兹辐射的空间分布，以及等离子体层厚度的影响。

1 模型与公式

考虑一束高斯激光脉冲在稀薄等离子体中传播，激光包络场矢势为：

(1)

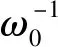
图1 激光穿过等离子体层后尾波振荡激发THz辐射示意图

∂tp0=∇(φ0-γ0)-νp0

(2)

其中

(3)

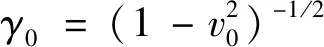
(4)

∂t(∇φ0)=-neu0

(5)

其中ne,n0分别是临界密度nc归一化的电子密度、离子密度，Z是离子电荷数，u0是光速归一化的电子流体速度。基于轴对称圆柱坐标系，由(2)-(4)可得：

(6)

ne=∂ηηφ0+(4φ0/b2)(ρ2/b2-1)+Zn0

(7)

(8)

通过解方程(6)-(8)可以得到电流密度：

jz=n0u0z=∂ηηφ0

(9)

jρ=n0u0ρ=∂ηρφ0

(10)

其中jz和jρ是纵向电流密度和径向电流密度。

如果激光强度较弱(a0<1)，等离子体中电子振动是非相对论的，电子振荡的辐射波频率等于等离子体频率。按照经典辐射理论，每单位立体角的辐射能量为：

(11)

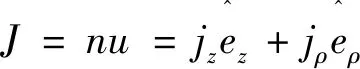
(12)

其中θ是观察方向与激光传播方向的夹角。

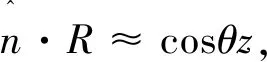
(13)

2 尾波中振荡电流辐射的纵向传播THz波

(14)

其中νp,ν0,λ0和λp分别是等离子体频率或者辐射频率，激光频率，激光波长和等离子体波长。选择合适的等离子体密度，就能得到THz辐射波。例如，对于波长为λ0=1 μm的激光，要得到频率为ν0=3×1012Hz的辐射波，用(14)式计算得到等离子体密度n0=10-4和等离子体波长λp=100λ0。在非相对论情况下，激光波长约为等离子波长一半时，激光等离子体共振产生，尾波最强，因此选择激光脉宽L=50λ0。基于方程(6)-(13)可得到尾流场的电子密度分布，标势分布，径向电流分布和纵向电流分布。

图2(a)和2(b)分别是激光强度为a0=0.5和a0=2激发的尾波中在ρ-η面上的二维电子密度分布图，其余参数为b=50λ，L=50λ0，n0=10-4,ν=0.000 1。η=0处是激光所在位置，第一个空泡包含激光场在内，所以其尺度比其他空泡要更大。可以看出图2(a)是典型的线性尾波结构，电子空泡与电子峰的尺度基本一致，其中蓝色部分是电子缺失位置，即电子空泡，红色部分是电子密集处或电子峰。图2(b)中电子空泡尺度大于电子峰，出现尖锐的电子峰，表现为非线性结构。在线性尾波中，静电场表现为正弦分布，由于等离子体碰撞，尾波场是逐渐衰减的，衰减速度由阻尼系数决定，如图3，其参数为a0=0.5，b=20λ，L=50λ0，n0=10-4。如果定义衰减长度为空泡中标势衰减为第一个空泡最大标势的1/e时的距离，对于ν=0.000 1，衰减长度为3 000λ。

η/λ

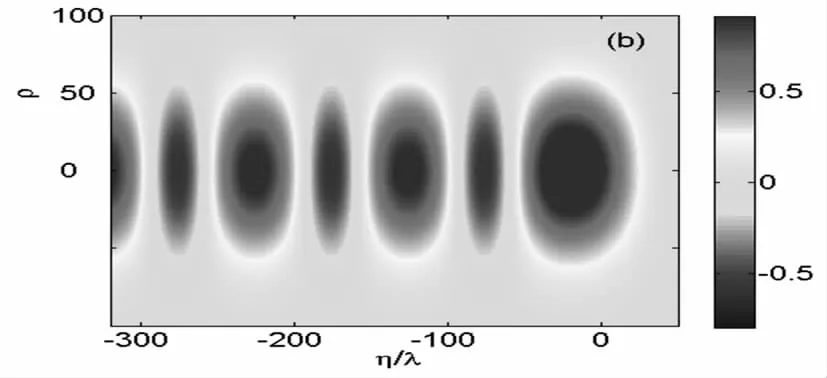
η/λ图2 尾波中电子密度分布(a)a0=0.5(b)a0=2

激光等离子体共振时激发的尾波幅度最大，即使在激光穿过等离子体层后，尾波振荡仍然能维持较长时间。在轴对称的运动坐标系中，尾波中的电流可以分成纵向振荡电流jz和径向振荡电流jρ两个分量。图4(a)和4(b)分别是尾波中径向和纵向振荡电流密度的二维分布图，参数与图3一致。

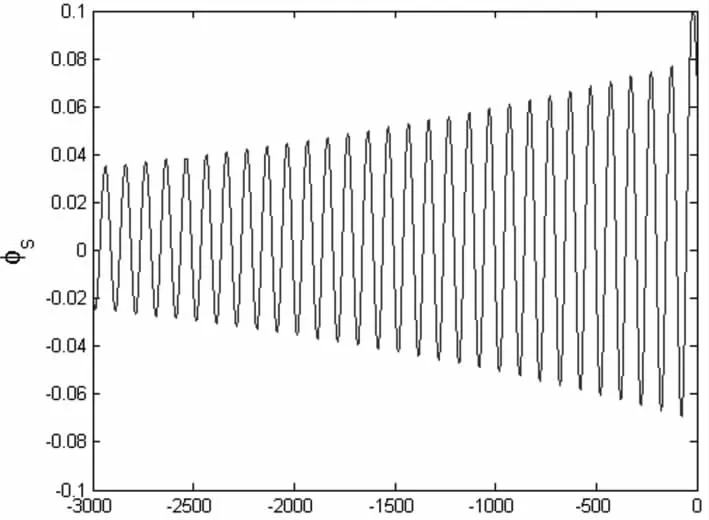
η/λ图3 激光轴上的标势φs分布

η/λ

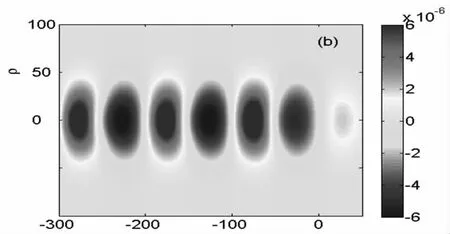
η/λ图4 (a)径向电流密度分布jρ(b)纵向电流密度分布jz

在图4(a)中，径向电流消失在激光轴，随着半径ρ的增加，电流渐渐增大，在空泡的边缘达到最大。图中红色与蓝色部分代表相反的电流方向，可以看出，以激光轴对称的径向电流方向是相反的，并且同一个空泡或者电子峰前端与后端的电流方向相反。由于η=z-t，与空间位置和时间都有关系，尾波中任意一点的径向电流都是以激光轴为中心沿径向振荡。纵向振荡电流分布与径向电流分布不同，其峰值在激光轴上，并且在同一个空泡或者电子峰中，其前端与后端处的电流方向相反。

由于纵向传播的THz辐射主要来自径向振荡电流，根据图4(a)中的径向电流密度分布，基于方程(13)，可以计算在不同观察点所得到的辐射强度，并且可以计算激光穿过不同厚度等离子体层产生的辐射分布。图5是径向振荡电流辐射的THz波角分布，即单位立体角辐射功率dP/dθ随角度θ的变化曲线，参数与图3一致。其中蓝色实线是激光在1 cm厚度的等离子体层产生的辐射，红色虚线是在1 mm的等离子体层产生的辐射。对于1 mm厚度等离子体层，其辐射范围大约在0°～20°立体角内，在0°～10°内基本均匀分布，然后迅速下降。而在1 cm厚度等离子体层，辐射主要集中在0°～11°内，半宽角度为5°，并且辐射功率峰值不在激光轴方向，在偏离轴8°位置，在10°后辐射强度快速衰减。

θ/(°)图5 径向振荡电流产生的单位立体角THz辐射功率dp/dθ与辐射角度θ的关系

由于坐标零点选取在等离子体层的中心，太赫兹辐射呈现为圆锥体分布，圆锥辐射的立体角随着等离子体层厚度的增加而减小，其辐射强度与等离子体厚度有关系。对(13)式进行角度积分，可得到不同厚度等离子体层的单位立体角THz波辐射功率，图6是单位立体角辐射功率与等离子体厚度d的关系曲线，参数与图3一致。可以看出辐射功率随等离子体厚度是单调非线性增加的。

d/mm图6 THz辐射功率与等离子体层厚度d的关系

3 结论

基于二维等离子体尾波解析模型，计算了激光在等离子体中共振激发的线性尾波阻尼辐射THz波。分析表明，纵向传播THz辐射主要来自尾波中径向振荡电流，由于径向振荡电流峰值在尾波空泡边缘，消失在激光轴，使得其辐射的THz波强度峰值偏离激光轴一个小角度，集中在以激光轴为中心的小角度圆锥范围内。等离子体层厚度对径向太赫兹辐射的空间分布和功率影响比较大，在设计THz辐射实验中应充分考虑这些因素。