非线性薛定谔方程的精确解析解

赵 欢

(南昌理工学院， 江西 南昌 330044)

自从理论上首次提出孤子并在实验中得到证明以来[1]，孤子的研究已成为一个有吸引力的研究领域。孤子作为一种超短脉冲的特殊形式，能够保持其速度和形状不变。 在长距离传输中，由于其在组速度色散(GVD)和非线性(例如自相位调制，SPM)效应之间的平衡而引起的[2]。 实际上，已经在一些领域研究了孤子，包括应用数学，理论物理学，玻色-爱因斯坦凝聚和非线性光学，以及由于其优越的性能而在超快光学中的某些物理应用[3]。

在本文中，我们将介绍一个描述具有非线性和分布色散的非均匀光纤中孤子传输的动力学的广义非线性薛定谔方程[4]

iut+id(t)u+b(t)uxx+l(t)u|u|2=0

(1)

其中u=u(x,t)。对于方程(1)，文献[5]通过特殊函数的选择研究了孤子的相互作用。文献[6]通过Hirota方法获得了单孤子和双孤子解。文献[7]构造了圆柱非线性薛定谔方程并给出了四个特殊变换。文献[8]通过Darboux变换和Lax对得到了孤子解。文献[4]讨论了方程(1)类Dromion孤子相互作用。在空间/实验室等离子体、流体力学和光纤中，方程(1)有很多重要的特例，比如圆柱和球面几何修正的尘埃声波包络孤立波非线性薛定谔模型、变/分布系数广义非线性薛定谔模型以及某些非均匀光纤非线性薛定谔模型等等[7]。

假设

u(x,t)=eiφ(x,t)Δ[ω(x,t)]

(2)

其中ω(x,t)=τ3(t)+xτ4(t)。此时，方程(1)变为

(3)

且

(4)

其中σ1和σ2是积分常数，τ1(t)和τ2(t)是积分函数。

1 亮暗孤子解

非线性薛定谔方程的亮孤子和暗孤子解是近年来研究的热点[9]。亮孤子描述了在调制不稳定性下，恒定振幅波产生的脉冲。暗孤子代表调制稳定的恒幅波的脉冲。为了获得这两种解，我们有

Δ[ω(x,t)]=δ1Sech[ω(x,t)]+

δ2Tanh[ω(x,t)]

(5)

将 (5)代入(3)可得如下两种解

(Ⅰ)、

(6)

其中σ3和σ4都是积分常数。此时可得方程(1)的亮孤子解

u(x,t)=

xτ4(t)]δ1

(7)

在方程(7)中令

σ1=σ2=σ3=σ4=1,δ1=2

亮孤子解(7)的物理结构见图1。

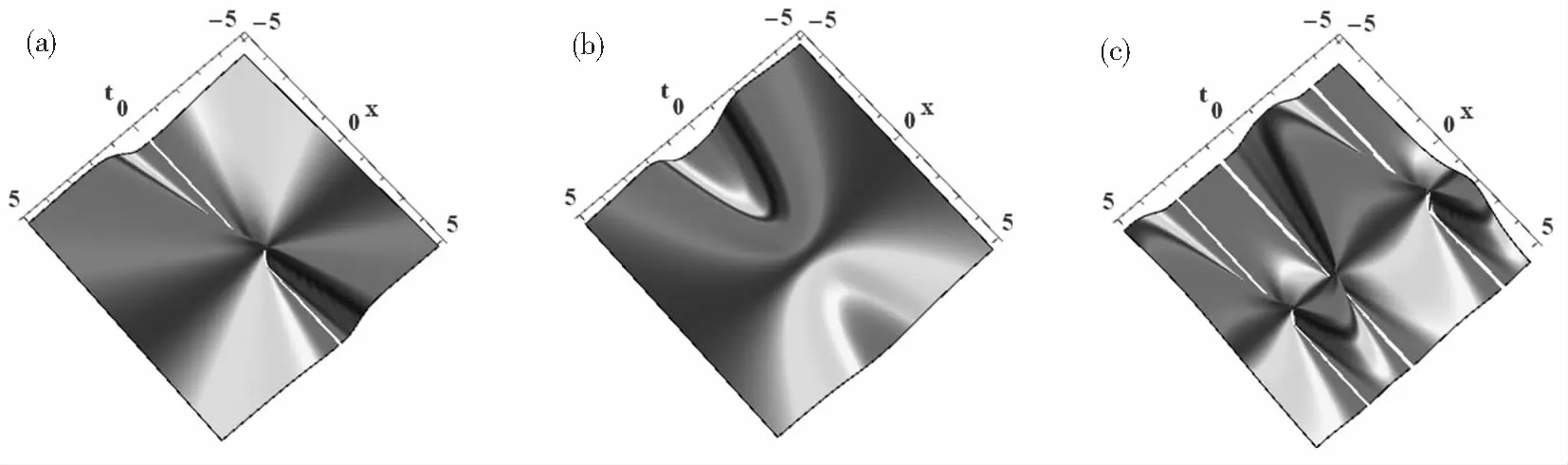
图1 (a) b(t)=-1;(b) b(t)=-t;(c) b(t)=cost

(Ⅱ)、

(8)

此时可得方程(1)的暗孤子解

(9)

在方程(9)中令

σ1=σ2=σ3=σ4=1,δ2=2

暗孤子解(9)的物理结构见图2。

图2 (a) b(t)=-1;(b) b(t)=-t;(c) b(t)=cost

2 双曲函数解和三角函数解

为了获得方程(1)的双曲函数解和三角函数解[10-11]，我们假设

(5)

其中

G″[ω]=-JG′[ω]-KG[ω]

(6)

G′[ω]/G[ω]满足：

(7)

(8)

(9)

其中ϑ=J2-4K。将方程(5)-(9)代入(3)中可得方程(1)的双曲函数解和三角函数解如下：

(Ⅰ)、

(10)

(11)

(12)

其中

(Ⅱ)、

(13)

(14)

(15)

其中

(Ⅲ)、

(16)

(17)

(18)

其中

8Kτ4(t)2]/[4τ4(t)2]

为了了解双曲函数解和三角函数解的特点，我们选择解(16)和(17)作为例子，假设

σ1=σ2=σ3=σ4=C1=1,C2=-2,η1(t)=2

此时他们的物理结构被展示在图3和图4中。

图3 K=-1,(a) b(t)=-1;(b) b(t)=-t;(c) b(t)=cost

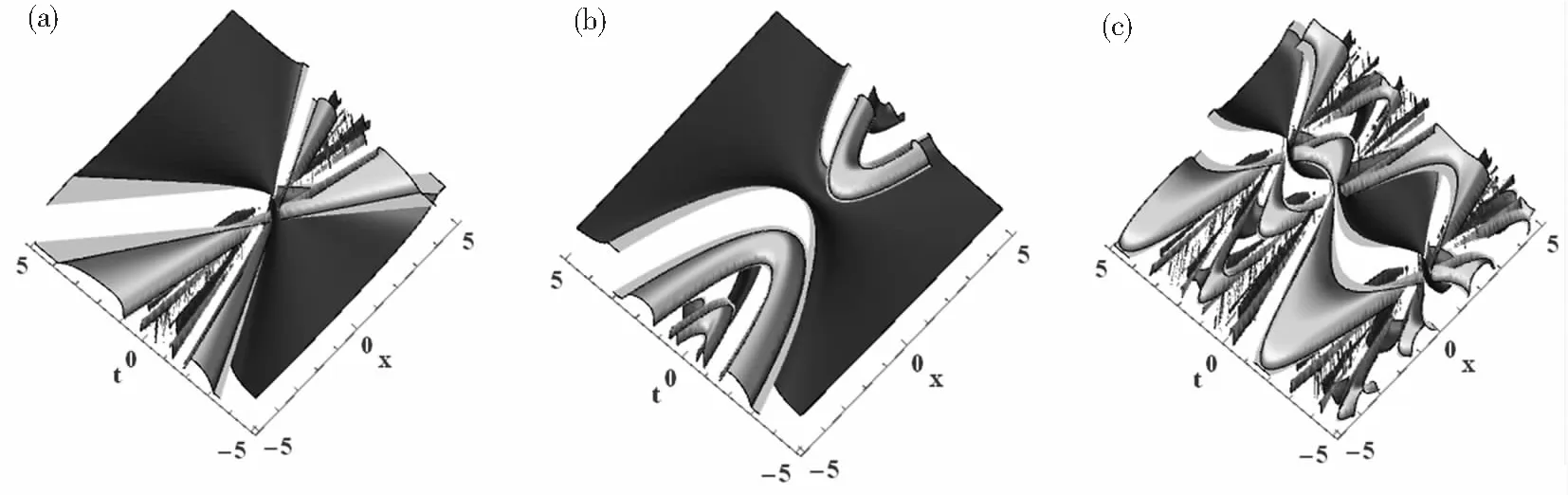
图4 K=1,(a) b(t)=-1;(b) b(t)=-t;(c) b(t)=cost

3 结论

本文获得了变系数非线性薛定谔方程大量的精确解，其中包含了亮孤子解、暗孤子解、双曲函数解、三角函数解以及一部分有理函数解。这些解的物理结构被展示在图1～图4。所有的解都通过Mathematica软件验证是正确的。