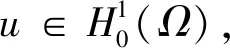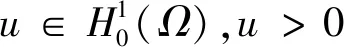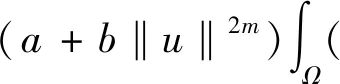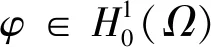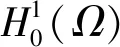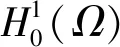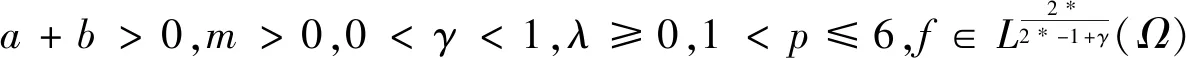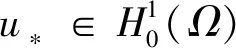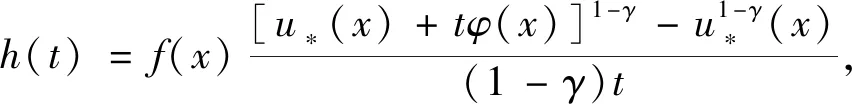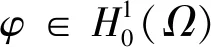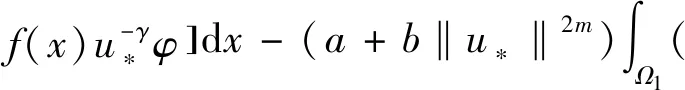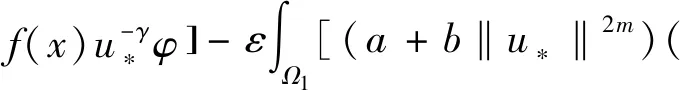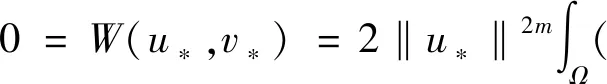一类带奇异项的非局部问题正解的唯一性

林荣瑞，佘连兵*，吴莲发

(1.六盘水师范学院数学与计算机科学学院，贵州 六盘水 553004；2.上饶师范学院数学与计算机科学学院，江西 南昌 334001)

考虑如下带非局部项的奇异椭圆问题

其中Ω⊂N(N≥3)是一个有界开区域且具有光滑边界∂Ω,a,b≥0且a+b>0,m>0，λ≥0,1

当m=1时，文献[1]率先研究了问题(1):

利用变分方法和一些分析技巧，获得了上述奇异非局部问题正解的存在唯一性。文献[2]研究如下非局部问题,

在文献[1]和[2]的启发下，本文利用变分方法和临界点理论，证得了问题(1)正解的存在唯一性，推广了文献[1]和[2]中的结果。

(2)

记S为

(3)

最佳Sobolev常数。

证明首先，证明m*有定义。由Hölder不等式和(3)式，可得

(4)

(5)

从而，根据(4)式和(5)式，可得

(6)

令ωn=un-u*，只需证明当n→∞时‖ωn‖→0。根据Vitali定理，可以断言

(7)

根据(4)式，我们有

进一步，由(6)式和Brezis-Lieb引理，可得

(8)

一方面，1

这就意味着I(u*)=m*。另一方面，p=2*时，依据(6)-(8)式以及范数的弱下半连续性，可得

这就得到I(u*)=m*。引理1证毕。

下面，给出本文的主要结果及证明。

(9)

根据Lebesgue控制收敛定理，可得

(10)

对任意的x∈Ω,记

h′(t)=f(x)

这就意味着:h(t)对一切的t>0是非增的。进一步，对任意的x∈Ω，有

其中当u*(x)=0且φ(x)>0时，上式值可能是+∞。从而，根据单调收敛定理(Beppo-Levi定理)，可得

这里可能取到+∞。在(9)式中让t→0+，由(10)式可得

(11)

这就意味着u*(x)>0在Ω中几乎处处成立。

(12)

(u*+εφ)+=max{u*+εφ,0}

显然，Ψ≥0。在(11)式中取φ=Ψ，记Ω1={x∈Ω:u*+εφ≤0}，结合(12)式，可得

当ε→0+,有measΩ1→0,上式两边同时除以ε并令ε→0+,可得

因此，这个不等式对于-φ也成立。故,u*是问题(1)的一个正解且I(u*)<0。

最后，问题(1)解的唯一性。假设ν*为问题(1)的另一个解。由(2)式，可得

(13)

(14)

根据(13)式和(14)式，可得

(15)

其中

由Hölder不等式，可得

由0<γ<1,p>1，易得到如下两个不等式

(r-γ-s-γ)(r-s)≤0,(rp-1-sp-1)(r-s)≥0,∀r、s>0

因此

一方面，若a>0，由(15)式，推得a‖u*-ν*‖2≤0。这就意味着:‖u*-ν*‖2=0,即u*=ν*。另一方面，若a=0，由(15)，推得‖u*‖=‖ν*‖且W(u*,ν*)=0。从而，有

即u*=ν*。因此u*是问题(1)的唯一解。定理1证毕。