固体火箭发动机装药设计的一种燃面推移方法研究 ①

2021-07-15刘登航卓长飞

固体火箭技术 2021年3期

王栋，刘登航，卓长飞

(南京理工大学机械工程学院，南京 210094)

0 引言

燃面变化规律是固体火箭发动机装药设计的一个核心问题，直接决定着发动机推力曲线走向[1-2]。目前已有的燃面推移计算方法包括解析法、作图法、通用坐标法、实体造型法、网格法、level-set法、最小距离函数法等。其中，解析法、作图法与通用坐标法存在对三维复杂药型计算困难的局限性[1-6]。实体造型法可利用大型通用CAD软件，但不易实现与流场耦合计算，对于不同药型需要进行不同的推移构造和几何尺寸定义，不具有通用性[7-13]。网格法通用性好，但对复杂装药在推移过程中出现部分型面的交汇、分离和变形的情况时误差较大[14-19]。level-set法不需要显式的追踪活动界面，易于处理复杂界面及其在移动过程中发生的拓扑变形，但对不同药型的初始型面，需要手工给出，或者需要将初始型面用非结构网格离散输入，装药初始型面设置过程非常复杂[20-28]。最小距离函数法具有较强的通用性，但计算过程复杂，计算速度偏慢[29-35]。

目前，基于CAD软件的燃面算法多只是计算燃面变化规律，少有与一维内弹道相结合揭示整个燃烧过程内流场变化情况的。本文采用离散网格思想，针对任意型面非槽平端的单通道装药或者实心装药，研究一种通用的燃面推移计算方法，该计算方法与一维内弹道相结合，其优点在于操作简单，计算量小，基于C++编写的控制台程序计算速度快，具有良好的通用性，可以计算多种非槽的单通道装药或者实心装药，能够较为准确捕捉燃面拓扑结构变化，可得到装药在燃烧过程中的一维内流场参数变化情况，与装药实际燃烧过程吻合度较高，对于固体火箭发动机设计具有良好的辅助预示效果。

1 装药初始表面数据获取

1.1 装药建模

利用NX 12.0软件的二次开发工具Block UI Styler模块以及SNAP编程接口，编写参数驱动的装药设计程序。该程序对于常见的非槽平端单通道装药或者实心装药给出参数驱动的建模方式，包括端面为平面的星孔装药、车轮孔装药、锥柱孔装药、梅花装药、圆柱孔装药、多臂形装药、十字型装药等；对于用户自定义的非槽平端单通道装药或者实心装药模型也给出了模型导入接口，如图1所示。

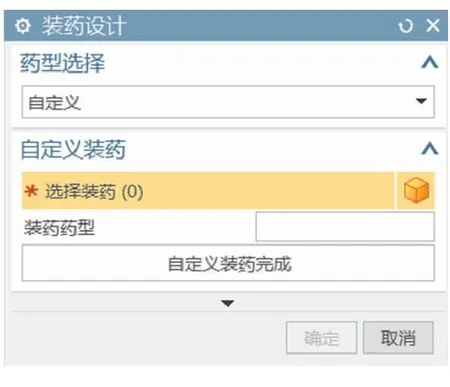
图1 自定义装药模型导入界面

对于常见装药，用户只需要给出参数，程序就可以自动建立三维模型。例如，要建立如图2所示的车轮孔装药模型，在图3所示的常见装药生成模型界面中选择“车轮孔”，并输入尺寸轮臂数5、装药外直径40 mm、特征长度10 mm、装药长度500 mm、轮边夹角70°、角分数0.55、轮臂高度4 mm以及3个过渡圆半径均为0.5 mm。

图2 车轮孔装药模型

图3 常见装药模型生成界面

1.2 表面离散

进行装药表面离散是为了获取初始表面数据。离散点越密集，越能够反映药真实物理形状。本文的离散方法是在前人已有的射线旋转相交法[18-19]的基础上改进得到的射线摇摆旋转相交法。射线旋转相交法是从装药轴线上引出一条射线，与装药的内外表面相交求离散点，射线旋转一周得到在该轴线位置处的一圈装药离散点，然后挪动射线到轴线上的下一位置，继续旋转求交，直到离散完整个装药内外表面。新方法射线摇摆旋转相交法增加了相交射线的摇摆回旋操作，使其能够处理装药离散面与射线有多个交点的情况。

参数设置如图4所示，参数M用于将装药沿轴线均匀划分为射线旋转截面，参数N决定射线在截面处每一次旋转的角度。

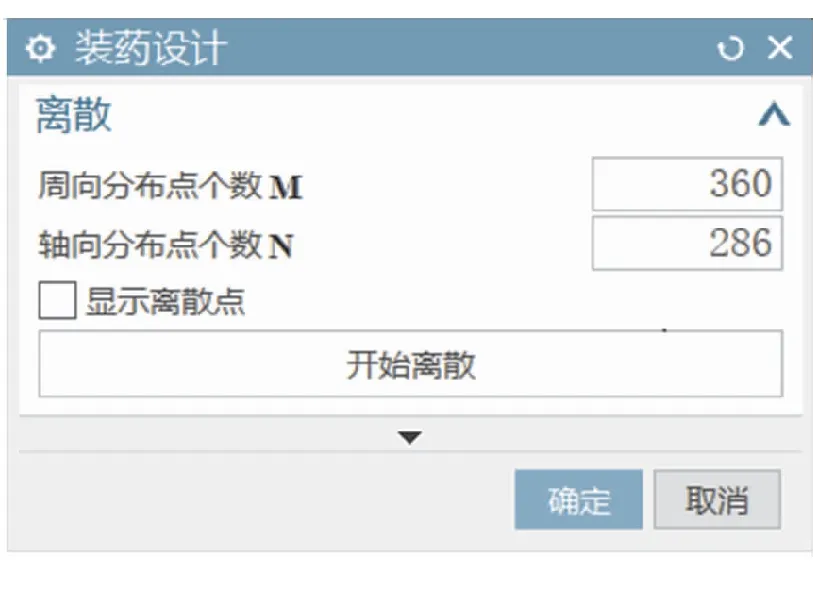
图4 装药面离散参数输入界面

以车轮孔装药内表面的离散为例进行说明，图5所示为车轮孔装药在轴向某一截面的内表面轮廓。前人所使用的旋转相交法在这种情况下射线直接逆时针从位置1经过位置2、3直接旋转到位置4，无法处理中间有多个交点的情况；改进后的摇摆旋转相交法令射线逆时针顺时针交替旋转，在位置1和4之间按照A-C-B-D-F-H-E-G的曲线顺序摇摆求相交点。然后，在轴向下一截面位置处的内表面上继续摇摆旋转求相交点，直到摇摆旋转相交完整个车轮孔装药内表面，得到该面上所有的离散点。

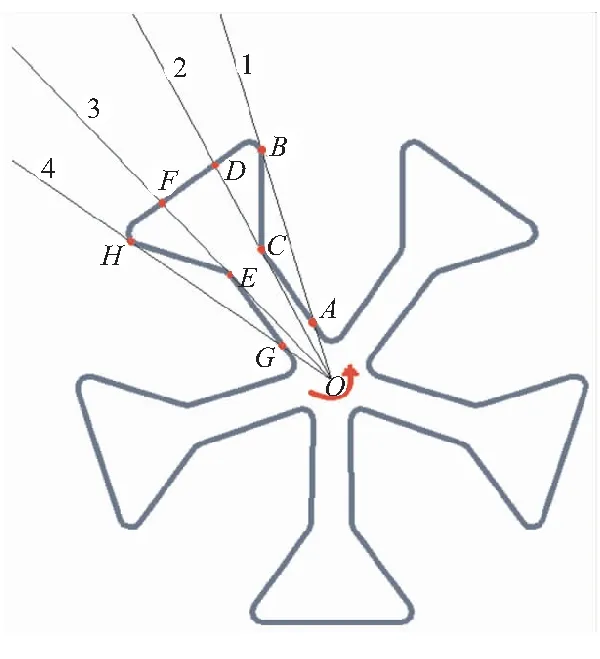
图5 车轮孔装药内表面离散截面轮廓图

对装药端面进行离散时，将端面看成是特殊的轴向截面，可用射线摇摆旋转相交法求出端面的边界离散点，再通过简单的插值方法插入端面的非边界点。示例车轮孔装药最终离散结果如图6所示。

图6 车轮孔装药离散结果

1.3 数据结构

为便于管理离散点数据，采用链表作为基本数据结构。装药侧面上的一行链表点节是由包络一圈的离散点集构成的，端面上的一行链表则是同一射线上的离散点集构成的。整个装药的数据结构如图7所示，将一个面上的所有链表按一定顺序编织成网格，再将装药的每个面作为节点串成一行面链表，所有面的网格组合起来就是整个装药的网格。

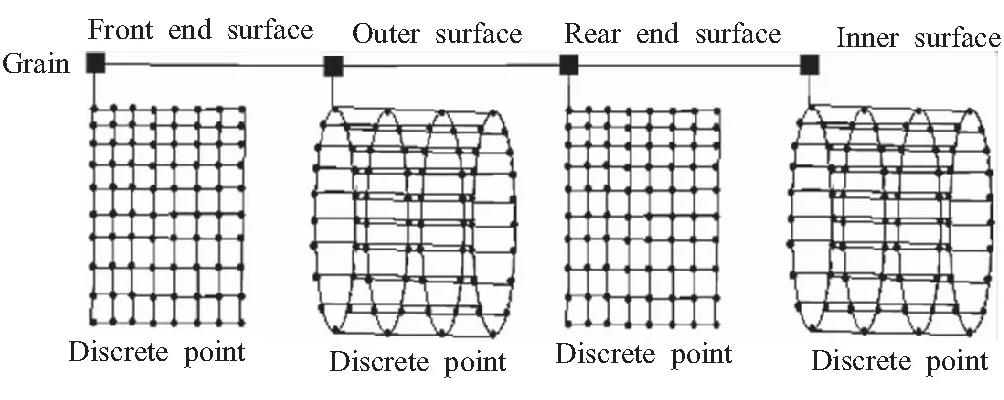
图7 离散点数据结构

2 燃面推移

2.1 与一维内弹道耦合推移

本文所采用的推移方法是燃面上的离散点沿燃面法向推移一定距离(肉厚)，该肉厚由该点位置处的燃速乘以指定的推移时间步长得到，而每一推移时刻的各点燃速由一维内弹道计算结果来确定。一维内弹道控制方程组如下：

(1)

当某一推移时刻装药的燃面、通气面积等几何特性已知，根据推进剂性能、发动机尺寸，使用速度侵蚀燃烧公式将侵蚀效应考虑进去，以四阶龙格库塔法求解一维内弹道微分方程组式(1)，计算出此刻的燃气质量流率，以及装药燃速、温度、密度、压力等各物理参数沿发动机轴线方向的分布，可得到实时推力。然后，根据一维内弹道计算结果得到下一时刻每一个离散点应当烧去的肉厚，再进行集合拓扑处理后，又可得到装药新的几何特性，以进行新的一轮一维内弹道计算，直到装药燃烧完成。燃面推移和一维内弹道计算的结合，使得每一个时间步长的内弹道计算结果决定下一个推移步的燃面上每一点的推移肉厚，而下一个推移步的燃面推移结果又决定下一个推移步的内弹道计算结果。如此循环迭代，直到装药燃烧终止，可得到整个装药燃面推移过程中的内流场变化情况。

此外，在推移过程中还要根据设置的离散参数来判断离散点的疏密情况。在本文研究中，以装药初始离散出来的平均点间距为参考，当推移过程中出现同一链表行上两相邻点距小于参考值某个小数倍时，需要在该行链表上进行“点删除”处理；出现相邻两行链表间距小于参考值某个倍数时，要进行“链表行删除”处理；出现同一链表行上大于参考值的某个倍数时，要用直线拟合插值法在两点间进行“点插入”处理；出现相邻两行链表间距大于参考值某个倍数时，同样要用直线拟合插值法在两行链表间生成新的链表行进行“行插入”处理。

2.2 面积计算方法

装药的燃面推移过程中需要用到面积计算，而装药侧面和端面的面积计算方法并不相同。

无论是外表面还是内表面的面积计算，都可基于侧面上两相邻行链表构成的微元环面来进行，将侧面上所有微元环面面积累加，就能得到该侧面的面积。

图8为一车轮孔装药内表面微元环面。记微元环面的一闭合车轮边界轮廓边长L1，另一闭合车轮边界轮廓边长L2，微元环面的母线长l，装药设计根数为N，由微元环面上的微元梯形ABCD，可推导出整个微元环面面积计算公式：

S微元环面=N·l·(L1+L2)/2

(2)

该式适用于任意装药侧面的微元环面面积计算。

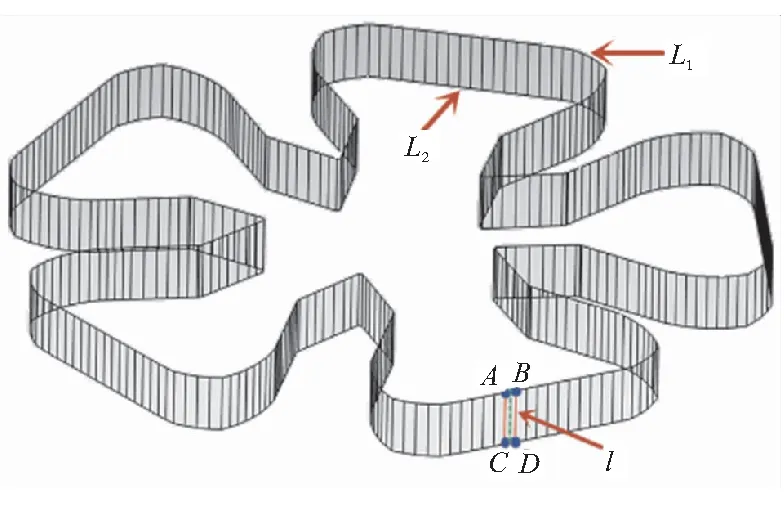
图8 车轮孔装药内表面微元环面

计算装药的端面面积和轴向截面面积时，只需要用到内外表面上的离散点链表。该计算可以利用二维多边形面积计算公式进行，端面上的离散点仅用作推移过程中的辅助定位推移。如图9所示的一多边形Ж，将各顶点按照逆时针方向标记，并设点Pi=(xi，yi)，则其面积计算公式为

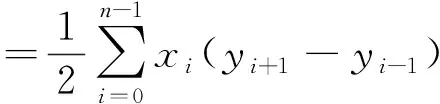
(3)

该式即为二维多边形面积计算公式，式中n表示顶点个数，索引需要与n进行模运算，有xn=x0和y-1=yn-1。

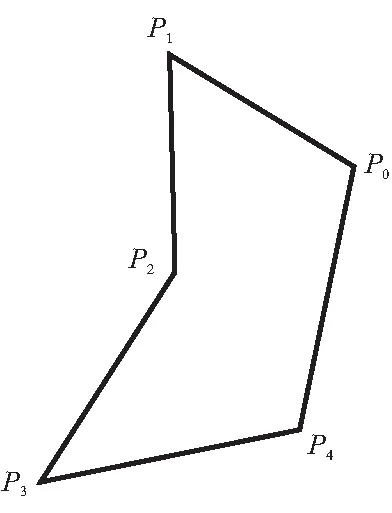
图9 二维多边形示意图

利用式(3)可实现实心装药的截面或者端面的面积计算。对于有内孔的单通道装药截面，可将其看成外侧边所构成的多边形与内孔边所构成的多边形组合，其截面积为外侧多边形面积减去内孔多边形的面积。

2.3 推移过程“面交汇”问题的处理

在装药燃面推移的过程中，不同面之间会出现奇异交汇的情况，使得装药表面拓扑失真。本文针对非槽的实心装药和单通道装药，可将“面交汇”可归纳为三类：面交叉、面脱落以及面破碎。面交叉和面脱落只发生在邻面之间，即只发生在侧面与端面之间，且由于端面离散点不参与面积计算，故判定标准只需要考虑侧面即可；而对于面破碎，通常由于装药几何尺寸特点，则只发生在内外侧表面之间，余药的产生与此相关。

“面交叉”是指装药上侧面的原边界脱离了对应端面，且在侧面内部形成了与端面新的接壤边界。以某端面燃烧的圆柱孔装药为例进行说明，图10所示为某一圆柱孔装药的半剖图，当装药开始端燃，侧面与端面会产生面交叉，比如图10中红线圈出位置。图11为该面交叉情况的简单示意图。图11中，箭头方向表示端面燃烧推移方向，下同。此时，点A所在的原边界链表节点行脱离了端面。处理方法为在侧面找到另一链表节点行作为新的边界，并按照拟合趋势挪动到端面处以贴合端面，再将侧面上多余的超出链表节点行删去。对应在图11中，则是删去点A所在的链表行，点B所在链表行作为新的边界。

图10 圆柱孔装药半剖图

图11 面交叉示意图

“面脱落”是指装药侧面与端面的接壤边界发生脱落，产生了缝隙，需要增加离散点使端面或者侧面脱落增加面积，以此来保持两相邻面的边界接壤。举例如图12所示，为一内孔燃烧的锥孔装药半剖图，红线圈出部分会出现面脱落。图13为处理过程简易示意图。图13中，箭头表示内表面推移方向，虚线AA1表示将扩展增加的内表面部分。

图12 锥孔装药半剖图

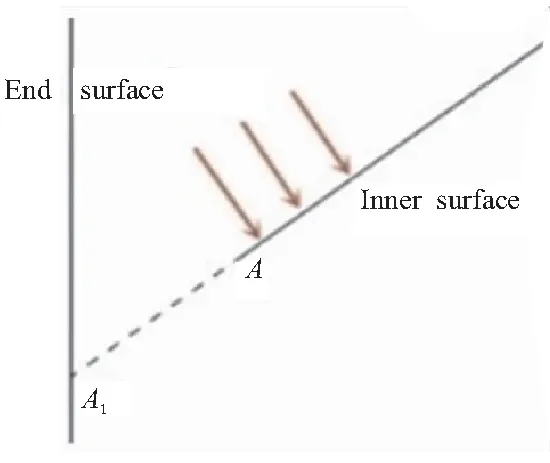
图13 面脱落示意图

“面破碎”指的是装药原本不相邻的内外表面产生了交集，使得这两个面互相分割破碎。该情况多发生在装药燃烧即将结束阶段。如图14所示，是星孔装药内孔燃烧推移过程中某一时刻的情形，经过一次推移后，形成了面破碎，形成多块余药。图15为该面破碎过程的截面轮廓图，由该图右边截面轮廓可看出，装药内外表面轮廓线部分重叠，这些重叠部分在实际燃烧过程中已经不存在，剩下的未重叠部分形成了若干块余药。但面破碎情况不一定都是形成多块余药，比如内孔燃烧的圆柱孔装药由于侵蚀效应的存在，其装药末端会比装药头部先烧完，末端处的装药内外表面相互交叉分割的面破碎过程并不会导致多块余药产生，只会使装药逐渐缩短。此时的处理方法是将实际物理已经不存在的重叠部分的离散点标记，在后续的燃面推移中不参与计算、不进行推移即可。

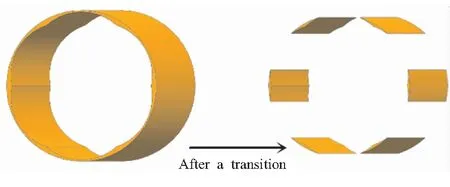
图14 星孔装药面破碎

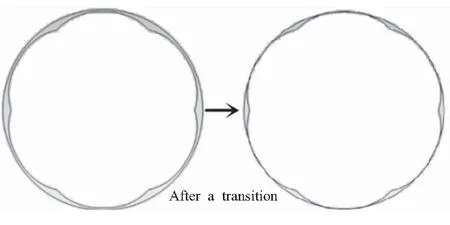
图15 星孔装药面破碎轮廓图

2.4 推移过程“奇异点”的处理

燃面推移过程中同一面上还会出现奇异点，使得计算失真。与面交汇一样，只需要考虑侧面即可。根据奇异点形成的原理不同，将其分为三类：错位圆弧点、交叉点以及行奇异点。

“错位圆弧点”是装药侧面上的圆弧点，这些点经过一次推移后，穿过圆弧的圆心抵达另外一端，形成奇异错位。举例如图16所示，为一内孔燃烧的星孔装药，红线圈出的星根处容易在推移过程中出现本类奇异点。其产生过程如图17所示，图17中箭头指示方向依旧为燃面推移方向，星根圆弧AB经过一次燃面推移到达圆弧A1B1产生了拓扑奇异错位，这些奇异点即为错位圆弧点。处理方法为用线段相交函数判断识别并剔除该类奇异点。所示情况处理后的轮廓线如图18所示。

图16 星孔装药错位圆弧点发生处

图17 错位圆弧点示意图

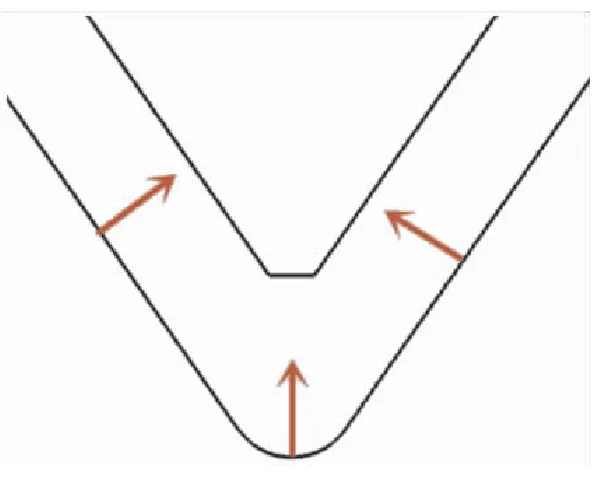
图18 错位圆弧点处理后示意图

“交叉点”主要出现在装药内外表面的尖角处，由于尖角的两侧推移法向夹角小于90°，在某一推移时刻经过一次燃面推移后，该处产生轮廓线奇异交叉，这种尖角上的奇异点就是交叉点。如图19所示，一车轮孔装药内孔燃烧，在某一时刻产生了如图19中红线圈出部分的尖角。该尖角经过一个推移时间步长、离散点沿着燃烧方向推移一定肉厚后，会出现交叉点，如图20所示。该类点的处理同样是通过线段相交函数判断识别，然后删去交叉点以及交叉点之间的离散点，将剩下的离散点重新构成链表行。

图19 车轮孔装药尖角产生

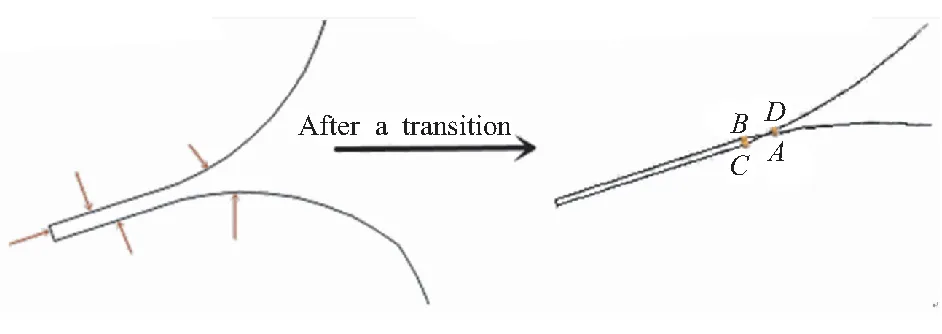
图20 交叉点产生示意图

“行奇异点”一般出现在相对于装药轴线有一定拔模倾角的装药侧面上，且经常以整行链表奇异的形式出现。有的装药侧面在轴线的不同位置有不同的拔模倾角，如果这恰好导致侧面上相邻部分沿燃烧推移法向产生相对推移，那么在推移过程中，侧面就会出现一些链表行的排列顺序与空间顺序不一致的情况，将这种链表称为奇异行，奇异行上的点称为行奇异点。图21为一内孔燃烧的锥柱孔装药，图中红线圈出部分即为在推移中会出现奇异行的位置。图22显示了该位置奇异行产生的过程，图中轮廓线的点代表该位置处有一个行链表。判断识别并删除奇异行，按照原有空间顺序编织侧面上剩下的链表，使其重新组织为面网格，即可消除此类奇异。

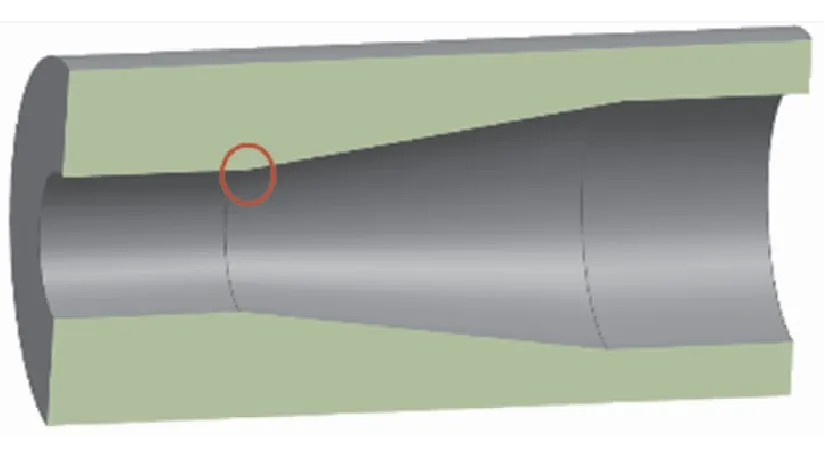
图21 锥柱孔装药半剖图

3 实际应用验证

3.1 算例

为检测研究成果对模拟装药实际燃烧的计算效果，对某发动机装药进行了计算预测。该装药长度为730 mm，装药外表面为三瓣异型结构，最大外直径为φ64.3 mm，内孔为三辐车轮状，三维模型示意如图23所示，其轴向截面轮廓结构见图24。

图23 装药三维示意图

图24 装药截面图

已知该发动机装药主要成分有硝化棉、硝化甘油、氧化镁、硬脂酸铝等，其柱剖燃速测试结果见表1。该装药推进剂成分类似双基药，但由于各成分比例未知，本文选择用双芳镁-3推进剂的性能参数作为参考估计，在表2中给出该装药推进剂其他性能参数的经验估计值，其中Vth为速度侵蚀函数公式中的侵蚀界限流速，Kv为速度侵蚀函数公式中的系数。装药不包覆，两侧面两端面均为燃面，其发动机设计参数装药根数为1，燃烧室内径为φ71 mm，燃烧室长度为740 mm，喷管喉径为φ27 mm，喷管出口直径为φ68 mm。

表1 装药柱剖燃速测试结果

表2 装药推进剂部分性能参数估值

表1中，燃速公式计算所用压强p的单位为MPa，依照公式计算得到的燃速单位为mm/s。该装药模型的离散参数设置周向分布点240个，轴向分布点个数选择对应的装药设计程序的推荐值173，燃面推移计算中的推移时间步长设置为0.006 s，分别演算预示环境温度为-55、20、60 ℃下的燃面推移结果，并与实验测得结果进行对比。

3.2 结果分析

图25～图30分别为-55、20、60 ℃下的燃烧室头部位置计算预测结果与实验测量结果曲线图。

图25 -55 ℃下p-t曲线对比

图26 -55 ℃下F-t曲线对比

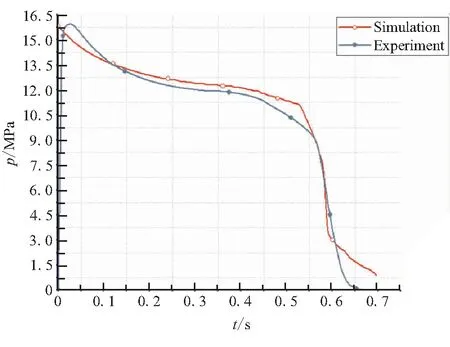
图27 20 ℃下p-t曲线对比

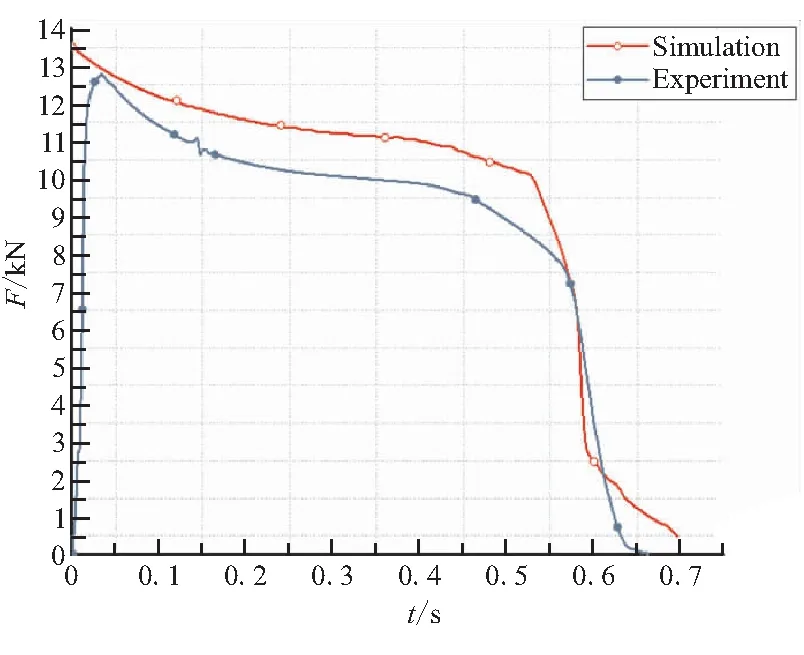
图28 20 ℃下F-t曲线对比

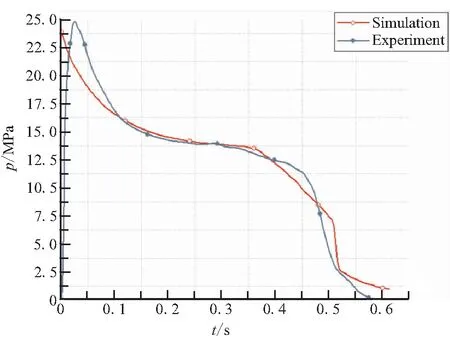
图29 60 ℃下p-t曲线对比

图30 60 ℃下F-t曲线对比

分析上述三种工作环境温度下的推移计算结果与实验测量结果对比曲线，发现它们变化趋势一致，且相比于实验测量值，计算预计的压强曲线最大峰值相对误差不超过3.7%，推力曲线最大峰值相对误差不超过6.8%，以压强低于1.5 MPa为工作结束点计算的工作时间误差不超过6.8%，可认为在该实验中，燃面推移计算结果在一定精度范围内能够较好地预示装药实际燃烧情况，表明计算方法是正确的。计算中的离散点数和计算步长选择能够满足计算精度要求，其带来的误差相对于图中的主要误差来源可忽略其影响。对比图中计算预测曲线与实验测得值存在较大误差的主要来源，一方面是因为计算使用的是一维内弹道，忽略装药点火过程，直接认为装药初始状态即为平衡压强状态，与实际的起始点不同，峰值有差异，且后效段只是近似处理，不一定符合实际；另一方面，则是因为计算用的推进剂性能参数是估计值。事实上，如果推进剂计算时用的性能参数是准确值，那么燃面推移计算结果将进一步契合装药实际工作燃烧情况，提供更好的预示效果。