正弦曲边负泊松比蜂窝结构面内冲击性能研究
2021-07-14虞科炯徐峰祥
虞科炯, 徐峰祥, 华 林
(1.武汉理工大学 现代汽车零部件技术湖北省重点实验室,武汉 430070;2.武汉理工大学 汽车零部件技术湖北省协同创新中心,武汉 430070)
负泊松比多胞材料由于其轻质、隔振、高吸能、高阻尼等特性引起了国内外学者的广泛关注,有望成为航空航天、汽车、建筑、医疗等领域不可或缺的材料之一[1]。随着微纳加工及增材制造技术(AM)的发展,材料设计空间被显著拓宽,涌现了大量新型结构。不同于传统实体材料,负泊松比多胞材料的胞元结构直接决定材料整体性能[2-3]。在冲击载荷作用下,不同的胞元结构形式、排列组合方式都将对材料局部动态力学行为产生显著影响。因此,正确建立胞元微结构几何参数与多胞材料动力学的响应关系,是更好阐述负泊松比多胞材料变形机理的重要目标之一。
负泊松比多胞材料最早由Lakes[4]于1987年首次制备,其将聚氨酯泡沫放入铝制模具中,并对其进行热处理从而得到了具有内凹胞体的聚氨酯泡沫材料。自此以后,众多学者针对负泊松比材料进行了大量研究,并提出了形式各异的拉胀结构,其中内凹胞元结构的研究备受关注。而早在1982年,Gibson等[5]便提出了胞元两侧内凹的二维六边形蜂窝结构。之后,人们通过改变多边形内凹构型和数量,相继提出了双箭头胞元结构[6]以及星型胞元结构[7]等。例如,Wan[8]等分析了单胞结构参数对内凹蜂窝结构泊松比的影响后发现单胞的内凹程度会显著影响其结构泊松比。Gong等[9]采用理论结合仿真的方法研究了星形蜂窝胞体不同几何参数对其泊松比、杨氏模量、剪切模量等的影响。韩会龙等[10]研究了星形节点周期性蜂窝结构的面内冲击动态响应特性,并总结出了该结构的密实应变以及平台应力的经验公式。张新春等[11]通过研究内凹六边形蜂窝结构讨论了胞元扩张角和冲击速度对其面内冲击性能和能量吸收机理的影响。可见,前期对负泊松比多胞材料的研究工作主要局限于某类结构的静力学性能以及负泊松比变化上,近些年才陆续开展冲击载荷下结构的动力学演化特性和吸能机理研究。
正弦曲线拉胀结构最早是由Dolla等[12]提出,其将该结构旋转成圆柱状并应用于心血管支架设计中,从而得到了比普通支架更高的周向强度和动脉壁支撑表现。邓小林等[13]在此基础上研究了一种平面正弦曲线蜂窝结构,研究表明该结构的轻微拉胀效应可增强其平面内能量吸收能力。在一定程度上,负泊松比正弦曲线蜂窝结构可看作是传统内凹六边形蜂窝结构的变体,但其胞元几何参数更少,且易于实现各参数的联动调整以及蜂窝自动化参数建模。因此,有必要将正弦曲线引入常规内凹六边形结构进行面内冲击性能研究,进一步澄清胞元微拓扑结构变化对材料动力学演化特性的影响。
本文在传统内凹六边形蜂窝结构的基础上,提出一种基于正弦曲线的负泊松比蜂窝结构,通过讨论胞元振幅、冲击速度以及胞壁厚度对其面内冲击性能和能量吸收机理的影响,建立负泊松比多胞材料动力学冲击特性与胞元微结构几何参数的内在关系,从而为内凹胞元的设计提供新的思路。
1 计算模型
1.1 蜂窝几何结构
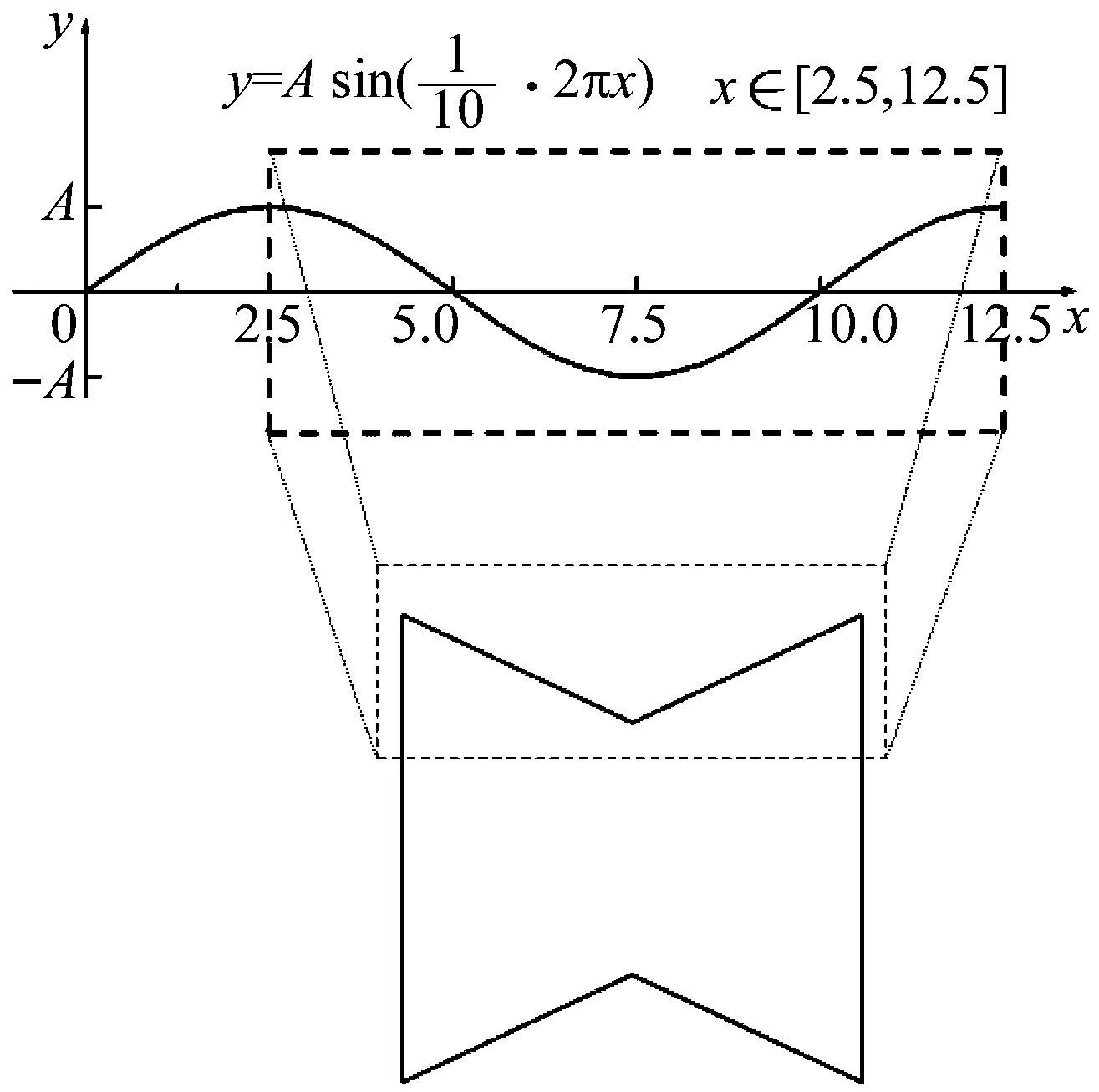
图1 正弦曲线的提取
取图1中虚线框内正弦曲线的一个周期长度,将其引入到下方传统内凹六边形胞元中,从而得到如图2所示的负泊松比蜂窝结构内凹胞元。其中,l1为上下对称分布的两条正弦曲线的周期长度、l2为胞元两侧臂长、t为壁厚、b为胞元的面外厚度。

图2 负泊松比蜂窝结构的胞元示意图
为了对不同负泊松比蜂窝结构进行面内动力学响应分析,本文将胞元内正弦曲线的振幅变量A设定在0.5~1.5 mm,采用相同的单胞臂长和壁厚建立由不同负泊松比胞元填充而成的蜂窝几何结构模型,如图3所示。

(a) A=0.5 mm
1.2 有限元模型
本文采用HYPERMESH/LSDYNA联合仿真进行非线性动态显式分析。如图4所示为正弦曲线蜂窝结构的面内冲击模型示意图。其中,蜂窝试件被置于左右两块刚性板之间,长度为L1,宽度为L2,分别由不同振幅的正弦曲线胞元填充。研究表明,在x、y方向上排列胞元的数目超过10时,结构的动态响应更加稳定。为有效捕捉试件变形特征,试件在x、y方向上的胞元数目分别为16和15。模型加载时,左端刚性板固定,右端刚性板以恒定速度v沿x轴负方向冲击试件。

图4 正弦曲线蜂窝结构面内冲击模型示意图
其中,蜂窝材料为金属铝,采用理想弹塑性模型,沿z轴方向的面外厚度为1 mm,左右刚性板均定义为刚体,具体材料参数如表1所示。计算过程中蜂窝结构选用SHELL163薄壳单元进行离散,为保证计算精度和收敛性,沿厚度方向定义5个积分点。经过多次试算和灵敏度分析,最终确定网格尺寸为0.7 mm。采用与文献[14-15]一致的边界条件和接触设置,即蜂窝结构左端与固定端刚体绑定,上下两侧面内自由,右端与冲击端刚体之间采用面面自动接触算法,摩擦因数为0.17;为防止冲击后各结构相互穿透,蜂窝内部各胞元间设置单面自动接触算法。另外,为保证冲击过程中蜂窝始终满足平面应变状态,限制试件中所有节点的面外位移。

表1 蜂窝材料和刚性板材料参数
根据多孔材料理论和文献[16]对蜂窝材料相对密度的定义,具有负泊松比效应蜂窝材料的相对密度可表示为
(1)
式中:ρ*为蜂窝结构的表观密度;ρs为基体材料的密度;As为胞元实体部分的面积;Atotal为胞元总横截面面积;li为胞臂总长度;t为胞壁厚度;L1,L2为整个蜂窝结构试件的长度和宽度。
根据式(1),易知正弦曲线蜂窝试件的相对密度可由胞元的承载面积与其总横截面面积的比值给出。因此,本文通过计算胞元内上下曲线、两侧胞臂的总长及总横断面面积,得到了相同壁厚下,不同振幅蜂窝试件的几何参数以及振幅相同、壁厚不同时的蜂窝相对密度,如表2、表3所示。

表2 不同振幅正弦曲线蜂窝几何参数

表3 不同壁厚正弦曲线蜂窝的相对密度(A=1.00 mm)
1.3 模型可靠性
为了验证有限元模型的可靠性,本文建立了与文献[17]参数相同的计算模型,讨论常规六边形蜂窝材料的面内冲击变形模式。图5给出了刚性板以v=3.5 m/s的速度沿x轴负方向冲击六边形蜂窝时,试件在不同时刻的变形状态,两者的载荷-位移曲线如图6所示。由图可见,在材料参数、载荷参数和边界条件设置完全一致的情况下,本文计算结果与文献[14]中面内变形模式和载荷-位移曲线基本吻合,证明了该有限元模型的可靠性。此外,沙漏能是衡量网格质量好坏的一个重要指标,也是验证冲击仿真模型的有效方法。在该模型的冲击过程中,沙漏能和滑移能的总和小于总能量的5%,由此进一步证明了仿真模型的可靠性。
在对常规六边形蜂窝结构研究的基础上,本文将采用相同的方法建立正弦曲线蜂窝结构的有限元模型,用于讨论它们的面内冲击动力学性能。
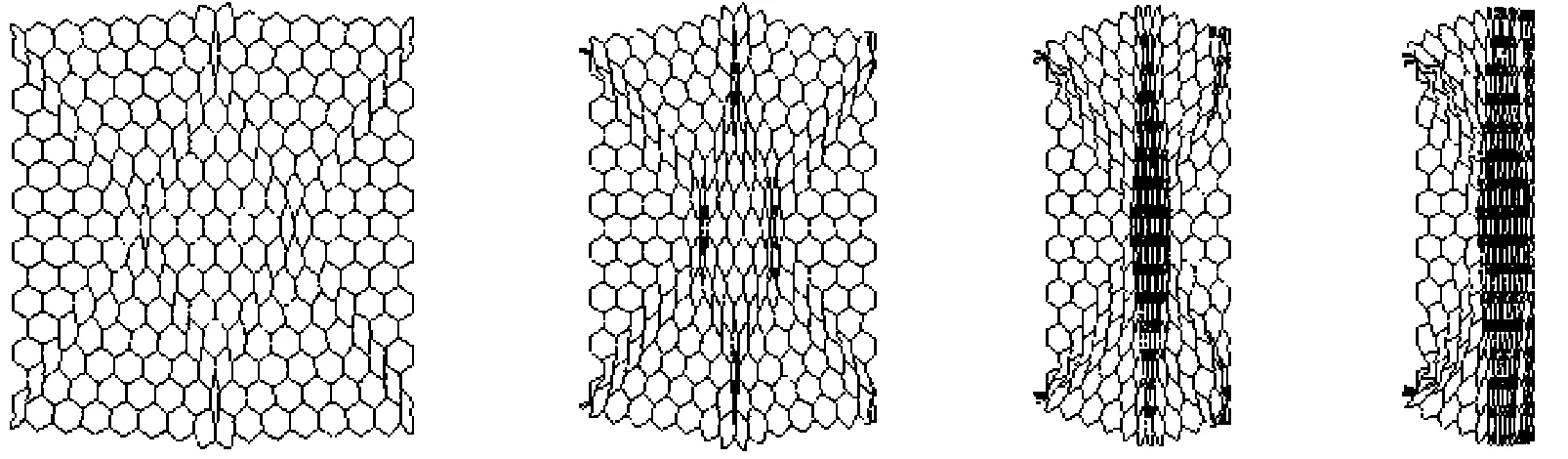
(a) 本文
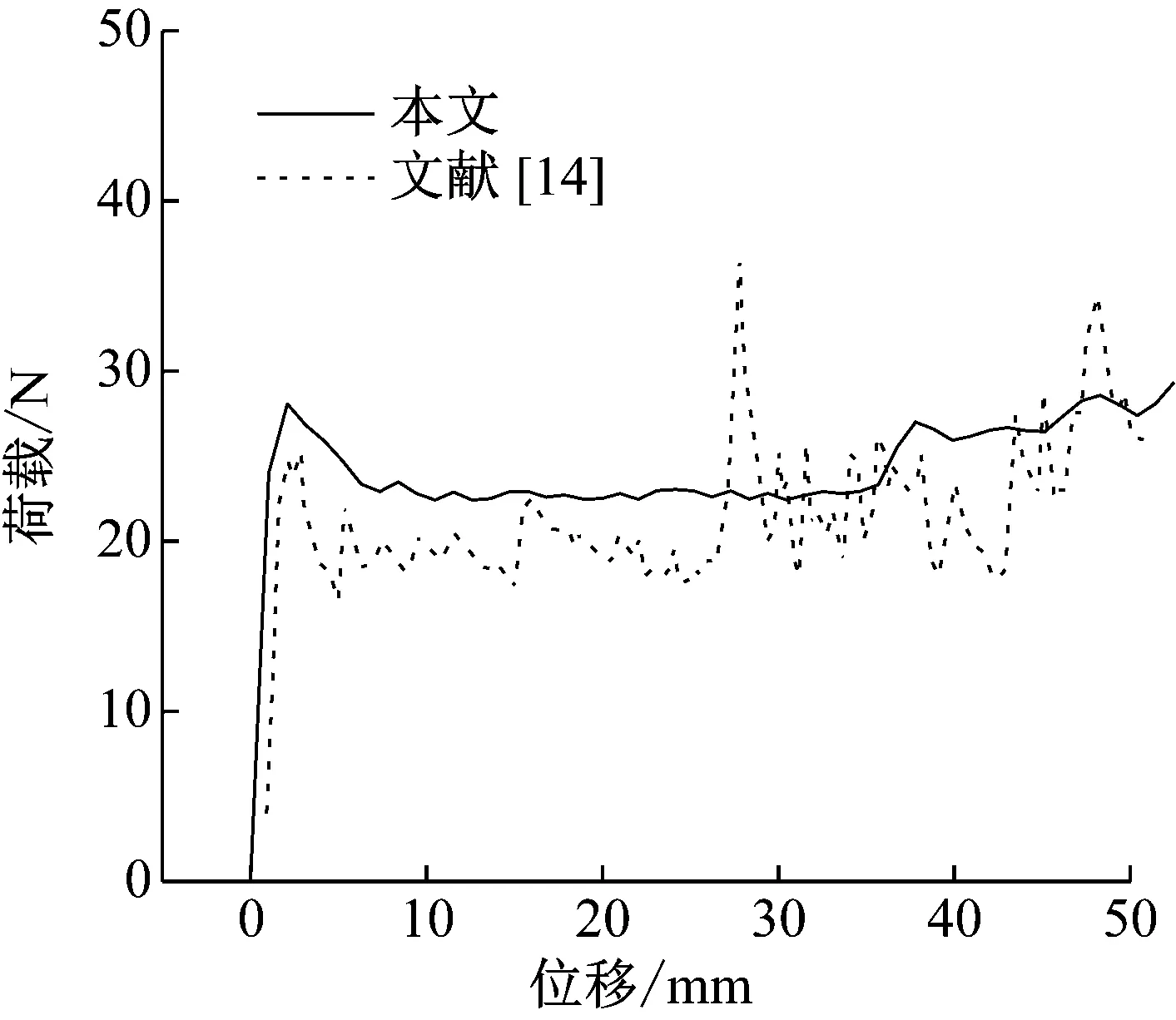
图6 常规六边形蜂窝沿x轴方向压缩的载荷-位移曲线
2 模拟结果与讨论
2.1 蜂窝结构的变形模式
变形的局部化和应力增强是蜂窝材料冲击响应的典型特征[18]。图7给出了两种冲击速度下,正弦曲线蜂窝结构在不同压缩应变状态时的典型变形模式。其中,名义应变ε为试件横向压缩位移与初始长度的比值。模型参数分别如下:A=0.75 mm、t=0.2 mm、v=10 m/s;A=0.75 mm、t=0.2 mm、v=90 m/s。在较低冲击载荷(v=10 m/s)作用下,如图7(a)所示,压缩开始时,由于胞元结构自身的负泊松比效应,整个蜂窝试件发生了明显的纵向颈缩现象。与此同时,局部变形带率先在右侧冲击端出现。在该弧形变形带上,靠近上下自由边界的胞元两侧受拉,而弧形带中部附近的胞元受压。随着压缩的进行,固定端开始出现局部变形带,并进一步加剧颈缩现象,而冲击端中部受压胞元逐渐溃缩成菱形内核,其上下侧变形带呈“人”字形由内向外扩张。当压缩至ε=0.5时,固定端同样开始生成菱形内核和上下对称分布的变形带,但其压缩变形始终滞后于冲击端。当ε=0.7时,蜂窝结构已不再有明显的颈缩现象而是向外扩张并呈现出局部对称的折叠结构。将冲击载荷提高到v=90 m/s,如图7(b)所示,变形模式发生了较大变化。此时,惯性效应起主导作用,蜂窝颈缩现象在压缩中后期才逐渐显现,其局部变形主要集中在冲击端并由冲击端逐层圧溃至固定端,最终趋于密实,这与其他结构形式的蜂窝材料变形模式基本相似。

ε=0.1
2.1.1 不同冲击速度下蜂窝结构的变形模式
图8给出了四种冲击速度下,具有不同幅值的正弦曲线蜂窝结构在ε=0.3时的面内变形模式。其中,各结构壁厚t=0.2 mm,曲线幅值A分别取0.5 mm、1 mm、1.5 mm,冲击速度v依次取3 m/s、10 m/s、30 m/s、90 m/s。

图8 正弦曲线蜂窝结构在不同冲击速度下的变形模式(t=0.2 mm,ε=0.3)
在v=3 m/s的低速冲击载荷作用下,不同振幅的蜂窝结构的面内变形均集中在冲击端和固定端,但局部应力分布有所不同。当ε=0.3时,A=0.5 mm的蜂窝结构,其冲击端有明显的弧形变形带以及菱形内核雏形;固定端则呈现出纵向的颈缩现象和y向变形带;蜂窝中间部分的胞元以行为单位向一侧扭曲且关于结构x向中轴对称交错分布。而此时A=1 mm的蜂窝结构冲击端的菱形内核已趋于密实且在纵向排列有不同于前者的“人”字形局部变形带,其中间胞元则基本不变。至于A=1.5 mm的蜂窝结构,其两端变形相似且应力分布相对于前两种结构更为分散,中间部分的胞元整体扭曲也更明显。由此可知,A=1.5 mm的蜂窝结构变形在三者中最为均匀,A=1 mm的蜂窝结构变形波动最大。
当v=10 m/s时,惯性效应开始显现,各蜂窝结构的纵向颈缩现象更为明显,冲击端的变形带开始逐层挤压中间胞元;固定端的变形现象则被削弱,振幅较小的蜂窝结构均只出现程度轻微的弧形变形带。各蜂窝两端的变形存在较大差距,只有A=1.5 mm的蜂窝结构变形带明显且近似于三角形。
当v=30 m/s时,各蜂窝结构的颈缩现象依然可见,但面内变形基本上发生在冲击端,固定端的少量变形也随着振幅的增大而进一步减轻。随着冲击速度的逐步增大,惯性效应不断增强,当v=90 m/s时,各蜂窝结构呈现出从冲击端到固定端逐层圧溃的变形模式,这与常规蜂窝结构基本相似。
通过以上分析可知,正弦曲线蜂窝结构的面内变形模式与曲线幅值和冲击速度有一定的关系。当中低速载荷冲击时,曲线幅值越大,局部应力分布越分散,结构面内变形越均匀;当高速载荷冲击时,振幅对蜂窝结构变形模式的影响基本可忽略不计。
2.1.2 不同厚度下蜂窝结构的变形模式
图9给出了冲击速度v=30 m/s时,具有不同胞壁厚度的正弦曲线蜂窝结构在ε=0.45时的面内变形模式。其中A=1 mm,厚度t分别取0.1 mm、0.2 mm、0.3 mm、0.4 mm。

(a) t=0.1 mm
由图9可见,壁厚较小的蜂窝结构在冲击端的局部变形带比厚度大的蜂窝密实,而其在固定端的应力变形则相对较小,这使得该结构两端的变形差距明显。由此可知,在中高速冲击时,厚度越小的蜂窝结构,其局部应力分布越集中,面内变形波动越大;因此,在一定程度上增大胞壁厚度可使蜂窝结构面内冲击变形更加均匀。
2.2 蜂窝结构的动态响应分析
蜂窝面内压缩的名义应力、名义应变为
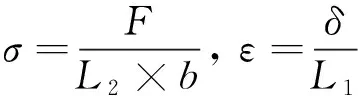
(2)
式中:F为接触反力;b为蜂窝面外厚度;δ为蜂窝压缩位移;L1,L2为整个蜂窝试件的长度和宽度。
基于式(2),图10、图11给出了不同振幅的正弦曲线蜂窝结构在四种冲击速度下,固定端和冲击端的面内冲击响应曲线。由图可见,在冲击过程中,正弦曲线蜂窝结构变形具有与常规蜂窝结构总体相似的动态响应规律,即压缩初始时近似的线弹性阶段、达到初始应力峰值后相对稳定的平台阶段以及应力陡升的密实化阶段。图10中固定端的名义应力应变曲线表明:在振幅一定时,固定端的初始应力峰值和平台段的应力波动幅度均随着冲击速度的增大而有小幅提高。当冲击速度较大(v=90 m/s)时,变形起始阶段存在某些时刻应力值接近于零的滞后现象且幅值越小,滞后现象越明显。对此现象合理的解释是蜂窝试件受冲击后,冲击端胞元被迅速压缩,但固定端受力较迟且与支撑刚体存在局部节点的短暂分离,因此产生向试件内部传递的卸载波,同时,由于负泊松比效应,上下侧材料纵向收缩抵御高速冲击,从而出现应力滞后[19]。
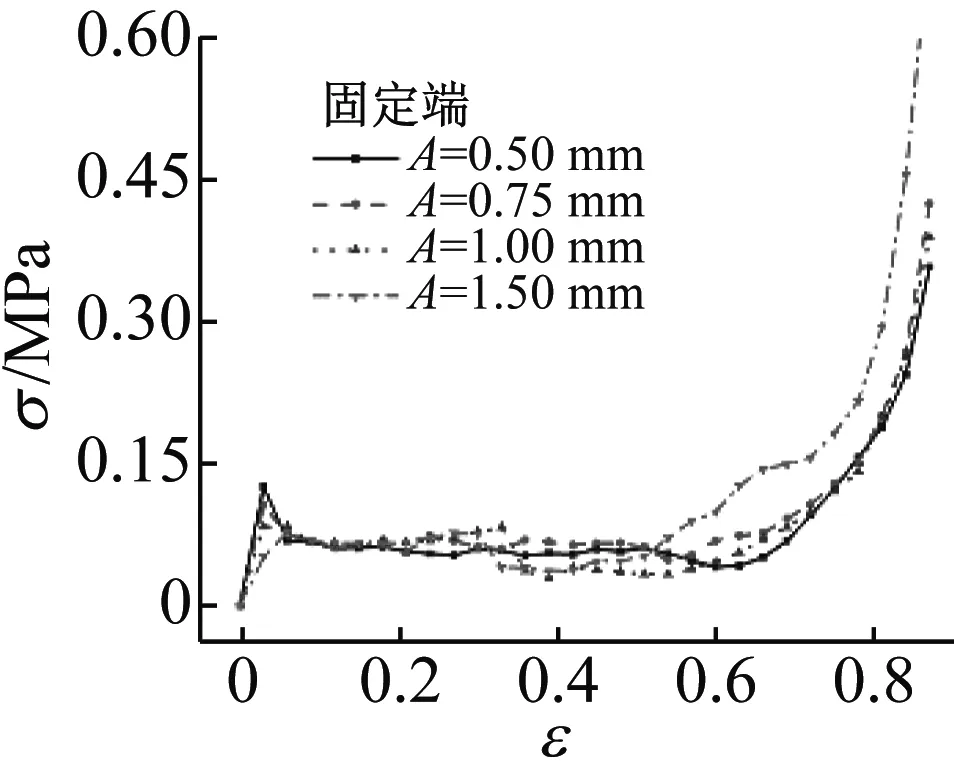
(a) v=3 m/s

(a) v=3 m/s
与固定端相比,图11中冲击速度对冲击端的应力波动影响更为明显。在低速载荷(v=3 m/s)冲击下,名义应力应变曲线与固定端基本相似,但随着冲击速度的增加,冲击端的初始应力峰值有了大幅的提高。从图11(c)、(d)中可以看出,在中高速载荷冲击下,曲线幅值越小,冲击端应力波动幅度越大,相应的平台段应力越小,而这些应力波动主要是冲击过程中,胞元快速坍塌并逐行圧溃、应力波在圧溃区传播所致。
2.3 平台应力与能量吸收特性
蜂窝材料的平台应力定义为
(3)
式中:εcr为屈服应变,即初始应力峰值所对应的名义应变;εd为锁定应变,可由名义应力再次达到初始应力峰值时所对应的应变确定;σ(ε)为随名义应变而变化的名义应力。
基于式(3),图12给出了不同冲击速度下正弦曲线蜂窝结构在冲击端和固定端的平台应力。由图可知,随着冲击速度的增加,不同振幅蜂窝冲击端的平台应力均明显增大,而固定端的平台应力基本保持不变且相对较小。由图13进一步可知,蜂窝结构冲击端的平台应力随振幅的增加而不同程度的增大,其中冲击速度越大,平台应力增幅越明显,其结果与文献[11]基本一致。
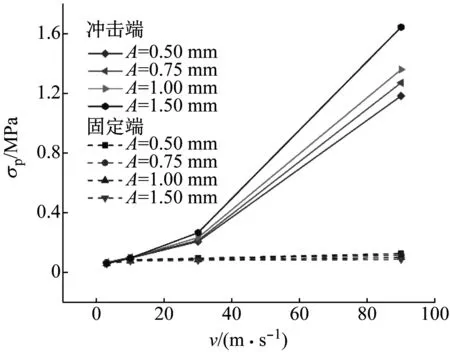
图12 不同冲击速度下正弦曲线蜂窝的平台应力
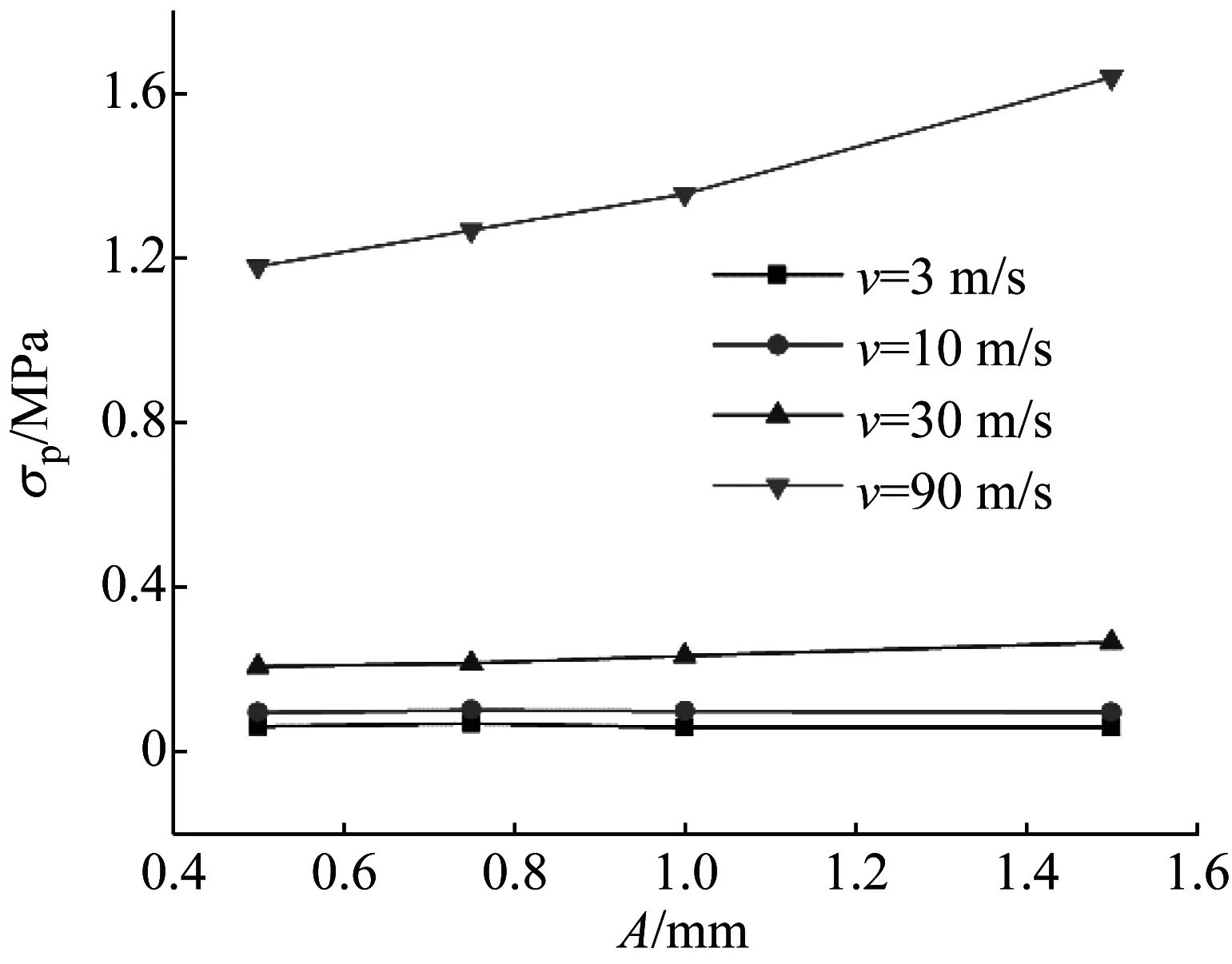
图13 正弦曲线蜂窝冲击端的平台应力随振幅的变化
为了分析蜂窝厚度对平台应力的影响,图14给出了不同厚度正弦曲线蜂窝在不同冲击速度下的响应情况。取振幅A=1 mm的正弦曲线蜂窝结构在t=0.1 mm、0.2 mm、0.3 mm、0.4 mm和v=3 m/s、10 m/s、30 m/s、90 m/s下的冲击响应情况进行比较。结果表明,蜂窝厚度是影响结构平台应力的关键因素之一。随着厚度的增加,固定端和冲击端的平台应力在不同冲击速度下均有一定程度的增大。其中,固定端的增幅较为明显,但由于其平台应力值较小,故依旧保持在较低的应力水平;冲击端的平台应力增幅虽然不如固定端,但其增长净值相对较大,因此可在一定程度上解释增大壁厚可使蜂窝面内冲击变形更加均匀的现象。
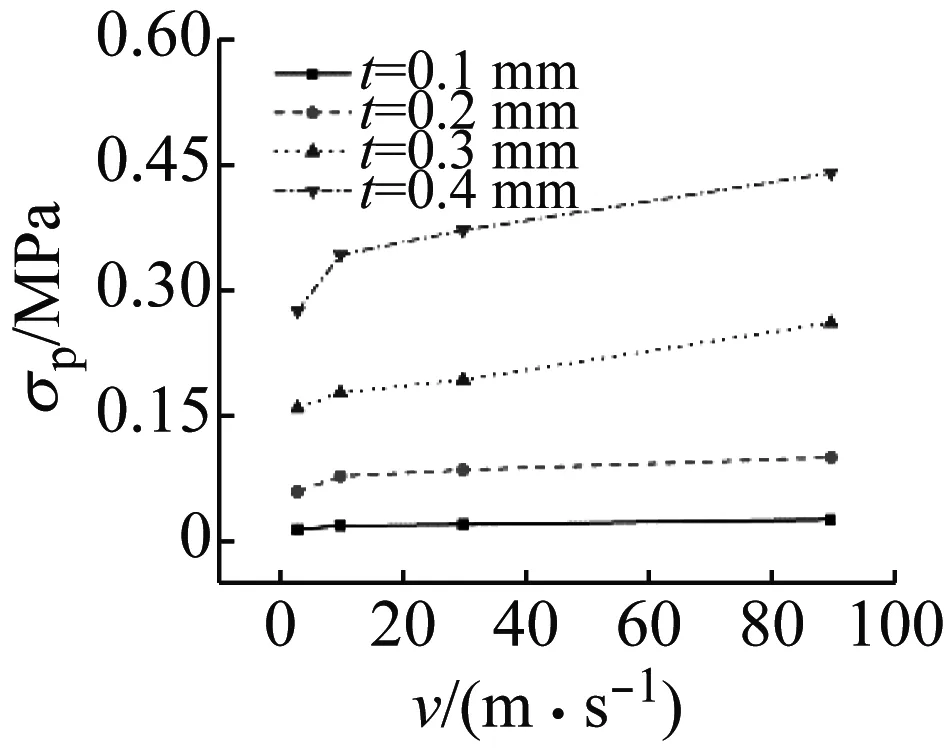
(a) 固定端
对于蜂窝材料而言,吸能特性评价指标能够反映其能量吸收能力,主要包括比吸能(specific energy absorption, SEA)和压缩力效率(crash load efficiency, CLE)等。其中,比吸能(SEA)即材料单位质量吸收的能量,可以表示为[20]
(4)

(5)
式中:Fp、Fm分别为平台载荷、初始峰值载荷;σp、σm分别为平台应力、初始峰值应力。
图15所示为四种振幅正弦曲线蜂窝结构(相同壁厚)在不同冲击速度下的比吸能变化曲线。

(a) v=3 m/s
由图15可以看出:当v=3 m/s时,冲击起始阶段正弦曲线蜂窝结构的振幅越小,能量吸收能力越好。随着压缩量的增大,振幅较大的蜂窝结构负泊松比效应凸显,在ε=0.4时,振幅A=0.75 mm的正弦曲线蜂窝的吸能性能超越了A=0.5 mm的正弦曲线蜂窝,并在余下的冲击过程中保持领先。而A=1 mm和A=1.5 mm的两种正弦曲线蜂窝由于其相对密度较大,使得总体的比吸能水平与振幅较小的两种蜂窝结构有明显差距。值得注意的是,振幅A=1.5 mm的正弦曲线蜂窝的比吸能在ε约为0.7时反超了A=1 mm的正弦曲线蜂窝,呈现出快速上升的走势,并最终接近振幅较小的两种蜂窝结构吸能水平。这是由于A=1.5 mm的蜂窝结构面内变形时应力分散,变形模式更为均匀,而A=1 mm的蜂窝结构变形波动较大所致的。当v=10 m/s时,正弦曲线蜂窝结构的能量吸收能力反比于振幅大小,直到ε接近0.8时,不同振幅蜂窝结构的比吸能曲线才产生交点,此时各结构的吸能能力趋于一致,随后振幅A=1.5 mm的蜂窝结构的比吸能曲线快速上升,这说明一定冲击速度下,振幅较大的蜂窝结构在冲击过程后期其单位质量能量吸收能力较好。当v=30 m/s、90 m/s时,A=0.5 mm的蜂窝结构比吸能曲线始终高于其他大振幅蜂窝结构,其中振幅越小,吸能能力越好。这是由于在高速载荷冲击下,大振幅蜂窝结构的负泊松比效应尚未完全显现,结构便已从冲击端开始被逐层圧溃。由上述分析可知,随着冲击速度的增大,不同振幅的正弦曲线蜂窝结构的比吸能均有所增加,在中低速冲击时,改变振幅大小对蜂窝结构的能量吸收能力有较大的影响;在高速冲击时,惯性效应增强,蜂窝结构的振幅越小,相应的比吸能越大,但总体上各结构吸能水平差距较小。
图16所示为四种振幅正弦曲线蜂窝结构的压缩力效率随速度的变化曲线。可以看出:不同振幅的正弦曲线蜂窝结构的压缩力效率曲线均近似于“V”形,其中低速和高速冲击时的压缩力效率明显高于中速冲击。蜂窝结构的振幅越大,压缩力效率也越大,这表明结构能更有效地吸收能量,恰好印证了上文蜂窝面内变形模式中曲线幅值越大,结构面内变形越均匀的结论。
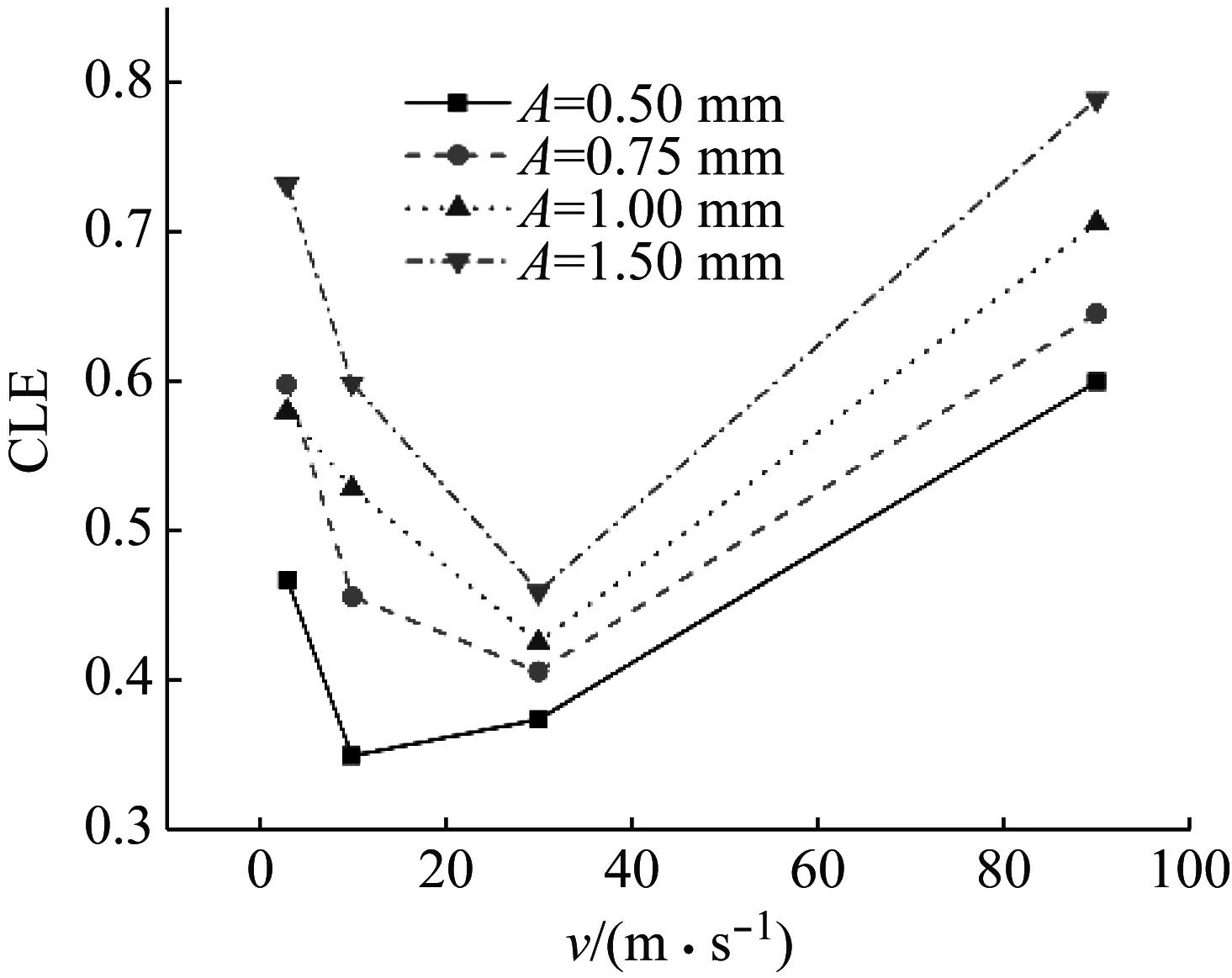
图16 不同振幅正弦曲线蜂窝的压缩力效率随速度的变化
结合图15和图16可以看出:低速冲击时,尽管振幅较小的正弦曲线蜂窝结构压缩力效率较低,但由于其相对密度较小,故比吸能较大,即单位质量能量吸收能力较好;高速冲击时,蜂窝结构具有较高的压缩力效率,因此比吸能较大,吸收的能量也相应增加,但由于惯性效应的存在,在蜂窝结构面内冲击变形模式中,不同振幅蜂窝结构间的压缩力效率差距可忽略。
为了对比正弦曲线蜂窝的吸能特性,本文选取上文中四种不同振幅正弦曲线蜂窝相对密度的平均值0.053 8,作为常规正六边形蜂窝的相对密度,另外取比吸能较大的A=0.5 mm正弦曲线蜂窝和与其内凹程度一致的负泊松比六边形蜂窝进行比较。三种蜂窝结构均采用相同方法建立冲击模型,结果如图17所示:在中高速冲击时,A=0.5 mm正弦曲线蜂窝和内凹六边形蜂窝的吸能曲线相近且长期位于常规正六边形蜂窝的上方,说明两者的吸能特性均优于常规正六边形蜂窝,此外,从图17(a)中可以看出,在v=30 m/s,ε约为0.4时,两者的比吸能优势相对于常规正六边形蜂窝达到了最大且均至少有40%的提高。进一步结合初始冲击力数据,在v=30 m/s时,A=0.5 mm正弦曲线蜂窝结构的峰值冲击力为75.6 N,而内凹六边形蜂窝为94.9 N,由此可知,尽管中高速时正弦曲线蜂窝结构与
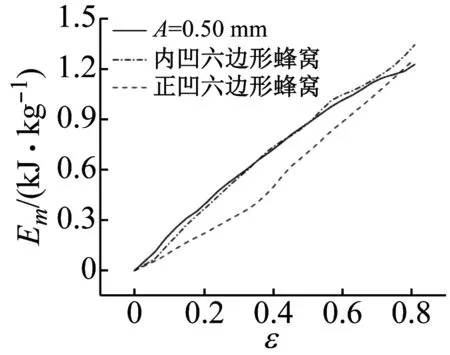
(a) v=30 m/s
内凹六边形蜂窝比吸能水平相近,但正弦曲线蜂窝结构具有低于后者20%左右的峰值冲击力,即更大的压缩率效率,这进一步证明了其优于其他常规结构蜂窝的吸能能力。
3 结 论
本文针对不同振幅、不同厚度的正弦曲线蜂窝结构,研究了不同冲击载荷作用下结构的面内动态冲击特性,从变形模式、动态响应以及吸能特性方面得到结论如下:
(1) 正弦曲线蜂窝结构的面内变形模式主要与振幅和冲击速度有关。中低速冲击时,振幅越大,结构面内变形越均匀;高速冲击时,惯性效应增强,振幅对蜂窝结构变形模式的影响较小。
(2) 在中高速冲击时,厚度越小的正弦曲线蜂窝结构,其局部应力分布越集中,面内变形波动越大。增大胞壁厚度可在一定程度上使蜂窝结构面内冲击变形更加均匀。
(3) 在相同的冲击速度下,增加正弦曲线蜂窝结构的壁厚可使其两端的平台应力增大。当壁厚相同时,蜂窝结构冲击端的平台应力随振幅的增加而不同程度的增大,其中冲击速度越大时,相应的平台应力增幅越明显;而此时固定端的平台应力始终较小且基本保持不变。
(4) 随着冲击速度的增大,不同振幅的正弦曲线蜂窝结构的比吸能均有所增加。在中低速冲击时,改变振幅大小对蜂窝结构的能量吸收能力有明显的影响,其中振幅较小的蜂窝结构总体吸能表现较好;在高速冲击时,振幅越小,则比吸能越大,但总体上各结构吸能水平差距较小。
由此可见,合理优化正弦曲线蜂窝结构的振幅、壁厚等参数,能够有效地提高正弦曲线蜂窝结构在不同冲击载荷作用下的吸能能力,并且获得优于内凹六边形蜂窝结构等其他常规蜂窝的能量吸收表现。
