一种基于时空瞬时稳定性的方位谱估计方法

王林生, 王慧婷, 刘志刚

(1.河南省工业嵌入式网络控制工程技术研究中心，河南 南阳 473009；2.河南工业职业技术学院，河南 南阳 473009；3.北京邮电大学 科学技术发展研究院，北京 100876；4.南昌大学安全仿真模拟实验室，南昌 330031)

空间方位谱估计一直是雷达、声纳等领域中重要的研究课题，为了降低空间方位谱估计方法对原始数据最低信噪比需求，人们常采用布阵与信号合成方式提高输出信噪比，等价于降低了空间方位估计方法对原始数据最低信噪比需求[1-2]。为了能够对360°水平范围内空间目标实现等分辨率方位估计，研究学者提出通过布放圆阵方式实现[3-6]；另外，为了提高圆阵空间方位谱估计分辨率，在信号处理方面，研究学者提出采用子空间分解方式实现高分辨方位估计(本文称之为子空间分解方法)，并对该方法进行了工程化应用[7-8]。

由于现有子空间分解方法在对一帧数据进行协方差估计中，首先将一帧时域多个采样数据通过傅里叶变换转换为不同频点频域数据，实现频域压缩采样；然后再对每一频点利用频域单个数据求取该频点协方差矩阵；最后通过多帧频域数据累积实现协方差矩阵估计[9-10]。由于受时频转换中频率分辨率限制，单帧时频转换需要一定长度时域数据，致使在空间数据非平稳时，难以通过频域多帧数据累积实现协方差矩阵估计，影响子空间分解效果，对实际应用带来了一定的限制[11-12]。为了提高子空间分解方法在实际应用中的稳健性，研究学者从混沌优化思想[13]、自适应迭代加权思想[14]、压缩感知思想[15-16]、滑动平均思想[17]提高了子空间分解方法的目标检测性能，但以上思想均是对如何实现协方差矩阵估计，并未考虑在协方差矩阵估计之前进行阵增益转换预处理。

针对基于子空间分解的空间方位谱估计方法稳健性问题，本文提出一种基于时空瞬时稳定的方位谱估计方法。该方法可将短时内获得的足够多的采样数据转换为协方差估计所用快拍数，通过多个快拍数据累积实现满秩协方差矩阵稳定获取，降低空间数据稳定性对子空间分解产生的影响；同时在无目标先验信息情况下，依据各子空间方位谱峰值索引离散度差异，通过对各子空间方位谱进行判决处理，降低背景噪声对最终合成方位谱影响。数值仿真及实测数据处理结果进一步验证了所述方法的有效性和可行性。

1 子空间分解方法

1.1 基本原理

(1)

式中:W(θ)=[ej2πfτ1,ej2πfτ2,…,ej2πfτN)]为导向权向量;N为传感器数。

(2)

1.2 空间数据影响分析

在频点fi上，第k帧数据的协方差矩阵可表示为

(3)

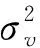
同时，由文献[18]可知，一次处理数据帧数K对子空间分解方法的影响可近似表示为

(4)

式中，σP(θ)为子空间分解方法所得空间目标方位估计方差。

由式(4)可知，在传感器数N一定时，一次处理数据帧数K对子空间分解方法影响较大。

2 本文方法

2.1 基本原理

由傅里叶变换分析可知，对于一帧多个时域数据经过傅里叶变换后，在频域同一频点只包含单个频域数据，再利用单个频域数据求取不同频点协方差矩阵时，容易出现非满秩现象，且会导致信干噪比损失较大。对此，本文依据空间目标信号时域瞬时稳定性，通过复解析变换，将多个时域数据转换为多个复域数据，通过多个复域数据的累积，提升协方差矩阵稳定性。

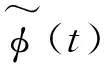
(5)

式中，w为角频率。

(6)

通过选择小波函数参数(如带宽参数、中心频率和尺度伸缩因子)，可在对接收阵拾取数据实现复解析变换处理中抑制分析频带以外背景噪声，具体证明可参考文献[19]。

其次，根据相位与时延之间的关系，在搜索角度θ上，对各传感器复域数据Y按τn=(rcos(θ-(n-1)α))/c进行时延补偿，c为声速，r为接收阵半径，α=2π/N，1≤n≤N，N为接收阵所含传感器数量，得经时延补偿后数据。

(7)

式中，φτn=[φτ1,φτ2,…,φτN]T，φ0=[φτ01,φτ02,…,φτ0N]T，τ0n=(rcos(θ0-(n-1)α))/c，θ0为空间目标相对接收阵方位。

(8)

最后，对延时补偿后的各子空间对应特征向量互相关矩阵求和，求取该帧数据各子空间对应空间方位谱；并利用各子空间对应空间方位谱峰值索引离散度差异[20]，对各子空间方位谱按式(9)进行加权处理，得到最终合成方位谱。

(9)

式中:由于不知道目标信源个数，方位求和加权处理中对所有子空间合成方位谱进行加权处理，I1×N=[1,1,…,1]1×N为1×N单位矩阵;αn为合成方位谱过程中第n个子空间对应的加权因子。

2.2 方法实现

本文方法可分为以下几个步骤实现。

输入：对接收阵拾取数据x(t)。

步骤1对接收阵拾取空间数据按式(6)进行复解析小波变换和分帧处理(相邻两帧之间按L=0.5I长度进行重叠处理)，得到K帧复域数据Y，并令处理数据帧号k=1；

步骤2按式(7)所示，在搜索角度θ上，对第k帧复域数据Y进行时延补偿；

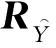
步骤4采用常规波束形成思想，按式(10)所示，得到第k帧数据对应的各子空间方位谱Pn(k,θ)，1≤n≤N；

(10)

步骤5更新搜索角度θ，重新执行步骤2～步骤4，直到θ=Θ结束，得到各子空间方位谱Pn(k,θ)在0°≤θ≤Θ上各个值；

步骤6搜索各子空间方位谱Pn(k,θ)，0°≤θ≤Θ，1≤n≤N最大值索引，得到该子空间方位估计值；

(11)

步骤7更新处理帧数据，k=k+1，重复执行步骤2～步骤6，直到k=K，则各子空间均得到K个方位谱Pn(k,θ)和方位估计值θmax(k,n)，k=1,2,…,K。

步骤8求取各子空间方位谱峰值索引的离散度，记为σθmax(n),n=1,2,…,N。

(n=1,2,…,N)

(12)

(k=1,2,…,K;n=1,2,…,N)

(13)

式中，Cm和M分别为最小二乘拟合系数和阶数。

步骤9在无目标先验信息情况下，根据各子空间方位谱峰值索引离散度求取各子空间方位谱加权因子。

n=1,2,…,N

(14)

步骤10利用各子空间方位谱加权因子对各子空间方位谱进行加权处理，得到下最终合成方位谱

(15)

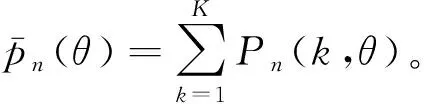
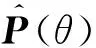
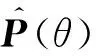
2.3 估计能力分析

令接收阵所在空间只存在1个空间目标，空间目标相对接收阵方位为θ0，对应子空间编号为N。由空间目标子空间方位谱所得方位估计值(最大值索引)范围为[θ0-Δθ0,θ0+Δθ0]，其中Δθ0为空间目标子空间方位谱对应方位估计误差；由非目标子空间方位谱所得方位估计值(最大值索引)范围为[θmin,θmax]，其中θmin和θmax分别为方位扫描角度最小值和最大值。令，空间目标和非目标对应子空间方位谱的方位估计值方差分别为σs和σn。

(16)

为了进一步说明本文方法通过对各子空间方位谱进行最大值索引离散度判决处理，可有效提高空间目标对应子空间方位谱在最终合成方位谱中的比重，降低了背景噪声对子空间分解方法的影响。

首先，对N-1个非目标子空间方位谱进行统计。对于非目标子空间方位谱，每个方位对应索引在每帧方位估计中出现概率相等。

(17)

然后，将空间目标方位谱方位估计值对应方差加入上式，可得到：

(18)

上式可进一步简化为

(19)

图1为不同方位估计范围所得方位估计方差理论值和仿真值。

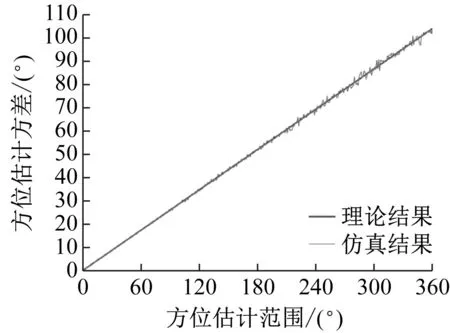
图1 不同方位估计范围下方位估计方差

当空间目标对应子空间方位谱每帧方位估计值均接近于空间目标方位真值时(Δθ0≈0°)，非空间目标子空间方位谱方位估计范围在0°≤θ≤Θ，由图1可得，σs<<σn，即

(20)

3 验证分析

3.1 数值仿真分析

为了进一步验证本文方法在方位估计方面的性能，接下来进行如下几方面数值仿真。

表1 数值仿真参数

3.1.1 多目标方位估计分析

数值仿真中，噪声为空间高斯白噪声经过128阶滤波器滤波所得带限噪声，频带宽度与目标信号带宽一致，信噪比计算方式为

(21)

式中:lg(·)为以10为底对数;var(·)为方差函数;sig(t)为目标信号;noise(t)为带限噪声;t为采样时刻。

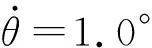
图2～图7仿真结果表明：在该仿真条件下，在无目标先验信息情况下，子空间分解方法已无法对空间目标实现方位估计，而本文方法可以对4个空间目标实现方位估计；在有目标先验信息情况下，子空间分解方法对空间目标实现方位估计效果远差于常规波束形成和本文方法；对于60°和68°处空间目标，常规波束形成已无法对其实现有效分离，而本文方法却可以很好地将其分开，进一步验证了本文方法保持了子空间分解方法在分辨率上的优势，相比常规波束形成具有较好的方位分辨率。另外，在背景噪声级方面处理上，本文方法好于常规波束形成，而子空间分解法最差。

以上现象原因在于子空间分解方法需要多帧数据的频域累积才能满足协方差矩阵的满秩条件，当空间数据存在不稳定时，会导致失配现象产生；而本文方法通过复域处理，采用一帧时域数据即可满足协方差矩阵的满秩条件，同时采用图 8所示加权因子αn对各子空间方位谱进行加权处理，在无目标先验信息情况下，有效提升了编号21～24子空间(空间目标信号子空间)方位谱在最终合成方位谱中的比重，降低了背景噪声对合成方位谱的影响。

3.1.2 方位估计性能统计分析

为了进一步验证本文方法对空间目标方位估计性能的统计特性，对上述仿真中60°处目标进行检测和方位估计统计分析，在SNR=-30 dB～0情况下，图9和图10分别给出了由子空间分解方法(先验信息已知)、子空间分解方法(先验信息未知)、常规波束形成、本文方法(先验信息已知)和本文方法(先验信息未知)进行500次独立统计所得目标检测概率和方位估计的均方根误差。

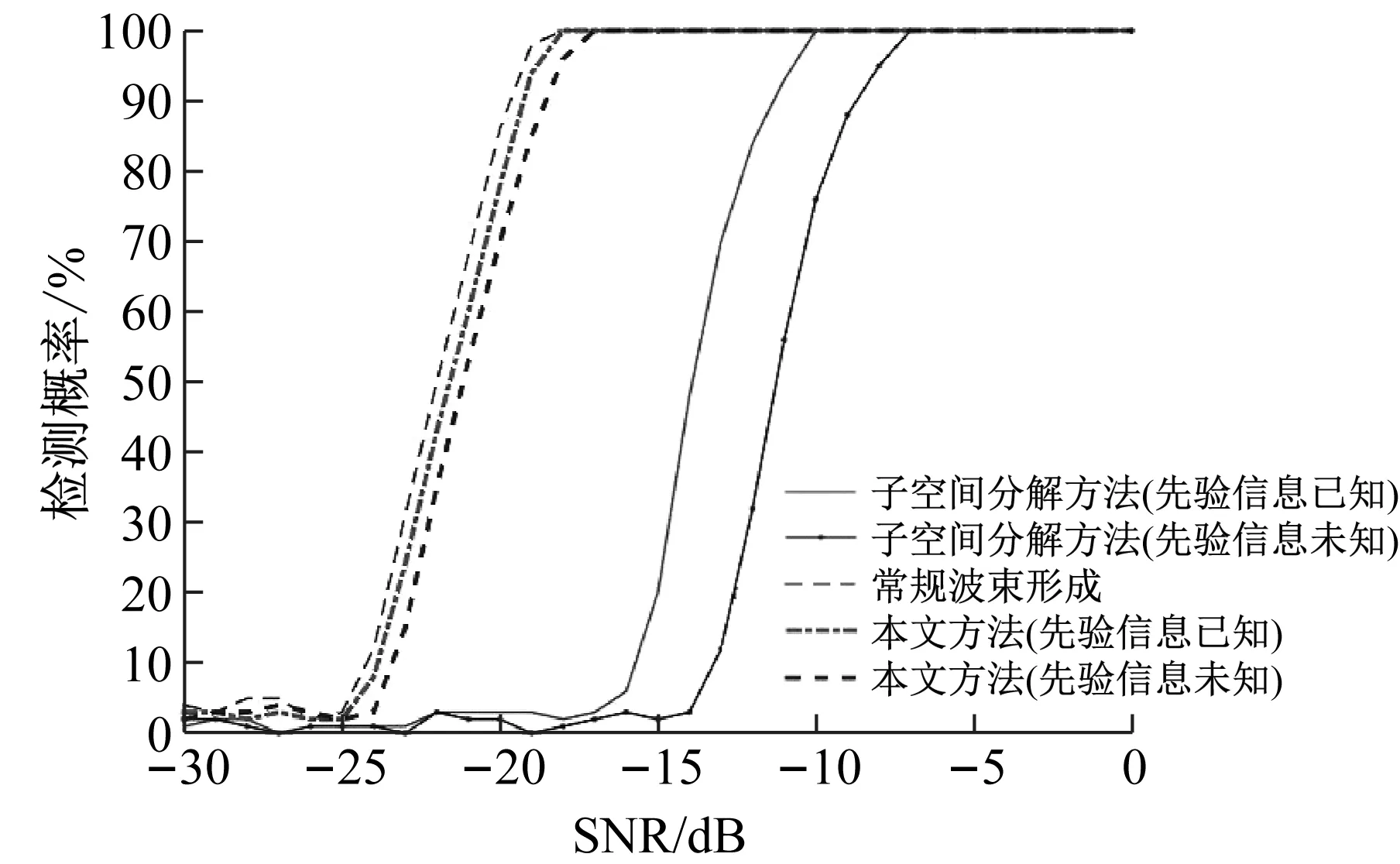
图9 5种方法所得目标检测概率

图10 5种方法所得均方根误差

由图9仿真结果可知，对于同一目标检测概率和均方根误差，子空间分解方法(先验信息未知)相比子空间分解方法(先验信息已知)对空间目标检测和方位估计的稳健性差于2 dB；而子空间分解方法(先验信息已知)相比本文方法(先验信息已知)和本文方法(先验信息未知)对空间目标检测和方位估计的稳健性差于6 dB以上；而本文方法(先验信息未知)与本文方法(先验信息已知)、常规波束形成基本一致；该结果进一步验证了本文方法采用复域处理，可将一帧时域多个采样数据转为多个复域数据，通过多个复域数据累积实现了满秩协方差矩阵稳定获取，降低了空间数据稳定性对子空间分解产生的影响；同时通过加权因子αn对各子空间方位谱进行加权处理，在无目标先验信息情况下，有效提升了空间目标信号子空间方位谱在最终合成方位谱中的比重，进一步降低了背景噪声对合成方位谱的影响。

3.2 实测数据处理分析

本次处理数据采用圆阵对未知多目标检测和方位估计试验所得，相关参数如表2所示。

表2 数据处理参数

本次处理数据环境噪声级约为70 dB@1 kHz.可视距离内存在多个目标，其中相对圆阵方位10°、30°、60°、90°、220°和270°为吨位较大船只，300°附近有1快速运行快艇，声级约为120～130 dB@1 kHz。具体处理过程如下：首先对处理数据采用复解析小波变换对1.5～2.0 kHz频段进行处理；然后对一次处理数据分K=78帧处理(单帧数据为512个采样数据，帧与帧之间重叠256个采样数据)，对每帧数据做傅里叶变换分析；最后对各频点作协方差矩阵估计、特征分分解、方位谱合成。处理中目标先验信息未知，图11～图15分别为子空间分解方法(先验信息已知)、子空间分解方法(先验信息未知)常规波束形成、本文方法(先验信息已知)和本文方法(先验信息未知)处理所得时间历程图。

对比图11与图15可知，本文方法所得方位历程图显示目标航迹清晰，目标方位明晰可辨；受空间方位分辨率影响，常规波束形成所得方位历程图对220°附近目标显示效果差于本文方法；受空间数据稳定性影响，子空间分解方法在该时段时间段内无法对10°、30°、60°、90°、220°和270°附近目标实现有效检测和方位估计，本文方法所得方位谱优于子空间分解方法，进一步验证了本文方法在无目标先验信息情况下，通过各子空间峰值索引离散度对各子空间方位谱进行加权处理，进一步降低了背景噪声对最终合成方位谱影响，相比子空间分解方法有更低的背景噪声级。

4 结 论

针对基于子空间分解的目标检测方法稳健性问题，本文提出了一种基于时空瞬时稳定性的方位谱估计方法。该方法依据空间目标信号时域瞬时稳定性，通过复解析变换，将多个时域数据转换为多个复域数据，通过多个复域数据的累积稳定获取了满秩协方差矩阵，降低了空间数据稳定性对子空间分解产生的影响；然后依据各子空间峰值索引离散度差异，对各子空间方位谱进行非线性加权理，降低了背景噪声对最终合成方位谱影响。数值仿真及实测数据处理结果表明，相比子空间分解方法，在不损失空间分辨率情况下，能够有效降低空间数据稳定性对协方差矩阵估计产生的影响，在无目标先验信息情况下，对最低信噪比的需求得到了6 dB以上的降低。