安全联锁设备SIL验证中的参数估计偏差分析*
2021-07-12李敏睿王海清姚竣瀚
李敏睿,王海清,姚竣瀚,毛 奇
(中国石油大学(华东)安全科学与工程系,山东 青岛 266580)
0 引言
国内化工企业尤其是涉及“两重点一重大”的大型企业按照中华人民共和国应急管理部〔2014〕116号文《关于加强化工安全仪表系统管理的指导意见》的要求广泛开展安全联锁系统评估与改造,以适应当前严峻的危化品安全生产形势要求。安全完整性等级(SIL),是衡量安全联锁系统安全水平的关键指标之一,即在一定时间和一定条件下,安全相关系统执行所规定的安全功能的概率[1]。根据功能安全标准IEC61508,SIL以联锁回路的平均需求时失效概率PFDavg作为验证依据。
功能安全标准IEC61508(下文统一简称为IEC61508)计算PFDavg时均假设相关设备的失效率为恒定值[2](即寿命分布服从指数分布),以化工安全设备为背景的PFDavg算法和SIL验证中,安全管理人员均是采用恒定失效率计算。但实际中,设备由于老化[3]、疲劳磨损[4]等因素,绝大多数机械、电子设备[5]的失效率随使用时间缓慢上升,在计算时导致PFDavg与实际值存在较大误差。不仅如此,IEC61508针对不同应用范围,推荐不同参数估计置信度[6],影响SIL验证的准确性,增加验证的不确定性[7],使得化工企业的生产装置处于欠保护或者过保护的状态,进而可能误导风险评判结果。
鉴于此,本文定量比较研究安全联锁回路在恒定和非恒定失效率情况下的2种算法,并对存在的偏差进行定量评估分析,以更好落实《关于加强化工安全仪表系统管理的指导意见》在国内化工企业的应用。首先使用蒙特卡洛仿真,获取符合工程实际的失效数据,进而使用极大似然估计求解出威布尔参数和指数参数,并运用威布尔分布PFDavg算法、指数分布PFDavg算法及IEC61508近似算法分别在70%和90%的2种典型置信度下得到3者PFDavg值随预防性维修周期的变化趋势,对SIL验证结果的影响进行对比分析。
1 失效截尾数据的蒙特卡洛仿真
本文主要研究目的是对比安全联锁系统设备的失效数据组分别在IEC61508近似算法,指数分布算法与威布尔分布算法下的可靠性评估差异,在结合与参考了安全联锁设备失效数据库、研究对象的大量历史失效数据后,得出1组可信度较高的失效参数,后使用这组参数在蒙特卡洛仿真中模拟生成一系列失效数据。这种方法能够满足本文同时针对指数分布参数估计和威布尔分布参数估计的需求。根据蒙特卡洛仿真的原理[8],基于MATLAB设计蒙特卡洛仿真算法流程,如图1所示。

图1 基于MATLAB蒙特卡洛仿真算法流程
蒙特卡洛仿真使用的仿真方法为概率积分变换方法,这种方法是将任意随机变量转换为均匀分布的随机变量,代入概率密度分布函数的逆函数,循环多次计算得到一系列失效时间样本值。
2 参数的极大似然估计
2.1 威布尔分布参数估计
假设失效数据服从威布尔分布,运用极大似然法和试错法求出威布尔分布的形状参数α和尺度参数β的估计值。使用极大似然法[9]求解威布尔参数估计值,如式(1)所示:
(1)
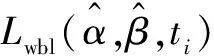

(2)

(3)
将式(3)带入式(2)中,如式(4)~(5)所示:
(4)
(5)

2.2 指数分布的参数估计
假设失效数据服从指数分布,可由指数分布I型截尾数据下的极大似然法求出失效率λ,指数分布的极大似然估计函数,如式(6)所示:
(6)

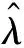
(7)
2.3 参数的置信区间估计
根据IEC61508,参数估计的置信度η不低于70%,同时在用于判断结构约束时要求置信度η不低于90%[10],在极大似然法估计的基础上,对参数进行不同置信区间估计以得出区间估计值。分别以70%和90%置信度为条件,研究和对比可靠性参数的区间估计值及其影响。
依据指数分布参数的区间估计算法[9],可计算出指数参数估计区间[λL,λU],如式(8)~(9)所示:
(8)
(9)
式中:η为区间估计的置信度;λL为指数参数区间估计下限值;λU为指数参数区间估计上限值;T为所有样本的总失效时长,h;χ2为卡方分布。
依据威布尔分布参数的区间估计算法[9,11],可计算出不同置信度下形状参数和尺度参数的估计区间,对于α的估计区间[αL,αU],如式(10)~(11)所示:
(10)
(11)
式中:αL为形状参数的区间估计下限值;αU为形状参数的区间估计上限值。
对于β估计区间[βL,βU],如式(12)~(13)所示:
(12)
(13)
式中:βL为尺度参数区间估计下限值;βU为尺度参数区间估计上限值;d1和d2分别为中间系数。
对于d1和d2计算,如式(14)~(18)所示:
(14)
(15)
(16)
(17)
(18)
式中:A3,A4,A5和A6分别为区间估计的中间系数;x为标准正态分布的1-η分位点。
3 化工安全联锁设备的PFDavg算法和SIL验证
工程中为保证安全联锁系统在发生紧急情况时正常运行,定期执行设备的预防性维修计划(PM),在这个周期里进行1次检修和维护。记T0为设备的预防性维修周期,给出求解紧急放空执行单元PFDavg的3种算法[12]。
(19)
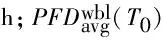
(20)
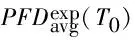
(21)

4 案例分析
以某蜡油加氢装置的典型安全联锁系统回路[13]的紧急放空阀(EDV)为例(注:视为1oo1结构,现场实际的EDV为1用1备)。该回路中,催化加氢反应器的顶部气相产物,经过热高压分离器分离的热高分气体进入热高分气换热至184 ℃,再经过热高分器空冷器A01001冷却至50 ℃后进入冷高压分离器。自冷高压分离器顶部出来的循环氢经脱硫塔入口分液罐分液后,进入D03001循环氢脱硫塔底部,紧急放空阀的联锁回路,如图2所示。
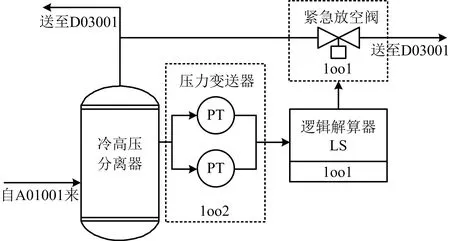
图2 紧急放空阀的联锁回路
该回路中,由压力变送器PT实时监测冷高压分离器内压力,并将数据传至逻辑解算器LS单元,当冷高压分离器内压强超过2.1 MPa时,由逻辑解算器LS提供触发信号给紧急放空阀,打开阀门以0.7 MPa/min的泄压速率将超压气体排出。
结合SIS失效数据库中紧急放空阀的失效统计数据[14],以及参考实际工程中服从威布尔分布的紧急放空阀失效参数,设置形状参数为1.49,尺度参数为6 025 003,通过蒙特卡洛仿真模拟生成200组随机失效数据。
根据加氢装置实际运行的情况,在得到模拟样本后,进行截尾时长为175 200 h的I型截尾处理,得到150组完整失效数据和50组截尾失效数据。需要强调的是,采用蒙特卡洛模拟的截尾失效数据作为测试数据,并不影响比较统计分析的有效性,且可以比实际的工程采集数据提供更客观的误差分析结果[15]。
使用试错法,先是试错α估计值区间的选取,考虑到设备运行周期内失效率是1个缓慢上升的过程,并查阅相关阀的失效参数库,得知α值在1.0至1.7范围内,因此试错值假设在该区间,依次带入式(4),求得α估计值偏差量,并求得似然估计求解的α和β估计值,如表1所示。

表1 似然估计求解α和β估计值
由表1计算得到的数据,绘制α估计值偏差量与β估计值双坐标曲线,如图3所示。
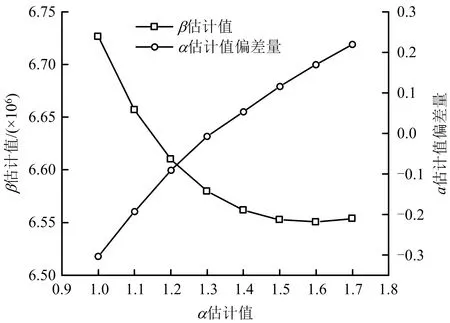
图3 α估计值偏差量与β估计值曲线
根据式(14)~(18),威布尔区间估计可算出70%置信度时d1=0.124,d2=-0.116,90%置信度时d1=0.198,d2=-0.198,代入式(12)~(13)中,算出β估计区间的上限值和下限值。

表2 威布尔分布和指数分布的参数估计区间
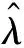
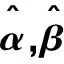
表3 70%和90%置信度时和估计值
分别在70%和90%这2种不同的参数估计置信度下,研究不同T0时,威布尔分布,指数分布和IEC61508的PFDavg计算结果的变化曲线,并分析这3种算法结果的差异。结合工程实际,为便于比较将安全联锁设备的T0分别取1,2,3,4,5 a。得到70%和90%置信度时3 种算法的PFDavg变化趋势。70%置信度下3种算法的PFDavg与T0关系,如图4所示;90%置信度下3种算法的PFDavg与T0关系,如图5所示。

图4 70%置信度下3种算法的PFDavg与T0的关系

图5 90%置信度下3种算法的PFDavg与T0的关系
由图4~5可知,70%和90%置信度下指数分布和IEC61508的PFDavg曲线差值均较小,证明IEC61508简化算法替代指数分布算法的合理性。
鉴于指数分布和IEC61508的2种算法的计算结果相差不大,因此将仅在70%和90%置信度时分析指数分布算法与威布尔分布算法的PFDavg计算值之间的相对误差和绝对误差,并进行对比。指数分布与威布尔分布PFDavg的相对误差分析,如图6所示;指数分布与威布尔分布PFDavg的绝对误差分析,如图7所示。
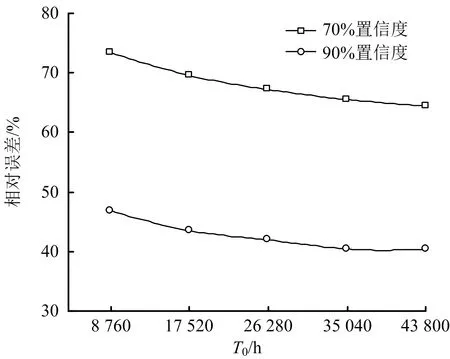
图6 指数分布与威布尔分布PFDavg的相对误差分析
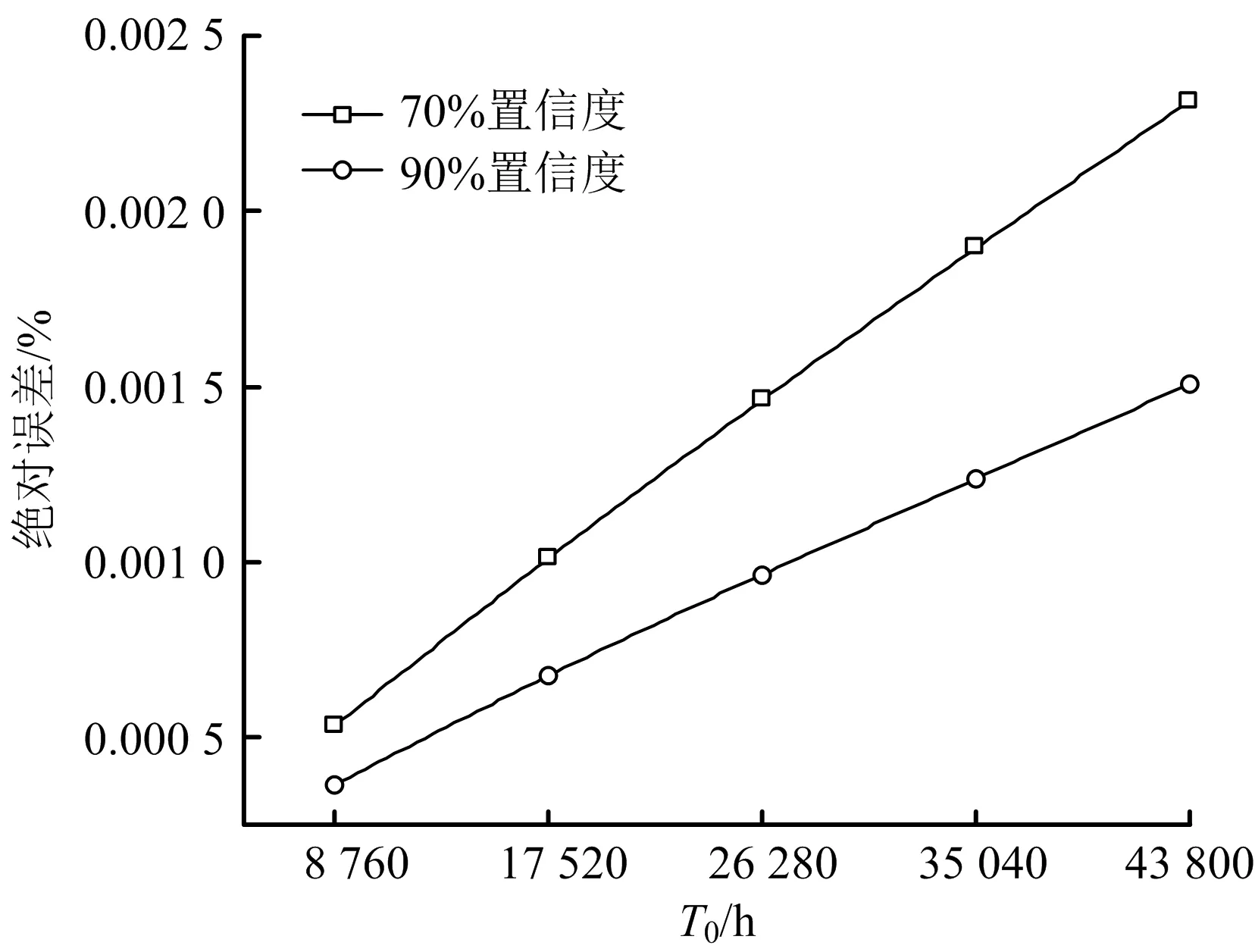
图7 指数分布与威布尔分布PFDavg的绝对误差分析
IEC61508算法的PFDavg值随着T0的增大,绝对误差(即IEC61508和指数分布PFDavg相比于威布尔分布PFDavg的数值偏差)增大,而相对误差值减小。绝对误差作为SIL验证中数值误差的直接表现,表明在指定预防性维修周期内存在较大误差,证明工程上寿命服从威布尔分布的设备,简化为采用指数分布算法计算其PFDavg的不合理性,并将导致显著的风险研判偏差。
指数分布和IEC61508算法的SIL验证结果基本一致,2者的验证结果不再区分考虑。根据IEC61508中对SIL验证的等级划分规则,得出70%置信度时2种PFDavg算法的SIL验证结果,如表4所示;90%置信度时2种PFDavg算法的SIL验证结果,如表5所示。
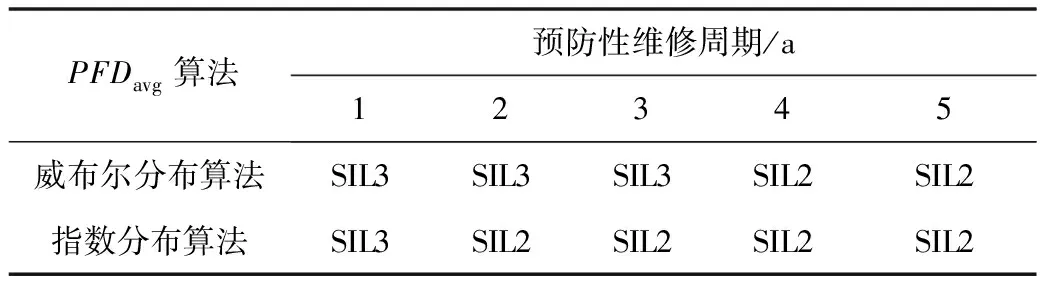
表4 70%置信度时2种PFDavg算法的SIL验证结果

表5 90%置信度时2种PFDavg算法的SIL验证结果
用模拟的方法得出,对于通过SIL验证等级为SIL2的设备,如果实际寿命服从威布尔分布,则实际SIL验证是有可能达到SIL3的。在表4~5中,预防性维修周期为1~3 a时,由威布尔分布算法得到的SIL验证结果普遍比指数分布和IEC61508算法的SIL验证结果高1个等级,可见服从威布尔分布的设备在使用IEC61508算法进行计算时将存在相当大的偏差,导致化工企业SIS升级改造项目投资过大。70%与90%置信度下的威布尔分布算法的SIL验证结果存在一定差异,考虑到高置信度下计算得到的PFDavg值高于低置信度计算PFDavg值,在PFDavg数值计算使用70%置信度,结果较为折中,而使用90%置信度结果较为保守,验证了IEC61508中,PFDavg算法推荐置信度为70%,数据采集和处理推荐置信度为90%的这一建议基本合理。
5 结论
1)对于联锁回路的执行单元等容易发生机械疲劳磨损的设备,其失效率在使用过程中缓慢上升,因此宜使用威布尔分布对设备失效时间数据进行分析和PFDavg计算;此外本文案例虽考虑的是1oo1结构,整个计算流程亦适用于其他表决结构。
2)如果对于寿命服从威布尔分布的设备,使用IEC61508算法计算的PFDavg可能会造成SIL验证的误差,低估了设备可以达到的SIL级别,造成化工厂的SIS改造投资增大。
3)区间估计的置信度越高,IEC61508算法计算的PFDavg与实际PFDavg偏差越小。随着预防性维修周期的延长,在相同置信度下IEC61508的PFDavg与实际PFDavg间的相对误差减小,绝对误差增大。因此化工企业的允许短周期维护的联锁回路策略,采用IEC61508以及高置信度参数估计的验证结果基本可信。
