考虑随机误差的软土基坑沉降趋势分析及预测*

苗兰弟，任庆国

(陕西铁路工程职业技术学院，陕西 渭南 714000)

0 引言

为满足市政经济建设需求，地下空间工程开发日益发达，尤其是市政轨道工程建设。建设过程产生大量车站基坑，受施工条件限制，软土地区基坑施工不可避免，但软土地区土体工程性质较差，需对软土地区基坑变形规律展开研究[1-3]。沉降监测是基坑施工变形监测必测项目，相关学者针对沉降监测开展研究：姚文龙等[4]对基坑施工过程地表沉降进行理论计算；王灿等[5]利用数值模拟分析基坑近接施工过程中地表沉降规律；基于文献[6-7]研究成果得出，基坑变形数据误差信息会影响基坑沉降规律，需对误差信息分解处理；王成等[8]通过研究得出卡尔曼滤波具有较强误差分解能力，应用于基坑误差信息分解可行；王雪妮等[9]验证M-K检验在基坑变形趋势判断中适用性；钟国强等[10]验证广义回归神经网络在基坑变形预测中有效性。上述研究虽取得一定成果，但研究方法单一，且未考虑随机误差影响，缺乏系统性。因此，本文以苏州4号线活力岛站基坑为工程背景，利用卡尔曼滤波分解基坑沉降数据趋势项与误差项，采用M-K检验、优化广义回归神经网络和差分整合移动平均自回归模型开展基坑沉降趋势分析及预测，以期合理掌握基坑沉降变形规律，为安全施工提供理论指导。

1 基本原理

基坑沉降监测受环境因素、人为因素扰动，变形数据存在一定误差，使基坑沉降实测值分解为2项，即趋势项和误差项。其中，趋势项代表基坑沉降真实信息，误差项代表不确定因素造成随机误差。

为准确掌握基坑沉降变形规律，利用卡尔曼滤波法对趋势项与误差项进行分解处理。基坑沉降变形规律研究包括2个阶段：阶段Ⅰ利用M-K检验进行趋势项发展趋势评价；阶段Ⅱ利用优化广义回归神经网络(Generalized Regression Neural Network，GRNN)和差分整合移动平均自回归模型(Arima)进行基坑沉降变形预测。通过对2个阶段结果进行对比，实现基坑沉降变形规律综合研究。

1.1 信息分解处理模型构建

卡尔曼滤波系统状态下最优估计算法，相较于传统小波去噪具有一定优越性，但受传统理论基础限制，标准型卡尔曼滤波存在发散强、抵抗力差等缺点。为此得到改进型卡尔曼滤波法，主要包括自适应型、抗差自适应型和半参数型3种。

为保证基坑沉降数据信息分解效果，将分析过程分为2个步骤：将标准型卡尔曼滤波与传统sym、cof小波进行分解效果对比，且传统sym、cof小波阶次设定为3、5、7、9阶；对比4类卡尔曼滤波分解效果，确定最优分解类型。

信息分解效果评价常用指标包括信噪比、均方根误差等，鉴于不同评价指标原理差异，基于信噪比及均方根误差指标，构建综合评价指标l(k)如式(1)所示：

l(k)=l1(k)+l2(k)

(1)

式中：l1(k)、l2(k)分别为信噪比及均方根误差指标归一化值，l(k)值越大，分解效果相对越好；k为分解方法序号。

归一化处理能有效避免不同评价指标单位差异影响。

1.2 发展趋势分析模型构建

Manner-Kendall检验法(简称：M-K检验)是1种非参数统计方法，操作简单、准确性高，可有效实现变形趋势判断分析，在基坑工程中应用广泛。基坑沉降数据误差信息会影响分析结果，因此，仅采用M-K检验对趋势项进行发展趋势评价。

M-K检验过程得到初步统计量S，如式(2)所示：

(2)

式中：Xi，Xj分别为时间节点i与j沉降值；sgn(θ)为反应函数(当θ<0时，sgn(θ)为-1；当θ>0时，sgn(θ)为1；当θ=0时，sgn(θ)为0)。

对S进行变换处理，得到M-K检验最终统计量Z，如式(3)所示：

(3)

式中：Var(S)=[n(n+1)(2n+5)]/18；n为样本总数。

在检验水平a条件下得到对应临界值Za，若Za0时，基坑沉降呈增加趋势；反之，基坑沉降呈减小趋势。

同时，由于临界值Za与临界水平a相关，即检验水平a越低，临界值Za越大，可利用检验水平划分基坑沉降变形显著性等级，具体基坑沉降趋势等级划分标准见表1。

表1 基坑沉降趋势等级划分标准

1.3 沉降预测模型构建

基坑沉降变形数据分为趋势项和误差项，2者信息存在一定差异。构建相应预测模型，首先利用优化GRNN模型实现主趋势项预测，再利用Arima模型实现残差修正预测，具体包括以下2个过程：

1)主趋势项预测模型构建

GRNN模型是传统径向基神经网络改进形式，理论基础更加完善，具有较强非线性预测能力，适用于基坑沉降主趋势项预测；同时，该模型相较于传统神经网络模型，具有4层网络结构，新增加和层加快收敛速度。

但GRNN模型因收敛较快，易陷入局部极值。果蝇算法(Fruit Fly Optimization Algorithm,FOA)是1种常用优化算法，全局优化能力较强，可有效优化GRNN模型。传统FOA算法优化步长为定值，步长过大，局部搜索能力变弱；反之，全局优化不足，多种群果蝇算法(MFOA)可有效克服上述问题。因此，本文利用MFOA算法对GRNN模型进行优化，构建基坑沉降变形主趋势项MFOA-GRNN预测模型。

2)残差序列修正预测模型构建

MFOA-GRNN预测模型保证模型参数最优性，但受沉降数据非线性限制，难以全面刻画基坑沉降变形主趋势项变形规律，预测结果存在误差。将该预测误差与卡尔曼滤波分解出误差项组合，构成基坑沉降变形残差序列；为保证沉降预测精度，利用Arima模型进行残差修正预测。

将Arima模型残差修正结果与MFOA-GRNN模型主趋势项预测结果叠加，即基坑沉降最终预测结果。

预测过程中，利用预测结果相对误差均值与训练时间进行预测效果评价，前者主要用于评价预测精度，后者主要用于评价收敛速度。

2 实例分析

2.1 工程概况

活力岛站隶属苏州地铁4号线，位于春申湖南侧，近似沿文灵路展布；基坑外包长度199.6 m，外包宽度19.7 m，标准段开挖深度16 m，端头加深段开挖深度18.5 m；同时，该基坑采用地下连续墙支护，并设置5道横撑，开挖方量达6.4万m3。

勘察结果显示，工程区为冲积湖平原地貌，地势相对平坦，地面标高介于2.72～4.02 m；基坑开挖范围内主要涉及4类土层。

工程区内地表水以文灵河为主，其余为地表水网，受降雨影响较大。地下水埋深1.3～2.3 m，主要包括潜水、微承压水和承压水，其中潜水主要分布于土层孔隙中，年变幅约1 m，历史最高、最低水位分别为2.63，0.21 m；微承压水主要赋存于④1粉黏夹粉土中，水头标高约1 m，对施工影响较大；承压水赋存于坑底下部土层，埋深大于30 m，对施工影响较小。

2.2 沉降变形特征分析

由于工程区开挖范围土体具软土特征，为保证施工安全，在基坑施工过程中，进行变形监测。其中，沉降监测为必测项。在活力岛站基坑施工过程中，共布设26组沉降监测，每组含3个监测点，按基坑边垂向布设，距基坑支护结构距离分别为0，2，7 m(序号依次为1#、2#和3#)，基坑沉降监测点布置如图1所示。

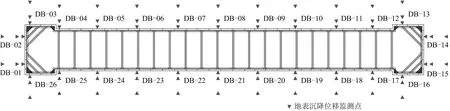
图1 基坑沉降监测点布置

一般距基坑工程越近受扰动越大。对监测点1#沉降变形分布进行统计，如图2所示。由图2可知，基坑沉降变形具明显波状起伏，分别计算北侧、南侧、东侧及西侧沉降均值分别为13.50,14.05,16.78,17.15 mm；结合沉降监测点布设情况可知，基坑短边向沉降变形相对偏小，长边向中部沉降变形相对偏大，原因是基坑短边或拐角处支护结构刚度相对较大，长边中部处结构刚度相对较小。

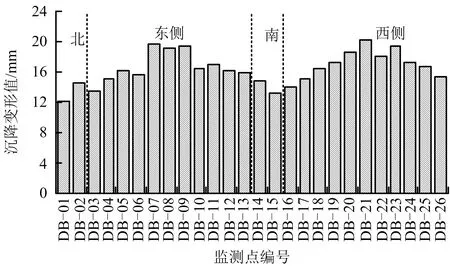
图2 1#监测点沉降变形分布

为分析沿基坑边垂向沉降分布特征，选取沉降变形较大的4个监测点(DB-07、DB-09、DB-21和DB-23)进行统计，基坑垂向沉降分布特征如图3所示。

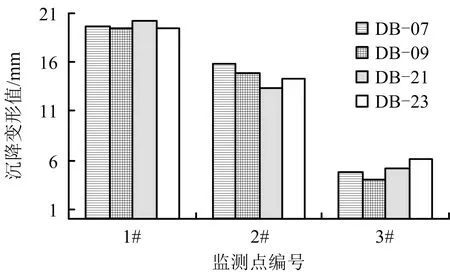
图3 基坑垂向沉降分布特征

由图3可知，随距支护结构距离增加，沉降变形逐渐减小，且2#监测点与1#监测点沉降变形差值明显小于3#监测点与2#监测点沉降变形差值。因此，建议基坑施工期间，应与周边临近建/构筑物保持安全距离。

在沉降监测过程中，监测频率为2 d/次，共27个周期沉降监测成果，基坑沉降变形曲线如图4所示。由图4可知，4个监测点沉降变形呈持续上升趋势。

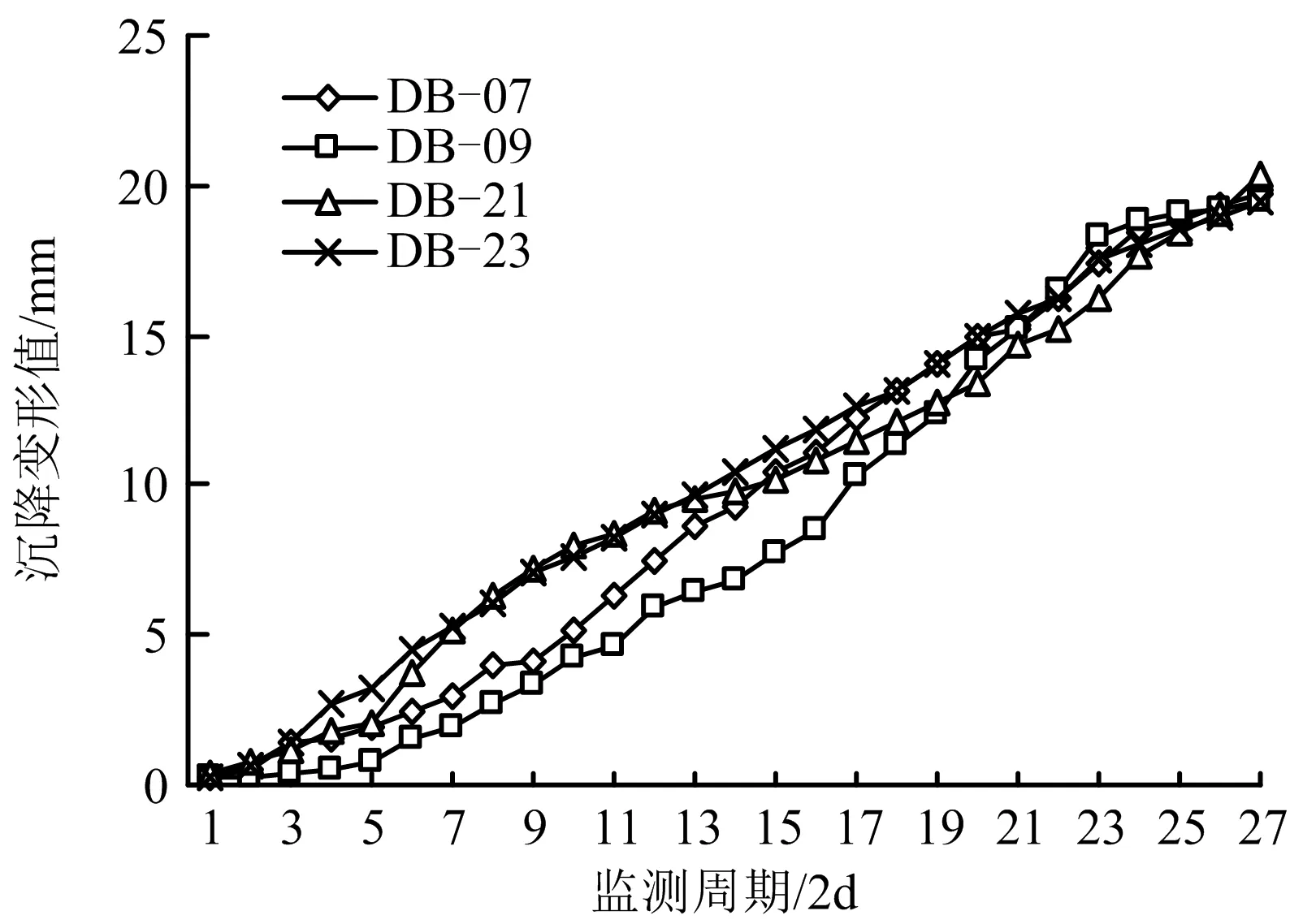
图4 基坑沉降变形曲线

2.3 变形数据信息分解处理

以DB-07监测点为例，进行卡尔曼滤波分解效果验证。将标准型卡尔曼滤波与传统小波分解效果对比分析，结果见表2。

由表2可知，传统小波阶次对分解效果影响较明显，随小波阶次增加，分解效果逐渐变好。通过对比3类方法分解效果可知，卡尔曼滤波评价指标值最大为1.836，其次为cof小波和sym小波，说明卡尔曼滤波相对传统小波信息分解效果更好。

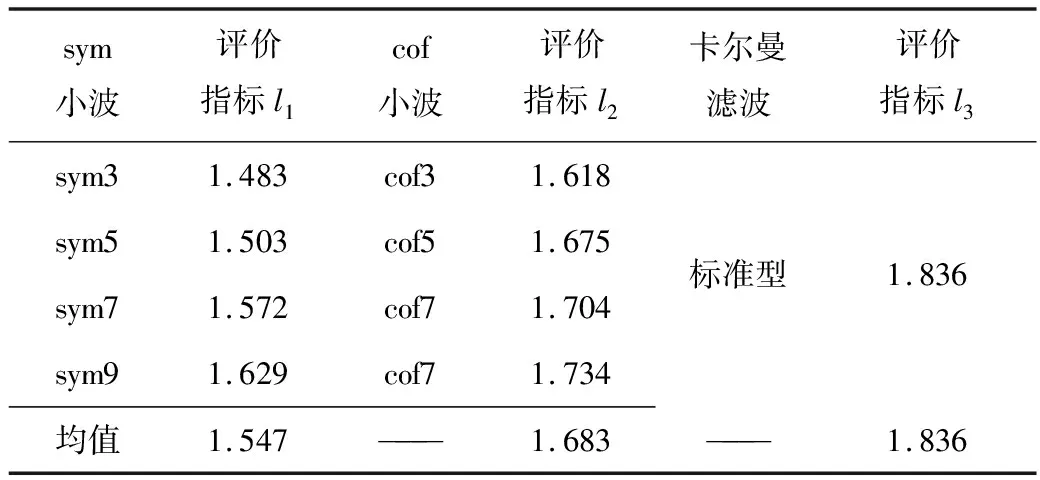
表2 卡尔曼滤波与传统小波的分解效果对比

对多种改良型卡尔曼滤波信息分解效果对比，结果见表3。由表3可知，不同类型卡尔曼滤波分解效果差异明显，3种改良型分解能力优于标准型，且半参数型分解效果相对最优，其次是自适应型和抗差自适应型。

表3 不同类型卡尔曼滤波的分解效果对比

综上，半参数型卡尔曼滤波信息分解能力相对最优，将其作为基坑沉降数据信息分解方法切实可行。

2.4 沉降变形发展趋势分析

利用M-K检验对基坑沉降变形趋势项发展趋势分析。分析过程包含整体趋势分析和分阶段趋势分析。其中，整体趋势分析是对所有监测数据进行M-K检验，以评价基坑整体发展趋势；分阶段趋势分析将监测成果分为3个阶段(每阶段递增9期监测成果)，并对每阶段进行M-K检验，以评价基坑沉降不同阶段发展趋势。

1)整体趋势分析。对4个监测点整体趋势进行分析，结果见表4。由表4可知，不同监测点Z值存在一定差异，表明沉降趋势性不同。其中，DB-07和DB-23监测点显著性等级为Ⅱ级，显著性程度属显著；DB-09和DB-21监测点显著性等级为Ⅰ级，显著性程度属弱显著。4个监测点显著性等级虽存在一定差异，但发展趋势均呈增加趋势，说明整体分析条件下，基坑沉降仍会进一步增加。

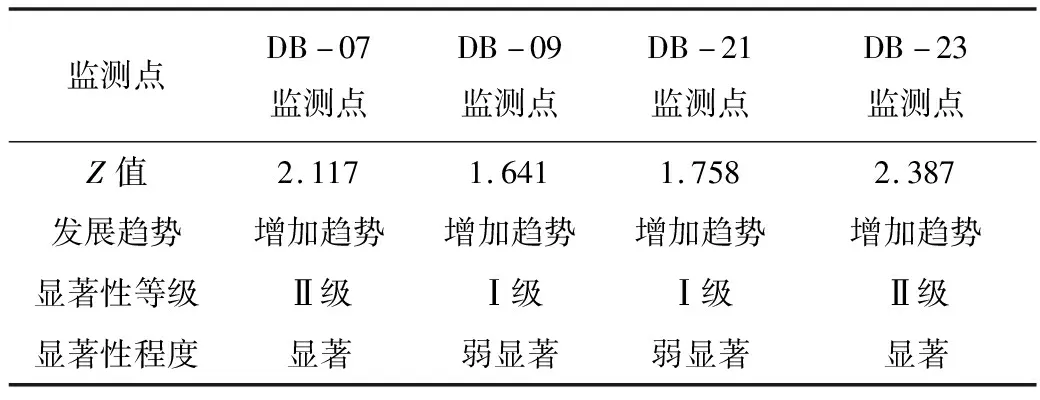
表4 基坑沉降的整体趋势分析结果

2)分阶段趋势分析。4个监测点分阶段趋势分析结果见表5。由表5可知，不同阶段显著性等级存在差异：阶段2显著性等级相对最高，即随监测时间增加，基坑沉降显著性呈先增加后减小趋势。

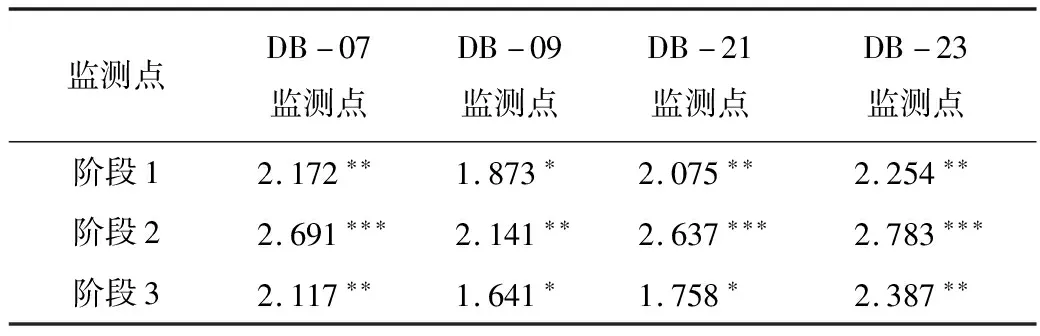
表5 基坑沉降分阶段趋势分析结果

综上可知，活力岛站基坑沉降仍具增加趋势，但趋势性相对减弱。

2.5 沉降变形预测分析

以DB-07监测点为例，描述不同优化阶段预测效果，实现预测思路初步验证；利用其余3个监测点预测结果，实现预测思路可靠性验证。预测过程中，以1～22周期为训练样本，23～27周期为验证样本，外推预测周期为4期。

1)初步验证分析。利用果蝇算法优化GRNN模型，并将FOA算法和MFOA算法优化结果进行统计，结果见表6。由表6可知，在验证节点处，MFOA-GRNN模型相对误差值均不同程度小于FOA-GRNN模型相对误差值，MFOA-GRNN模型相对误差均值和训练时间分别为2.13%和42.21 ms，FOA-GRNN模型相对误差均值和训练时间分别为2.47%和47.39 ms，说明MFOA算法预测精度更高，收敛速度更快，验证MFOA算法优越性。据MFOA-GRNN模型预测误差均值仅为2.13%，验证趋势项预测思路有效性，且训练时间相较于优化前略有增加，但影响不大，属可接受范围。

表6 DB-07监测点的趋势项预测结果

利用Arima模型进行残差修正，DB-07监测点最终预测结果见表7。由表7可知，通过残差修正预测，DB-07监测点最大、最小相对误差分别为2.03%和1.68%，平均相对误差为1.80%，较残差修正前有明显提高，验证Arima模型残差修正能力；通过Arima模型残差修正增加一定训练时间，但仅为53.18 ms，属可接受范围。在外推预测结果中，DB-07监测点沉降变形仍会进一步增加，但增加速率较小。

表7 DB-07监测点最终预测结果

2)可靠性验证分析。其余3个监测点可靠性预测结果见表8。由表8可知，3个验证监测点平均相对误差间于1.80%～1.90%，与DB-07监测点预测精度基本一致，说明本文预测模型具有较强稳定性，且训练时间均小于60 ms，属可接受范围。

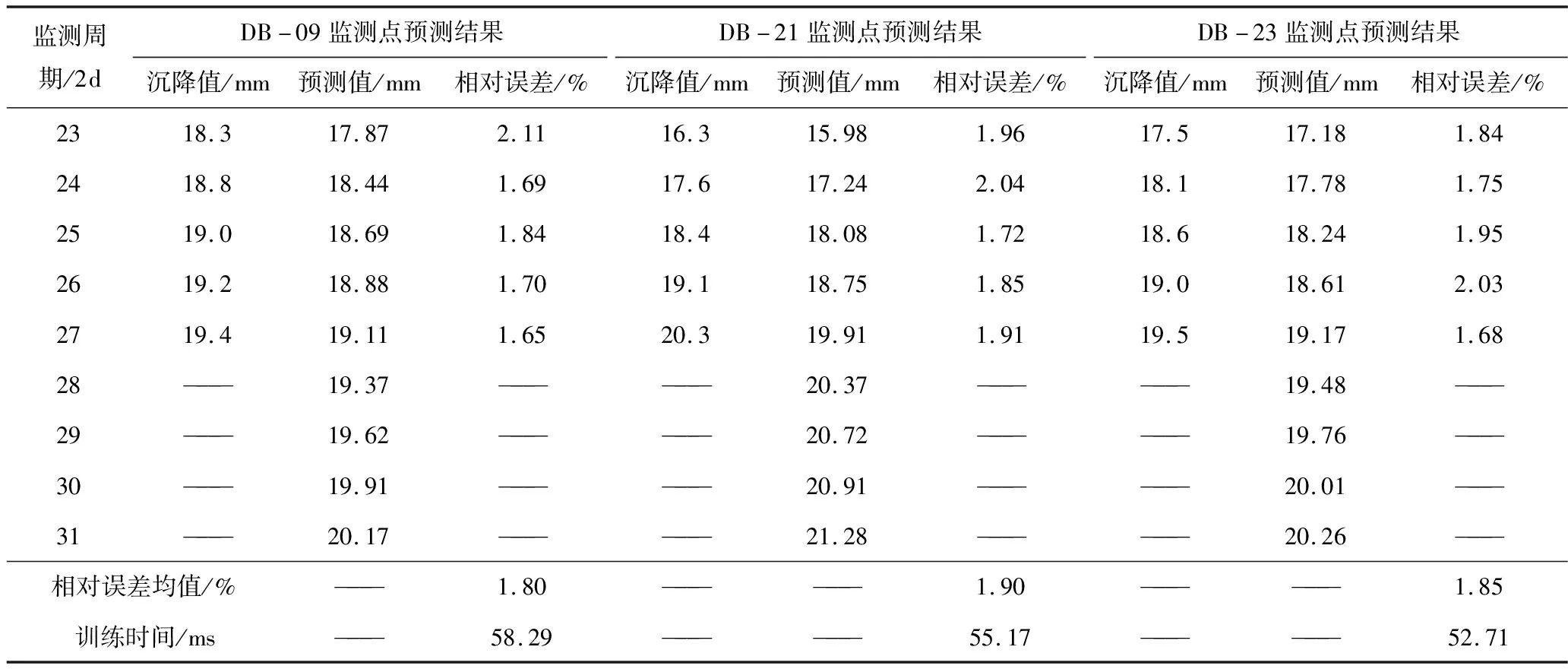
表8 可靠性验证预测结果

对比3个监测点外推预测结果可知，3者沉降变形均会进一步增加，但增加速率均明显降低，与DB-07监测点外推预测结果一致，充分说明本文通过预测得出沉降趋势判断结果准确性较高。

3 结论

1)基坑沉降变形数据含有一定误差信息，给变形规律研究带来一定影响；相较传统小波，卡尔曼滤波对趋势项及误差项分解效果更佳。

2)M-K检验能准确实现基坑沉降趋势分析，随监测时间增加，基坑沉降呈持续增加趋势，但显著性呈先增加后减小趋势，基坑沉降增加趋势逐渐减弱。

3)沉降预测模型构建过程中，对模型参数进行优化处理，保证参数最优性。本文预测思路精度较高，平均相对误差均小于2%，验证预测思路在基坑沉降预测中有效性；由外推预测可知，沉降变形会进一步增加，但增加速率明显降低，与发展趋势分析结果一致。