考虑滚动阻抗的线性接触模型离散元宏细观参数敏感性研究*

马少坤,黄 骁,韦榕宽,刘 莹,段智博

(1.广西大学 土木建筑工程学院，广西 南宁 530004;2.广西大学 工程防灾与结构安全重点实验室，广西 南宁 530004)

0 引言

岩土体作为1种天然的工程材料，其复杂的工程特性在生产实践中常常引发不可预知的安全事故，例如边坡失稳[1]、隧道塌方[2]等。而Cundall于20世纪70年代提出的离散元法为研究岩土的相关特性提供1种有效手段[3]，对工程安全具有重要意义。离散元法的核心接触模型区别于传统土力学理论中的宏观本构模型，主要由颗粒与颗粒间的细观接触特性及参数所表征[3-4]。然而在实际工程和试验中所测得岩土体的变形或强度特性均以宏观参数来体现，这使得在利用离散元法对土体进行仿真模拟时，选取与其匹配的接触模型及细观参数较困难。

大量学者针对接触模型细观参数与土体宏观力学参数的关系进行定量研究。曾远等[5]利用PFC2D离散元分析软件，进行多组无黏性土双轴模拟试验，详细分析细观参数对土体宏观特性的影响;陈亚东等[6]建立多组不同细观参数的模拟真三轴数值试验，分析无黏性土细观参数与宏观参数的关系，并提出针对无黏性土的细观参数确定方法；徐小敏等[7]开展一系列基于线性接触模型的模拟试验，分析颗粒细观参数与试样宏观参数的关系，并建立经验公式。上述基于无黏性土的细观参数研究均以“ball”为基础单元，鲜有考虑真实土颗粒的形状效应，即忽略土颗粒之间的抗转动作用；而Iwashita等[8]通过试验发现颗粒间的抗转动作用对颗粒的力学性质有显著的影响。因此，部分学者也对抗转动模型进行研究[9]。

此外，为探讨宏细观参数间的非线性关系，利用计算机算法对模拟数据进行分析。周喻等[10]采用BP神经网络方法对400 组细观力学参数随机组合的三轴模拟试验数据建立宏观力学参数与细观力学参数的非线性模型，结果表明此模型可快速、准确地反演岩土体的非线性关系；李澄清等[11]利用25组双轴压缩离散元数值试验模拟结果建立BP人工神经网络反演系统，结果表明模型反演性能较好；崔洋洋[12]开展多组基于线性接触模型的双轴压缩试验，利用BP人工神经网络分析方法寻找宏-细观参数之间的映射关系。

综上所述，本文基于抗转动线性接触模型，采用控制变量法开展一系列三轴试验数值分析，通过对比不同细观参数下的模拟试验结果，研究模型的不同细观参数对宏观参数的影响；针对对比试验无法体现出参数交互作用这一难题，引入随机森林机器学习法，详细探究宏细观参数的权重关系。

1 模型验证及结果

1.1 计算参数选取

为研究模型细观参数的敏感性，基于已有试验数据开展相应的数值试验以获得1组合理的土体基本细观参数。基于文献[13]，选取丰浦砂为模拟对象，选取相关计算参数，见表1。

表1 计算参数

此外，采用扩大颗粒粒径的方法保证计算效率。通过多次试算，最终选取由3 018个颗粒组成的试样，该数量足以反应材料特性[7],级配曲线对比如图1所示。最终标定结果见表2。

图1 原始级配与模拟级配曲线

表2 丰浦砂标定参数

1.2 模拟结果

丰浦砂三轴固结排水压缩室内试验与数值试验的结果对比如图2～3所示。由图2～3可知，在试验初期，式样的总体积减小，而偏应力-轴应变曲线近似为直线。随着试验不断进行，试样出现剪胀的趋势，而偏应力的增长不断放缓，直至到达峰值后，偏应力逐渐下降。总体而言，模拟结果与室内试验的结果契合度均较好，整体误差较小，证明利用该组细观参数可较好地表征丰浦砂。

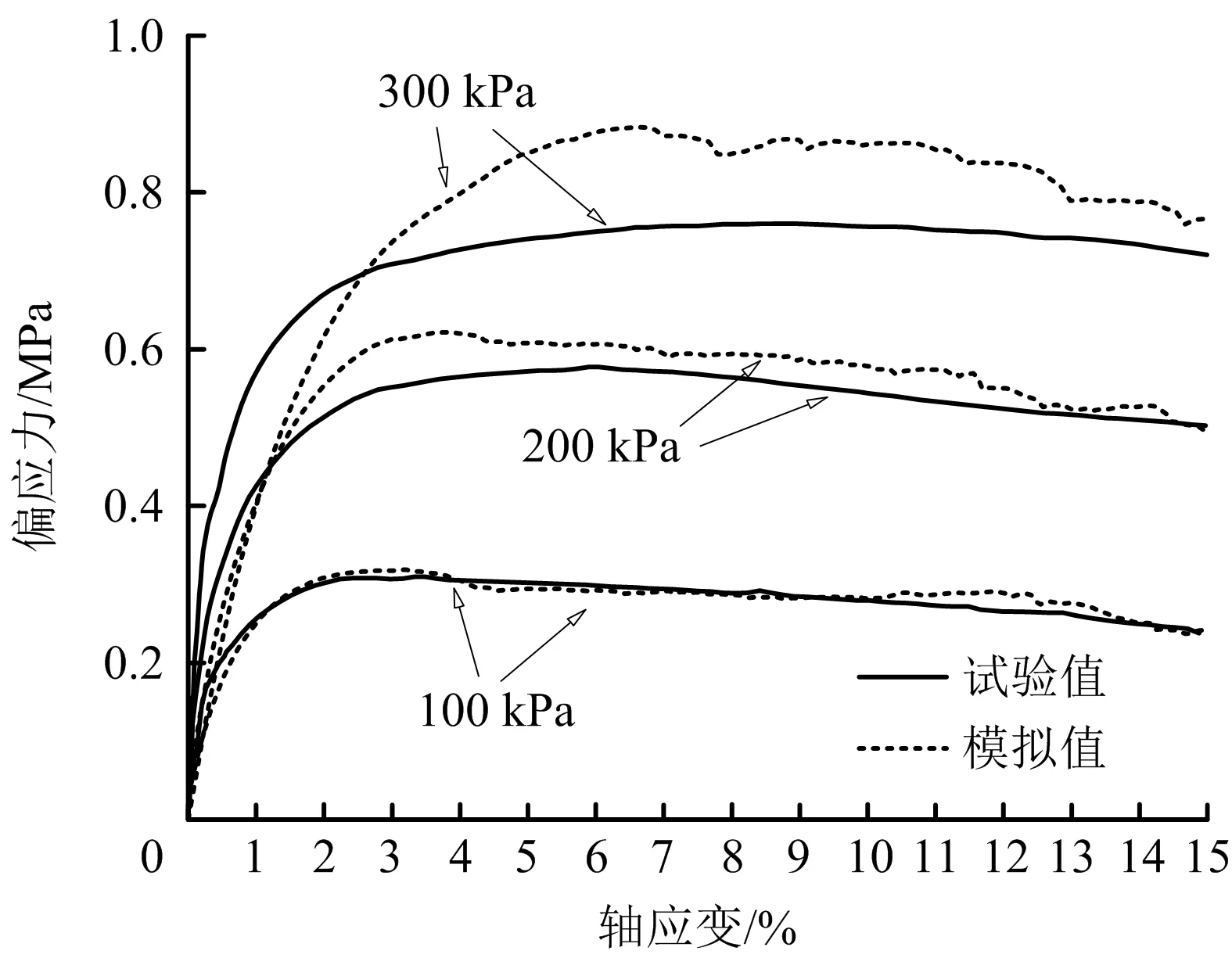
图2 丰浦砂室内试验与数值试验偏应力-轴应变曲线对比

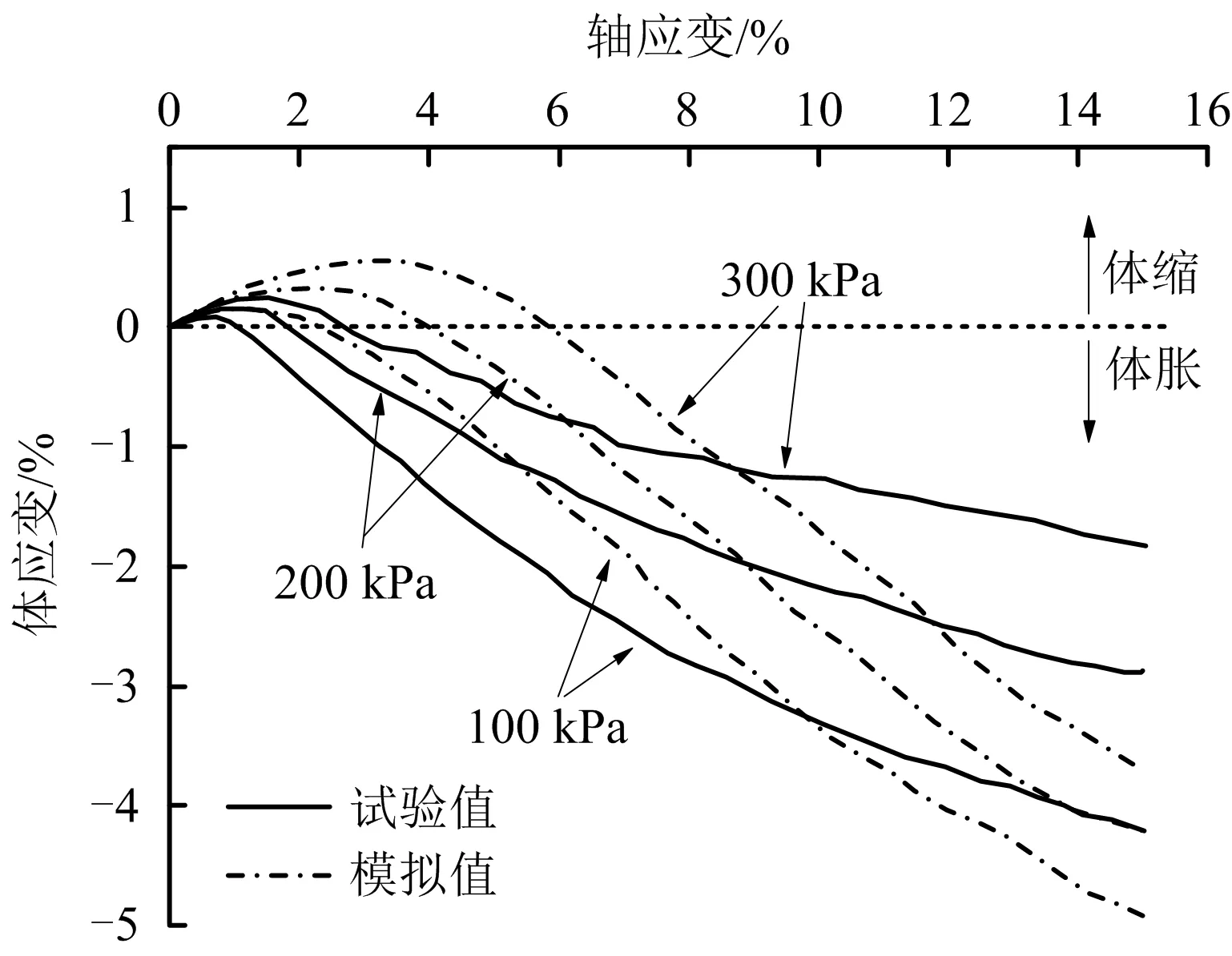
图3 丰浦砂室内试验与数值试验的体应变-轴应变曲线对比

2 参数敏感性分析

在土体参数标定中，将土体宏观参数(包括初始弹性模量、泊松比、峰值强度等)与模型细观参数相对应。根据徐小敏等[7]的研究，在离散元三轴模拟试验中，当试样的轴向应变处于峰值应力所对应轴向应变的1%范围内时，可视为试样处于弹性形变阶段。可根据此范围内的偏应力-轴应变曲线与体应变-轴应变曲线计算出试样所对应的初始弹性模量与泊松比，如式(1)～(2)所示：

(1)

(2)

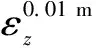
为研究和表征出各个细观参数对宏观参数的影响，基于本文所得丰浦砂对应的模型参数，为各个细观参数设计进行对比试验，模拟试验方案见表3。

表3 模拟试验方案

2.1 有效模量的影响

有效模量会显著影响试样的初始弹性模量。不同围压下有效模量与试样初始弹性模量的变化规律如图4所示。由图4可知，二者呈正相关关系。即试样的初始弹性模量随着有效模量的增大而增大。这是因为当颗粒间有效模量增大时，颗粒间法向刚度与切向刚度随之增大，而三轴试验中上下加载板的加载速率保持恒定不变，因此在试样加载过程中，颗粒间的变形等速率增加，而颗粒间法向刚度与切向刚度增大导致其接触力变大，故在试样处于较小的且相同的轴应变时，有效模量越大的试样的轴应力越大，从而在宏观上体现为颗粒间有效模量的增加会显著增大试样的初始弹性模量。

图4 不同围压下初始弹性模量随有效模量变化规律曲线

此外，有效模量的变化还会对试样的泊松比产生影响。不同围压下泊松比随有效模量变化规律曲线如图5所示。由图5可知，泊松比会随着有效模量的增大而增大。这是因为当颗粒间有效模量增大时，颗粒间法向刚度和切向刚度随之增大，而试样处于轴向加载速率不变的条件下，颗粒间的径向合力会增大，此时伺服侧壁需要更大的径向位移以保证围压的恒定，在宏观参数上表现为泊松比随之增大。

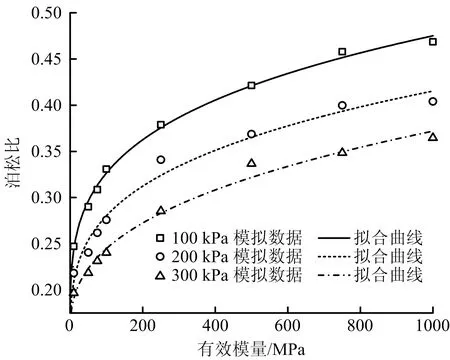
图5 不同围压下泊松比随有效模量变化规律曲线

2.2 刚度比的影响

刚度比的变化会显著影响土体初始抗变形能力。不同围压下泊松比随刚度比变化关系曲线如图6所示。由图6可知，试样的泊松比随刚度比的增大而增大。这是因为当颗粒的有效模量不变时，刚度比的增大使得颗粒间的切向刚度不断减小，剪切带内部颗粒可提供的接触力径向合力不足以与围压保持平衡。因此试样内部需调动更大范围的颗粒来平衡外部围压，造成更大范围内颗粒的相对滑移，从而使试样产生更大的径向变形。因此刚度比的增大会导致试样整体的切向抗变形能力下降，在宏观参数上反映为泊松比随刚度比的增大而增大。

图6 不同围压下泊松比随刚度比变化关系曲线

此外，刚度比还对试样的初始弹性模量产生影响。不同围压下初始弹性模量随刚度比变化关系曲线如图7所示。由图7可知，初始弹性模量会随着刚度比的增大而不断减小，并最终趋于稳定。这是因为当刚度比较小时，试样具有较高的切向抗变形能力，剪切带内颗粒可保证在较小的相对位移下提供与侧向围压保持平衡的力，此时试样总体积减小，内部颗粒重叠量增大，轴向应力较高，从而具有较高的初始弹性模量；而随着刚度比的增加，其切向抗变形能力急剧下降，使得试样内部调动更多的颗粒相对移动以保持与侧向围压的平衡，导致在试验初期产生较大侧向变形。试样总体积增加，内部颗粒重叠量变小，轴向应力下降，从而造成初始弹性模量下降。而当颗粒的切向刚度减小到一定程度时，试样已完全调动内部颗粒以抵挡外部荷载，此时继续增加刚度比对初始弹性模量影响不大，因此在曲线上体现为初始弹性模量随着刚度比的增大而趋于定值。

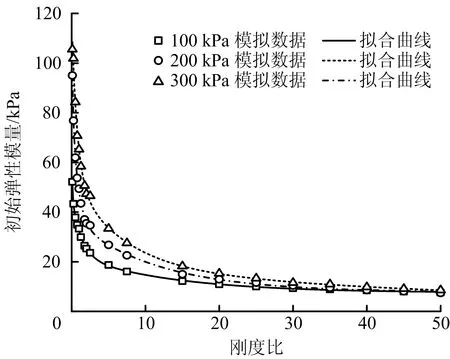
图7 不同围压下初始弹性模量随刚度比变化关系曲线

2.3 摩擦系数的影响

摩擦系数主要对土体的强度产生影响。因3种不同围压条件下，不同摩擦系数下的偏应力-轴应变关系曲线的规律相似，此处选取100 kPa为例进行分析，规律曲线如图8所示，其中μ为摩擦系数。由图8可知，摩擦系数与峰值强度呈正相关，而残余强度会随着摩擦系数的增大而趋于定值。

图8 100 kPa围压时不同摩擦系数下的偏应力-轴应变关系曲线

随着摩擦系数的增加，偏应力-轴应变曲线的变化可大致分为2个阶段。当摩擦系数较小时，土体偏应力-轴应变曲线整体呈现出“松砂型”的应变硬化趋势。而当摩擦系数较大时，偏应力-轴应变曲线呈现出“密砂型”的应变软化趋势。显然，试样的细观摩擦系数和所模拟土的宏观密实度之间存在相关性，即在同一粒径分布下，细观摩擦系数与土体的宏观压实度存在一定关系，这与文献[14]类似。

为考察摩擦系数对试样黏聚力的影响，绘制不同摩擦系数下强度包线及内摩擦角关系图，如图9所示。由图9可知，随着摩擦系数的增大，试样的内摩擦角显著增大，而增长速率随之减小；而从强度包线明显看出，摩擦系数的增加不会使试样产生黏聚力。

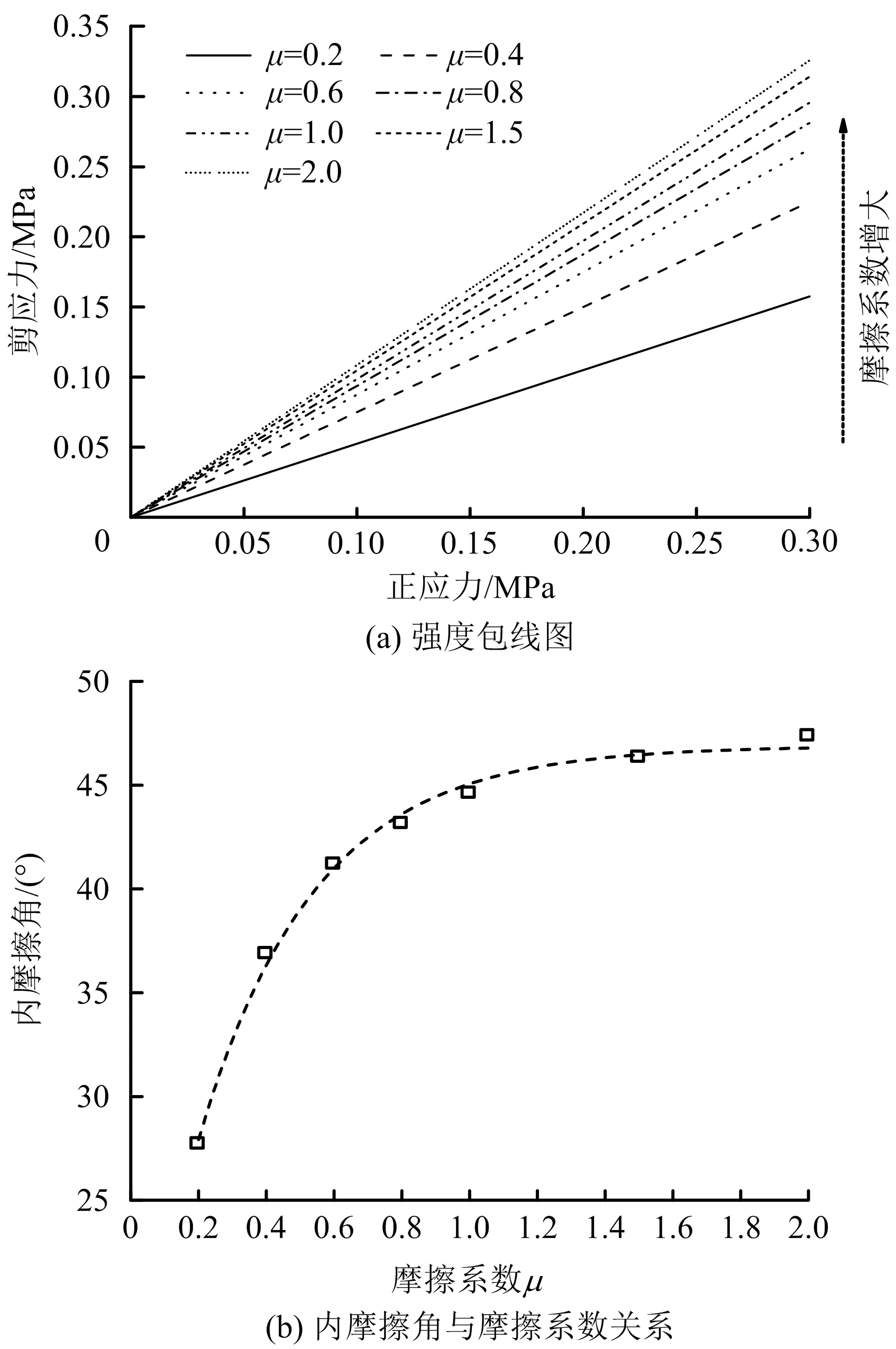
图9 摩擦系数对强度包线及内摩擦角的影响

2.4 抗转动系数的影响

抗转动系数会显著影响土体的抗剪强度。因3种不同围压条件下，不同抗转动系数下的偏应力-轴应变关系曲线的规律相似，此处选取100 Pka为例进行分析，100 kPa围压时不同抗转动系数下的偏应力-轴应变关系曲线如图10所示，其中，μr为抗转动系数。通过对模拟结果进行对比与分析，发现抗转动系数的取值存在作用区间，在此区间内，试样的峰值强度和残余强度均会随着系数的增大而增大，呈现出整体上升的趋势。当抗转动系数接近阈值时，土体偏应力-轴应变曲线基本不发生变化。其主要原因是当抗转动系数较大时，颗粒间临界转动阻力矩较大，此时试样中的颗粒间的相对转动矩未达到临界转动阻力矩，导致颗粒间发生的相对转动较小，宏观上表现为试样强度和变形参数几乎不随之变化。

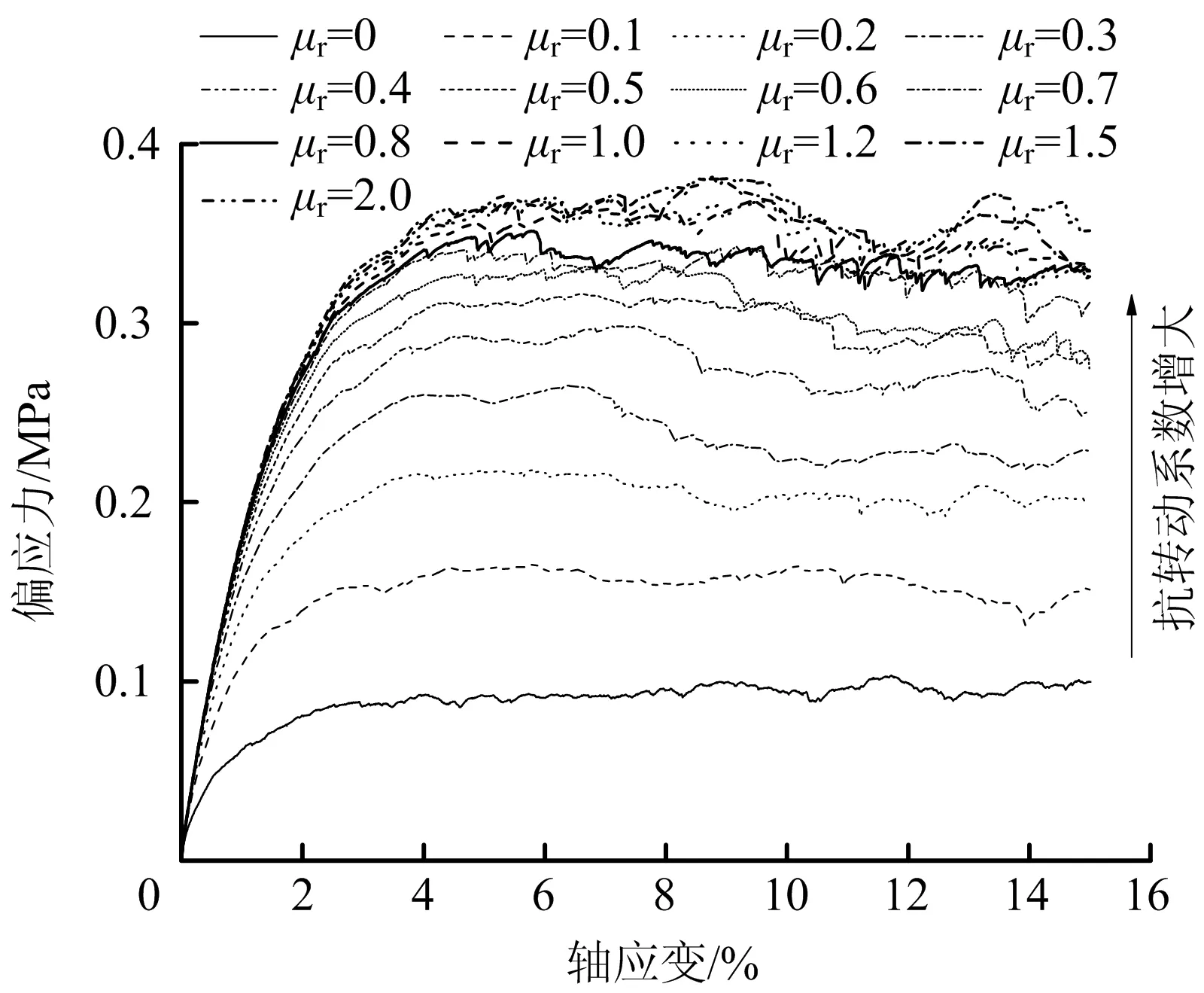
图10 100 kPa围压时不同抗转动系数下偏应力-轴应变关系曲线

为考察抗转动系数对试样黏聚力的影响，绘制不同抗转动系数下强度包线与内摩擦角关系图，如图11所示。由图11可知，抗转动系数不会使试样产生黏聚力，进一步验证抗转动模型对无黏性土的适用性。

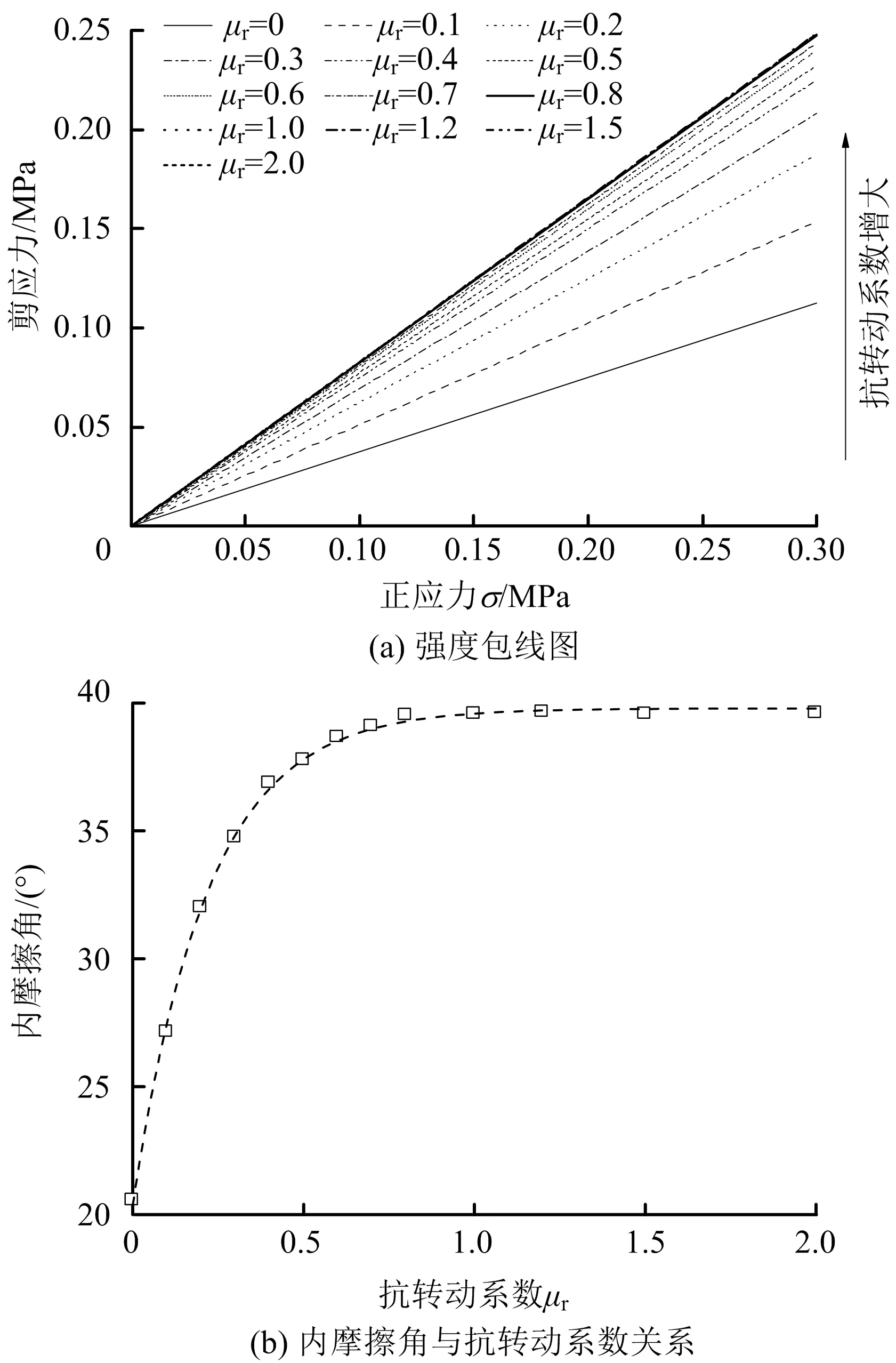
图11 抗转动系数对强度包线及内摩擦角的影响

此外，抗转动系数也对试样的剪胀性有显著影响。不同抗转动系数下试样的体应变-轴应变变化曲线如图12所示。由图12可知，随着抗转动系数的增大，试样的体应变在加载初期的弹性阶段并未产生较大的变化，即泊松比不被抗转动系数所影响。而随着加载不断进行，曲线发生分化，抗转动系数越大的试样剪胀趋势越强，且当抗转动系数接近阈值时趋于稳定，也进一步证明抗转动系数的取值存在主要作用区间这一结论。

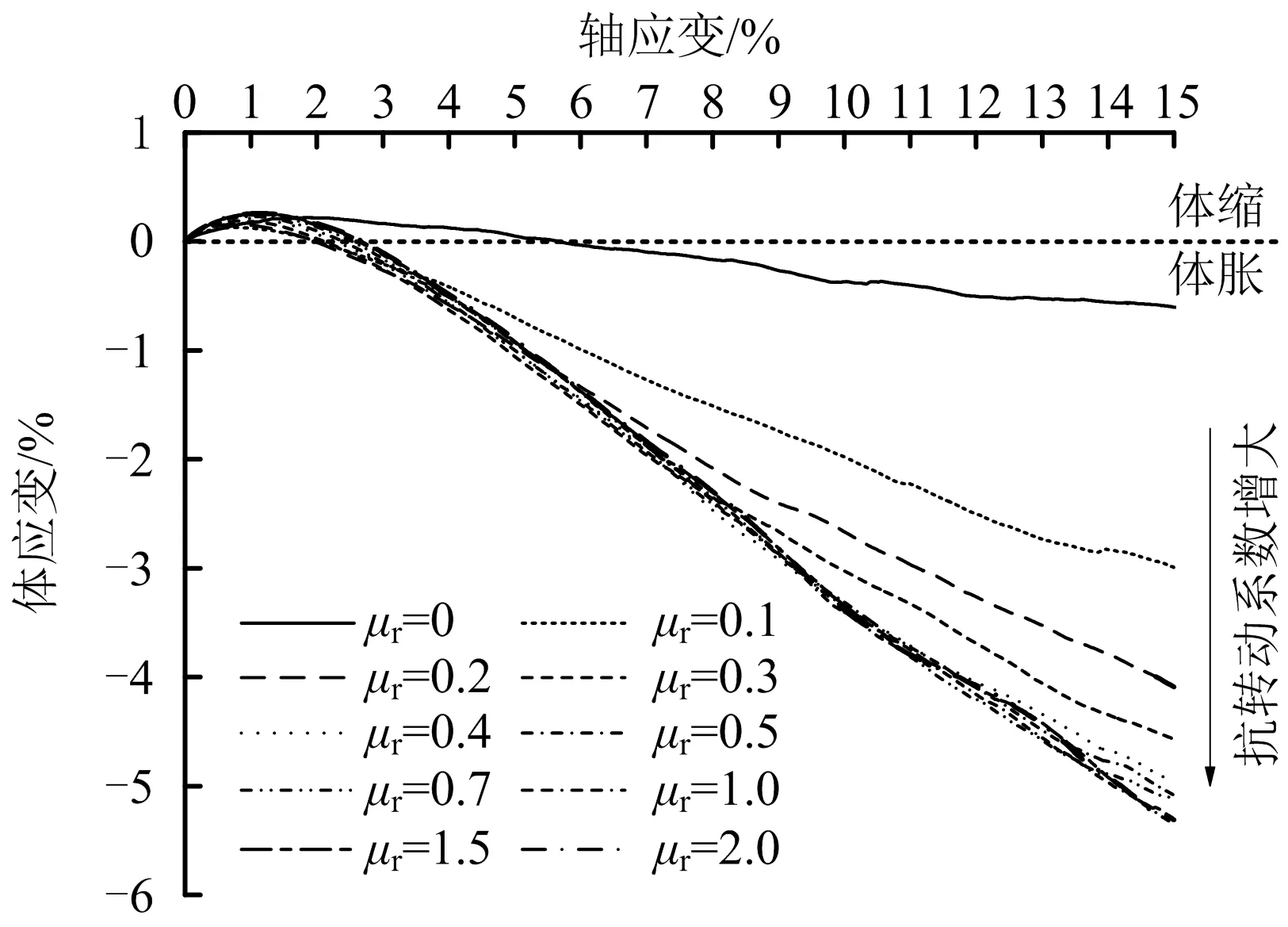
图12 100 kPa围压时不同抗转动系数下的体应变-轴应变曲线

3 基于随机森林回归模型的参数权重分析

由于模型的参数间存在一定的交互作用，即多个细观参数会对单个宏观参数共同产生影响。而以上控制变量试验无法精确体现出影响的权重，因此引入随机森林机器学习法作为工具，对参数进行进一步的精细化分析。

随机森林算法是广泛使用于计算机领域的1种机器学习算法，其基于决策树与bagging思想，通过建立多棵决策树以提高预测性能，其预测值由各棵树输出的平均数所决定[15]。该算法具有权重分析功能，可以考察各个自变量特征的重要性。

本文基于抗转动线性接触模型开展300组随机细观参数的三轴试验，并利用python语言sklearn库基于随机森林算法建立预测模型，根据文献[16]与本文模拟结果，确定主要参数范围，见表4。

表4 随机参数范围

3.1 模型建立过程

以模型的4个自有参数作为输入层参数，以初始弹性模量、泊松比与最大偏应力3个参数作为输出层参数，并随机选取300组数据中的240组作为训练集，60组作为测试集，以拟合度R2作为模型好坏评估的指标。

3.2 模型调参

随机森林模型具有较多的模型参数，正确的参数选择能够减少模型过拟合并保证其具有较高的准确度和泛化性能。其中回归树数量n_estmators与最大树深max_depth2个参数对模型优劣起着重要作用。采用网格搜索法找到最佳模型参数，所建立模型的优劣以拟合优度R2为考察指标，所得参数和模拟结果见表5，结果表明，训练的模型具有较高的准确性。

表5 随机森林模型参数与拟合度

3.3 权重分析

由于随机森林模型存在随机性，每次训练均可能得到规律相同但权重系数有一定差别的结果，因此为消除其影响，用相同的模型参数训练10 000次模型再对权重参数取平均值作为最终结果。

随机森林输出的宏细观参数权重柱状图如图13所示。由图13可知，权重值越大代表影响程度越大，其总体规律与本文对比试验结果相似。其中，抗转动系数(0.564 72)与摩擦系数(0.427 5)显著影响试样的最大偏应力且前者的影响偏大；刚度比主要对泊松比(0.751)产生决定性影响，对初始弹性模量(0.201 57)起次要作用；有效模量对初始弹性模量(0.695 14)起主要作用，而对泊松比(0.193 64)起次要作用。

图13 随机森林输出的宏细观参数权重柱状图

4 结论

1)试样的变形参数主要受颗粒有效模量与刚度比的影响。有效模量的增加会显著增加试样的初始弹性模量且增加试样的泊松比。刚度比的增加会显著降低试样的初始弹性模量且增加泊松比。

2)试样的强度参数主要受颗粒间摩擦系数与抗转动系数的影响。摩擦系数的增加会显著增加试样的峰值强度而几乎不影响试样的残余强度；而抗转动系数的取值存在作用区间，当抗转动系数处于区间内时，试样的峰值强度与残余强度会随着抗转动系数的增大而增大，而当抗转动系数取值大于区间时，试样的峰值强度与残余强度将不再增加。此外，抗转动系数与试样的剪胀性显著相关。

3)随机森林可以较好地表征宏细观参数中的影响关系。对于试样初始弹性模量而言，主要因素的影响权重排序为有效模量(0.695 14)>刚度比(0.201 57)；对于试样泊松比而言，主要因素的影响权重排序为刚度比(0.751)>有效模量(0.193 64)；对于试样峰值而言，主要因素的影响权重排序为抗转动系数(0.564 72)>摩擦系数(0.427 5)。