频繁矿震下临近建筑物结构疲劳损伤及安全选址研究*

王凯旋，胡 萍，周建新

(中国安全生产科学研究院，北京 100012)

0 引言

矿产资源在国民经济与社会发展中具有重要地位，但矿产资源开发过程中引起的周边环境扰动和建筑结构损伤时有发生，这不仅对矿山安全生产和矿工生命安全造成直接危害，还常有矿山地质灾害发生，对周边建筑物和居民的生命财产安全构成威胁。

近年来矿山爆破振动下建筑物的力学响应问题成为学术界的热点和难点问题，相关研究成果较多。范勇等[1]运用基于确定的高端墙爆破振动安全控制标准，对侧向爆破荷载作用下地下厂房高端墙安全性进行分析；贾磊等[2]建立爆破施工对既有衬砌振动影响的数值模型，给出数值计算中爆破荷载的波形、荷载峰值、加载时间的模拟方法，并研究爆破开挖进尺、间距及埋深等因素对既有邻近隧道的影响；包辉[3]基于大量爆破振动实际监测效据，对爆破振动速度反应谱谱面积SR与爆破地震波信号各特征量进行关联分析，研究SR对建筑结构振动损伤的影响和关联；李永靖[4]运用疲劳累计损伤理论，建立频繁矿震作用下钢筋混凝土框架结构层次上的损伤模型；吴仕鹏[5]系统归纳爆破振动波的形成、参数及影响，对振动荷载作用下建筑物发生共振的现象进行理论分析，形成单、多自由度体系的振动方程；张玉成等[6]针对隧道开挖爆破施工对既有建筑物的影响，将孔状爆破荷载等效成面荷载进行爆炸作用的模拟，使得数值分析更加简化；董陇军等[7]对质点振动速度、爆破振动主频率等8个影响因子进行分析研究，建立露天采矿爆破振动对砌体结构破坏效应预测的Fisher判别模型。

鉴于此，研究矿山爆破振动对于周边环境及人员保护具有重要意义。目前学者们针对矿山开采诱发的矿震影响研究主要包括以下2种思路：1)对建筑物简化为仅考虑烈度因素，从而分析单次地震荷载作用下的结构力学响应；2)仅针对单个结构构件，依据实验中试块在频繁振动荷载作用的累积损伤规律，得到经验性的结构累积损伤模型。现有研究主要包括以下需要改进的内容：1)需准确描述振动波如何通过岩土体传递至建筑物，并给出爆破振动源与建筑物在不同间距下结构的加速度反应谱或位移反应谱；2)需加强对频繁矿震下的结构累积损伤破坏规律的监测，辅以理论经验公式和数值模拟成果进行验证和拓展分析；3)需针对不同的建筑物正常使用要求，给出频繁矿震相应的爆破安全允许距离。

综上所述，本文根据某铁矿实际作业区内拟规划建筑物的工程案例，对结构累积损伤和拟规划建筑选址进行研究；现场开展振动监测并结合修正后的撒道夫斯基公式得到振动速度等参数，依据不同类型建筑物正常使用相应的振动速度，得到单次爆破振动安全允许距离；采用ANSYS有限元建模得到频繁爆破振动下建筑物的动力力学响应，并分析结构软化效应和应力疲劳损伤，从而指导投资及规划建设。

1 爆破振动下建筑物结构损伤机理

1.1 爆破振动引发建筑物共振

爆破振动破坏效应实质上是1个动态破坏过程，爆破瞬间产生巨大的能量并以能量波的形式沿介质向四周扩散，引起质点振动。楼房可简化成下端为固定支座、上端为自由支座的构件杆。爆破产生的动力荷载-应力波传递形式有径向、切向和垂向3种形式，分别引起建筑物“水平摇摆” “左右扭转”和“上下颠簸”，如同在风荷载的作用下，建筑物产生“鞭梢效应”，此时建筑物顶端振动及变形最大[8]。由于建筑物结构型式和构件连接变化多样，在复杂应力共同作用下，某些门窗洞口、楼梯间等位置可能产生应力集中破坏或微损伤，故不能简化为均质的弹性体。

1.2 环境扰动引起结构二次损伤

在复杂的地质环境下，爆破产生的动力荷载-应力波在岩层节理或断层带发生发射和折射，对周边岩层承载结构产生扰动，应力应变状态变化，形成断裂带，甚至发生土层的“喷砂” “液化”的现象，或引起采空区塌陷，进而诱发矿震，对建筑物结构产生二次伤害。

1.3 爆破振动下结构损伤的影响因素

根据文献[9]及试验测试分析，得出爆破振动下建筑物结构损伤的影响因素来源主要为地质条件、爆破源及建筑物3个方面，见表1。

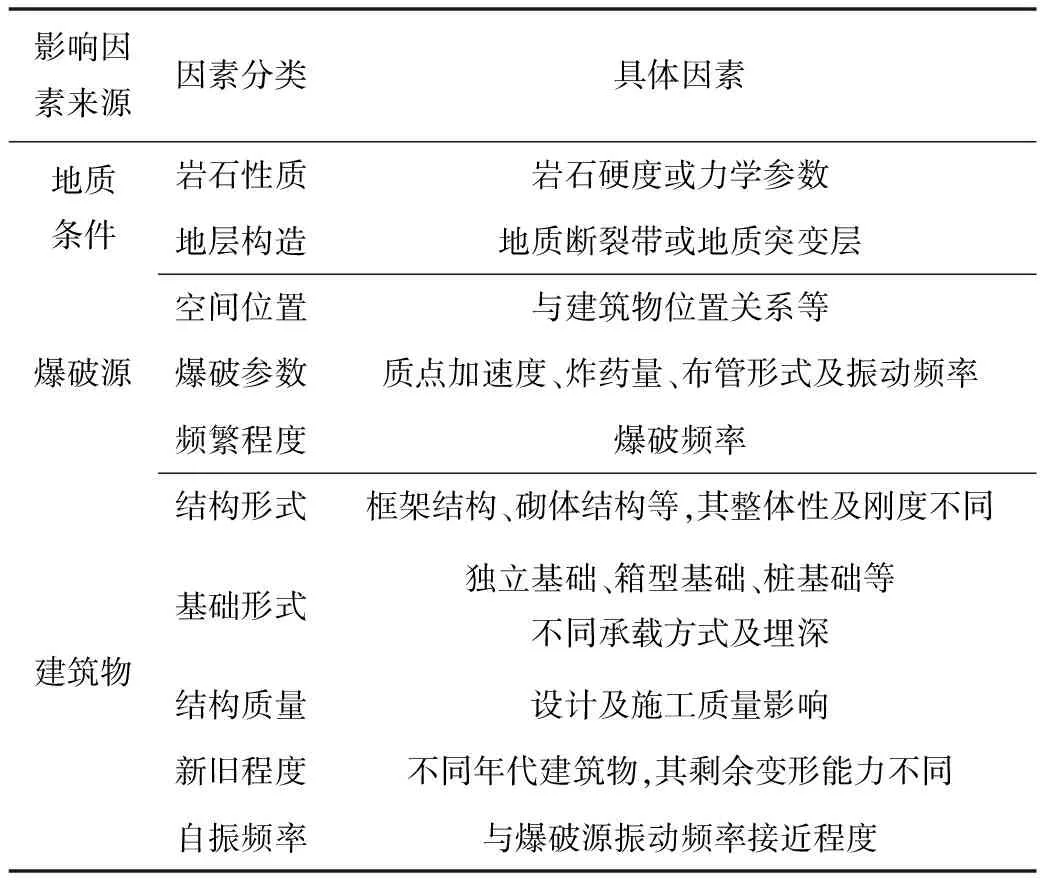
表1 影响因素分类及内容

2 矿爆临近建筑物安全允许距离

北京某铁矿厂建于1971年，采用无底柱分段崩落法，利用凿岩台车钻凿1～2排76～80 mm的扇形炮孔，装填黏性粒状铵油炸药，最大起爆药量1 780～1 920 kg/次，单响最大药量为72 kg。矿爆作业区内规划建设科研基地项目，总面积约2万m2。

2.1 震动参数确定

采用NUBOX-6016型智能振动监测仪，使用石膏作为传感器与地表岩石之间的黏结剂，确保传感器与地表岩石粘合固结良好，如图1所示。在拟规划建设区域内，测点距离爆破源位置150 m左右。测得爆破振动时间-加速度曲线，如图2所示。

图1 爆破振动传感器安装

图2 爆破振动波的时间-加速度曲线

2.2 单次振动时建筑物安全允许距离

《爆破安全规程》(GB 6722—2014)[10]中对建筑物保护的爆破振动速度安全允许标准进行划分，见表2。

表2 爆破振动速度安全允许标准

铁矿作业区地形复杂，且受高差、采空区等多重因素影响，为便于计算分析，假定不考虑地质及建筑物因素的作用，仅考虑爆破振动源的影响，则振动速度的撒道夫斯基公式[10]修正为式(1)：

(1)

式中：V为振动速度，mm/s；Q为炸药量，kg；R为爆心距，m；K，α为与爆破点地形、地质等条件有关的系数和衰减指数，根据《爆破安全规程》，取α=1.3，K=300(软岩石)；n为与装药条件和爆心距有关的指数，爆心距较大时取为1/3；δ为高差影响系数，根据测试数据确定，取1。根据式(1)，假定药量Q和爆心位置不变，得出爆破振动安全允许距离r，如式(2)所示：

(2)

取可以确保不同形式和用途的建筑物正常使用的振动速度V进行计算，得到相应的爆破振动安全允许距离r，如图3所示。

由式(2)与图3可知，爆破振动安全允许距离r与振动速度V呈负相关，建筑物抵抗振动能力越强，允许振动速度越大，则相应爆破振动安全允许距离r越小，故建筑物抵抗振动能力的排序为：钢混结构房屋>砌体结构房屋>新浇混凝土养护>建筑物内有精密科研设备使用。对于图3所示的4种建筑物，图3(a)～(c)均在r之外，可以正常使用，而图3(d)在r之内，矿爆会对精密科研设备的正常使用造成一定影响。考虑到频繁爆破振动对建筑物正常使用的影响，建议拟规划建设的项目应重新选址且距离爆破振动源位置200 m以上(一般居住或办公用途)或1 km以上(精密仪器设备等用途)。

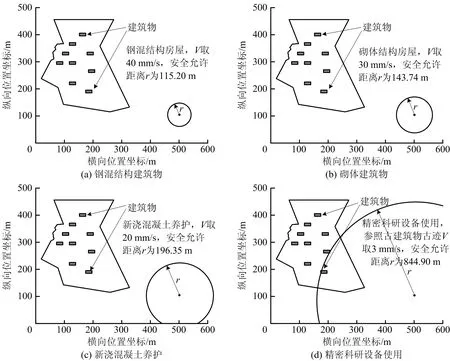
图3 对应不同建筑形式和用途的爆破振动安全允许距离

3 长期频繁振动作用下建筑物结构安全寿命预测

单次爆破振动对建筑物安全使用不会构成威胁，仅会对部分精密仪器的使用造成不利影响，但矿震长期作用下的结构累积损伤不可忽视[11]。建筑物结构累计损伤可以通过结构强度、刚度的退化或应变、固有频率的变化来表征，这里采用结构固有频率变化来求解建筑物第j个构件的损伤值dj，如式(3)所示[12]：

(3)

式中：f0为构件初始时的固有频率，Hz；fj为构件损伤后的固有频率，Hz。

根据建筑物各个构件的频率变化和线性加权组合方法得到整体结构的损伤值D，如式(4)所示：

(4)

式中：f0j为第j个构件初始时的固有频率，Hz；fij为第j个构件损伤后的固有频率，Hz。

由此可见，通过现场测试得到结构固有频率变化，求得整体损伤值D及达到容许损伤值时的振动次数N，如式(5)所示[13]：

N=12·f·t·n·y

(5)

式中：N为建筑物受疲劳次数；f为平均振动频率，Hz；t为平均波延时间，s；n为平均每月爆破次数，次/月；y建筑物服役年限，a。

建筑物、桥梁、海上平台和大多数金属结构构件的疲劳失效应力循环次数N一般为104～107次，在强震作用下，建筑物在疲劳失效前应力循环次数N一般会小于104。根据经验测算铁矿爆破平均振动频率为9.03 Hz，平均波延时间为1.0 s，平均每月爆破次数为60次，考虑铁矿爆破点最不利(最近)位置，取N为105，根据式(5)求得y约为15 a。

4 建筑物结构累计疲劳损伤数值分析

设定某三层框架结构建筑建设在该矿区爆破振动影响区域内，利用ANSYS有限元软件进行建模分析，模型如图4所示。建筑物高3.6 m，中跨2.1 m，边跨7.5 m，柱截面尺寸550 mm×550 mm，承重结构采用C30混凝土，初始弹性模量为3.14×104N/mm2，初始泊松比为0.2。

图4 建筑物模型

ANSYS建模分析中，关键参数和设置如下：1)结构均采用实体单元solid186；2)材料为均质线弹性，弹性模量随振动次数增加而逐步衰减；3)钢筋和混凝土为bond接触，结构之间为绑定接触；4)楼体底部固定，约束所有方向的位移和转动；5)振动载荷根据图2中时间-加速度曲线施加于楼体。

考虑到在频繁的爆破振动荷载作用下，建筑物结构弹性模量、泊松比会发生变化，因此在每次输入爆破振动波前，根据经验公式(6)～(9)计算N次爆破振动波作用后[14-17]的弹性模量E、泊松比ν。分别取N=5 000，10 000，15 000，20 000次时，对应的弹性模量E、泊松比ν与矿震次数的关系如图5所示。

图5 矿震次数与弹性模量、泊松比的关系

(6)

(7)

lgNf=-0.853 1E02+4.461 7E0-1.266 2

(8)

lgSmax=-0.002 3-0.027 5lgNf

(9)

式中：Smax为应力系数；Nf为疲劳极限次数；E0为初始弹性模量，GPa；ν0为初始泊松比。

经数值计算分析，爆破振动次数N分别为5 000，10 000，15 000，20 000时，建筑物各部位结构位移和应力结果如图6～9所示。矿震次数与结构力学响应的关系如图10所示。

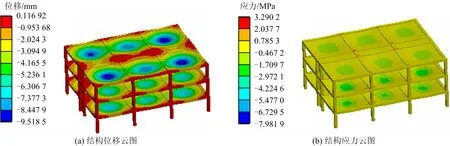
图6 矿震5 000次时结构力学响应云图

图7 矿震10 000次时结构力学响应云图

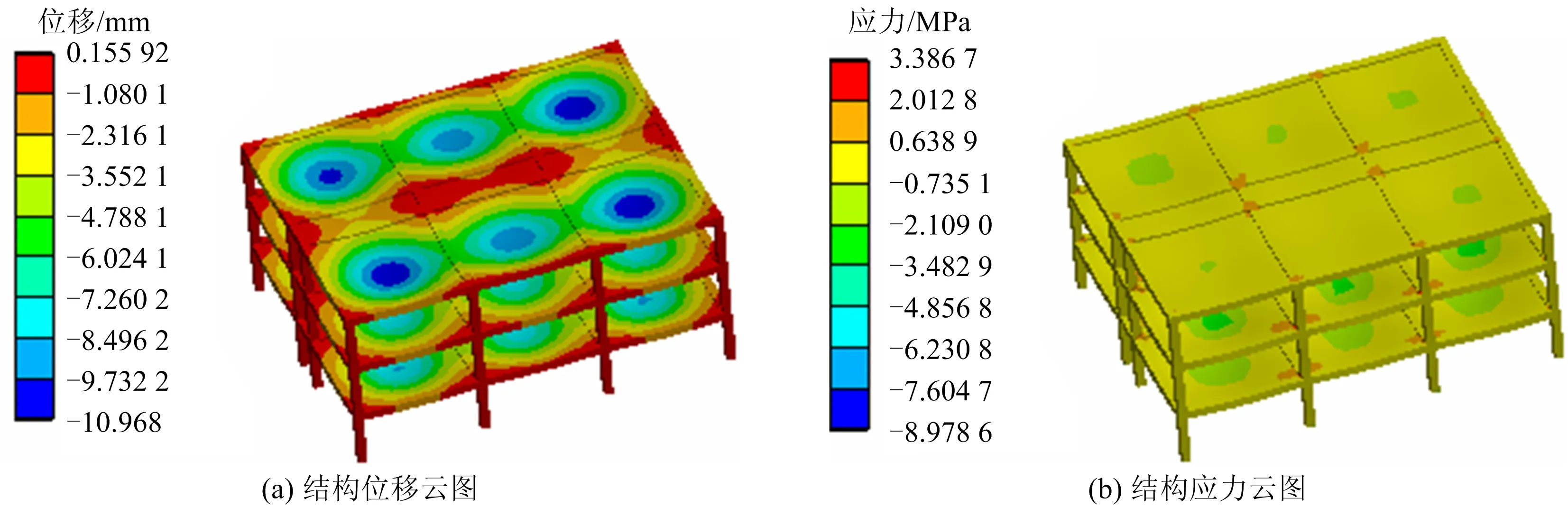
图8 矿震15 000次时结构力学响应云图

图9 矿震20 000次时结构力学响应云图

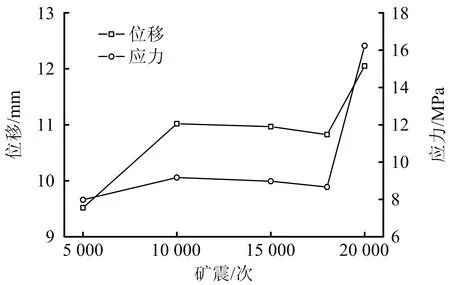
图10 矿震次数与结构力学响应的关系

结合图5～10可知，结构的弹性模量随着矿震次数的增加而减小，泊松比随着振动次数的增加呈现先减小后增大的规律，说明爆破振动会使结构出现“软化”趋势，应力与位移先增大、后缓慢减小，后迅速增大。发生此种现象的原因可能是过程中多次振动导致钢筋混凝土内部结构改变，从而释放一部分应力，当振动次数继续增加时楼体会发生二次破坏，使得弹性模量又迅速减小，应力也会极速增加。当振动超过15 000次后钢筋混凝土内部组织结构更加紧密，位移变小，但压应力迅速增加，当振动次数超过20 000次时(每天振动2次，约27 a)，建筑物压应力已超过破坏极限应力。

5 结论

1)建筑物抵抗振动能力越强，允许振动速度越大，相应爆破振动安全允许距离越小。建议拟规划建设的项目选址需距离爆破振动源位置200 m以上(一般居住或办公用途)或1 km以上(精密仪器设备等用途)。

2)爆破微振动会使结构出现“软化”趋势，当振动次数超过20 000次时(每天振动2次，约27 a)，结构压应力已超过破坏极限应力。

3)设定矿山开采界限，根据建筑物实施阶段的敏感性调整爆破参数，并采用改良型炸药或改进开发方法。建设项目规划设计阶段采用先进抗震隔震技术，做好结构及基础选型，保证施工质量。

4)做好岩土勘察工作，重点排查建设用地范围内有无地质断层或地下空洞存在，防止次生灾害的发生。利用信息化及人工智能技术手段，做好建筑物及周边地形地貌的实时动态监测和险情预警，并对建筑物关键部位进行结构安全评估。