半正态分布参数的序贯概率比检验
2021-07-09胡宏昌
胡宏昌, 王 婧
(湖北师范大学 数学与统计学院,湖北 黄石435002)
1 引 言
序贯分析法是A.Wald在二战期间为满足军火的质检工作而提出的,序贯概率比检验是序贯分析的重要内容之一,其成果丰富(参见文献[1-4]).文献[1]对序贯概率比检验作了较系统地介绍,给出了在伯努利分布和正态分布的序贯概率比检验,并且利用随机游动的性质导出序贯概率比检验(SPRT)的统计性质;文献[5-6]分别研究了指数分布和泊松分布中参数的序贯概率比检验,给出了相应情形下序贯概率比检验平均样本容量计算公式,并进行了随机模拟.
正态分布是最重要而又非常常见的分布,由该分布可以产生半正态分布.关于半正态分布的研究成果虽然不能与正态分布相提并论,但还是存在一些(参见文献[7-10]),其中文献[9-10]给出了半正态分布的相关结论.然而,似乎没有人研究半正态分布的序贯概率比检验,本文将对此进行初步探讨,以便拓宽大学生在学习《概率论》和《数理统计学》的相关知识和视野.
2 半正态分布中参数的序贯概率比检验
先给出半正态分布的定义,然后用SPRT法研究半正态分布中参数的检验问题.
定义[7]如果随机变量X的概率密度为
其中参数θ>0,则称随机变量X服从参数为θ的半正态分布,简记为X~HN(θ).
设X1,X2,…取自总体X~HN(θ)的一个样本,其观测值为x1,x2,….讨论如下简单的假设检验问题:
H1∶θ=θ1↔H2∶θ=θ2(其中不妨设0<θ1<θ2).
为此,考虑似然比统计量
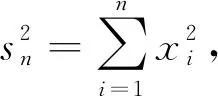
(1)
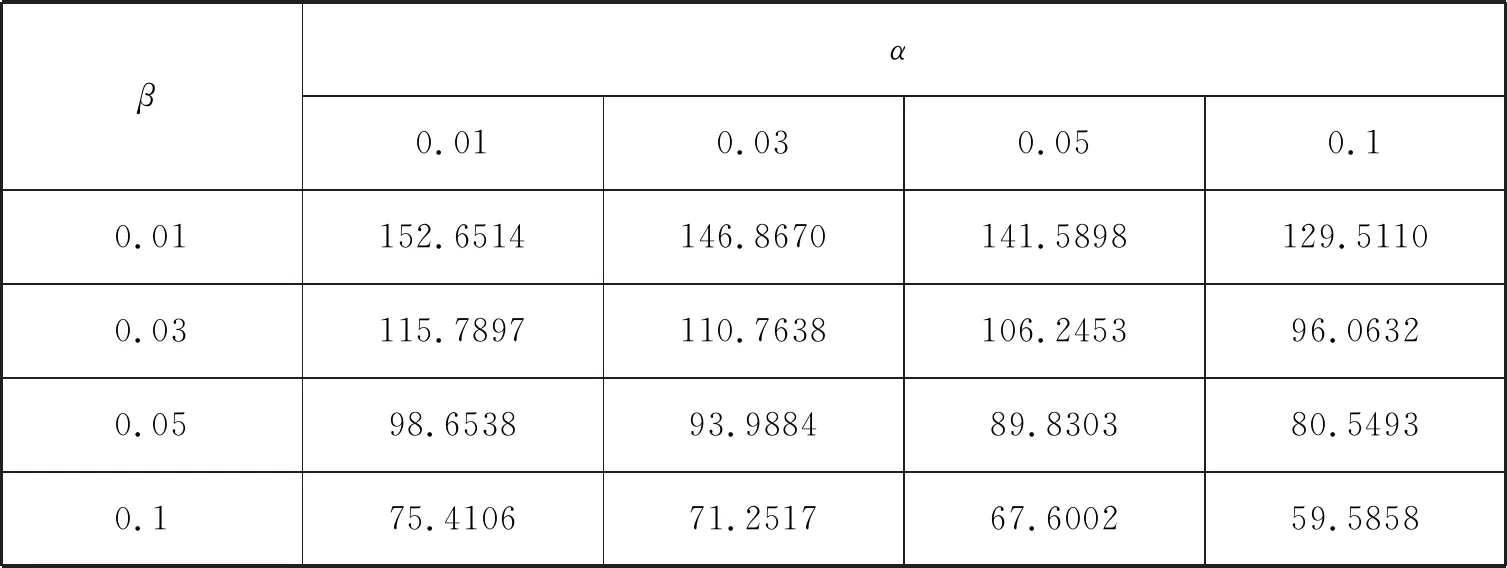
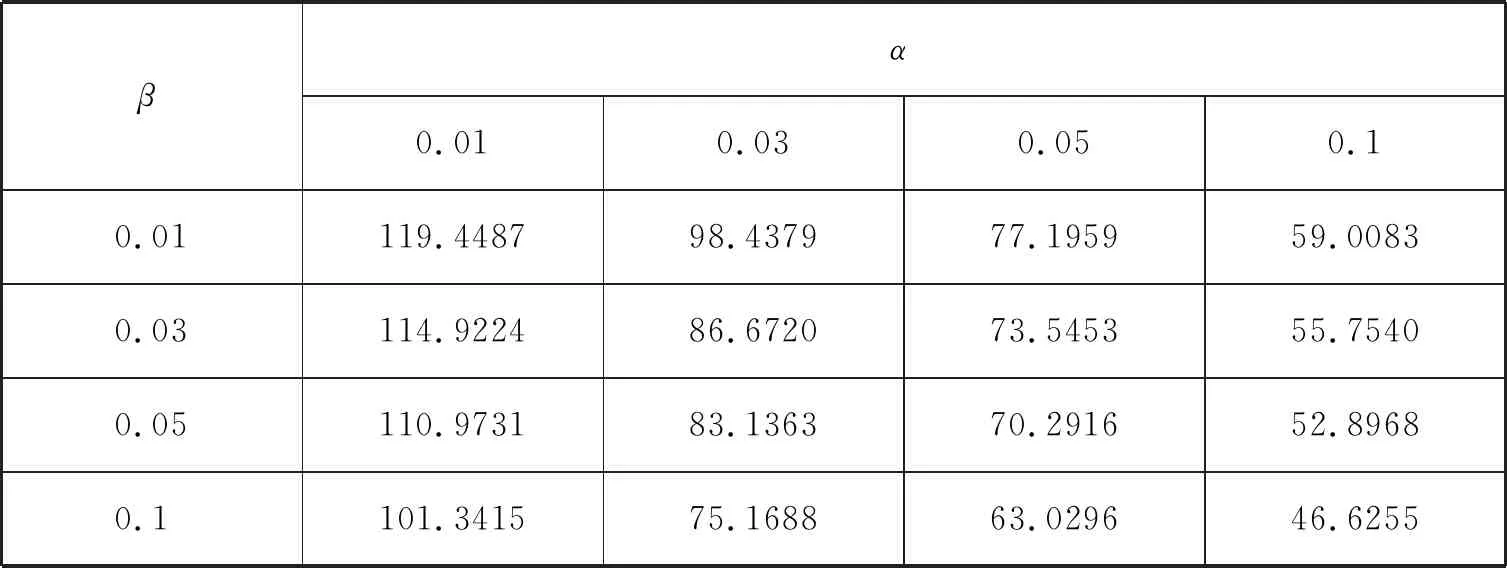
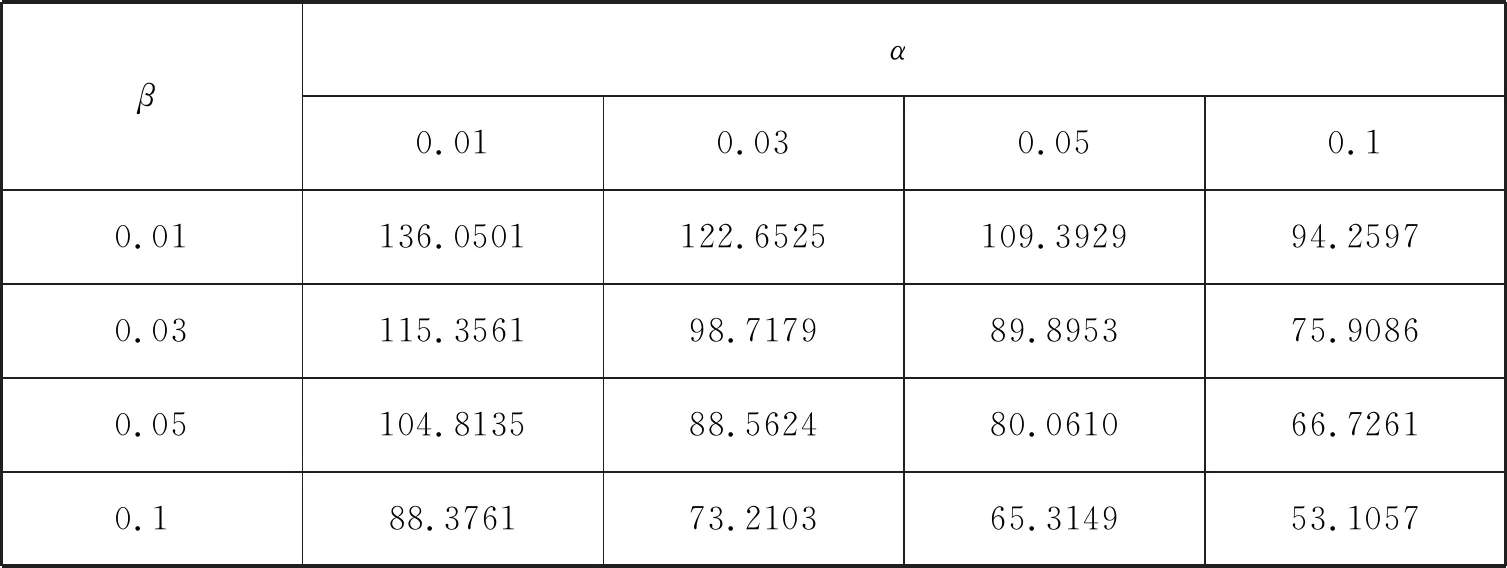
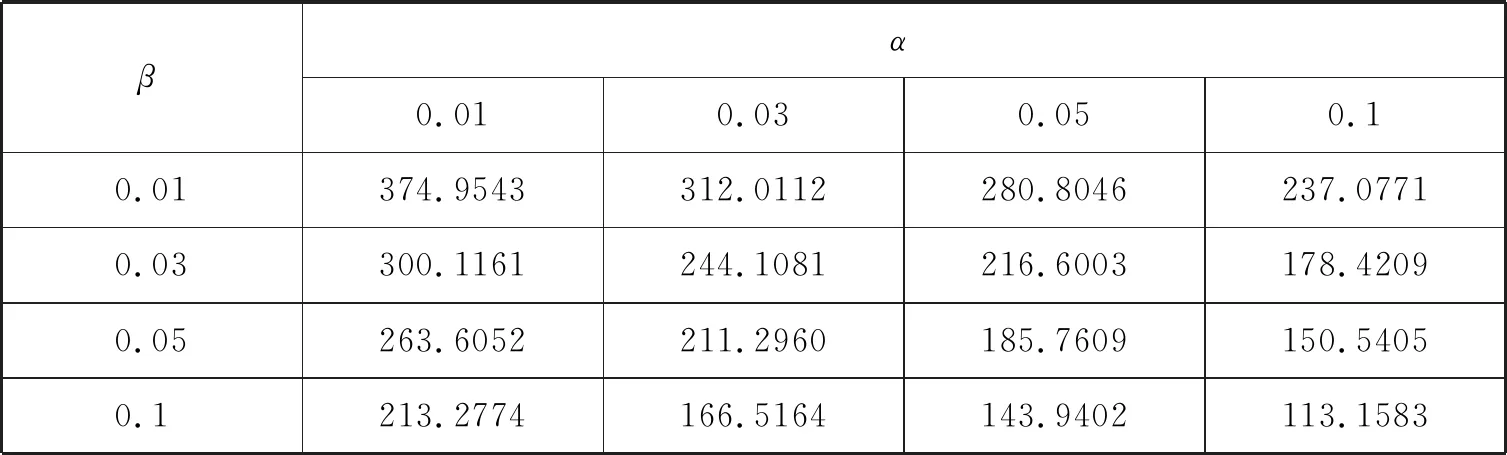
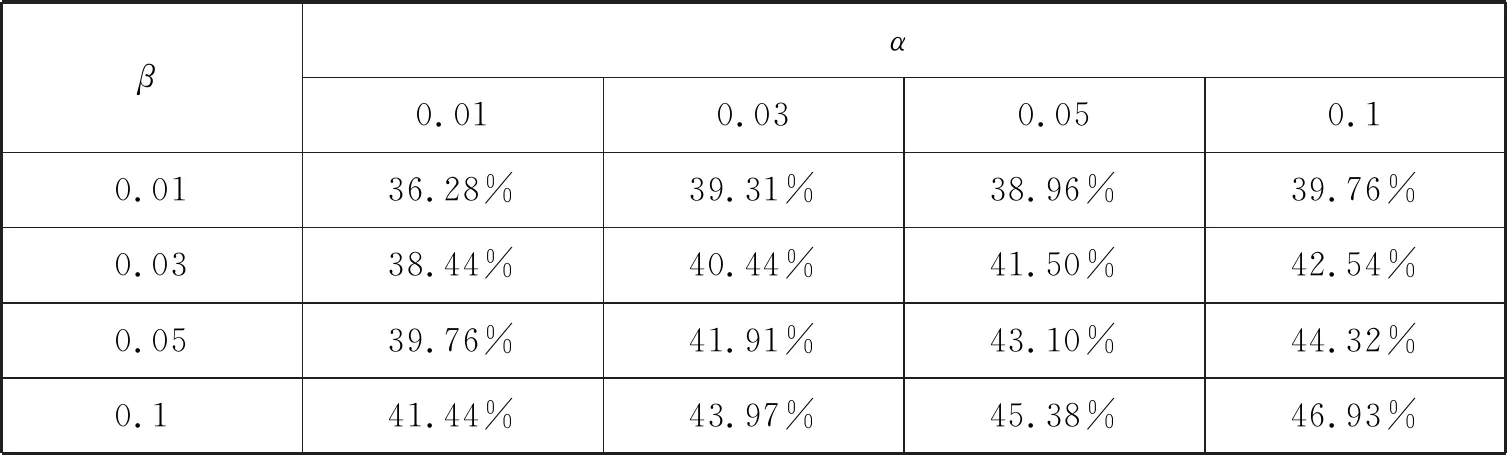
对于给定的两个常数A,B(0 则当λn≥B时,可得 (2) 当λn≤A时,可得 (3) 于是由(2),(3)式可得停止法则为 (4) 性质1令Zi=ln(f(Xi,θ2)/f(Xi,θ1)),则存在函数h=h(θ)≠0使得E(exp{hZ1})=1. 由介值性定理容易证明下式成立 由此即可得到E(exp{hZ1})=1. 性质2[1]若存在h=h(θ)≠0使得E(exp{hZ1})=1,则检验的操作特性函数的近似公式为 性质3平均样本容量的近似计算公式如下: 证由于EX2=θ2, EX4=3θ4(参见文献[7]),所以 (5) (6) (7) 这里Eθ1τ*, Eθ2τ*由下面四种情形确定: (8) (9) 其中 (10) (11) 其中 下面举出一例将SPRT法与Neyman-Pearson检验法所需平均样本容量进行比较,说明前者优于后者. 取θ1=1.0,θ2=1.2,在给定的检验水平下SPRT法所需要的平均样本容量的近似值见表1、表2及表3. 表1 Eθ1τ*的近似值 表2 Eθ2τ*的近似值 表3 Eτ*的近似值 为了说明SPRT法的优越性,将其平均样本容量(见表3)与使用Neyman-Pearson检验法时所需要的平均样本容量n(见下表4)相比较(见表5).为此,先给出n的表达式. 表4 N-P检验法下的最优样本容量 表5 SPRT平均样本量与N-P检验法的最优样本容量之比 由中心极限定理得 从而经计算可得 其中uα,u1-β为标准正态分布的分位数. 由表5可知,在半正态分布中,SPRT所得平均样本量相对于N-P检验法最优样本量的占比最少约为36.28%,最多约为46.93%,占比均在35%-50%之间.序贯概率比检验中所得的平均样本容量要比固定样本容量的最优检验所得的样本量还要少得多,由此可显现序贯概率比检验高效的特点. 本文考虑了半正态分布中参数的序贯概率比检验,主要得到了检验的停止法则、操作特性函数和平均样本容量,并用模拟算例说明了序贯概率比检验中所得的平均样本容量要比固定样本容量的最优检验所得的样本量还要少得多.这些内容将在正态分布和假设检验的教学中具有指导作用,拓宽高校大学生的统计学知识和视野. 致谢本文在参考了陈家鼎教授等十篇文献的基础上完成,采纳了审稿专家的宝贵修改意见.为此,对相关作者及审稿人表示衷心的感谢!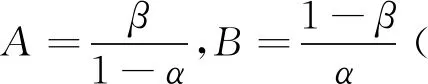
3 SPRT的一些性质
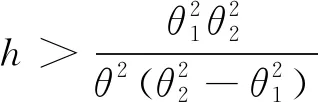
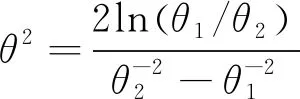
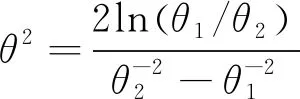


4 模拟算例
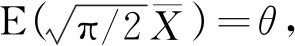
5 结 论
