多元积分的降维计算法

罗志刚

(湖北工业大学 理学院， 武汉430068)

1 引 言

下文提到的函数及其导数或偏导数都满足问题所需要的连续性，所说的“多元积分”包括平面区域上的二重积分、空间区域上的三重积分、第二类曲面积分以及这些概念向更高维空间中的推广.

凑微分法、换元法和分部积分法是计算一元函数积分的重要手段.但是，对于多元函数的积分，这些方法却难以在重积分号下直接应用，除非事先用Fubini定理将多元积分化成累次积分，然后去计算一元函数的积分.以平面区域D上的二重积分

(1)

为例，如果将二重微分号“dxdy”理解成微分元dx与dy的普通乘积，那么在作变量替换x=x(u，v)，y=y(u，v)后，换元公式

2 解决方案

2.1 普通积分和外积分

解决上述问题的关键是将二重微分符号“dxdy”解释成满足反交换性的外积(实质上就是对积分区域规定了方向)

dx∧dy=-dy∧dx，

并且去考虑积分

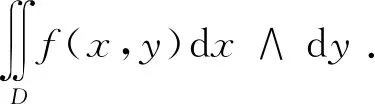
(2)

这种积分的被积式其实是一个外微分形式.外微分形式是可以作形式运算的对象：它可以自由进行变量替换，也能进行凑微分(凑微分实际上是第一类变量替换)和分部积分.因此，讨论多元积分的凑微分和分部积分问题的正确出发点不是(1)式而是(2)式.为了相区别，本文将(1)称为普通积分，(2)称为外积分(注意，“外积分”不是一个已经被大家采用的标准术语，仅仅在本文中使用).通常的微积分课程中定义的二重积分和三重积分就是普通积分.

尽管如此，普通积分与外积分之间还是有联系的.如果对积分区域取合适的定向(右手定向)，就可以使得外积分正好与普通积分相等

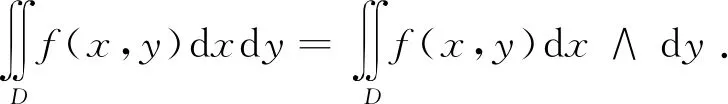
(3)

计算普通积分时，为了能用上外积分和外微分形式带给我们的便利，要先作这一步转换，即将普通积分与一个外积分相关联起来，然后去计算这个外积分.

2.2 外微分形式及其运算

高维空间中的外微分形式的一般理论可以参考文献[1-3].为了避免过于抽象和形式化，这里只以二维空间和三维空间的情形为例子来说明其计算规则.

二维空间的外微分形式有三种：

ω0=φ(x，y)，
ω1=P(x，y)dx+Q(x，y)dy，
ω2=f(x，y)dx∧dy.

(4)

它们分别称为0-形式，1-形式和2-形式.0-形式就是普通函数，1-形式是dx和dy的线性式，2-形式是dx∧dy的线性式.三维空间的外微分形式有四种：

(5)

由于∧运算满足反交换性，两个相同的微分元间作外积运算(比如dx∧dx)将得到零，所以二维空间的外微分形式不高于二次，三维空间的外微分形式不高于三次.

同一空间上的两个外微分形式之间可以作外积，也可以对外微分形式再作微分(外微分).一般地，可以证明(当然，对上述二维空间和三维空间中的外微分形式可以通过直接计算来验证)：

引理1[1](i)对任意两个外微分形式的外积求微分的规则：

d(ω1∧ω2)=dω1∧ω2+(-1)pω1∧dω2，

(6)

其中ω1是p-形式；

(ii) (Poincare引理) 对任意外微分形式连续作两次微分的结果为零：

d2ω=0.

(7)

对外微分形式作变量替换是直截了当的.例如，假定要对(4)中的ω2作第一类换元

ξ=φ1(x，y)，η=φ2(x，y).

根据外微分和外积的计算规则，有

(8)

括号内其实就是Jacobi行列式.所以

(9)

如果将式(8)写成

(10)

则换元后的结果(9)可以用如下的形式化计算直接得到

这正是一元函数中的“微分形式不变性”向多元函数的推广.这种推广也意味着在计算多元积分时，如果将被积分式看作外微分形式，换元法和凑微分法将可以直接在积分号下应用.

2.3 对外微分形式的积分(外积分)

如2.1小节所述，外微分形式还可以作积分.普通微积分课中讨论的第二类曲线积分和第二类曲面积分便是不同次数的外微分形式在流形(如曲线和曲面)上积分的具体例子.关于这些积分，有一个十分重要的定理：

引理2(广义Stokes公式) 在任何流形S及其边界∂S上，对于外微分形式ω，有

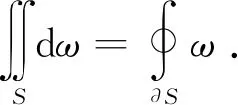
(11)

这个定理的一般情形证明较复杂，读者可以参考专著[3]，但它在二维空间以及三维空间的特例就是大家熟知的Green公式、Stoke公式和Gauss公式.广义Stokes公式的作用如同Newton-Leibniz公式一样：它们都将流形上的积分与流形边界上的积分联系了起来[2].

2.4 计算多元积分的降维法

算出积分的关键在于“降维”，Newton-Leibniz公式如此，化累次积分的方法也如此.广义Stokes公式(11)左边的被积式是比右边高一次的外微分式，因此该公式也实现了“降维”，原则上它也可以作为计算多元积分的基础.然而，通常情况下，(11)左边为诸如(2)的形式，很难立刻找出ω使得dω=f(x，y)dx∧dy，这导致利用(11)实现“降维”比较困难.所以，在普通微积分课程中，几乎总是只从右边向左边用(11)式而不是反过来用，毕竟求一个已知外微分形式的外微分很容易.

有了外微分的计算规则以及前面讨论过的积分号下凑微分和变量替换的技巧，就可以使用这些规则和技巧一步步去找到符合要求的ω.下面写出这个计算方案中的关键定理.

如果被积式能化成dω1∧dω2，其中ω1，ω2是两个外微分形式，则有

定理1降维公式

(12)

证由(6)和(7)有

d(ω1∧dω2)=dω1∧dω2+(-1)pω1∧d2ω2=dω1∧dω2，

然后两边积分，应用一次广义Stokes公式(11)即证.

很多时候，被积式可能难以立即凑成dω1∧dω2这种形式，这种情况下可以用分部积分法：

定理2分部积分公式

(13)

证将(6)式两边积分，然后应用广义Stokes公式(11)即得.

上述定理1和定理2给出的公式并不见于其他文献或书籍，其名字是本文作者所取，是否合适还有待商榷.作为定理2的特例，对积分(2)，有

推论

(14)

证在(13)中取ω1=x，ω2=f(x，y)dy，然后注意到

以及ω1=x是0-形式，即证第一式.第二式

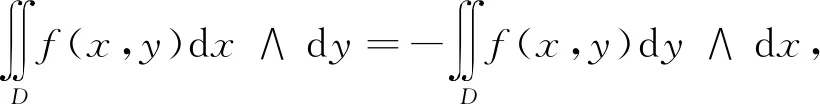
然后使用第一式已证明的结论，即得.类似的结论也能应用到三重积分.

文献[4-5]也研究过重积分的分部积分问题，得到的结果与这里的推论相当.由于没有采用外微分方法，他们的结果不容易记住，也难以推广到更高维的空间中去.

初等微积分课本一般不介绍外微分.即使介绍，也仅止于用来说明怎样将几个基本公式统一到广义的Stokes公式下[2]，很少注意到外微分运算实际上可以用来对被积式作凑微分以及分部积分等各种变换，更没有注意到广义Stokes公式(或降维公式)可以为多元积分的计算提供一种不同于化累次积分的新方案.这正是本文所特别要强调的内容.

3 计算示例

这一节举若干计算实例来具体说明上节中所阐述的方法.

第一个例子计算二维空间中的2-形式的外积分，所选择的问题的是求普通二重积分，因此第一步总是要将普通积分与适当定向了的平面区域上的外积分相关联起来，然后去计算相应的外积分.

解为了详细说明本文的方法，采用多种方法来计算.首先有

其中积分区域取正侧(即正z轴的那一侧)定向.之后，可以用前一节的方法来处理被积分式.

法1凑微分法. 按照外微分法则，可以得到

其中最后一步使用了降维公式(12)，将积分转化到边界∂D上.完成边界上的积分，有

注意，其中的σ和∂σ要正确定向.

法3分部积分法. 应用上一节中的推论(14)，得到

右边第二项

所以

下面的例子是计算三维空间中的2-形式在曲面上的积分.这种类型的积分实质上就是普通微积分课程中所讨论过的第二类曲面积分.

解考虑到曲面的定向，有

其中ω=(z2+x)dy∧dz-zdx∧dy，对ω的外积分在曲面S的上侧面作.

法1将积分分成两项，分别凑微分，然后转化到曲面边界上积分.第一项积分

上式右边第一项用降维公式(12)后算得

第二项使用公式(14)，得到

所以

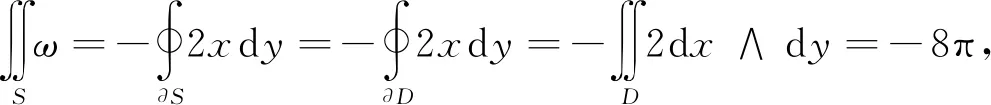
其中D={(x，y)|x2+y2≤4}.故原式=8π.

法2参数法(即换元法).用柱坐标系

x=ρcosθ，y=ρsinθ，z=ρ2/2，

参数所在的区域为σ={(ρ，θ)|0≤θ≤2π，0≤ρ≤2}，所以

从而

故原式=8π.其中考虑到问题的对称性，事先将明显为零的项省去了.当然，这个例子还有其他更简单的方法，此处不讨论.

关于怎样将一般形式的第二类曲面积分转换到对边界的积分，文献[6-7]给出了若干定理.例如，文献[6]中的定理3中的结论，用本文的方法可以这样得到

之后将最后一个积分中的被积式当作W(x，y，z)，反过来求积分可以得出P(x，y，z)，从而实现了“降维”，与文献[6]殊途同归.但本文的方法更简洁、更普遍、更易于应用.

最后，计算三维空间中的3-形式在区域V(已定向)上的外积分

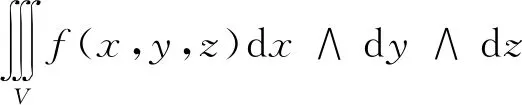
时，可以先利用降维方法转化成区域边界∂V上的第二类曲面积分，将∂V分片参数化之后按例2的方法作出其上的积分.我们选取文献[5]中的例子，用本文的方法来演示一遍.

解首先

这里V的定向是使得∂V的定向沿着外法向.

作柱坐标变换得dx∧dy∧dz=d(ρcosθ)∧d(ρsinθ)∧dz=ρdρ∧dθ∧dz，所以

其中，参数区域

σ={(ρ，θ，z)|0≤ρ≤1，0≤θ≤2π，0≤z≤ρ+1}.

又ρdρ∧dθ∧dz=ρdρ∧dθ∧d(z+ρ+1)=d(z+ρ+1)∧ρdρ∧dθ，分部积分后得到

第一项

第二项求出被积式中的外微分，之后作分部积分(或凑微分后直接使用降维公式(12))得

其中的参数区域

δ={(ρ，θ)|0≤ρ≤1，0≤θ≤2π}.

最后，将结果收集起来，有

这个例子综合使用了变量替换、凑微分、分部积分、降维等方法.值得注意的是，有了外微分的计算方法，这些技巧都可以在积分号下直接完成，无需记住太多的定理和公式.

此方案对于更高维空间中的各种外微分形式的积分仍然成立，在此无需举更多的例子.

4 结 论

只有考虑外微分形式的积分，多元积分的被积式才能自由地进行换元、凑微分和分部积分.结合广义Stokes公式，问题可以不断“降维”，从而得到一种无需化累次积分计算出多元积分的方法，其精神与使用Newton-Leibniz公式计算一元函数的积分相一致.文中列举了一些例子，说明这些方法都切实可行.

致谢感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.