有关直角双曲线的一些性质

王 庆， 周建伟

(1.苏州市职业大学 数理部，江苏 苏州215104； 2.苏州大学 数学科学学院， 江苏 苏州215006)

1 引 言

近来，作者用射影几何的方法研究直角双曲线，在《直角双曲线内接三角形的垂心问题》一文中，证明了直角双曲线也可以由它的内接三角形的垂心生成[1].本文在此基础上，进一步给出一些直角双曲线的性质，说明它们可以用除了内接三角形的垂心生成外的其它方法生成.讨论的工具主要是射影几何，可参看文献[2-4]或其它高等几何书籍.

2 主要结果与证明

用射影几何方法研究即是把讨论的对象看作拓广平面上的问题. 双曲线上有两个无穷远点，这两点的切线是双曲线的渐近线.双曲线是直角双曲线的条件是过这两个无穷远点的直线互相垂直.下面讨论的问题有些来源于文献[3].

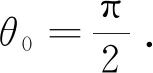
证如图1，设PA交AB的中垂线ξ于Q，φ1是线束A，B之间以ξ为轴的透视，φ1(AQ)=BQ； 设φ2是线束B以θ0为旋转角的旋转，φ2(BQ)=BP.φ1，φ2都是射影映射，由Steiner定理，线束A到B的射影映射φ=φ2∘φ1的对应直线的交点给出一条二次曲线，此曲线过A，B.不难证明ξ与AB的交点O是此二次曲线的对称中心.

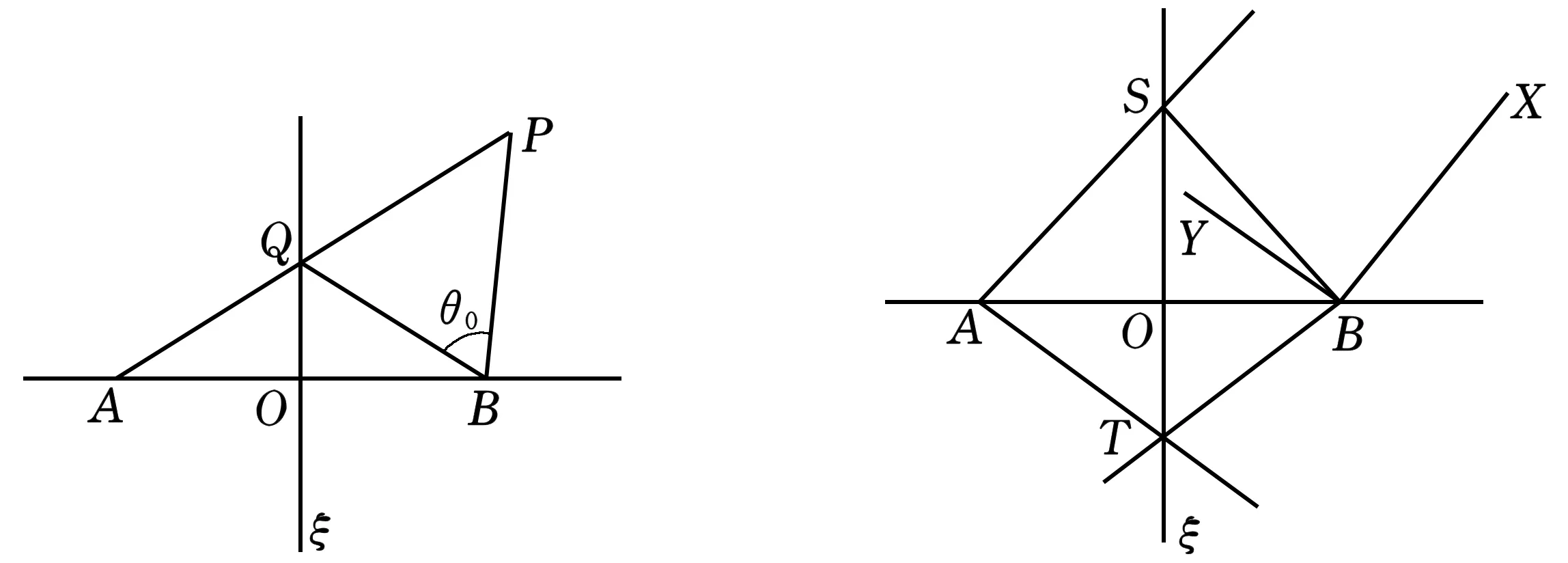
图1 图2

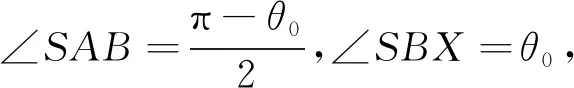
性质1给出的轨迹有两条分别对应于旋转角θ0与-θ0，它们关于直线ξ对称.

以AB为x轴，ξ为y轴，设A(-a，0)，B(a，0)，y轴上动点Q(0，t)，则BQ方向是 (-a，t)，BP的方向由BQ旋转-θ0得到，可算得BP的方向是(-acosθ0+tsinθ0，tcosθ0+asinθ0).直线AP，BP的方程分别是

消去t得直角双曲线：x2-y2-2xycotθ0=a2.

由此性质可得

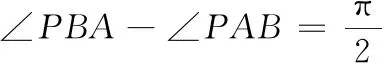
下面的两个性质可以用Steiner定理讨论，也可作为性质1的特例.

性质2设动直线平行于圆内接△ABC的边AC，分别交AB与C处切线于P，Q，则X=BQ×CP的轨迹是一条直角双曲线.

性质3设AB是圆的直径，P是圆上动点，Q在直线PB上使PA，QA与AB的夹角相等，则Q的轨迹是直角双曲线.

下面给出直角双曲线的另一种生成方法.

性质4在一族具有相同焦点的椭圆上，平行于定方向的切线上切点在直角双曲线上.

证设定方向不平行也不垂直于焦点的连线，否则轨迹退化为直线.设P∞是定方向给出的的无穷远点，如图3，对于一个以定点F1，F2为焦点的椭圆，设过点P的切线平行于给定方向，即此切线过P∞. 过焦点F2作此切线的垂线，垂足是X，与F1P交于X′，则F2X′=2F2X.设Q∞是直线F2X上无穷远点，P∞，Q∞都是定点，过它们的直线垂直.在定直线F2Q∞上，XX′给出一个射影映射，F2，Q∞是此映射的两个不动点.因此有下列射影映射，

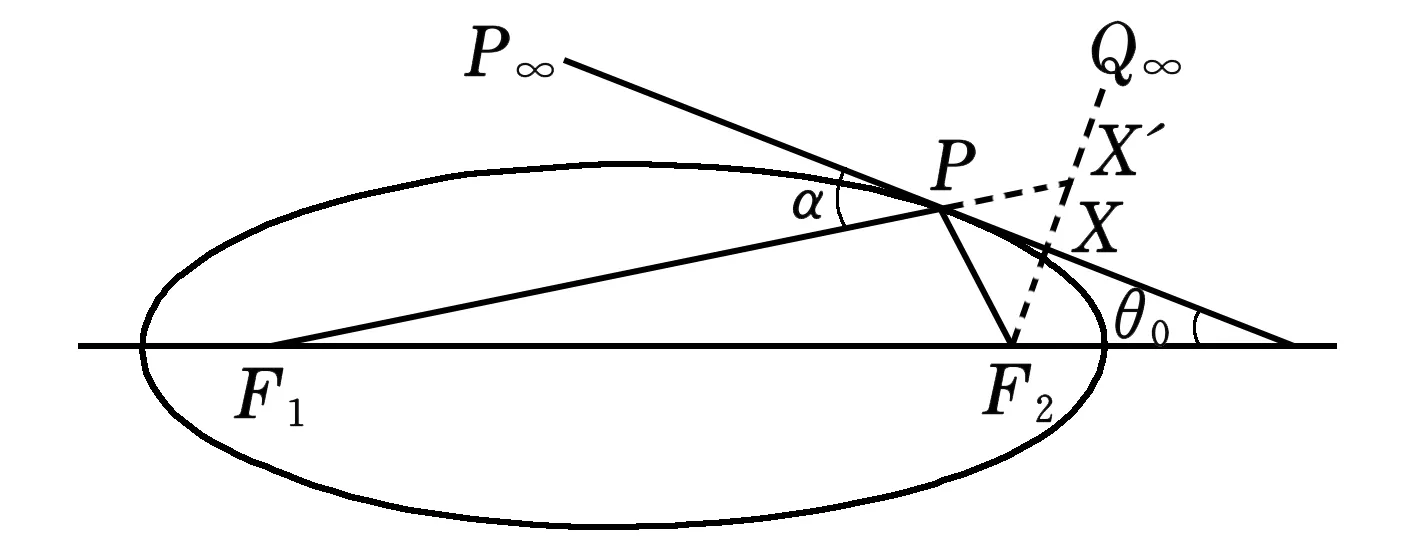
图3

P∞(P∞X，…)→F2Q∞(X，…)→F2Q∞(X′，…)→F1(F1X′，…).

首尾两个映射是线束与直线间透视，它们合成射影映射φ∶P∞(P∞X，…)→F1(F1X′，…).易知，φ(P∞F1)≠P∞F1，φ不是透视.由Steiner定理，φ的对应直线交点是一条二次曲线，此曲线过P∞与F1，F2(φ(P∞F2)=F1F2).由映射φ的构造，不难知道，φ(P∞Q∞)=F1Q∞.因此曲线过P∞，Q∞是一条直角双曲线.

对于φ给出的曲线上一点P，确定一个以F1，F2为焦点过P的椭圆.由椭圆焦点的光学性质及φ的构造，P∞P是此椭圆在P处的切线.φ给出的曲线是所求轨迹.设F1(-a，0)，F2(a，0)，下面推导新曲线的方程.

设PX的方向是cost0∶sint0，它的垂直方向是-sint0∶cost0.设X(a+tcost0，-tsint0)是F2Q∞上点，则X′(a+2tcost0，-2tsint0)，于是

它们的交点是新曲线上点.从前一式可得t=sint0(x-ycost0-a)，代入后一式得新曲线的方程

x2-y2-2xycos2t0-a2=0.

另法如图3，设过P的切线与椭圆对称轴的夹角是θ0=π-t0，PX与PF1夹角是α.易知，∠PF1F2=α-θ0， ∠PF2F1=α+θ0，它们的差是2θ0.反之，由∠PF2F-∠PF1F2=2θ0确定的P是此题轨迹中点，因此可以用上面性质1的方法讨论.

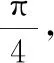
证抛物线在拓广平面上与无穷远直线相切，其对称轴(及所有的直径)过这一切点.取定一条性质中抛物线，图4画出了无穷远直线，设切点为C∞，这族抛物线的直径都过C∞.设P是抛物线上点，它的切线垂直于AB，P∞是此切线上无穷远点，C∞与P∞是相异两定点.设X=AP×BC∞，Y=BP×AC∞，对PPAC∞C∞B用 Pascal定理可得X，Y，P∞共线.因此，直线BC∞，AC∞之间以P∞为中心的透视把X变成Y.因而线束A，B之间把AX变成BY的映射φ是射影映射.易知，φ(AB)=BP∞≠AB，φ不是透视.由Steiner定理，φ的对应直线交点的轨迹是过A，B的二次曲线.

图4

另一方面，对于新曲线上的点P=AX×φ(AX)=AX×BY，过A，B，P与无穷远直线切于C∞确定一条抛物线.对此抛物线的退化内接六边形C∞C∞BPPA用Pascal定理可知，PP∞是P处切线，它垂直于AB.这证明新曲线是所求轨迹.

从上面讨论知道，由BC∞上点X可以作出新曲线上点P，下证新曲线是双曲线.易知，AC∞在φ下的像是BC∞，因此C∞是新曲线上点.设Q∞是AB上无穷远定点，如图 5可以作出P∞，Q∞，C∞的第四调和点T∞，R(P∞Q∞，C∞T∞)=-1.设X′=AT∞×BC∞，Y′=AC∞×BT∞，由第四调和点的作法可得X′，Y′，P∞共线.这说明φ(AT∞)=BT∞，T∞也是新曲线上点，这说明轨迹是双曲线.直线BC∞上点与双曲线上点有一一对应，图5上X′，C∞对应于双曲线上无穷远点T∞，C∞.

图5 图6

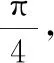
性质6设A，B是直角双曲线的两个顶点，P是直角双曲线上动点，则AP关于AB对称的直线与BP的交点在一个圆上.

证设P∞，Q∞是直角双曲线渐近线上的无穷远定点，过P∞，Q∞的直线互相垂直.如图7，设AP关于AB对称的直线与BP的交点是X.由Steiner定理，AXAPBP给出线束A，B间一个射影映射ψ∶AXBX，它的对应直线与无穷远直线的交点给出无穷远直线上一个射影映射φ.易知，ψ(AP∞)=BQ∞，ψ(AQ∞)=BP∞，因此，φ交换点P∞与Q∞， 这说明φ是一个对合.射影映射ψ把AA映射为BA，这里AA是A处切线.这证明对合φ有两对对应点给出的直线方向垂直，由[2] §4.4习题8，过对合φ的每一对对应点的直线垂直，因此射影映射ψ的对应直线都垂直.

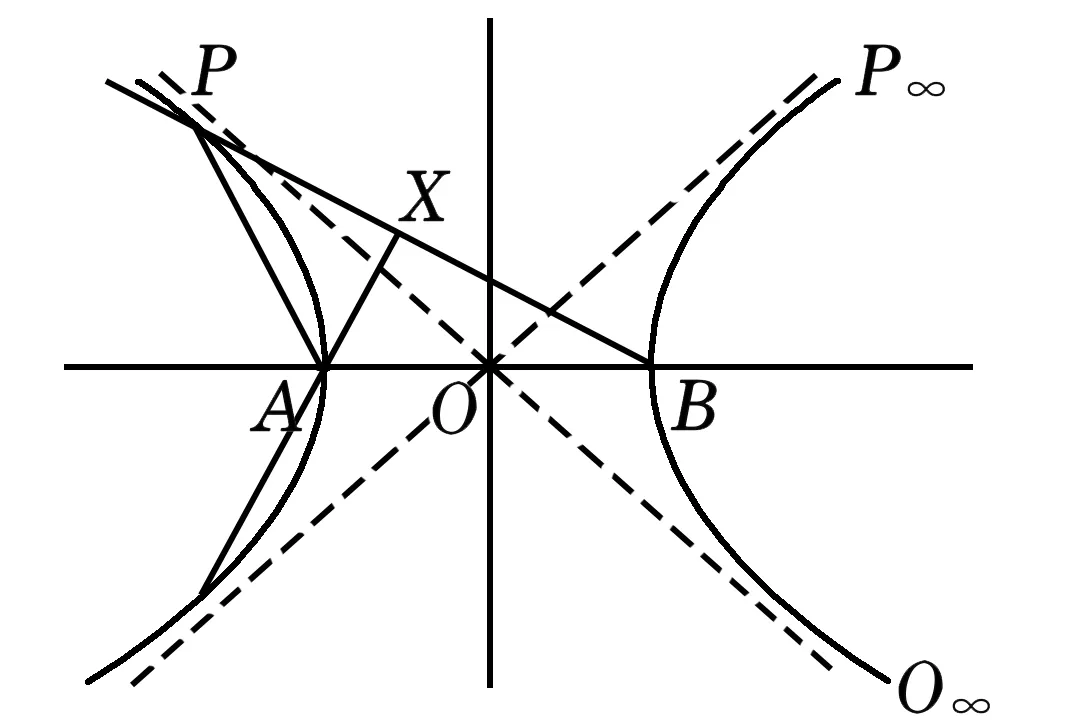
图7

这证明线束A，B间射影映射ψ的对应直线BX与AX的交点X在一个圆上.由Steiner定理，A，B也在这个圆上，这是一个以AB为直径的圆.

易知，XP给出了圆与直角双曲线的一一对应，圆与直角双曲线虚轴的交点分别对应于直角双曲线上无穷远点P∞，Q∞.

由 ∠PAB-∠PBA=∠AXB可知性质6可以看作性质1的一种特例.

下面的问题都可以用射影几何的方法解决，有兴趣的读者可以试试.

1. 设△ACB是锐角三角形，过边AB上点X向CA，CB作垂线垂足是Q，P.试求△CPQ垂心的轨迹.

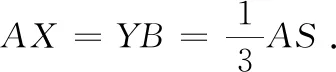
3. 设TP，TQ是圆锥曲线过P，Q的切线，一直线平行于TP交圆锥曲线于R，S，交TQ，PQ分别于L，D，则有LD2=LR·LS.

4. 设TP，TQ是圆锥曲线的切线，过切点P，Q的垂线交对称轴分别于D，E，则∠PTD=∠QTE.

5. 设AB，CD是二次曲线的平行弦，弦AC，BD所对曲线上点P，Q处切线分别平行于AC，BD， 则PQ也平行于AB，CD.

6. 设△ABC内接于椭圆，A与椭圆中心O的连线交椭圆于另一点Q，BC与Q处切线交于P，PO交△ABC的另两边于E，S，则EO=OS.

把题中椭圆改为双曲线，命题也成立.

7. 设△ABC与△A′B′C′内接于椭圆(或双曲线)，点E=AB×A′C′，S=AC×A′B′的连线与BC的交点P在A′处切线上，证明

(i) 下面六条直线交于一点：

AA′，BB′，CC′，ES， (B′C′×AB)×(BC×A′B′)， (B′C′×AC)×(BC×A′C′) ；

(ii) 六点A′B×AB′，A′C×AC′，BC′×B′C，BC×B′C′，AB×A′B′，AC×A′C′ 共线；

(iii) 直线B′C′，ES与A处切线交于一点.

8. 设圆内接△ABC的角A的平分线交圆于另一点D，对圆上任一点P，X=BP×AD，Y=AC×PD，证明XY平行于BC.

3 结 论

本文在直角双曲线可以由它的内接三角形的垂心生成的基础上，用射影几何的方法，借助Pascal定理、Steiner 定理，进一步给出一些直角双曲线的性质，说明它们可以用除了内接三角形的垂心生成外的其它方法生成.最后给读者列举一些有趣的几何问题，其用射影几何的方法比用平面几何方法处理更自然、条理更清楚.

致谢审稿人对本文的文字、公式以及排版提出了宝贵的修改意见，特别是摘要的修改更能体现本文的结论，在此表示衷心感谢.