行列式的几何意义及多面体体积的计算

何朝葵， 郑苏娟， 孙中喜

(河海大学 理学院，南京211100)

1 引 言

行列式作为线性代数中一个重要的基本内容，为了让学生深刻理解行列式的概念有学者在行列式教学中尝试了新的方法[1]，也有学者从有向体积的几何直观视角来探讨行列式[2].在一般的线性代数教材关于向量的混合积时，都会介绍三阶行列式的几何意义，那么对于任意一个n阶行列式，它是否也具有类似的几何意义呢？本文学习有限元方法中的面积坐标的概念[3]，引入体积坐标，利用多重积分证明了行列式和多面体体积的关系，从而解释了行列式的几何意义.

2 有趣的结论

结论1如果P0(x0)和P1(x1)为数轴上两点，令

则|D|=|x1-x0|=d(P0P1),即二阶行列式D的绝对值为数轴上点P0(x0)和P1(x1)之间的距离.

结论2若P0(x0,y0),P1(x1,y1)和P2(x2,y2)为平面上三个点，令

则三阶行列式|D|=2SΔP0P1P2,其中SΔP0P1P2为这三点确定的三角形面积.

结论3若Pi(xi,yi,zi)(i=0,1,2,3)为空间中的四个点，令

则

根据向量混合积的几何意义有|D|=V平行六面体=6V(ΩP0P1P2P3),其中V平行六面体为以P0Pi(i=1,2,3)为邻边的平行六面体的体积，ΩP0P1P2P3表示由这四点形成的四面体，V(ΩP0P1P2P3)为ΩP0P1P2P3的体积.

从以上三个结论，猜想

定理设Pi(xi1,xi2,…,xin) (i=0,1,2,…，n)为n维空间中n+1个点，令

则有|D|=n!V(ΩP0P1…Pn),其中ΩP0P1…Pn为n维空间中由这n+1个点两两连接所确定的n+1面体，V(ΩP0P1…Pn)表示这个n+1面体在n维空间中的体积.

证由于

消去L0,得

所以

=……

因而 |D|=n!V(ΩP0P1…Pn).

3 行列式的几何意义及多面体体积的计算

根据上面的分析，对于任意一个行列式

令P0(0,0,…,0),Pi(ai1,ai2,…,ain)(i=1,2,…，n),由于

则|D|可以理解为n维空间中由这n+1个点Pi(i=0,1,…，n)所构成的n+1面体体积V(ΩP0P1…Pn)的n!倍.利用行列式的几何意义可以求空间中多面体的体积，例如在空间中有如下一个多面体(图1)，其中各个点的坐标分别为

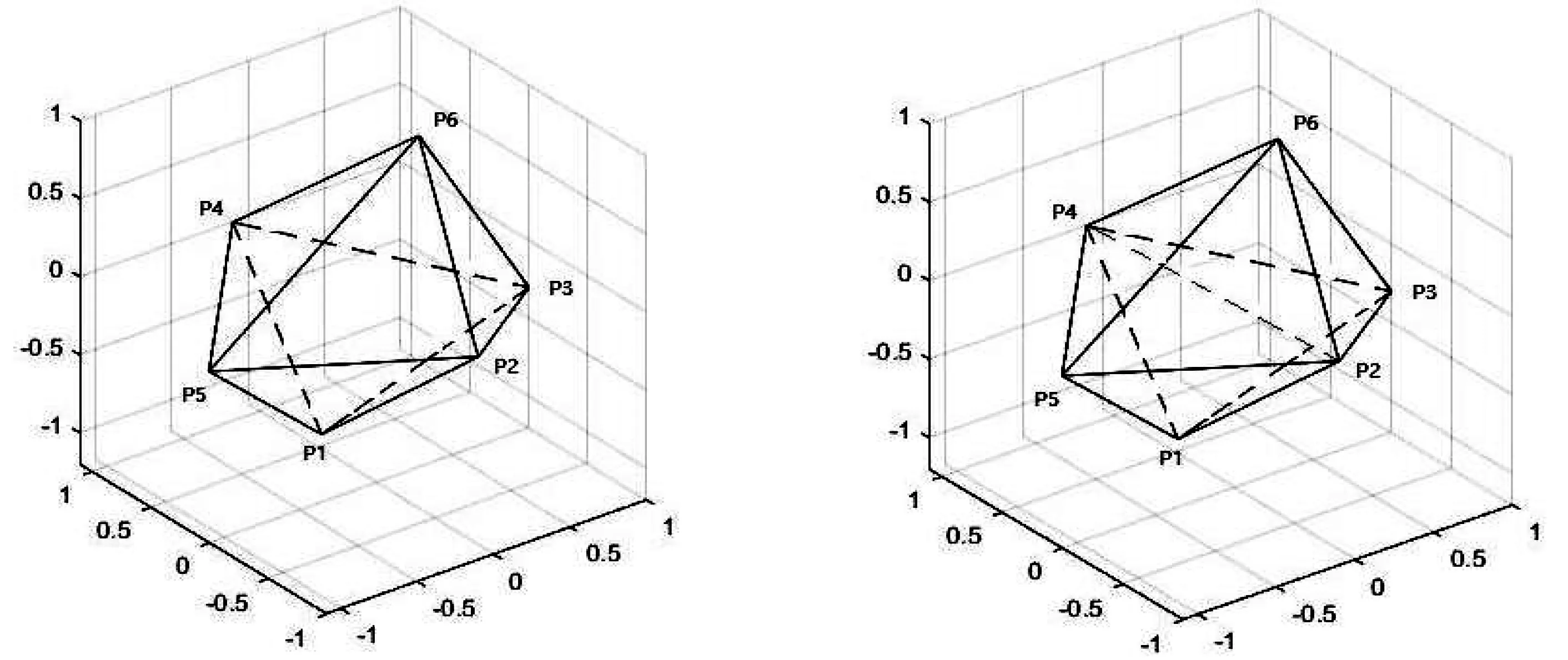
图1 图2

通过连接点P2和P4,把多面体分割成4个四面体(图2)：ΩP1P2P4P5,ΩP1P2P3P4,ΩP6P2P4P5,ΩP6P2P3P4, 由于

因此该多面体体积等于

V=V(ΩP1P2P4P5)+V(ΩP1P2P3P4)+V(ΩP6P2P4P5)+V(ΩP6P2P3P4)

5 结 论

对行列式的几何解释有助于加深对行列式概念的理解.对于空间中的一个多面体，可以利用剖分软件把多面体剖分成多个四面体单元，从剖分信息中提取每个四面体单元四个结点的坐标，就可通过行列式求得它们的体积，把所有四面体单元体积累加求和就得到多面体的体积，这很容易在软件上编程实现，如果多面体有边界面为曲面，则可对边界面部分剖分加密，从而得其体积的近似值.

致谢作者非常感谢相关文献对本文的启发以及审稿专家的建议.