一道2020年全国大学生数学竞赛题的多种推广

万安华

(中山大学 数学学院，广州510275)

1 引 言

高等数学是高校本科非数学类专业的一门重要基础课.教师如何在课堂教学中传授数学思想与数学方法是值得深入研究的课题[1].在高等数学的课堂教学中，选取富有启发性的例题进行适当的延拓，有利于培养同学们的创新思维能力[2]. 教师将每年的全国大学生数学竞赛试题及时引入相关章节的课堂教学中，并且通过综合运用数学方法将竞赛题进行多角度的延拓，不仅加强了例题的新颖性，也极大地激发了同学们的学习热忱.

2 分析与推广

引言中这道竞赛题中出现了两个底和指数互换位置的幂指函数[f(x)]g(x)和[g(x)]f(x). 对于一般的幂指函数u(x)v(x)(u(x)>0，u(x)不恒为1)，可将其转化为u(x)v(x)=ev(x)lnu(x)，由此来理解和处理幂指函数相关的数学问题. 当u(x)v(x)→1(在自变量x的某种变化趋势下)时，运用等价无穷小代换et-1～t(t→0)[3]， 可得

u(x)v(x)-1=ev(x)lnu(x)-1～v(x)lnu(x).

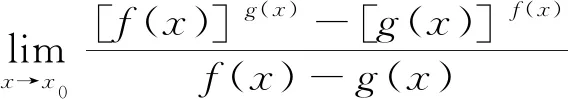
再进一步地推广为更加广泛的情形

因此只需考虑最后一种推广情形，前面的几种情形均可作为其特例而导出.其次，拟对幂指函数[f(x)]g(x)和[g(x)]f(x)的底作推广，可考虑一般的

综上分析，可将第一种推广思路和第二种推广思路结合起来，直接考虑包括了上述两种推广方向的一般情形

最后，还将考虑一般情形的

这一类型包括了

为特例，而此特例又包括了

为其特殊情况.

下面展开对上述几种推广情形的具体分析，并导出相应的结果.

2.1 对指数和底均作延拓后的一般情形

设f(x)，g(x)，Φ(x)，Ψ(x)，φ(x)，φ(x)在x=x0的某一邻域U内有定义，对任意x∈U，

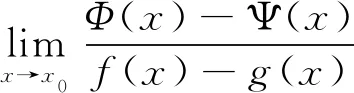
一方面

另一方面

因此

(1)

特例1设f(x)，g(x)，Φ(x)，Ψ(x)在x=x0的某一邻域U内有定义，对任意x∈U，

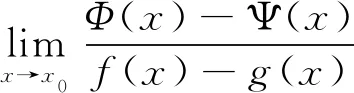
(2)

注1 引言中的竞赛题即为特例1在Φ(x)=f(x)，Ψ(x)=g(x)时的特殊情况，由(2)式即得

(3)

特例2设f(x)，g(x)，φ(x)，φ(x)在x=x0的某一邻域U内有定义，对任意x∈U，

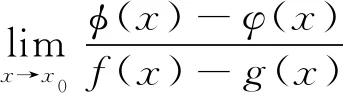
(4)

由特例2，可以得到下面的推论.

(5)

证由特例2，立即可得

因此

(6)

注2 作为(6)式的直接应用，却可以得到一个更一般的结论，即对于任意的实数λ≠(lna)-1，有

进一步地，还可以由特例2推出比推论1更为广泛的如下结论成立.

推论2设f(x)，g(x)在x=x0的某一邻域U内有定义，对任意x∈U，f(x)≠g(x)，且

4、整地改土：由于项目区为沙质土，土壤有机质含量低，需要对土地进行全面整治，通过人工施肥、深耕等措施，提高土地生产力。

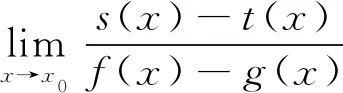
(7)

证在特例2中令φ(x)=[g(x)]s(x)，φ(x)=[f(x)]t(x)，则c=ad.由(4)式可得

因此

以下是推论2的几个特例：

(iii) 推论2 中当s(x)=fr(x)，t(x)=gr(x)(其中r是任意实数)时，首先由(4)式可得

接下来，由(7)式，立即可以得到

(8)

推论3设f(x)，g(x)在x=x0的某一邻域U内有定义，对任意x∈U，f(x)≠g(x)，且

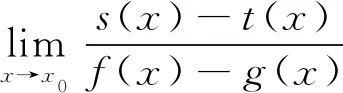
(9)

由推论3，立即可以得到以下结果：

2.2 推广到对数函数的一般情形

设f(x)，g(x)，Φ(x)，Ψ(x)，φ(x)，φ(x)在x=x0的某一邻域U内有定义，对任意x∈U，

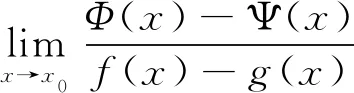
一方面

另一方面

因此

(10)

由上面的(10)式，立即可以得到以下特例.

特例3设f(x)，g(x)，Φ(x)，Ψ(x)在x=x0的某一邻域U内有定义，对任意x∈U，

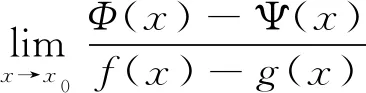
(11)

特例4设f(x)，g(x)在x=x0的某一邻域U内有定义，对任意x∈U，

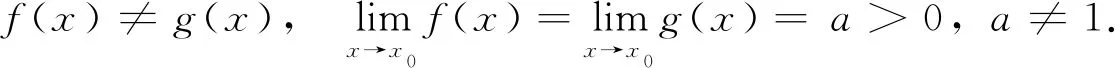
则

(12)

3 结 论

本文对最近第十二届全国大学生数学竞赛(非数学类)预赛中的一道试题从多个角度进行了延拓与纵深推广，拓展了教学内容.在高校数学课程教学中，恰当地引入与授课章节内容贴合的数学竞赛题，丰富了数学课堂的例题库.教学中对数学竞赛题进行延伸性改编，不但激发了同学们的学习热忱和积极参与竞赛的热情，而且帮助了同学们学会去发现新问题、综合运用数学方法解决问题，由此提升了创新思维与科研能力.

致谢作者非常感谢相关文献对本文的启发以及审稿专家提出的宝贵意见.