大学数学公共课程思政元素挖掘初探

赵东红， 魏海瑞， 刘 林

(北京科技大学 数理学院，北京100083)

1 引 言

为了深入贯彻落实习近平总书记关于教育的重要论述和全国教育大会精神，全面落实“三全育人”精神，2020年5月28日教育部印发了《高等学校课程思政建设指导纲要》.《纲要》指出，全面推进高校课程思政建设，把思想政治教育贯穿人才培养体系，将课程思政融入课堂教学建设全过程. 大学公共数学课程思政育人目标是注重数学思维方法训练和科学伦理教育，培养学生探索未知、追求真理、勇攀科学高峰的责任感和使命感，在向学生传授课程知识的同时，使其树立正确的价值观，激发学生科技报国的家国情怀和使命担当. 树立“课程思政”理念，强调学校教育应具备360度德育“大熔炉”的合力作用[1]，立足大学数学教学内容，将德育与数学基础知识融于一体，借助知识点、数学史、典故等，将知识传授与价值引领相结合，引导学生正确做人、做事和做学问，助力学生全面发展，报效祖国，实现“立德树人”之根本目标. 近几年，一线数学老师对数学专业课程进行了思政元素融入课程的研究——朱婧等[2]在《数学模型》将思政元素融入到传染病模型教学中，刘秀琴等[3]在《随机过程》将思政元素融入到马尔可夫链的讲解过程中，公徐路[4]以《离散数学》课程的思政教育为出发点，将德育元素合理渗透到专业知识中，郑苏娟等[5]以河海大学大禹学院《工科数学分析》这门课程为例研究了如何融入思政元素，提出了四要素，并将思政教育融于拔尖创新人才的培养体系中，取得了一定的成效，闵杰等[6]提出了《数值分析》课程思政建设的七个方面内容，并分别给出课程思政的教学案例. 同样，公共数学课程进行了融入思政元素到课程教学的研究—吴慧卓[7]以《高等数学》为例，阐述了课程思政的内涵，以实现从思政课程到课程思政的转化，孙和军等[8]结合数学学科特点和课程育人定位，设计切合实际的思政映射和融入点，选择合适的教学手段和方法，无痕地将思政元素融入课程教学. 但是，公共数学课程思政元素融入更偏重于理论描述，主要是在思政研究的必要性等方面.本文主要是从思政元素与实际案例的结合为出发点，研究公共数学课程思政元素融入，更加具体，更加直观，而且教学实践反映了以思政融入为契合点的教学内容更新，教学设计变化的成效.

最后设计科学的调查问卷，通过分析数据，可以看到在教务评价系统中，同学们对思政元素融于教学内容的反馈取得了令人满意的成效. 最终初步实现了适合各工科专业的公共数学课程内容重整，教学设计更新，人文教育渗透，把整个公共数学课程的教学质量提高一个台阶.

本文立足于思政微案例，对课程思政教学模式进行设计，但由于篇幅限制，只是对公共数学课程思政元素进行分析，分别对微积分、线性代数、概率论与数理统计挖掘思政元素，阐述并进行举例和初探.

2 主要内容

2.1 微积分课程思政元素挖掘并举例

以极限、定积分物理应用、常数项级数为例,详细地分析了思政元素的结合点，增强了数学学习的趣味性，实现借助合适的思政结合点帮助同学们树立正确的人生观和价值观.

思政微案例1极限——自然对数底e

金融复利问题：按年、半年、季度、月、周和天的顺序，计算一年后本息和，见表1.

表1 复利计息

(i) 继续按照小时、分钟和秒计息，假设计息周期趋于零，一年后本息会一直增大吗？

(iii) 引入e后,介绍历史上对e的研究过程[10]，约翰·纳皮尔找到了对数常数e；欧拉证明了e是无理数；夏尔·埃尔米证明了e是超越数.

无论是金融利滚利问题引入，还是对e的拓展学习，极大地提高了学生对数学的浓厚兴趣，同时让同学们更加理解，现在课本中学习的每一个知识点离不开一代代科学家不懈努力和刻苦钻研.

思政微案例2定积分物理应用——变力做功

设墙壁对铁钉阻力与铁钉击入深度成正比，铁钉长6cm，每次将铁钉击入1.5cm，如果铁锤每次击打铁钉时做功相等，铁锤击打多少次能将铁钉完全钉入?

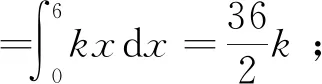
此例有助于同学们深刻理解习近平总书记的“发扬钉钉子的精神，一张好的蓝图一干到底”[11]涵义，实现培养学生学习和工作中要有专心致志和刻苦钻研精神的育人目标.

图1 变力做功

思政微案例3常数项级数——芝诺悖论

芝诺认为阿基里斯永远追不上乌龟，原因是：假设刚出发时，阿基里斯在A点，乌龟在B点，经过一段时间之后他到了B点，而乌龟却也往前走了一段到达了C点；阿基里斯又从B点开始追，等到达C点时，乌龟又往前走了一段，到了D点……总之，阿基里斯每赶到乌龟之前的落脚点，乌龟就已经往前走了一段，虽然它们之间距离永远在缩小，但他永远追不上乌龟！

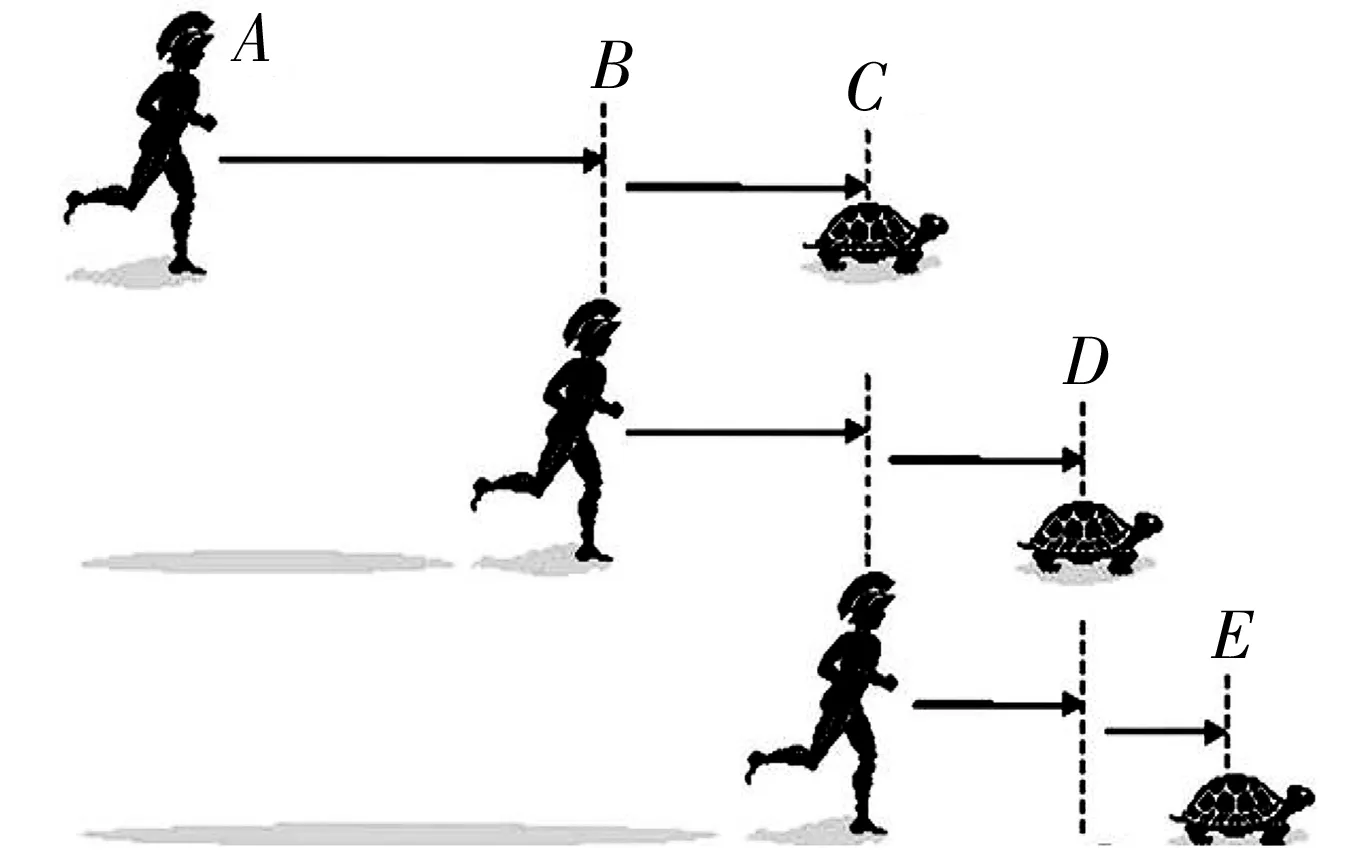
图2 芝诺悖论

芝诺悖论是缺少微积分这一数学工具造成错误理解，无法处理“无穷个无穷小”总和是什么.当每阶段考虑的时间越来越小，成为一个收敛的无穷级数，实际上证明了阿基里斯落后于乌龟的时间是有限的,并将在有限的时间内超过乌龟.

图3 液膜冷却问题

这个悖论对于锻炼同学们的数学思维有很重要的意义.芝诺悖论和其他逻辑学上有趣的悖论一次又一次地提醒哲学家和逻辑学家们去反思自己的思维框架和习惯，人类就是在这种反思和检讨中战胜错觉，取得进步.

表2 微积分思政元素挖掘举例

2.2 线性代数课程思政元素挖掘并举例

公共数学课中线性代数特点是公式多、式子大、符号繁琐以及规律性强，思政元素挖掘比较困难，下面以基变换与坐标变换、矩阵对角化、线性方程组为例，对思政元素进行分析.

思政微案例1基变换和坐标变换——液膜冷却问题

从中国航天卫星发射的历史进程引入，重点以长江二号火箭为例，介绍助推器发动机和一级主发动机的构成，引出液膜冷却问题.

这个实例既能形象直观地把基变换和坐标变换引出，又能激发同学们的爱国主义热情. 在引入过程中，同学们一起回顾了中国航天事业发展历程，充分肯定了祖国发展成就，增强了青年学生民族自豪感.虽然只是一节普通的数学课，但是很好地融合了思政材料，整个融入过程非常流畅，不但使同学们获得了数学知识，而且提高了思想境界，取得了一定的思政育人成效.

思政微案例2矩阵对角化——人口问题

假设北京市总人口是固定的，若每年有5%居民搬到郊区，3%郊区居民搬到市区，假设初始人口情况如下：40%居住在市区，60%居住在郊区，问10年、40年、60年后，市区和郊区人口比例如何?

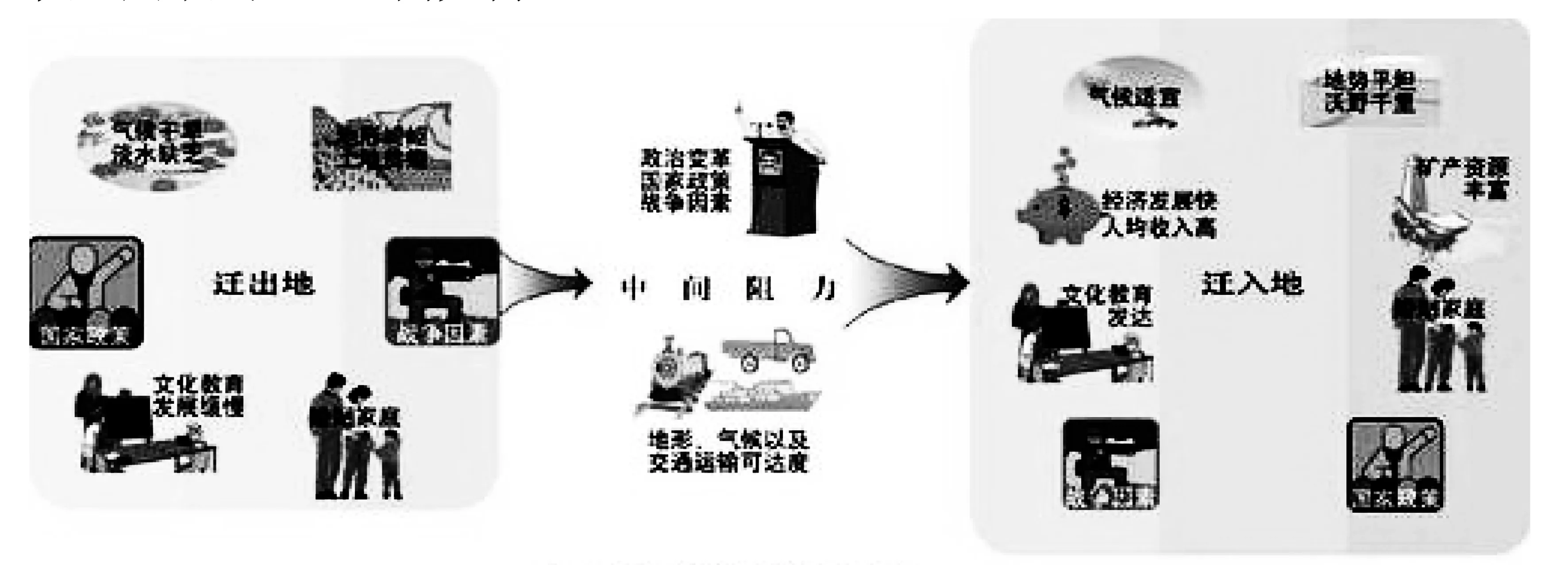
图4 人口迁移

作为开放式作业，通过矩阵对角化解决矩阵幂运算. 一方面有助于理解如何将抽象的知识点通过数学建模应用到实际问题中，另一方面引起同学们对城市问题、生态环境问题和人口迁移问题等社会问题的重视，引导同学们关注社会发展和民生问题，深刻理解新时代大学生历史使命和责任担当[12].

思政微案例3线性方程组——《九章算术》

《九章算术》第八章方程中介绍了一次方程组，采用分离系数方法表示方程组，这些系数相当于现在的矩阵. 解方程组使用的直除法与矩阵的初等变换一致，这是世界上最早提出的完整解线性方程组解法. 在这一章使用了负数，虽然负数是现在初一年级学习的内容，但在当时这是世界数学史上一项重大成就，第一次突破了正数范围，拓展了数字系统.

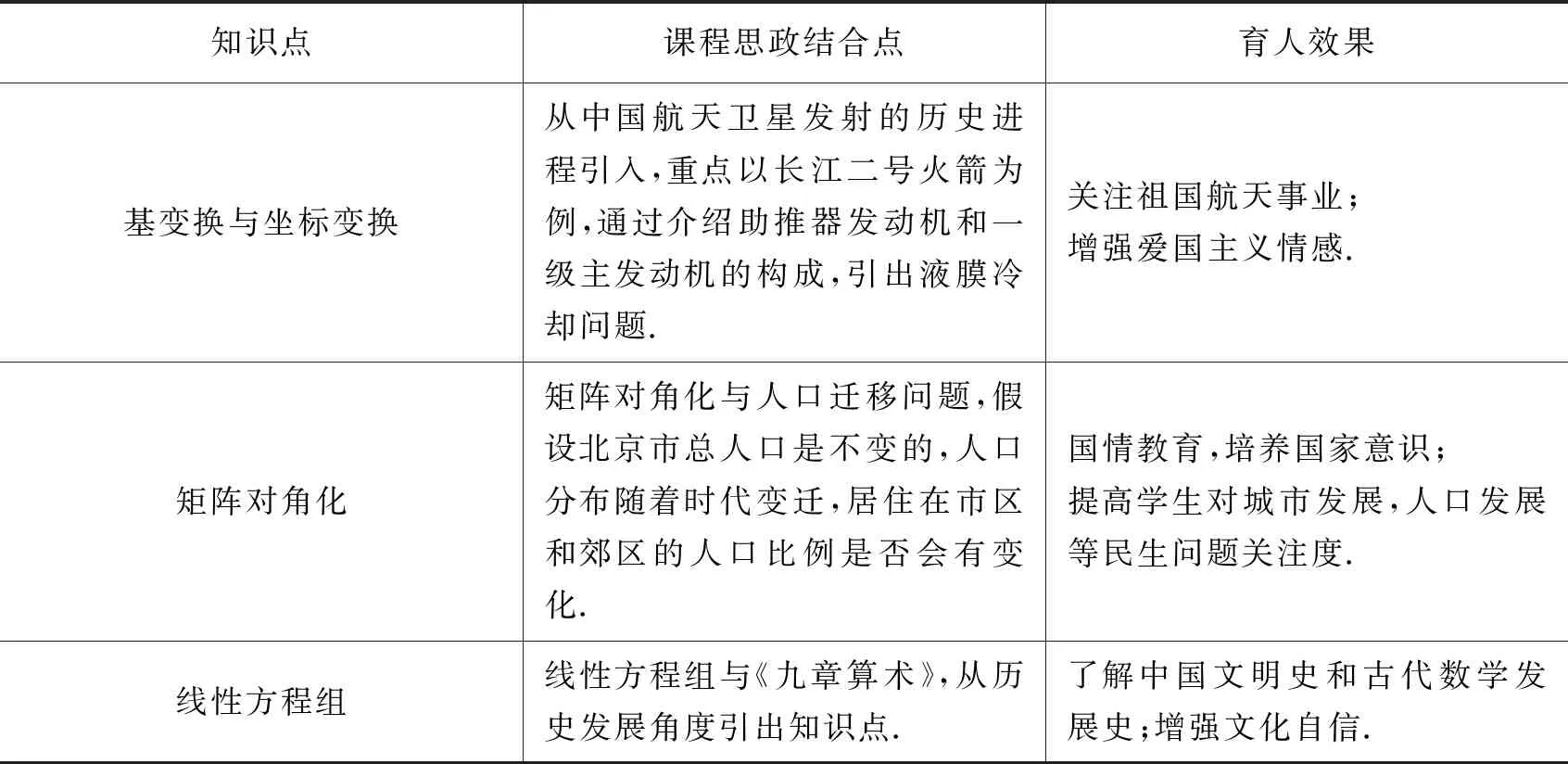
表3 线性代数思政元素挖掘举例

2.3 概率论与数理统计课程思政元素挖掘并举例

概率论与数理统计[13]相对于其他公共数学课程而言，跟实际问题结合最为密切，应用背景更丰富，本文从课堂教学挖掘的思政元素中，以数学期望、贝叶斯公式、假设检验为例进行分析.

思政微案例1数学期望——核酸检测分组

原问题：某地区共有1000人参加疾病普查，已知每人血液呈阳性的概率是0.2，采用两种方案进行血液检测.

方案1：逐一进行检测；方案2：每100人为一组进行分组检测，哪种方案最优？

新问题：某地区共有1000人参加新冠病毒核酸检测，已知每人咽拭子呈阳性的概率是0.2，采用两种方案进行核酸检测.

方案1：逐一进行检测；方案2：每100人为一组进行分组检测，哪种方案最优？

这一背景变化结合了当前实际环境，本质上是同一个数学问题——数学期望，不同的是给我们提供了非常好的思政育人条件，在课堂教学中计算出结果之后，设计了一个分享最近一年感受的环节，可以看出每个同学不但学业上取得进步，思想上更加成熟.

思政微案例2贝叶斯公式——警察破案

某地发生了一个案件，嫌疑人有甲、乙、丙三人，在不了解案情细节(事件B)之前，侦破人员根据过去的前科，对他们作案可能性有一个估计，设为P(A1)、P(A2)、P(A3),且P(A1)最小，但在知道案情细节(事件B发生)后，这个估计就变为P(A1|B)、P(A2|B)、P(A3|B),但P(A1|B)最大. 原来认为作案可能性较小的甲，现在变成了重点嫌疑犯. 通过这个引例，不但加深理解贝叶斯公式的本质，而且间接地教育同学们要成为一个遵纪守法之人.

思政微案例3假设检验——女士品茶

这个故事最早出现在统计学家Fisher发表于1935年的著作《The Design of Experiment》，被用来描述原假设.统计学家Fisher在当年就给出了他的一套实验方法：他调配出了八杯其他条件一模一样而仅仅是倒茶倒奶顺序相反的茶，让女士品尝之后告诉他哪四杯是先倒“奶”.

首先假设女士没有这个能力(被称为原假设)，如果女士很好地鉴别了这八杯茶，那就说明在原假设成立的情况下，发生了非常反常的现象，以至于说明原假设是令人怀疑的.从统计上来说，如果在原假设成立的前提下，发生了非常小概率的事件，有理由怀疑原假设的真实性.这也是Fisher教授的假设检验的基本思路-概率性质的反证法.

这个故事作为开端，可以让同学们理解，每一个科学理论的诞生都是来源于生活，来源于实践，而且从中可以看到科学研究的这种精神，学习科学家善于观察，善于对生活中的每一个细节进行思考、反思和试验.

表4 概率论与数理统计思政元素挖掘举例

3 教学效果与教学评价

3.1 教学效果

为了检验教学效果，学期末对微积分、线性代数两个讲台同学进行了课程思政调查问卷.调查问卷设计了四个评价指标，分别为价值引领的作用、爱国主义与文化自信、科学创新的精神、中华民族精神，评价等级为非常有效、一般有效、无效三个层次. 微积分讲台人数151人，其中140人自愿参加了调查问卷，线性代数讲台人数180人，其中170人自愿参加了调查问卷，调查结果如图5、图6所示.

图5 微积分课程思政调查数据饼图 图6 线性代数课程思政调查数据饼图

实践表明，绝大多数同学对思政元素融入到课堂教学中是肯定的，正如高教司司长吴岩所说让课程思政成为有情有义、有温度、有爱的教育过程. 同时说明了将思政元素融于公共数学课程内容这种教学模式值得研究和探索，我们将在今后的教学中继续应用与改进.

3.2 教学评价

学校为落实《关于进一步加强课程思政建设的实施意见》(校党发〔2020〕37号)文件精神，开展“课程思政特色示范课程”建设工作. 学校整个评教体系导向发生很大变化，评价内容如下：

将课程思政融入到课程教学中，提高了对学生人文关怀的程度和同学们对公共数学课程的学习兴趣，可以看出学生对教师各方面评分较高，特别对课程思政有效性评价较高. 下面我们对表5中微积分讲台和线性代数讲台第2题和第7题进行详细地分析，如图7—图10所示.

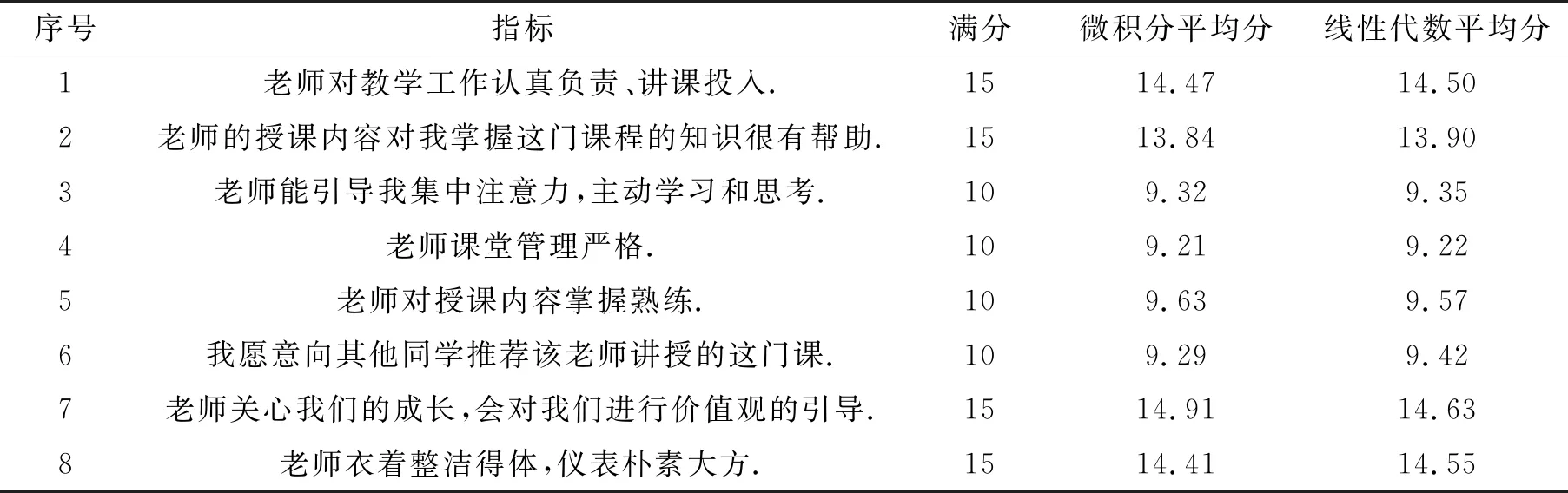
表5 教学评价指标数据

图7 微积分讲台 图8 微积分讲台

图9 线性代数讲台 图10 线性代数讲台

从上述分析中，可以看出融入了思政元素的公共数学课受到了学生认可和喜爱，但也看出个别同学觉得思政元素与课程内容融合度比较弱，说明后面我们要继续努力挖掘思政元素，实现传授知识与思政元素无缝对接，达到润物细无声的教学效果.

4 结 论

本文对三门公共数学课程思政元素挖掘并初探，从多个角度深入分析，通过丰富的教学案例说明如何将思政元素融入到课程教学中.实践证明，公共数学思政特色示范课建设的必要性和有效性. 众所周知，提高同学们对公共数学课程学习兴趣和培养创造性思维能力是教学目标之一，现在我们更加注重如何将知识传授，能力培养和价值引领有效结合，将隐藏在课程内容中的思政元素挖掘出来，不但激发学生的学习兴趣，而且使学生具有多方面的情感、态度和价值观，全面提升育人质量，最终实现立德树人之根本目标.

致谢非常感谢参考文献对本文的启发，审稿专家认真评审了论文，提出了宝贵的意见，作者受益匪浅，在此表示衷心的感谢.