基于Java Map的素数方阵求解优化
2021-07-08雷育铭
雷育铭
(清远职业技术学院信息技术与创意设计学院,广东 清远 511510)
1 引言
在基于Java集合类求解素数方阵的过程中[1],笔者发现:以HashSet为例,方阵阶数每增长一阶,在同一环境下算法运行时间增长10倍以上。就1亿个组合测试时间来看,7阶的运行时间超过15小时,如下表所示:
其中,A集合包含所有N位的可逆素数,B集合为A集合中不包含偶数和5的所有素数。
为了解决此问题,笔者通过精简集合样本数、从数字拆分中删除new操作、加快方阵旋转、使用映射替换集合以及检测与消除无效组合等手段,对引文[1]中的算法进行了大幅优化,最终使得运行时间在7阶时能够缩短2200多倍,降为23秒左右。
2 精简集合样本数
N阶素数方阵的求解,基本思路是先取样组合后枚举测试,主要规则、步骤为:①筛选N位可逆素数构成A集合,在A集合中继续筛选不含偶数和5的可逆素数构成B集合;②循环从B集合取两个不同的素数分别放首尾两行,从A集合取N-2个不同的素数放中间的N-2行,组合成初始方阵M;③判断方阵M是否为目标方阵(即M的各列和两条对角线任意方向上的N位数均构成一个N位可逆素数),如果不是,则返回②;④判断M是否与已有的目标方阵相似,如果是,直接返回②;⑤如果不是,则添加M到目标方阵集合,返回②。流程如下:
经过观察分析,B集合中的可逆素数是成对存在的,比如4位可逆素数1193和它的逆序素数3911同时存在。考虑到每个目标方阵同样具有方向可逆性[1],因此可以规定M的首行只需从B集合每对互逆的素数中的较小者中取样即可,这些较小者构成的集合记为C集合。
至此,方阵M的各行取样组合方法如下:
仅此一步优化,算法步骤③需要检测的样本总数就缩减了一半,对缩短算法的运行时间起到了积极作用,比如4阶可以缩减近半。但随着阶数的增长,缩减越来越不明显,没有带来数量级的改变。
3 从数字拆分中删除new操作
为了判断方阵M的各列和对角线是否构成可逆素数,需要先把M的伴随数组MA中的各个素数按位拆分成单个数字,初始代码如下:

作为对比,笔者将局部数组a改成类静态成员对象,即a只需new一次,然后对比了两个版本的运行时间:
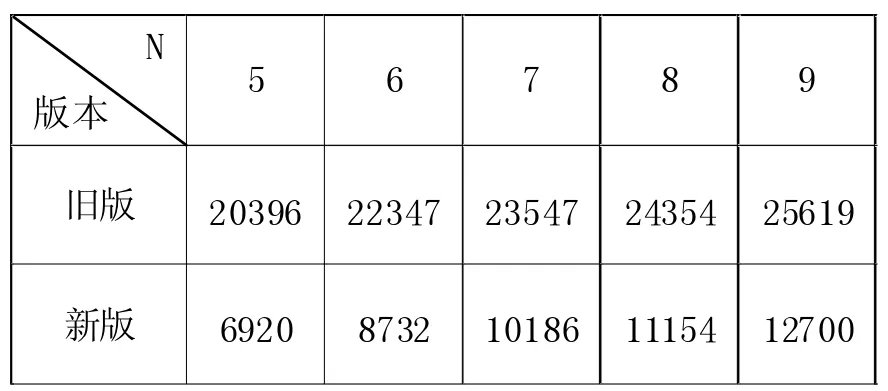
表2 1亿个N位数拆分时间对比(单位:毫秒)
由此可见,new操作对数字拆分方法的运行时间具有明显影响。在相同样本数的情况下,每次分配一个一维数组来保存结果,相比使用共享数组,会使得运行时间翻倍。对比表1中的数据,可以看到这个改进节省的时间,相对总体时间而言也不是关键的。

表1 4~8阶运行时间对比
4 加快方阵旋转
受上一步的启发,在判断M是否与现有目标方阵相似时,笔者对原来的旋转方法进行了优化,即使用类静态数组成员代替每次都要new的局部数组,从而减少了步骤④运行的时间。具体代码如下:

因为满足要求的目标方阵数量有限,因此,此次优化效果不明显。
5 使用映射替换集合
考虑到步骤③中每一次取样组合成新方阵M后,都需要对各个素数进行拆分。分析显示,该步骤产生的组合数量是巨大的[1]。结合“3从数字拆分中删除new操作”的测试结果,笔者决定将数字拆分操作提前到步骤②来完成,即修改构建A、B、C三个集合的过程,在找到符合要求的素数时,顺便就把它们按位拆分成一维数组,再以该素数为Key,以<K,V>对的形式保存到相应的HashMap映射mapA、mapB、mapC中。在步骤③需要按列和对角线组合新N位数时,直接从相应映射中以素数为Key提取预先拆分好的Value数组即可。从A映射构建B、C映射的代码如下:

经此优化,测试算法在N取值4~8时的运行情况,速度在之前几步优化的基础上,再提升了10~30%,但没有发生数量级的改变。
6 检测与消除无效组合
深入分析图2不难发现,为了满足素数方阵的要求,需要检测取样自A映射的N-2个素数和取样自B、C映射的两个素数是否有重复。如果存在重复,则组合无效,需要进行下一轮取样。只有检测通过,才进行图1步骤③④中的操作,代码如下:
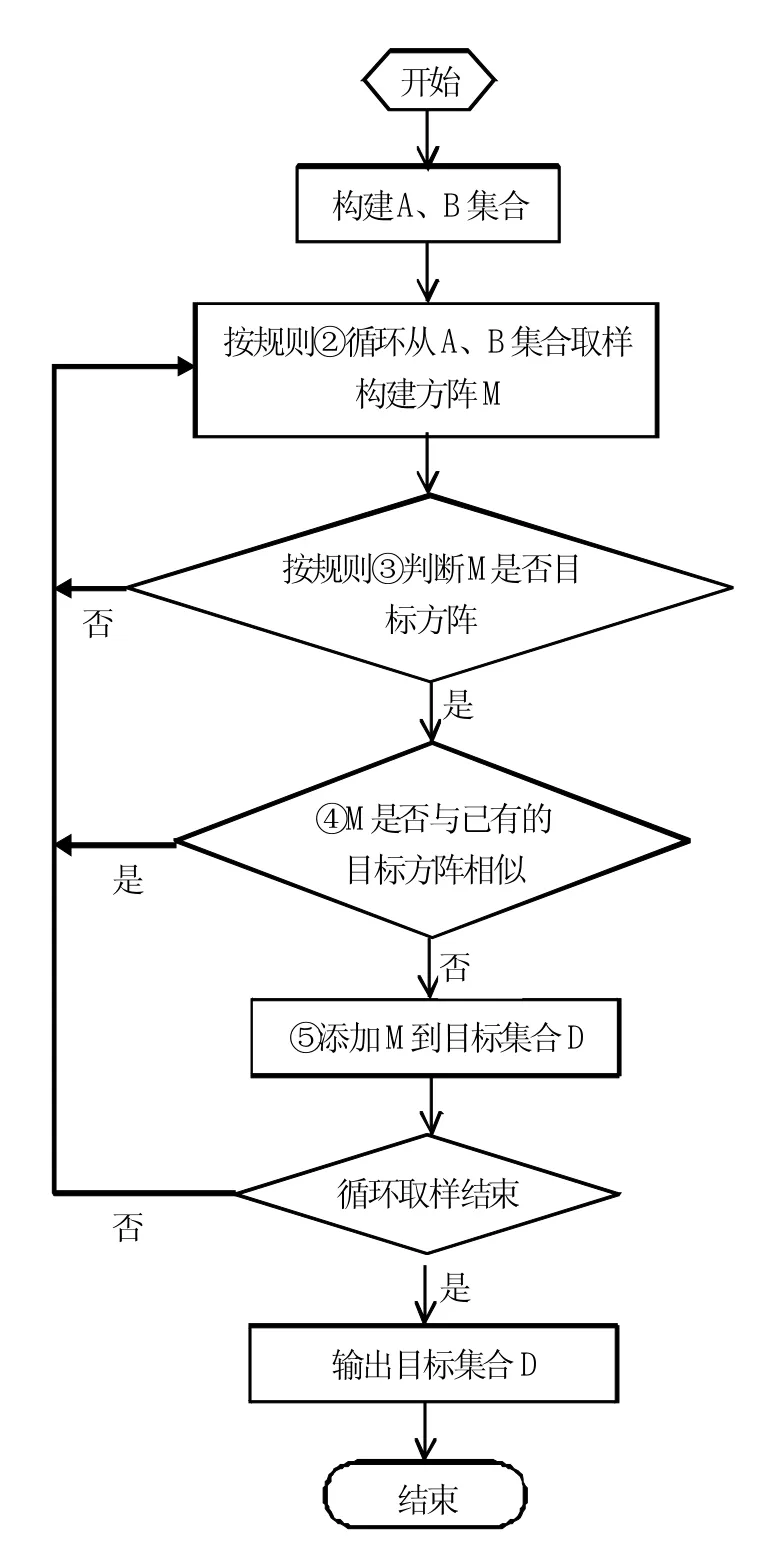
图1 素数方阵求解流程图

图2 方阵各行取样组合方法

上述代码能够有效检测无效组合。当检测到无效组合后,通过迭代跳过。经过仔细分析,不难发现这样做的效率是非常低的,这也是算法运行时间随着阶数增长大幅飙升的根本原因。如图2所示,取样迭代从最后一行——即B映射——开始。也就是说,刚开始的时候,中间N-2行样本必然是相同的。假设A、B映射样本数分别为S1、S2,为了满足方阵组合要求,程序需要执行T=次空迭代,即从第二行开始,依次取A映射的第1、第2...第N-2个元素,才能使得中间N-2行处于互不相同的初始状态。当N=7时,!这就是算法运行超过15个小时仍未检测到1亿个有效组合的原因。为更高效率地消除无效组合,在循环取样开始前,中间N-2行应该步进式地错开,以确保它们互不相同:

后续的迭代过程中,在检测到重复样本后,应该就地迭代,而不是从最后一行开始迭代。根据此思想,优化后的代码框架如下:



经过此优化,各阶运行时间都有大幅缩减,第一个目标方阵出现的组合数均有下降,更重要的是,从6阶开始算法运行时间发生了数据级的缩减,阶数的增长不再对运行时间构成数量级的影响,如下表所示:
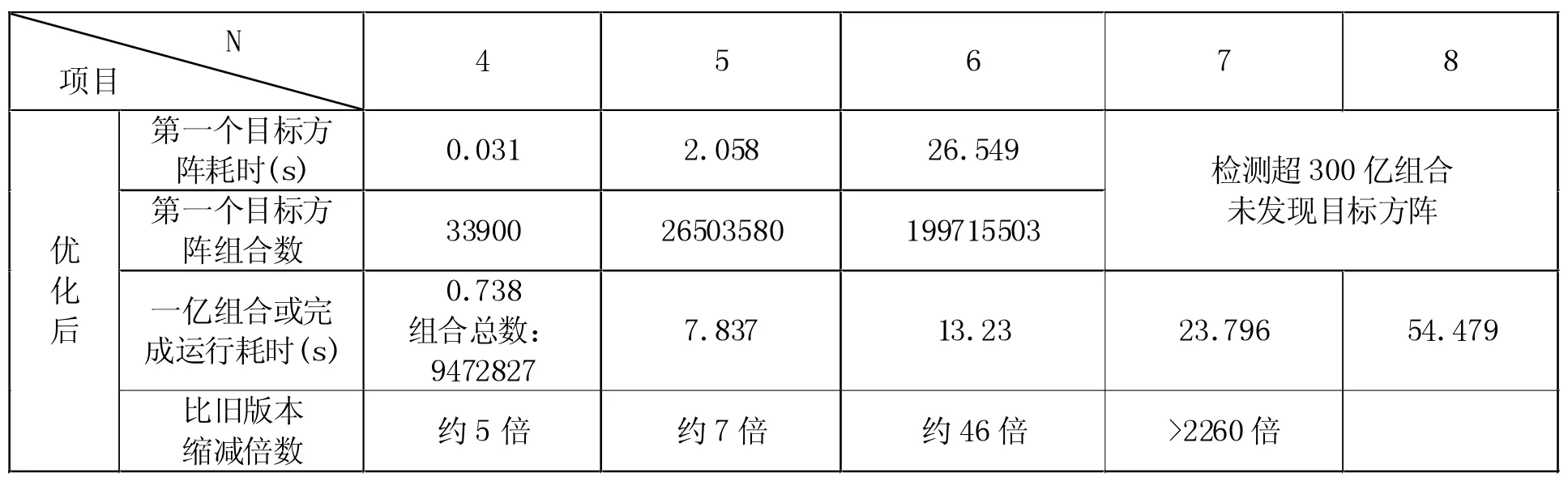
表3 优化后4~8阶运行时间对比
