聚焦数学思维 优化解题策略—复习阶段如何讲题

广东省佛山市顺德区聚胜小学 郭利锋

“讲题”顾名思义就是“讲解习题”或“习题讲解”。“讲题”教学是小学数学教学中重要的内容，也是教学难点之一，尤其是到了复习阶段，讲题教学就显得尤为重要。目前讲题教学主要存在以下几方面的问题：（1）就题讲题，教师貌似讲解细致，但问题呈现单一线性化，缺乏知识的整体性、关联性、灵活性，也缺乏解题方法和策略的总结提炼、反思迁移；（2）题海战术，教师采用“以量取胜，以多胜少”的方式，通过大量刷题让学生在题海中漫无目的“熬游”，师生甚是煎熬；（3）缺乏重点，把习题从头到尾讲一遍，没有侧重点，面面俱到，平均用力，费时费力；（4）常讲常练常错，不重视练习课的备课，缺乏对错题、拓展题的研究，过分依赖辅导资料或凭经验、凭感觉走；（5）自我陶醉式，教师侃侃而谈，一讲到底，缺乏对学生实际情况的分析与研究，不能从学生的视角设计教学内容和选择教学策略，学生游离在教学之外，师生貌合神离。基于以上种种原因，使得目前讲题教学效率低、效果差，教师们经常在“恨铁不成钢”的情绪下“呕心沥血”一遍一遍地讲解。学生们呢？也在“悔恨自责”或“漠然抵触”的情绪下一次一次“听题”，这样的“剧情”总是重复上演。

笔者认为，造成讲题教学的这种现状，首先是教师缺乏数学学科理论高度，缺乏系统观点和结构思维，不能从“统整”的角度研究和编制习题，习题思维价值不高，教学功利短视，讲授的知识碎片化；其次是教师在讲题教学中缺乏解题方法和策略的指导和优化，更谈不上数学思想方法的渗透和提升了。因此，笔者认为具体应从以下两个方面进行“讲题”教学：

一、聚焦数学思维、精心编制题组

数学思维是数学能力与数学素养之“魂”，教师要放飞学生的数学思维，打造智慧的数学课堂，引领学生走入数学的“灵魂深处”。因此在讲题教学中，设计好思维含金量高的习题是最关键的。要用统整的思维，着眼于一个知识板块或一个单元，或一类有关联的知识点，通过选编、改编和创编，将题目形式类似、解法可以类推、思维层次逐步深化的题目串在一起构成题组进行训练。这样的题组训练具有鲜明的对比性、层次性、迁移性，对培养学生数学思维、提高解题能力发挥了重要作用。

讲题教学范例一：

（1）下面三个图形的面积相等吗？这三个图形的面积大小有什么关系？

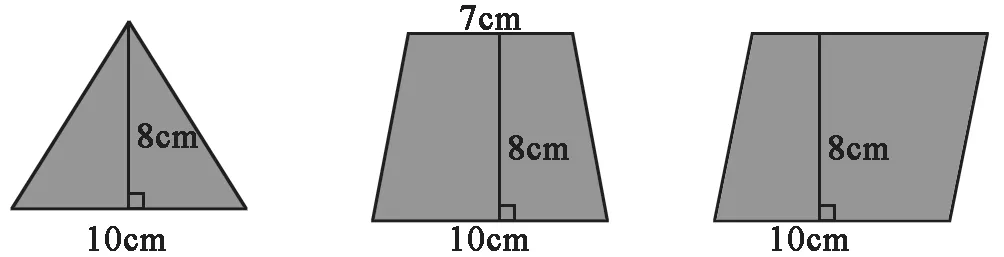
学生通过计算很快得出结论：S平＞S梯＞S三。

追问1：不通过计算，能得到这个结论吗？说说你的理由。

学生在独立思考和讨论交流的基础上，教师运用课件动态展示：

①以梯形为标准，梯形的下底不变，当上底逐渐变小，直到上底为0时，梯形就变成三角形了，因此三角形面积比梯形的面积小。

②以梯形为标准，梯形的下底不变，当梯形的上底逐渐变大，直到上底和下底一样长时，梯形就变成了平行四边形（或长方形），因此平行四边形的面积比梯形的面积大。

追问2：你能说一说这三个图形的面积计算公式之间有什么关系？

以上解题的过程中，通过引导学生想象或课件动态显示，让学生直观感受到图形之间的相互转化和面积大小的变化，明晰了三种图形面积之间的关系：三角形、平行四边形（长方形、正方形）、梯形都可以用同一个公式，也就是梯形的公式。其共同的本质是：这些图形的面积就是“底与高的乘积关系”。这样就把这几种图形的面积公式整体沟通，打通联系，好理解、好记忆（见下图）。

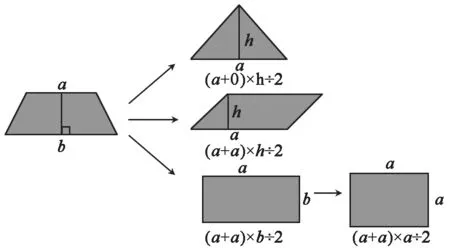
这时再引导学生运用得到的结论（统一成梯形的公式）进行验证，分别计算三个图形的底，三角形的底：（0+10）÷2=5cm，梯形的底：（7+10）÷2=8.5cm，平行四边形的底：（10+10）÷2=10cm。通过比较得出判断：当三个图形的高相等时，因为α平＞α梯＞α三，所以S平＞S梯＞S三。

（2）把下面的梯形剪拼成一个平行四边形（如下图）。

①求平行四边形的底。

解法一：先求梯形的面积：（6+8）×4÷2=28（cm2）

再求平行四边形的底：28÷4=7（cm）

解法二：（6+8）÷2=7（cm）

②如果在这组平行线之间画一个三角形，高和面积都与梯形、平行四边形相等，这个三角形的底要画多少厘米？6+8=14（cm）或7×2=14（cm）。

这个环节通过习题解法的开放，引导学生积极思考和辨析，交流和碰撞，达到对结论的验证和运用，促使学生对三种图形面积公式之间的联系有了更深刻的理解和思考，在解题时运用这种知识的关联灵活解答，达到深度学习和思考，可以进一步培养学生数学思维。

讲题教学范例二：

（1）面积是10cm2的平行四边形有（ ）个。（底和高都是整厘米数）

A. 2 B. 4 C. 3 D. 无数个

很多学生认为是4个，因为10=1×10=2×5，这时教师不表态，接着出示下一题：

（2）下列平行四边形的面积是否相等？为什么？

学生看后恍然大悟，正确的答案应该是“无数个”。运用“数形结合”直观易懂，达到了“此时无声胜有声”的效果，并由此得到结论：等底（同底）等高的平行四边形，面积相等。接着类推到三角形中是否也有类似的规律呢？

（3）下列三角形面积是否相等，为什么？

学生很快得出结论：等底（同底）等高的三角形，面积相等。

（4）下列几个图中的阴影部分面积是否相等？为什么？这样的三角形有多少个？

学生类推很快得出结论：阴影部分（三角形）的面积都相等，且是平行四边面积的一半，因为这些三角形等底等高，这样的三角形有无数个。

（5）右边图形中阴影部分面积等于平行四边形面积的一半吗？为什么？

大部分学生凭直观猜想：阴影部分的面积是平行四边形的面积的一半。至于为什么并不能说出道理来，这时电脑显示：

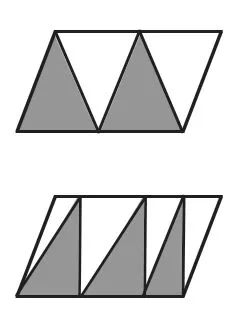
通过动态、直观对比变化前后两个图形，总结规律：阴影部分的面积等于平行四边形面积的一半。

（6）独立解答：求下图阴影部分的面积？

部分学生还是按照常规的思路解答，用“S梯－S三=S阴”，也有部分学生能运用上面的结论进行迁移学习，求阴影部分的面积可以转化为直接求大三角形的面积（见下图）：12×4÷2=24（cm2）。

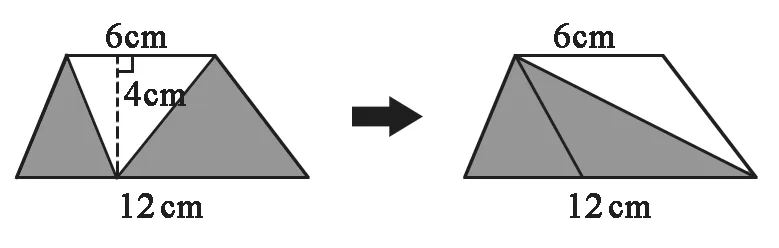
教学至此，教师还要引导学生纵观题组进行对比分析与思考：这几道习题的内在关联是什么？学生通过观察、辨析、讨论、总结，明晰这几道题隐含的条件:“平行线之间的距离（高）处处相等”，得出结论：等底（同底）等高的平行四边形（三角形），面积相等。这个题组就是围绕这个数学知识模型进行改编、创编和拓展运用的，学生们只要能善于抓住这一数学模型的本质意义去理解和变通，题目就能迎刃而解。这样讲题一方面沟通了不同图形之间的本质联系，使学生不断积累的点状零散知识通过“本质关联”串成线、结成网，使知识系统化、结构化，并加以内化，另一方面也培养了学生系统的观念和转化的思维，拓宽思路，促进学生数学思维立体化发展。

教师只有真正做到了对习题的深度研究和精心编制，课堂上才能真正实施“深度教学”，学生也才能真正做到“深度思考”，即能够通过题组训练促进学生数学思维的发展、能力的提升、素养的提高。

二、优化解题策略，渗透数学思想

“策略”即计策和谋略，是人们在面对具体问题时做出的基本判断和产生的基本解决思路。体会策略价值、提升策略应用意识、感悟数学思想方法是讲题教学重要的教学目标之一。习题是静态显性的，而思维是动态隐形的，如何让数学思维可视化、条理化、结构化，是要讲究方法和策略的，教师要鼓励和提倡学生解题策略的多样化，并尊重学生在解题过程中表现出来的对不同策略的应用水平。例如，上述两个讲题教学范例中就渗透了数形结合、迁移转化、建立模型、推理归纳、化繁为简、类比联想等解题方法和策略。

同时，在讲题教学中，对“解题的方法与策略”的理解应上升到其所蕴含的数学思想（意识、理念）层面。数学思想方法不是生搬硬套、从外部硬塞给学生的，而是要引导学生在数学知识发生发展和解决问题的过程中逐步体悟到，并在反复渗透和应用中加深理解和掌握的。因此在讲题教学中，教师需要及时引导学生进行反思和回顾：（1）解题的关键是什么？通法（模型）是什么？（2）运用了哪些解题的策略？这些策略在以前哪些知识的学习中运用过？这个环节必不可少，不可忽略。通过回顾总结解题的思路和关键所在，提炼并检视策略的运用，有利于领悟解题方法和策略适合的问题特征，促进解题经验迁移转化，提升学生的解题能力。当然，我们教师也需要进行深入思考和自我反思：这节课中培养学生哪些能力和素养？渗透的数学思想方法是什么？以上几个问题的解决过程，就是培养学生数学思维的过程。

三、讲题教学应注意的三个问题

在讲题教学中，除了要设计好思维含金量较高的练习题和渗透解题的策略与方法，还需要站在学生的角度思考讲题教学实施过程的有效性。

1.自主探究，展现过程

要让学生自己去发现、探索、解决，经历解题的整个过程。解题实际上是学生运用已有的知识经验与数学问题之间建立联系，并运用数学知识和数学模型解决新的数学问题的过程。学生在解答时需要调动多方面的知识，对学生来说具有挑战性，也有一定的难度，教师要有静待花开的心态，要给学生时间和机会，让学生灵动的思维过程充分展露出来。

2.问题驱动，深度思考

教师的任务不是“讲”，而是“问”和“引”，教师作为参与者和引导者，要做到含而不露、指而不明，以设问（大问题、关键问题、追问）调控探索的方向，将问题问在重点处、困惑处、关联处，有效激发学生思维能力，引导学生进行全面、深入的思考，并在与同伴进行交流思辨中得到启发和帮助。在练习完成之后，能从整体上建立知识之间的联系，形成结构化的思维方式。

3.回顾总结，提炼迁移

教师应着眼于学生可持续发展的能力与素养的提升，对在解题过程渗透的数学思考方法和解决问题的策略进行总结提炼，让学生掌握解决一类问题的“通法”，达到举一反三、触类旁通的效果。

培养学生数学思维能力、形成策略意识、提高解题能力，这是一项长期的、艰苦的、细致的教学任务，需要低、中、高年级的任教老师共同努力，将数学思维渗透在每节课、每道题中。讲题教学中要激发学生探究的欲望，激活学生的数学思维，引导学生多经历、真参与、敢尝试、会运用，能从联系的视角系统地思考问题，合理选择解题的方法和策略，提高学生解题的能力，进而提升学生的数学素养。