带中介轴承的双转子系统振动耦合作用评估

王杰，左彦飞,*，江志农，冯坤

1. 北京化工大学 发动机健康监控及网络化教育部重点实验室，北京 100029

2. 北京化工大学 高端机械装备健康监控与自愈化北京市重点实验室，北京 100029

3. 中国航发动力所—北京化工大学 航空发动机振动健康监控联合实验室，北京 100029

现代燃气涡轮发动机广泛使用带中介轴承的双转子结构设计方案。但由于中介轴承的存在，高低压转子的动力特性可能相互影响，导致双转子系统振动变得更为复杂，给发动机结构系统设计和振动故障诊断带来困难和挑战。

为研究带中介轴承的双转子系统动力特性，1980年，Hibner[1]用传递矩阵法计算分析了具有黏性阻尼双转子系统的临界转速及不平衡响应。20世纪90年代，Gupta等[2-3]研究并分析了轮盘的转动惯量和陀螺效应对双转子动力特性的影响。此后，Guskov[4]、罗贵火[5-7]等、采用传递矩阵法研究并验证了双转子系统的典型振动特性以及支承刚度、陀螺效应对双转子振动特性的影响。洪杰[8-9]、张大义[10-11]和左彦飞[12-14]等针对发动机的双转子系统，主要使用有限元模型研究了临界转速、稳态不平衡响应的计算分析方法，对典型发动机的双转子系统动力特性进行了分析，得到了系统响应特征，并研究了支承非对称等因素的影响。在双转子系统线性动力特性研究的基础上，近年来学者对非线性因素影响下的双转子系统响应也做了较为深入研究[15-20]。不过，现有的研究主要集中于双转子-中介轴承系统建模，临界转速、不平衡响应的计算分析，以及考虑中介轴承非线性的动力学特性分析等。主要通过计算出的响应结果、轴心轨迹或试验的现象，研究双转子系统振动特征。双转子系统因中介轴承而存在振动耦合作用的机理以及如何进行评估耦合的强弱等问题，在双转子系统设计或振动故障分析中具有重要意义，还需要深入研究。

为此，通过单转子和耦合双转子系统的振型相似性变化、临界转速变化、中介轴承受力变化、工作转速内系统应变能分布变化分析等，提出双转子系统振动耦合作用机理及影响评估方法，以某典型带有中介轴承的发动机双转子系统为对象，分析了该双转子系统通过中介轴承的耦合作用，为类似的发动机转子系统动力设计及故障诊断提供参考。

1 耦合作用评估方法

1.1 转子系统动力学方程

基于有限元建模的单转子系统动力学方程可表示为

(1)

式中：Mi、Ci、Gi、Ki、Ωi、fi分别为单转子系统的质量矩阵、阻尼矩阵、陀螺矩阵、刚度矩阵、转速、激励向量；ui为单转子系统振动位移向量；t为时间；j为虚数。

带有中介轴承的双转子系统的动力学方程可表示为[12]

(2)

式中：M、C、Kd分别为双转子系统质量矩阵、阻尼矩阵、刚度矩阵；Ω1、G1、K1、f1和Ω2、G2、K2、f2分别为低压转子(转子1)和高压转子(转子2)的转速、旋转产生的陀螺效应矩阵、转速相关的刚度矩阵、激励向量；u为双转子系统振动位移向量。

对于连接双转子的中介轴承，若忽略其质量、阻尼、非线性因素，刚度矩阵用kb表示，设中介轴承与低压转子、高压转子相连接节点编号分别为l、h，则中介轴承与低、高压转子耦合的力学方程可表示为[13]

(3)

比较式(1)～式(3)可以看出，相对于单转子系统，中介轴承的连接作用的影响主要有两方面：一是系统刚度的明显变化，会使系统的固有特性发生变化；二是传递复杂不平衡激励到另一个转子，会使得系统的响应特性发生变化。因此，对中介轴承耦合作用机理及影响的评估将主要从转子的振型、临界转速等固有特性以及不平衡响应特性两个方面开展。

1.2 中介轴承耦合作用对振型与临界转速的影响

利用复模态求解方法，可由式(1)得到单转子系统的临界转速对应的模态振型矢量Ψs(Ωcn)，其中Ωcn表示单个转子的第n阶临界转速。

而对于特定的双转子系统，两个转子的转速关系往往是确定的。假设两个转子的转速关系符合：

Ω2=f(Ω1)

(4)

并利用文献[10]所述的双转子系统临界复模态求解方法，可由式(2)得到被耦合转子激励的临界转速对应的模态振型矢量Ψd(Ωcm)，其中Ωcm表示双转子系统的第m阶临界转速。

1.2.1 振型及临界转速变化评估

为研究中介轴承及另一个转子的存在对原单一转子系统振型(频率)产生的影响，利用振型相似性指标-振型置信因子(量符号记为Cma)来定量评估振型的受影响程度。理论上转子振型受转速影响，模态置信因子是两个转子转速的函数。不过，由于工程中比较关注临界转速对应的转子振型，所以提出临界转速对应的模态振型置信因子，其表达式为

(5)

式中：Cmamn为同一转子耦合前的第n阶临界转速与耦合后的第m阶临界转速的振型置信因子；n表示单个转子(低压或高压转子)在转速范围内临界转速的阶次；m表示该转子激励的双转子在转速范围内临界转速的阶次。

通过计算振型置信因子，得到不同阶模态振型的相似性。当Cmamn为1.00时，两个振型完全相同，越接近于1.00相似性越大，Cmamn最小为0[21]。通过Cmamn的大小，并结合对应的振型，评估单转子耦合前后在临界转速位置的振型受影响程度。

进一步研究转子耦合前后Cmamn较大的两组振型Ψs(Ωcp)、Ψd(Ωcq)对应的临界转速的相对变化率，可以表示为

(6)

1.2.2 振型应变能变化评估

在发动机转子系统设计中，可根据应变能分布准确判定系统振型中转子与机匣振动主次，如果转子部件的弯曲应变能过高，则要通过设置阻尼器、柔性转子高速动平衡等措施调整应变能分布，因而具有重要作用。在双转子-支承系统中，由于转子通过中介轴承与另一转子耦合，应变能的分布变化在系统设计与故障诊断应重点关注。为了定量分析单一转子系统耦合前后临界转速对应振型的应变能变化情况，提出模态应变能占比变化量指标。

若Ee1、Er1、Ep1、Ea1和Ee2、Er2、Ep2、Ea2分别表示单转子耦合前后在临界转速时的单元应变能、转子应变能、单个支承应变能、所有支承单元应变能。则单元、转子、单个支承、所有支承的相似模态振型在耦合前后的模态应变能占比变化量可表示为

(7)

式中：*可表示e、r、p、a。

1.3 中介轴承耦合作用对不平衡响应的影响

由于转子系统的固有特性受转速的影响，且在设计或故障诊断时常常需要考虑在0～110%工作转速范围内响应特性。求解得到式(2)所述的双转子动力学方程中低、高压转子分别激励下转子系统的响应：

(8)

式中：

由于中介轴承为连接两个转子的关键承力部件，双转子不平衡振动相互耦合作用主要由中介轴承传递，全转速范围内中介轴承受力变化可以从相互作用力的角度表征双转子间的耦合程度，同时可为中介轴承设计及故障诊断等提供参考，中介轴承受力表示为

fb=Δu·kb

(9)

在此基础上，进一步评估在中介轴承耦合作用下，从单转子系统到双转子系统，全转速范围内的不平衡振动能量分布变化情况。分别计算特定不平衡激励下单转子及双转子系统在每个转速下的单元应变能、转子应变能、支承系统应变能，则利用式(7)可以计算得到转子系统应变能占比变化量，进而可以评估整个转速范围内转子受耦合的影响程度。

2 典型带中介轴承的双转子系统耦合动力特性分析

以文献[14]所述的同向旋转双转子系统为对象，结合所提评估方法，研究中介轴承的耦合作用对双转子动力特性的影响规律。

2.1 典型发动机双转子支承系统

如图1所示，该双转子系统共有6个支点(轴承)位置，其中1号、2号、3号与6号支点为低压转子支点，4号支点位置为高压转子支点，5号支点为中介支点，低压压气机与低压涡轮通过低压涡轮轴连接组成低压转子。转子的轴向为X方向，与X方向垂直的平面内相互垂直的两个方向分别为Y、Z方向。双转子的主要部件参数见表1[14]， 双转子系统的对称支承经验刚度见表2，低、高压转子分别计算时的经验刚度见表3、表4，其中单转子计算时高压转子5号支点的刚度通过低压转子5号支点位置的静刚度计算分析得到。参考该发动机双转子的实际工作转速变化规律，简化为文献[14]中图2所示的转速关系进行相关的动力特性分析。

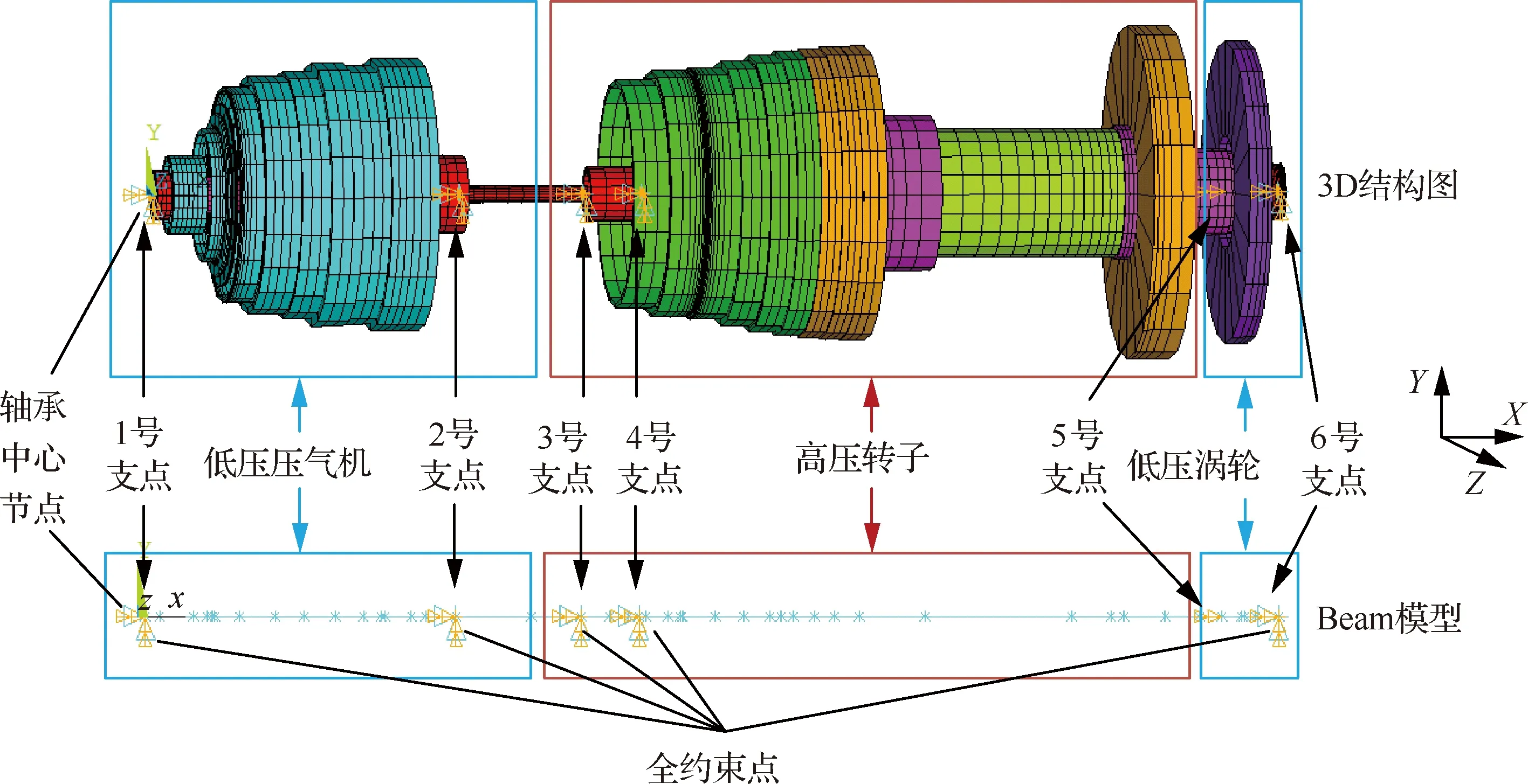
图1 典型双转子系统有限元模型

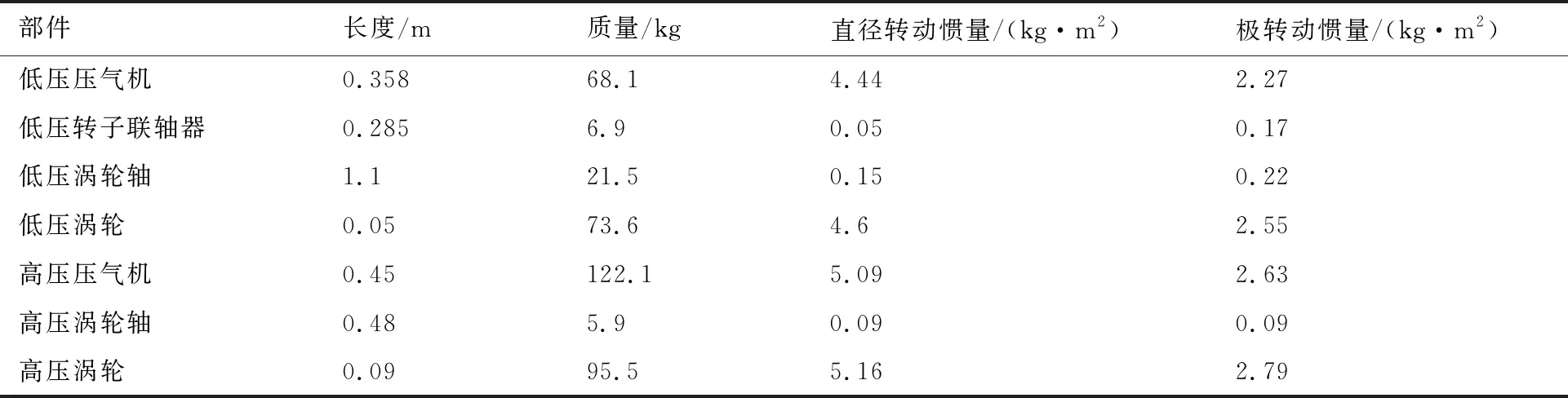
表1 双转子主要部件及参数[14]

表2 双转子系统的对称支承经验刚度

表3 低压转子系统的对称支承经验刚度

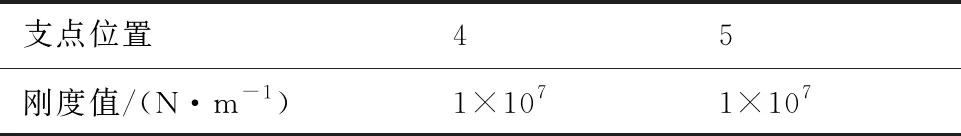
表4 高压转子系统的对称支承经验刚度

2.2 耦合作用对振型与临界转速的影响

根据1.2.1节所述的评估方法，研究并评估中介轴承耦合作用对振型与临界转速的影响。

通过分别对低压转子、高压转子以及双转子进行模态计算，并利用式(5)计算得到的单独低、高压转子与双转子耦合时的低、高压转子的振型置信因子分别如表5、表6所示，F表示正进动，B表示反进动，例如，1stF表示第1阶正进动临界转速，2ndB表示第2阶反进动临界转速。表中：加粗且带下划线的数字表示单独低压转子或高压转子与耦合双转子系统明显相似的振型置信因子；L、H分别表示单独低压、高压转子临界转速阶数，L-D、H-D分别表示低压、高压转子激励的双转子临界转速阶数。

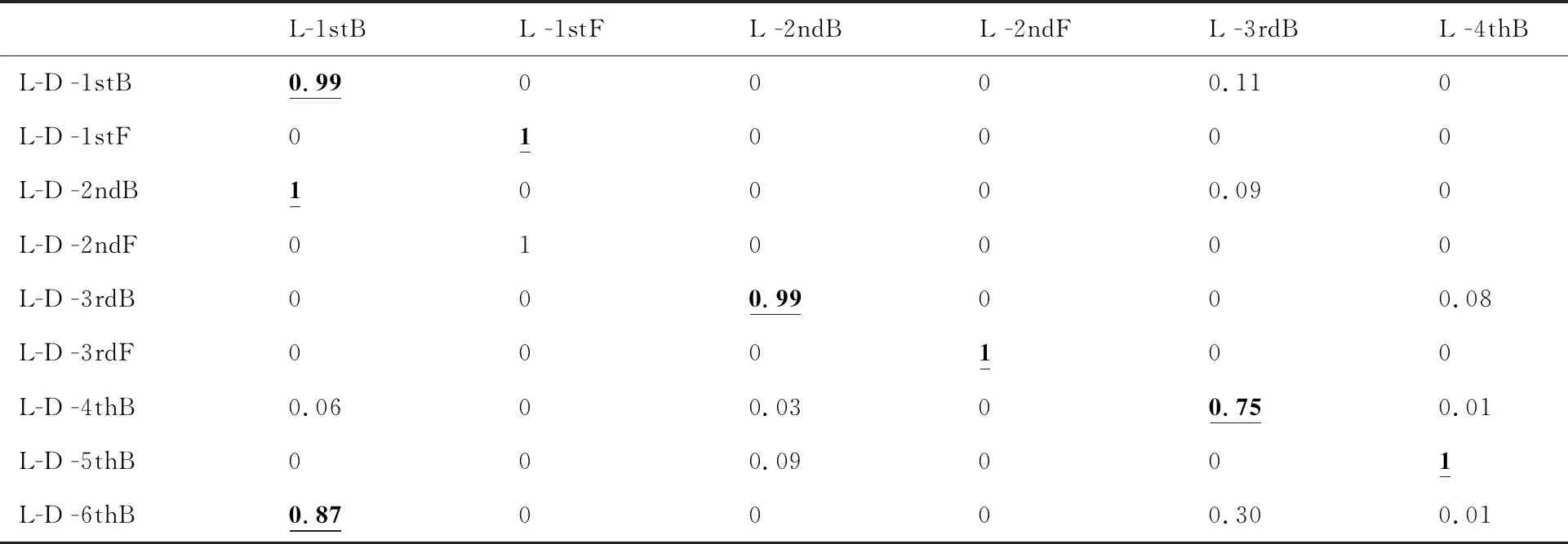
表5 低压转子激励与临界转速对应模态振型置信因子

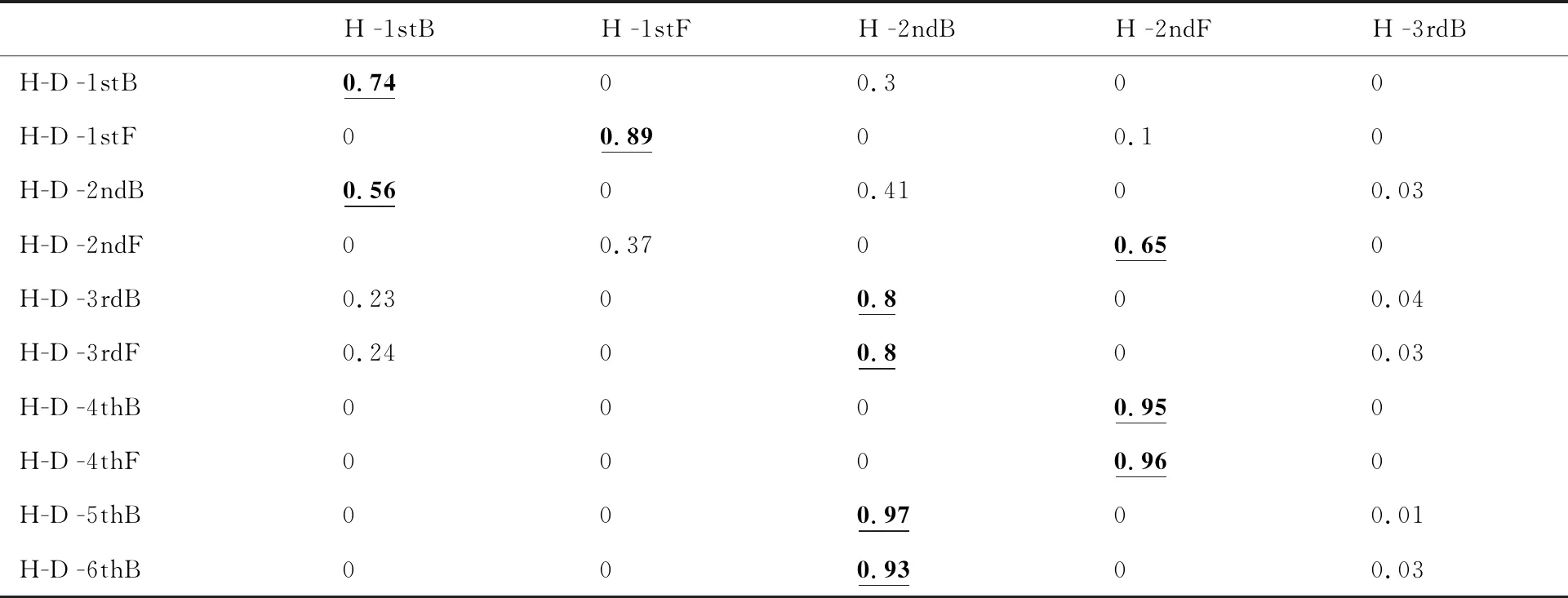
表6 高压转子激励与临界转速对应模态振型置信因子

由表5、表6可以看出，单转子的某些模态振型会在双转子高阶模态振型中出现，且为一对一的对应关系。例如单独低压转子的2ndB、2ndF和4thB振型分别与双转子中低压转子激励的3rdB、3rdF和5thB阶模态置信因子均在0.99以上，通过图2所示振型图，可以看出这几阶振型均以低压压气机的横向振动为主，低压涡轮和高压转子的振动较小，故振型相似度较高。进一步通过式(6)计算得到表7(其中L-D-C表示低压转子激励临界转速，L-C表示低压转子临界转速，下文相同)，可以看出与振型对应的临界转速相对变化率较小。

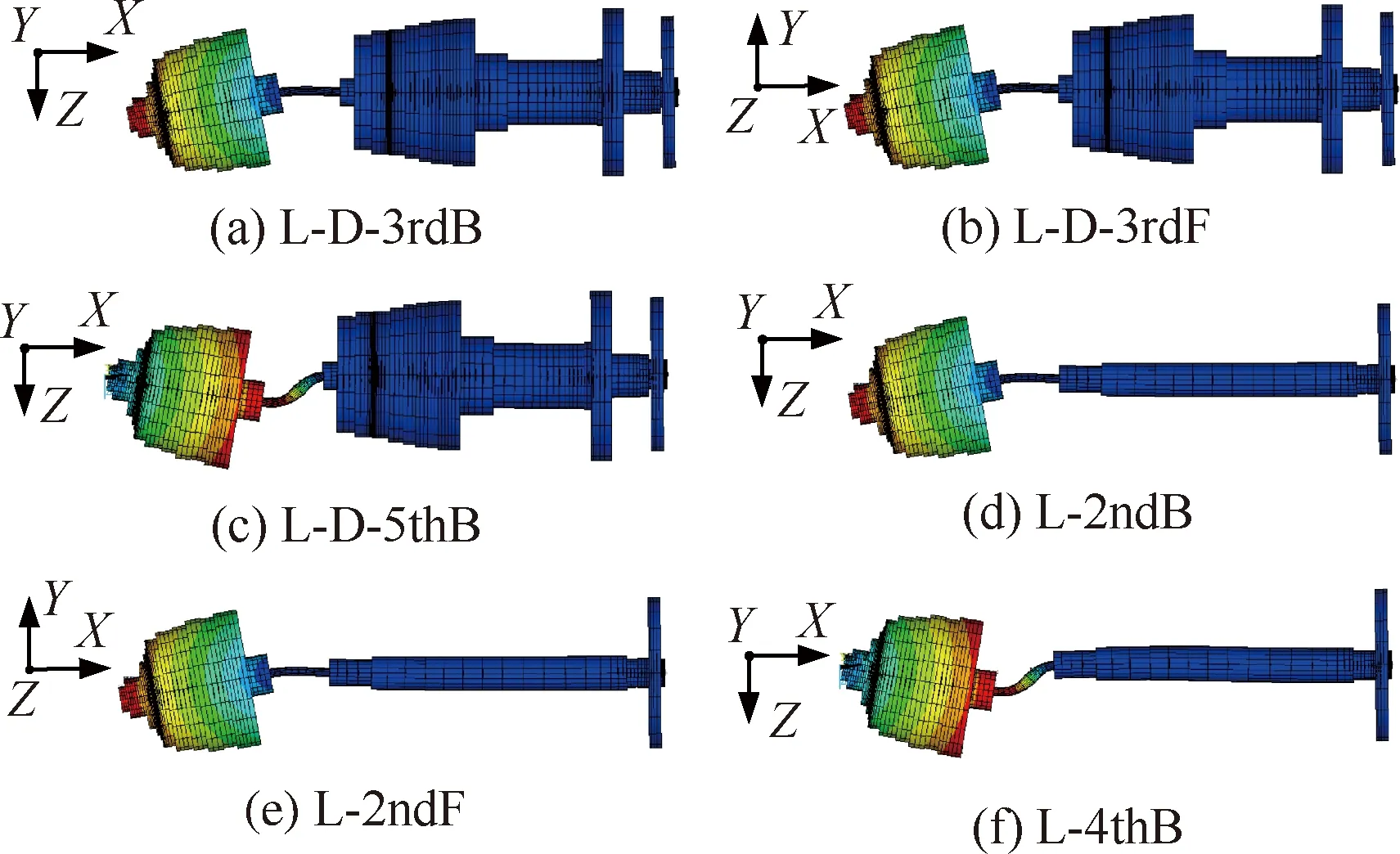
图2 双转子中低压转子激励的3rdB、3rdF、5thB和低压转子对应振型比较

表7 双转子中低压转子激励的3rdB、3rdF、5thB和低压转子对应临界转速比较

此外，单转子的特定模态振型可能在双转子模态振型中反复出现。例如单独低压转子1 stF与双转子中低压转子激励的1 stF与2ndF模态振型置信因子均为1，可以看出其振型(图3)也明显高度相似，均以低压涡轮和高压转子的俯仰振动为主，区别之处在于高压转子振型不同。但由表8可以看出与振型对应的临界转速相对变化率可能较大。

表8 双转子中低压转子激励的1stF、2ndF和低压转子对应临界转速比较

特殊的，由表6可以看出，双转子中高压转子的某些模态振型是由单独高压转子的多阶不同占比的模态振型组成。例如双转子的1stB对应的单转子的1stB与2ndB的置信因子和约为1；双转子的2ndB对应的单转子的1stB、2ndB和3rdB的置信因子和约为1；双转子的2ndF对应的单转子的1stF和2ndF的振型因子和约为1，其中单独高压转子的各阶振型分别如图4(d)～4(h)所示。说明在这些临界转速位置，双转子系统的振型与单独转子系统相比发生明显的变化，此时，中

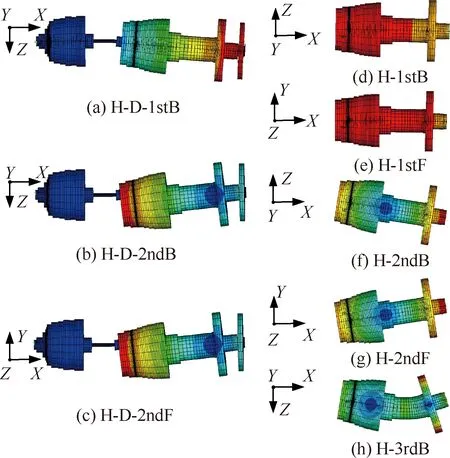
图4 双转子中高压转子激励的1stF、2ndB、2ndF和高压转子对应振型比较

介轴承的连接作用使得高压转子的支承特性发生显著变化，进而引起高压转子的两阶或多阶振型发生耦合形成新的振型。由对应临界转速的变化关系(表9，其中H-D-C表示高压转子激励临界转速，H-C表示高压转子临界转速)可以看出，振型相似性较高的振型对应临界转速变化可能较小，振型相似性较低的振型对应临界转速变化可能较大。

表9 双转子中高压转子激励的1stF、2ndB、2ndF和高压转子对应临界转速比较

在上述3种情况的振型相似性及临界转速变化分析的基础上，利用1.2.2节所述的振型应变能变化评估方法，进一步分析临界转速模态应变能的变化情况。

1) 对于单转子与双转子呈一一的对应振型且相似性较高的情况：双转子中低压转子激励的3rdB、3rdF和5thB振型对应的模态应变能如表10所示，可以看出，各部分应变能占比变化量最大不超过4%，此种情况下各阶临界转速对应转子、支点的应变能占比变化量均较小，结合振型分析可知这些临界转速均以低压压气机振动为主，中介轴承耦合作用甚微。

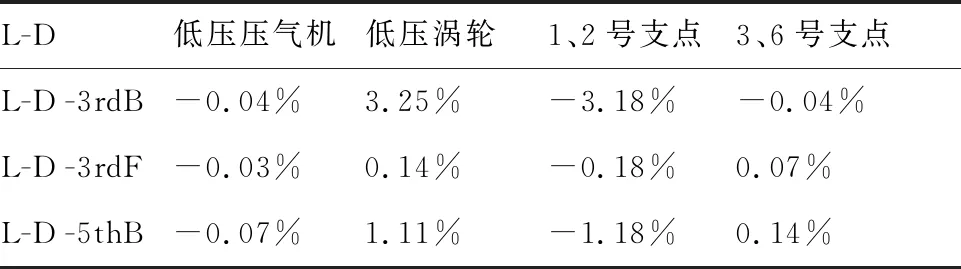
表10 低压转子激励的3rdB、3rdF和5thB临界转速对应的模态振型应变能占比变化量

2) 对于单转子的某阶模态振型在双转子模态振型中反复出现的情况：单独低压转子1stF与双转子中低压转子激励的1stF与2ndF振型对应的模态应变能如表11所示，可以看出，各部分应变能占比变化量最大不超过2%，此种情况下转子、支点对应的模态应变能占比也均较小，结合振型分析可知，这种情况下，高压转子的振型及其变化对低压转子影响很小。

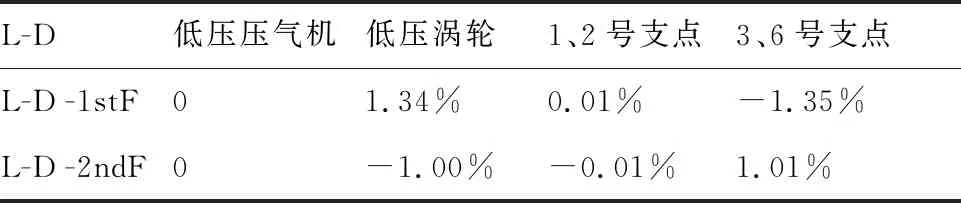
表11 低压转子激励的1stF、2ndF临界转速对应模态振型应变能占比变化量

3) 对于双转子中高压转子的单阶模态振型是由单独高压转子的多阶不同占比的模态振型组

成的情况，双转子中高压转子激励的1stB、2ndB和2ndF振型与单独高压转子对应振型的模态应变能占比变化量如表12所示。可以看出，振型置信因子较小的应变能占比变化量较大，如双转子中高压转子激励的2ndB与单独高压转子3rdB的置信因子为0.03，高压转子应变能占比变化量达到了-98.26%；但是对于模态振型置信因子越大对应的应变能占比变化量却不一定小。

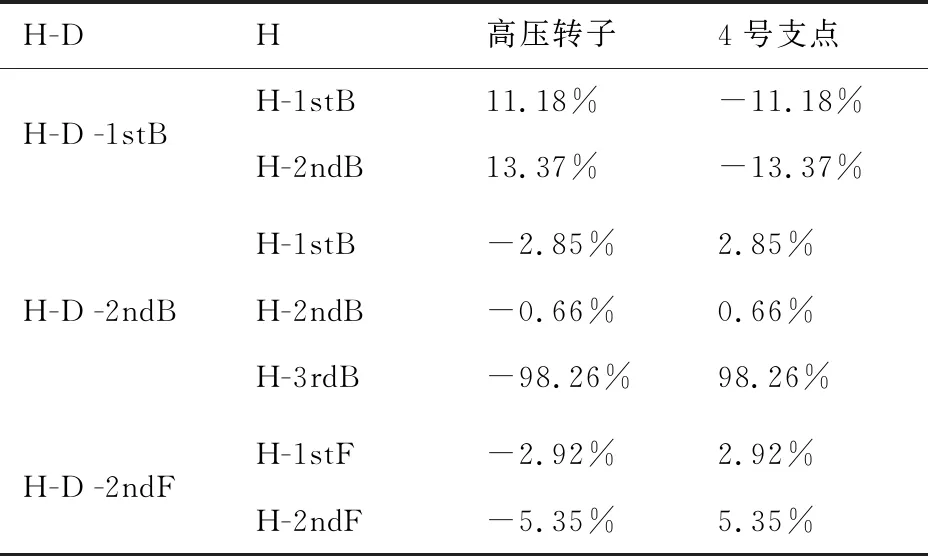
表12 高压转子激励的1stB、2ndB和2ndF临界转速对应模态振型应变能占比变化量

2.3 耦合作用对稳态不平衡响应的影响

利用1.3节的评估方法，研究中介轴承耦合作用对不平衡响应的影响。

当低压涡轮叶盘、高压涡轮叶盘上分别施加2 g·m允许不平衡量时，求解得到的双转子系统各支点的响应分别如图5、图6所示。转子各支点临界转速位置响应的相对大小与振型相关及激励位置相关，这与文献[12]的结论一致。

进一步分析中介轴承弹簧单元在低压转子、高压转子受耦合时力的传递关系，分别绘制低压、高压转子激励时5号支点节点力随转速的变化规律如图7、图8所示，结合图5、图6可知，中介轴承节点力与位移响应曲线在转速范围内的变化一致，在临界转速位置同时到达峰值，且高、低压转子5号支点节点力随转速变化曲线相同。

图5 低压转子激励时双转子各支点的响应

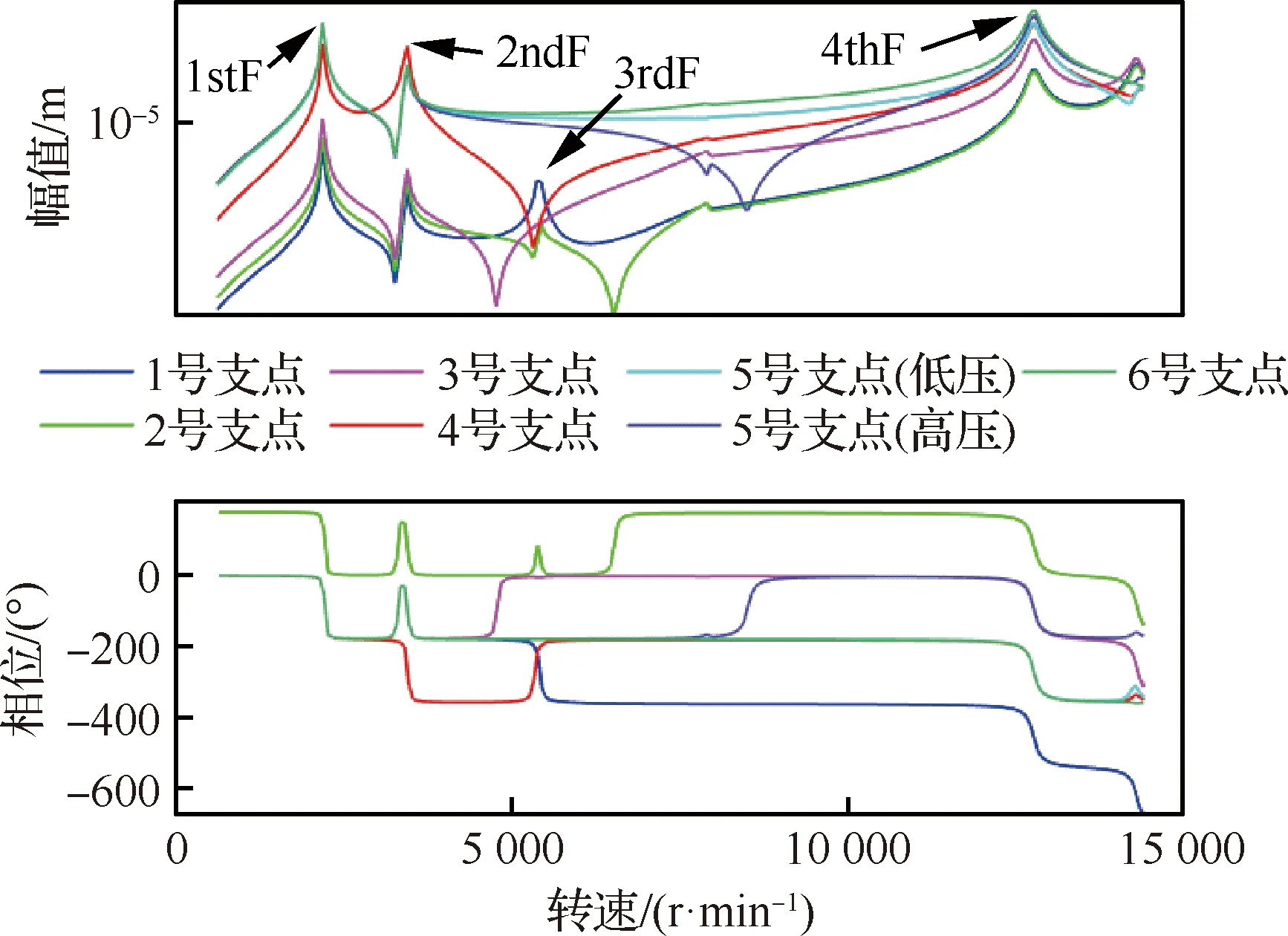
图6 高压转子激励时双转子各支点的响应

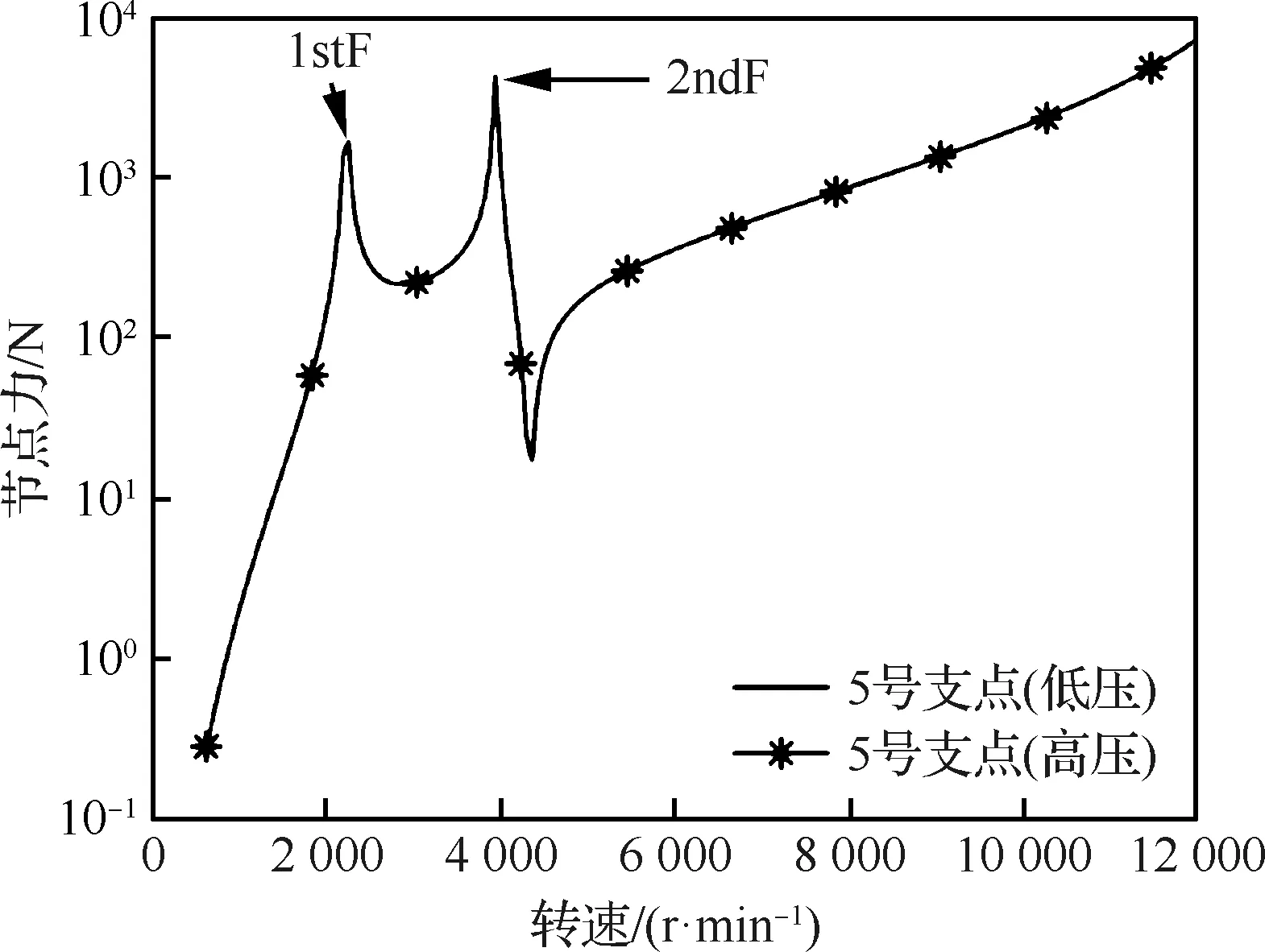
图7 低压涡轮存在不平衡激励时5号支点节点力

图8 高压涡轮存在不平衡激励时5号支点节点力

为了分析双转子中低压转子(高压转子)激励时受高压转子(低压转子)耦合作用的影响程度，通过计算低压转子(高压转子)单转子有相同不平衡量时的不平衡响应，并绘制在整个转速范围内的低压转子(高压转子)-支点应变能占比变化量如图9、图10所示。

可以看出，双转子耦合作用较强的位置不一定与转子响应较大的位置一致。例如，在图5中的位移响应峰值位置，转子-支点的应变能变化曲线(图9)并未达到峰值，如图9中低压转子支点在整个转速范围内的受耦合程度较大的位置为1stF与2ndF之间、3rdF之后；在图6中的位移响应峰值位置，图10中高压转子-支点在整个转速范围内的受耦合程度较大的位置为2ndF与3rdF之间。图9中除低压涡轮、6号支点应变能占比变化量较大外，其余部分在整个转速范围内变化均较小，几乎为0。

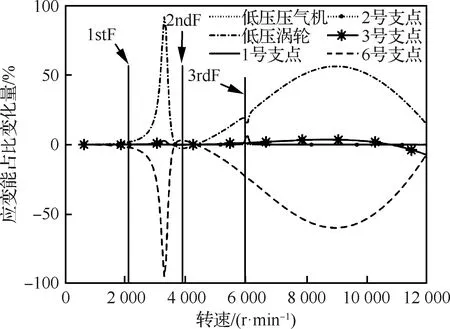
图9 低压涡轮激励时低压转子应变能占比变化量随转速变化曲线

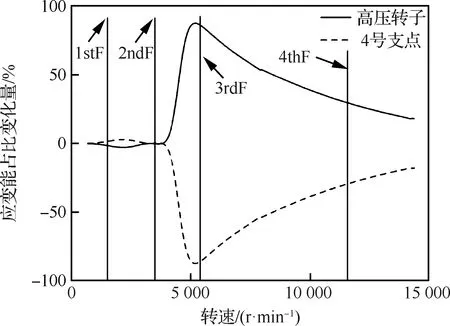
图10 高压涡轮激励时高压转子应变能占比变化量随转速变化曲线

而当低压压气机1级叶盘有相同不平衡量时，低压转子对应的应变能占比变化量如图11所示，转子、支点的变化量均很小，可以看出双转子系统的耦合作用对低压压气机不平衡量不敏感。从图2中的临界转速所对应的振型也能得到类似的定性结论。图11中除1号支点、6号支点应变能占比变化量相对较大外，其余部分在整个转速范围内变化接近于0。

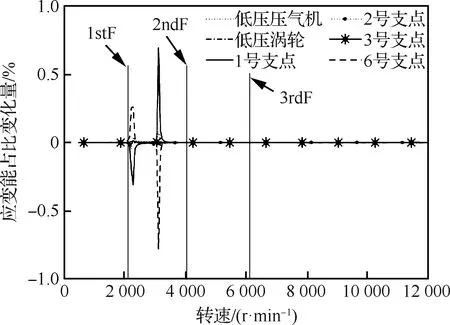
图11 低压压气机激励时低压转子应变能占比变化量随转速变化曲线

为了进一步分析在不同转速下转子不同位置的应变能变化，在图9、图10所示的转子各部分随转速变化的应变能占比变化量图的基础上增加第三维坐标-转子各单元位置，可以分别得到低压转子(或高压)激励时的低压(或高压)转子各单元应变能占比变化量随转速变化曲线如图12、图13所示。在某一转速下沿该图纵坐标方向看，为该转速下转子上各单元的应变能变化；若沿该图横坐标方向看，为特定单元的应变能变化随转速变化情况。

由图12、图13可知，在整个转速范围内，应变能变化较大的位置为5号支点所在的低压涡轮轴附近、高压涡轮及高压涡轮轴附近，说明这些位置受双转子耦合作用较大，在转子系统设计时应重点关注。此外双转子耦合作用较强的位置不一定在转子响应较大的位置，这与图9、图10的结论一致。

图12 低压转子激励时低压转子各单元应变能占比变化量随转速变化曲线

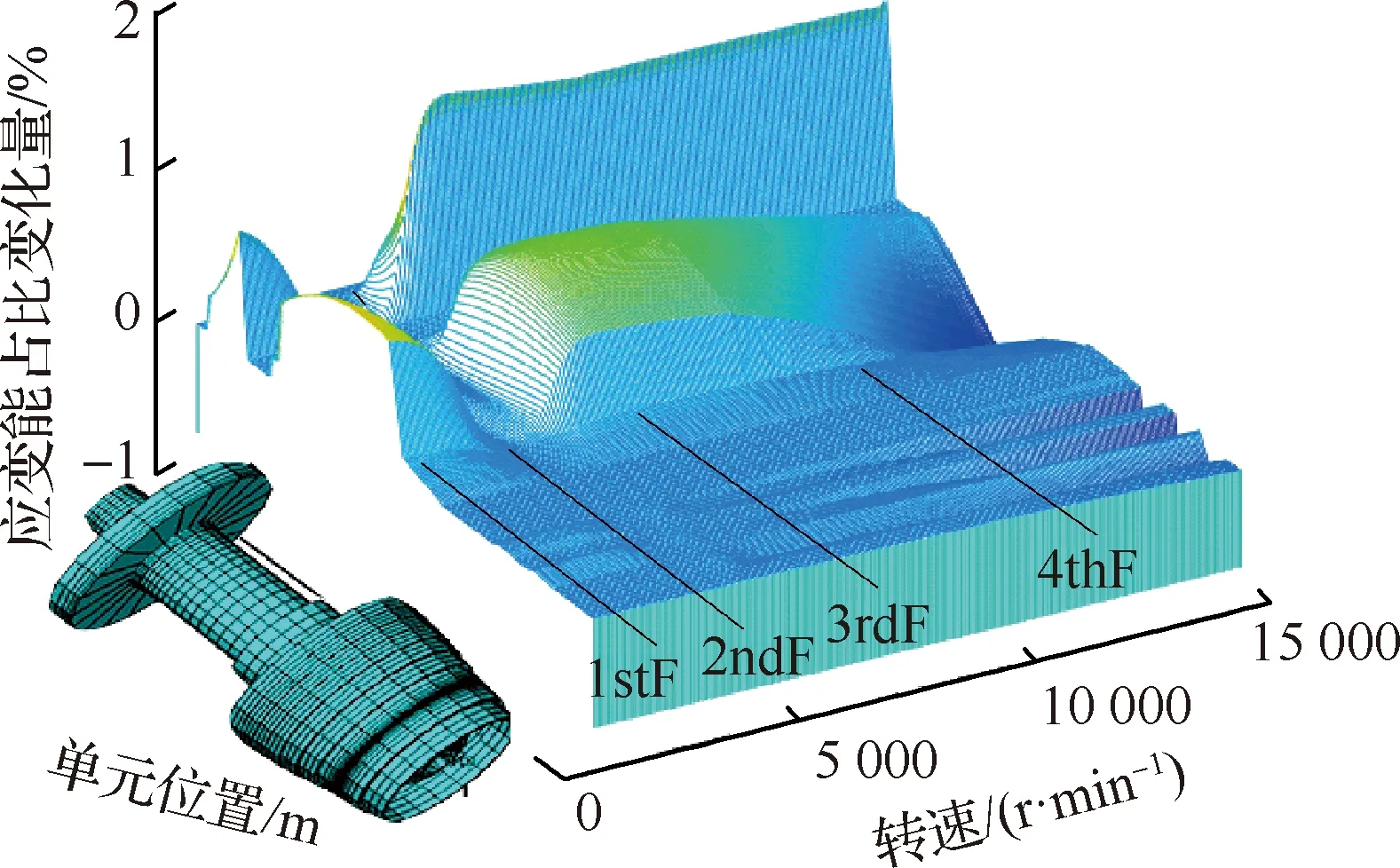
图13 高压转子激励时高压转子各单元应变能占比变化量随转速变化曲线

3 结 论

1) 双转子的耦合作用对振型及相应的临界转速影响主要有3种情况。一是由于中介轴承附近振动较小使得耦合作用较弱而几乎无影响，表现为单转子的部分模态振型会在双转子模态振型中出现，且为一一对应关系，振型相似性极高，临界转速相对变化率较小，应变能分布变化小；二是由于其一转子振型变化较大而另一转子改变较小导致振型重复出现，表现为单转子的一些模态振型会在双转子模态振型中重复出现，且振型相似性较高，临界转速相对变化率可能较大，应变能分布变化较小；三是由于其一转子振型变化较大导致另一转子支承特性改变而出现耦合振型，特别是高压转子，表现为双转子中单阶模态振型与单独转子的两阶或多阶模态振型有一定相似性，且与这些模态振型的置信因子之和接近1，此时，对应的临界转速以及应变能分布变化较为复杂，需具体分析。

2) 通过全转速范围内的稳态不平衡响应分析发现，中介轴承在临界转速位置受力最大，而应变能分布变化最大的转速位置与系统临界转速位置不一致。同时受不平衡激励位置影响，耦合作用对涡轮位置的不平衡量更为敏感。进一步通过全转速范围内各单元应变能占比变化量随转速变化曲线可以详细分析特定不平衡激励下应变能分布变化情况，为转子系统设计或振动分析提供参考。