基于深度学习驱动的L型定向热疏导机理
2021-07-07王泽林籍日添惠心雨丁晨汪辉白俊强
王泽林,籍日添,惠心雨,丁晨,汪辉,*,白俊强
1. 西北工业大学 航空学院,西安 710072
2. 中国运载火箭技术研究院,北京 100076
碳/碳(C/C)复合材料是以碳纤维或石墨纤维为增强体的碳基复合材料,其全质的碳结构不仅保留了纤维增强材料优异的力学性能和灵活的结构可设计性,还兼具碳素材料低密度、低热膨胀系数、优异的耐热冲击、耐摩擦及耐烧蚀等优点[1]。尤为重要的是,该材料的强度随温度升高不降反升,使其成为航空航天等领域理想的结构材料[2-4]。虽然C/C复合材料是一种优异的轻质耐高温热防护材料,但是现有C/C复合材料受限于其自身不高的传热性能,无法对飞行器表面热流进行有效热疏导,致使局部温度过高,材料结构发生变化进而加速失效,无法满足未来超音速飞行器热防护要求。而且常规的C/C复合材料在400 ℃以上会迅速氧化,从而导致各种性能的明显劣化;当温度达到1 800 ℃以上时,复合材料会因剧烈热冲击、高热流密度、强气流冲刷等服役条件变化导致表面发生烧蚀,这种氧化性烧蚀严重制约了C/C复合材料在严酷环境下的应用[5],也限制了其应用范围,因此本文提出了在C/C复合结构中内置L型的高导热碳纤维丝对飞行器表面受热严重区域的热量实施定向疏导,以期对其表面剧烈的氧化烧蚀做出有效防护的方法。
有效导热系数作为热防护材料重要的热物理性质,对其精确的评估是不可避免的,目前常使用有效介质理论(EMT)[6-8]直接求解热扩散方程[9],通过求解玻尔兹曼输运方程(BTE)[10]等方法预测复合材料的有效导热系数。EMT[11]提供了简单的分析模型,它可以快速地估算出复合材料和多孔介质的有效导热系数[12],这种方法虽然简便,但是由于没有考虑结构内部物质分布的影响,因此准确率受到了限制。为考虑材料内部的物质分布,直接求解热扩散方程的方法逐渐得到了应用。为求解热扩散方程,许多数值方法被提出,例如有限容积法[13]和有限元素法(FEM)[9]。格子-玻尔兹曼方法(LBM)[14-15]通过在介观尺度下求解BTE[8,16]计算有效导热系数。所有这些方法都是基于各种物理模型通过迭代求解方程得到有效导热系数的,这通常需要花费大量的时间和计算资源,且方法的精确度往往以牺牲时间和计算资源为代价,这不仅为工程上的实际应用和庞大模型计算带来了阻碍,更不利于对介观结构的热疏导性能进行搜索优化[17]。另一方面,实验方法也通常被用来研究复合材料的热传递[18],但这会产生实验成本高和测量不确定性高等问题。
随着机器学习方法的迅速发展,近年来,人们越来越对开发替代模型解决基于数据分析的工程问题感兴趣,在航空领域方面也不例外[19-20],这种方式可以绕过对物理机理的详细理解和实验测量从而大幅提高预测效率,在结构有效导热预测方面也是如此。例如,Wei等[21]利用二维卷积神经网络(2D-CNN)通过2D灰度图像很好地预测了二相孔隙结构的有效导热系数,相比之下,三维卷积神经网络(3D-CNN)在理论上可以直接提取三维结构的三维特征图像,已被证明可以建立高精度的结构-性能连接;然而,在复合材料中获得3D微观结构在现实中具有挑战性,因此Rong等[22]通过对3D多孔结构的多个2D横截面图像分别采用2D-CNN,从而预测了3D多孔材料的有效导热系数,但是正如其论文所证实的,使用这种方法时截取的2D图片的位置和数量均会直接影响预测的准确度。对于采用3D-CNN直接预测三维三相复合材料有效导热系数方面还鲜有报道。
本文将数值模拟方法的离散模型直接作为3D-CNN的三维结构样本,通过使用格子模型的方法将微观结构进行简化从而解决在复合材料中难以直接捕捉3D微观结构的问题,这不仅能建立一种直接从三维定向热疏C/C复合结构映射到有效导热系数的有监督CNN方法,还能大幅提高3D-CNN预测三维结构有效导热系数的精确度。在本文所属的3D-CNN模型中,内置的3D卷积核可从输入的三维结构中自动捕获结构的潜在特征,并将隐藏的微观结构信息汇总到其最终的预测之中,在其得到训练后,可以快速预测含有不同纤维丝半径、随机孔隙率和孔隙分布的定向热疏结构的有效导热系数,采用验证集验证CNN模型的高准确性,并通过测试集分别做出以下研究分析:① 研究定向热疏复合结构中L型纤维丝横向和纵向部分的半径对其纵向热导率的影响,以期通过改变L型纤维不同部分半径验证L型纤维丝的定向热疏特性;② 研究当测试集样本结构孔隙的分布、各向同(异)性程度和孔隙率超出训练集时CNN模型的预测表现,分析随机孔隙结构在CNN预测过程中的作用情况。
1 物理和数学模型
1.1 3D定向热疏介观结构生成
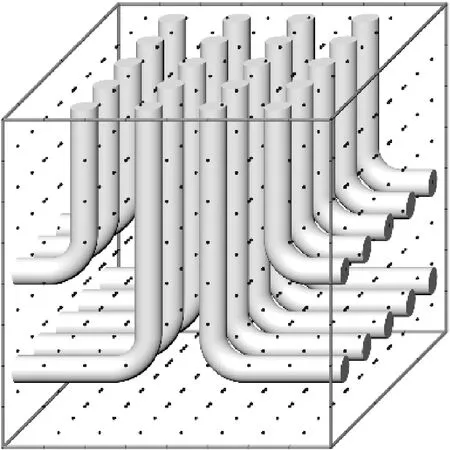
基于中间相沥青基碳纤维(MPCF)的导热系数可高达900~1 000 W/(m·K),如图1,将MPCF-K1100[23]制成L型纤维丝形状,以期将受热面(图1中顶面)的热量高效快速疏导至低温区域,计算域的大小以格子(lu)为单位,为100 lu×100 lu×100 lu,如图1所示,纵向及圆弧纤维丝半径为r1,横向纤维丝半径为r2。
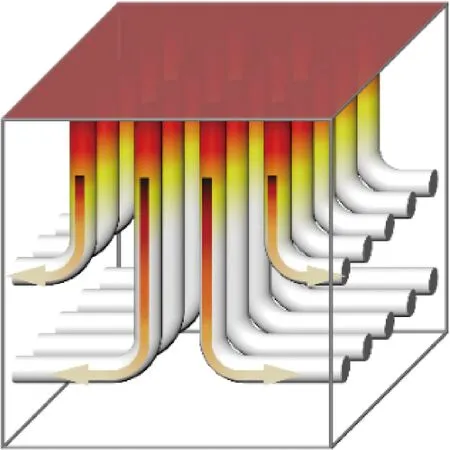
图1 定向热疏结构疏导高温区域热量
四参数随机生长法(QSGS)是一种可用于生成随机多孔介质的方法,通过4个参数控制多孔介质的内部多孔结构。QSGS可生成类似于实际多孔介质成形过程的多孔特征,在这4个参数中,岩心分布概率cd、生长阶段的体积分数p和定向生长概率Di可以分别确定孔径、孔隙率(ε=1-p)和孔隙分布,方向生长概率Di(下标i表示方向)确定孔隙分布是各向同性还是各向异性,采用QSGS布置三维定向热疏C/C复合结构中的基体孔隙结构。
综上所述,三维定向热疏结构生成具体流程的二维截面示意图如图2所示,即首先分别在L型纤维丝的中心位置布置好纤维丝的核心线,然后基于r1和r2沿径向生长指定半径的L型纤维丝,最后基于QSGS生成基体碳和孔隙结构 (此处孔隙只分布在基体碳里面,不会分布在高导热碳纤维丝中)。
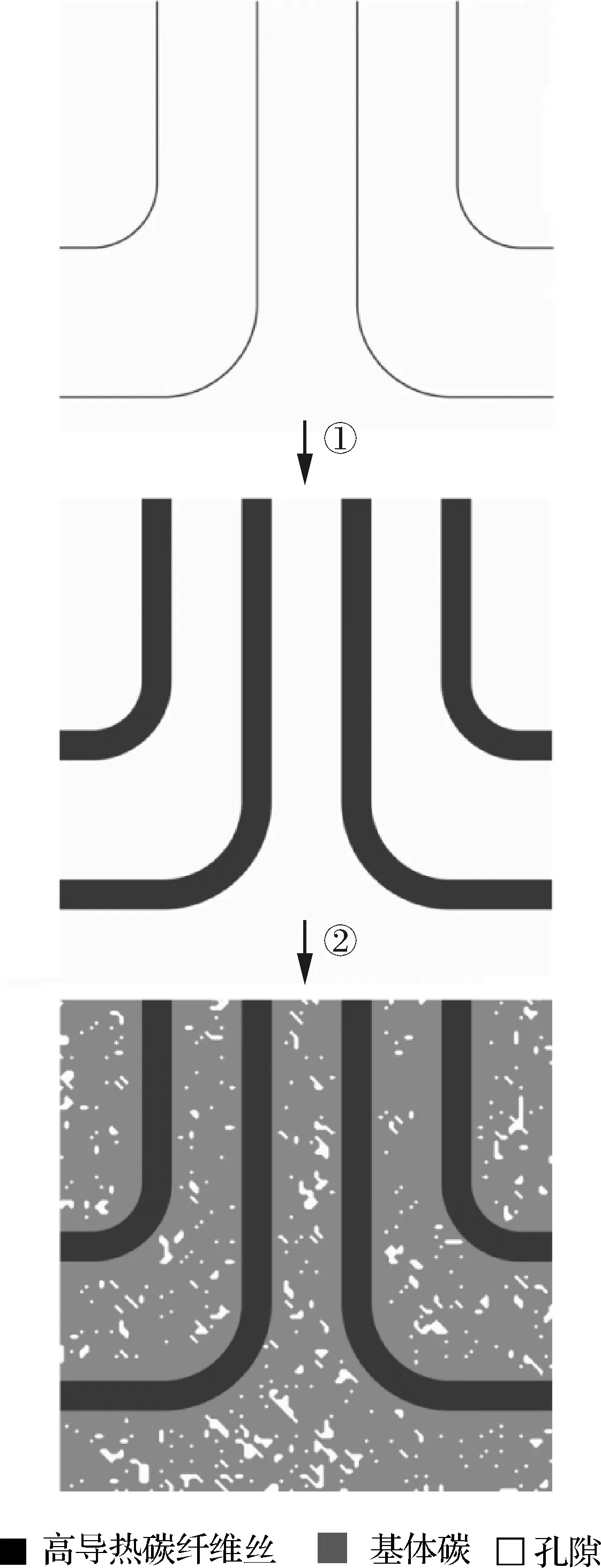
图2 定向热疏结构生成的二维示意图
1.2 有效导热系数数值计算
采用格子玻尔兹曼法基于对温度模型的离散,利用分布函数求解温度场,并以温度场求解结构内部的热流及介观结构的有效导热系数。LBM对于不同模型的控制方程均可以写作
(1)
式中:fi为分布函数,表示格子节点r=r(x,y,z)处的粒子数并且在时间t、方向i上的速度ei通过距离Δr=eiΔt连接最近的相邻格子,其中Δt为传播到相邻格点的时间;b为格子中信息传播的方向数;Ωi为由粒子碰撞造成的fi变化。利用Bhatana-Gar-Gross-Krook(BGK)近似的单次弛豫法,离散的格子Boltzmann方程[24]为
fi(r+eiΔt,t+Δt)=
(2)
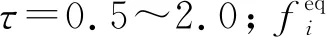
(3)
式中:α为扩散率,α=λ/(ρcp),其中λ为组分的导热系数,ρ为组分密度,cp为组分的比热。速度ei和相应的权重wi分别为
(4)
(5)
式中:C为系数。
在求解了模型中的温度场之后,对于n点处的温度Tn(r,t)和热流密度q在LBM中为[26-27]
(6)
(7)
式中:fn,i为n点处在方向i上的分布函数;ρn为n点处的组分密度;cpn为n点处组分的比热;wn,i为n点处权重;τn为n点处松弛时间。
当温度场以及热流得到求解之后,介观结构的有效导热系数keff根据定义可由式(8)确定:
(8)
式中:dA为介质截面积;L为距离;ΔT为温差。这些参数都由理论确定,keff的求解不存在经验因子。采用上述D3Q7模型计算内置高导热碳纤维丝的三相C/C复合结构,计算所需的物性参数如表1所示。
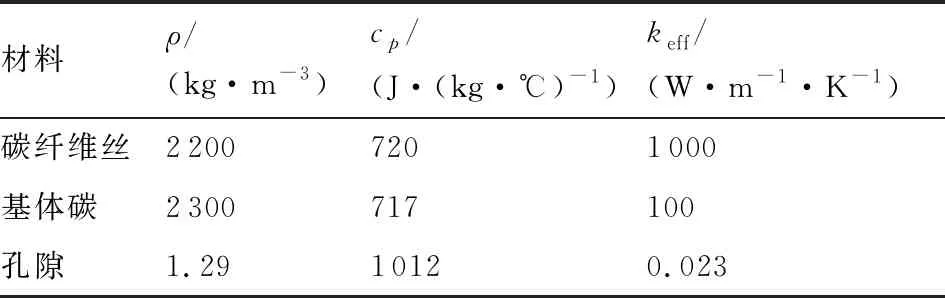
表1 C/C复合结构各组分的物性参数
1.3 边界条件处理
0≤x≤xmax,0≤y≤ymax,0≤z≤zmax,t≥0
(9)
式中:T(·)为温度函数;Tm为受热恒温面温度;T0为低温恒温面温度;xmax、ymax和zmax分别为坐标x、y和z的上限。
初始时,结构内部温度满足
T(x,y,z,t=0)=T0
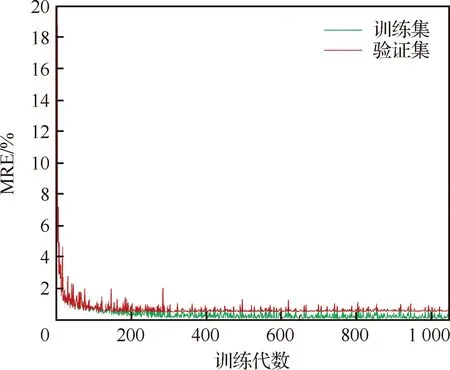
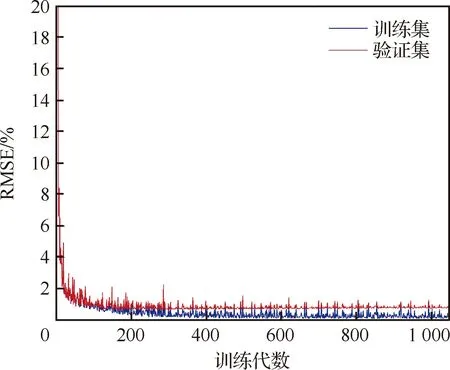
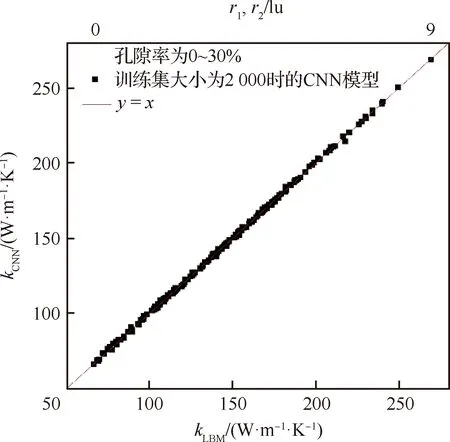
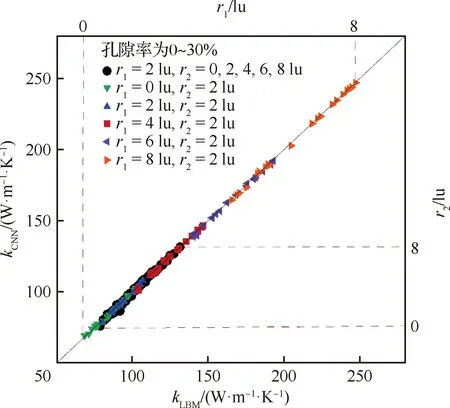
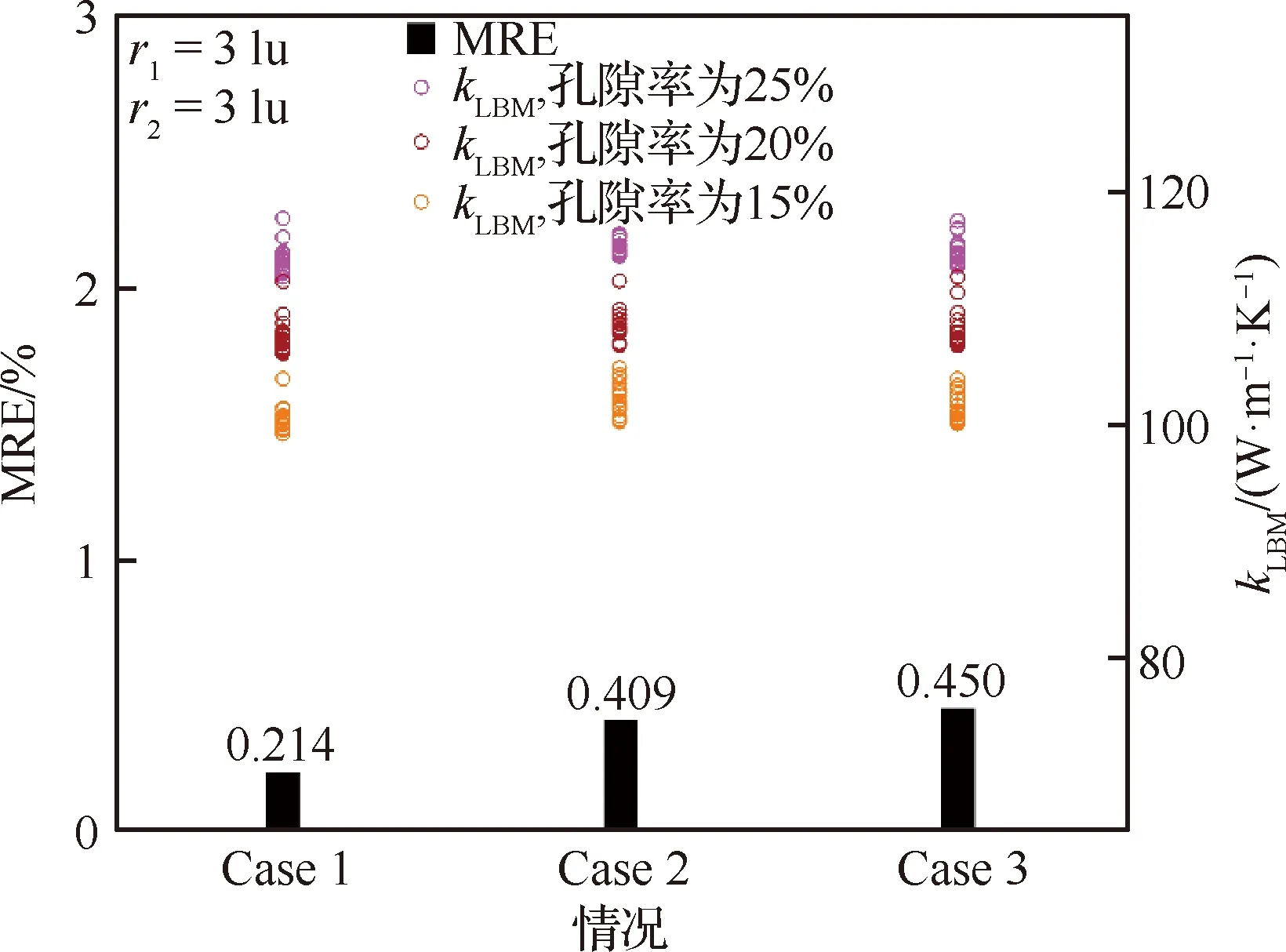
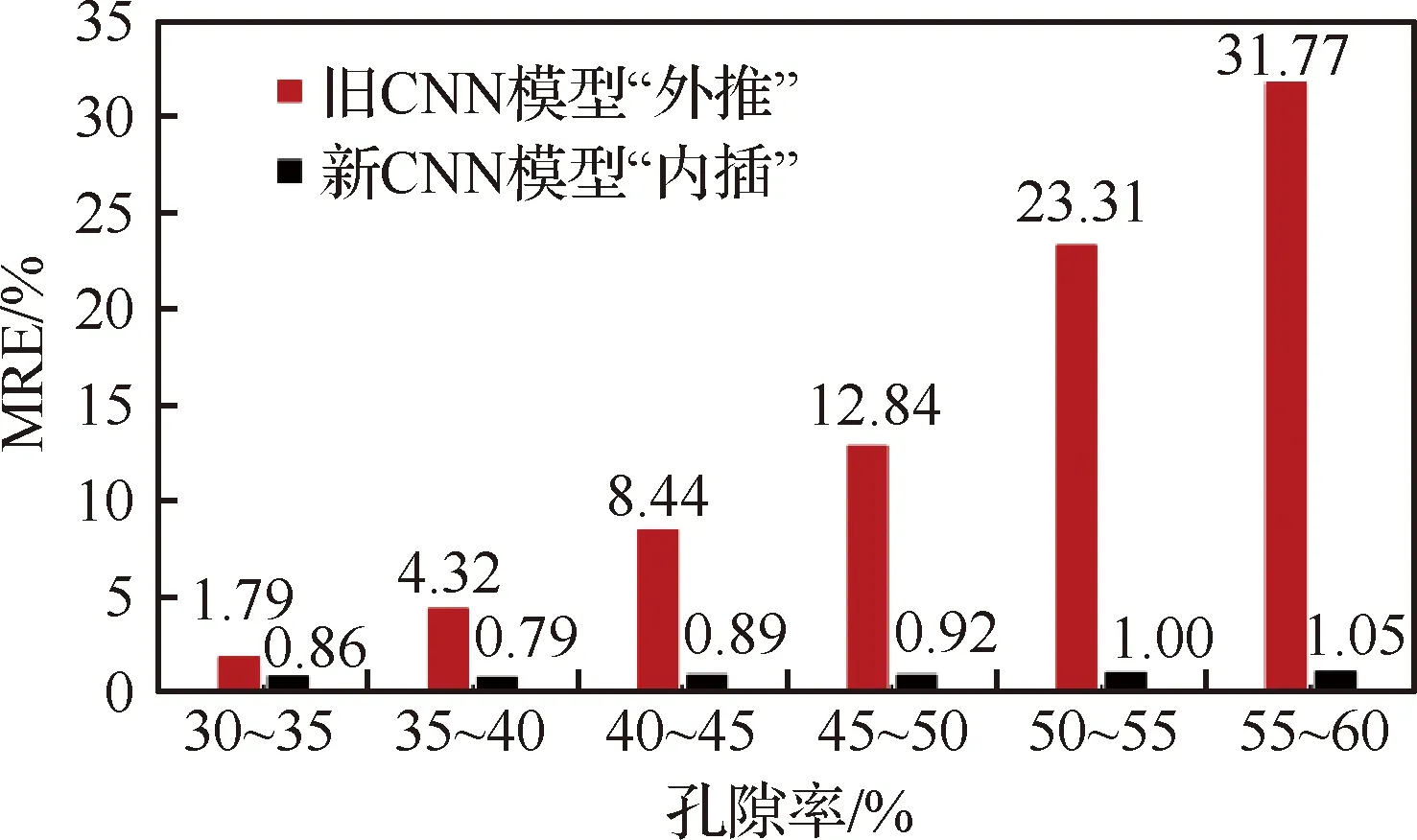
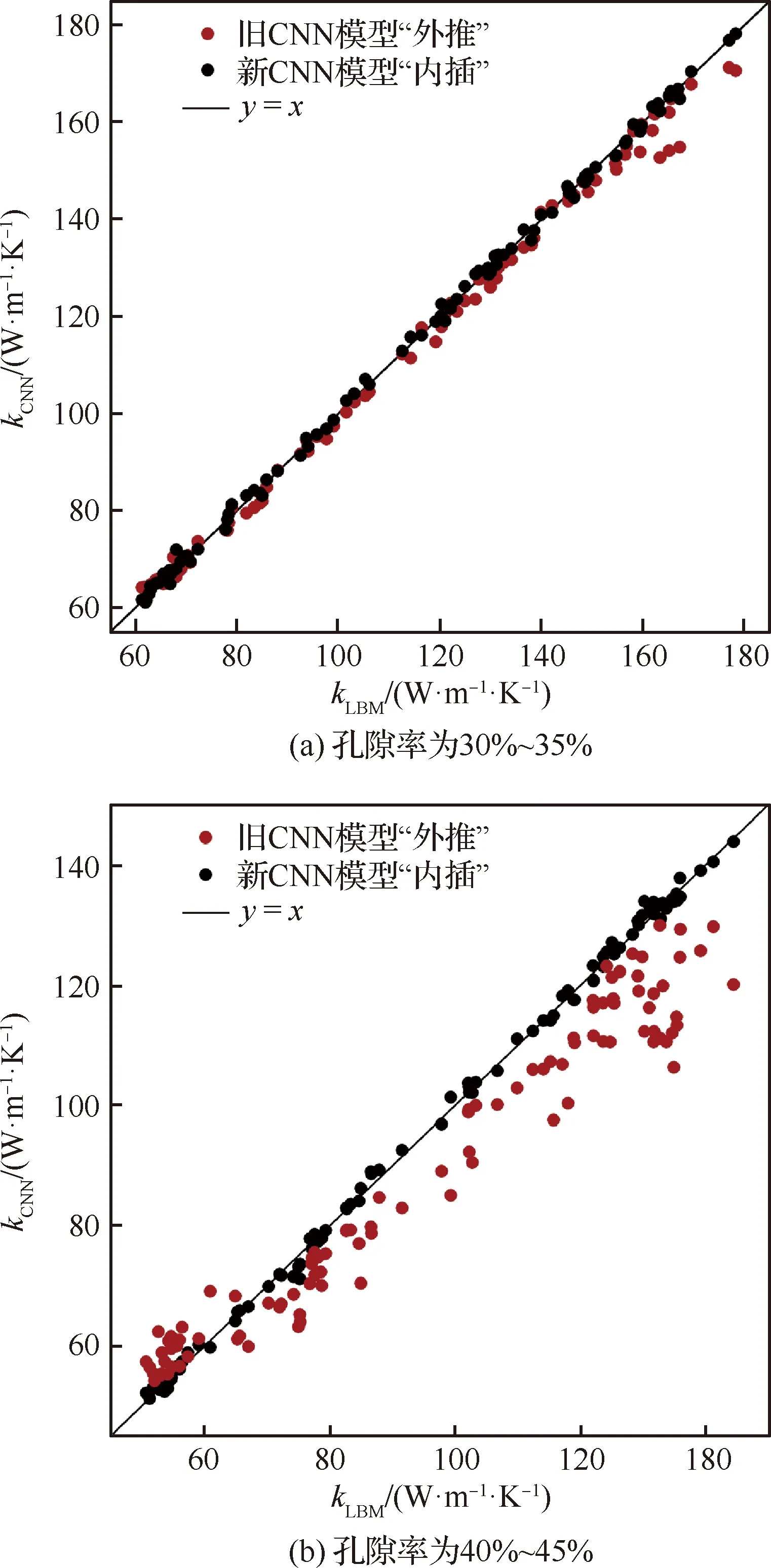
0 (10) 设Tm=100 ℃、T0=25 ℃,且对于温度T满足[26] 事务处理模块 事务处理模块主要包括用户事务和系统事务两部分,其中用户事务主要包括对用户信息的处理;而系统事务主要包括对播放器进行一些逻辑控制,如暂停、播放、截图等操作。 (11) (12) 通过式(11)和式(12)可得 (13) LBM法的边界条件在恒温边界(如图1顶面和底面)采用非平衡反弹格式[28]: (14) 在绝热边界(如图1前后左右4个侧面)采用反射格式[29]: fi=fj (15) 式中:下标i、j表征相反的方向,且恒温边界温度的平衡态分布函数可由其边界温度确定。 可以基于CNN所使用卷积核的维度将CNN的维度进行分类,Rong等[22]鉴于三维介观结构难以捕捉,因此通过二维卷积核提取3D多孔介质的多个2D横截面结构特征,从而预测了3D多孔介质的有效导热系数,但是由于所选择的2D样本图片无法完全反映原本3D介观结构的所有关键信息,换言之使用多个2D结构图片表征3D结构样本必然会损失原本3D结构的空间特征与信息,因此正如Rong等[22]所言,使用这种方法时截取的2D图片的位置和数量均会直接影响预测的准确度。采用带有三维卷积核的3D-CNN对具有L型纤维丝的定向热疏C/C复合结构的有效导热系数进行预测,3D-CNN模型的具体计算过程如图3所示,在计算过程中,可以将其分为3部分:数据读取、CNN计算和超参数的选择。 图3 3D-CNN的计算过程 采用的3D-CNN模型为典型的监督性学习方法,输入数据和输出,即标签一一对应。以3D定向热疏导结构的微观模型作为输入,并采用D3Q7的LBM模型计算了每个模型的有效导热系数作为标签,建立微观模型与有效热导率的映射关系。 为减少计算量和结构样本标签制作所耗费的时间并验证这种生成样本结构对同步简化数值模型和CNN模型的可行性,在使用LBM计算大小为100 lu×100 lu×100 lu介观结构的有效导热系数时将计算步长设定为2(经验证,该步长简化对热导率结果影响不大),即利用LBM格子模型中的偶数格子点计算介观结构的有效导热系数,因此原有的100 lu×100 lu×100 lu的介观结构计算出的有效导热系数将完全取决于LBM格子模型中的50×50×50个格子点,而3D-CNN样本数据的格式是张量(tensor)形式的,因此如图4示,将LBM中的50×50×50格子点对应数值的矩阵(如孔隙设为数字0,高导热碳纤维丝设为数字1,基体碳设为数字2,这些数字的具体取值并不影响结果,只是作为微观结构中不同材质的区分,图4列举了定向热疏介观结构的9×9×9的LBM格子模型以作形象说明)直接作为3D-CNN的三维输入样本张量。 图4 定向热疏导介观结构的9×9×9 LBM格子模型 机器学习方法需要训练数据生成模型,这些训练数据可以从任何可信赖的来源获取,包括数值模拟或实验。数据集由训练集、验证集和测试集3部分组成。训练集和验证集分别用于训练3D-CNN和检验训练后的CNN模型对有效导热系数预测的精确度,共生成了2 200个介观尺度下尺寸大小为100 lu×100 lu×100 lu的三维定向热疏结构,并将训练集和验证集按照10∶1的比例分配,在结构中L型纤维丝的r1、r2均采用变化范围为0~9 lu的随机数字(① 由于100 lu×100 lu×100 lu的格子模型模拟能力有限,因此无法模拟连续的半径变化,且格子数越多,模型所能模拟半径的变化越连续;② 由于纤维丝生成方式为先布置纤维丝中心线,因此当纤维丝半径为0时结构如流程图2最上方所示,仍带有1条线状纤维丝,此时高导热碳纤维含量为0.168%),结构中的孔隙和基体碳采用QSGS生成,参数如式(16)所示,其中核心分布概率cd和方向生长概率Di分别控制结构中孔隙的离散程度和各向同(异)性程度[30]。将孔隙率ε设定为0~30%的随机数字,数据集中L型纤维丝纵向及圆弧部分半径r1、横向部分的半径r2和孔隙率ε不同时,三维结构如图5所示(当r1、r2为9 lu时,结构中的高导热碳纤维含量可达45.09%,而这里采用的QSGS参数可使训练集的样本结构兼具各向同性和各向异性的孔隙,因此采用的训练集在高导热碳纤维和孔隙分布方面具有较好代表性)。 图5 不同r1、r2的纤维丝和孔隙率下的定向热疏导结构三维模型 (16) 测试集1共生成200个尺寸为100 lu×100 lu×100 lu的样本结构,孔隙率变化范围在0~30%之间,分别将纤维丝的r1、r2中的一者大小固定为2 lu,另一者大小分别设定为2、4、6、8 lu,以此定量分析定向热疏导模型中L型纤维丝的纵向和横向取向对热量疏导的作用。 测试集2共生成200个尺寸为100 lu×100 lu×100 lu的样本结构,其纤维丝的r1、r2固定为3 lu,孔隙率设定为0~30%的随机数字,并将其中100个样本结构的QSGS生成时的方向生长概率Di(D1~D26)设定为0.02~0.08的随机数字(其他参数与训练集相同),并将另外100个样本结构QSGS生成时的核心分布概率cd设定为0.001~0.010的随机数字(其他参数与训练集相同)。 测试集3共生成600个尺寸为100 lu×100 lu×100 lu的样本结构,其纤维丝的r1、r2与训练集和验证集相同,依旧采用变化范围为0~9 lu的随机数字,但孔隙率设定为30%~60%(按照5%变化范围为1组,共分为6组)。 采用2.2节所述方法可以轻易地获得3D-CNN需要的样本数据以及由LBM方法计算得到的标签,本文的CNN模型由输入层、卷积层、池化层和输出层组成,通过不同种类的功能层,CNN可以将输入的图像缩小到几个甚至1个参数,同时保持结构的主要特征。具体而言,首先卷积层通过可被视为用具有特定大小的卷积核提取结构的相应特征,通过移动卷积核以提取不同区域中输入图像的特征;然后根据提取出的各个特征生成多个图像,称为特征图。通过池化层,主要特征得以维持并由构成特征图的几个参数表示。总之,应用多个卷积和池化层,逐步提取原输入图像的各种复杂特征,这些特征在特征图中以逐步缩小的尺寸进行表达,大幅减少了深度网络模型的参数数量,从而提高了模型的训练效率。使用全连接层可以将最后一个池化层得到的特征图转换为一维向量,该操作可以看作是特征图和相应内核之间的矩阵乘法。一维向量中的参数表征了原始输入图像的主要特征,可用于建立回归模型。 基于Pytorch框架完成CNN模型的搭建,并且在模型中采用均方误差(MSE)函数作为损失函数,使用自适应矩估计(Adam)[31]作为CNN模型的优化算法,其中的超参数例如学习率经验证集多次调试,最终设定为0.000 1。为了避免简单的线性组合并增加网络的非线性特性,在CNN模型中,选择线性整流函数(ReLU)作为激活函数以在生成预测之前对输出特征进行激活: (17) 通过训练集对模型的训练以及验证集对模型表现的测试,在多次测试选择CNN的主体架构(例如网络深度、功能层的选择等)和超参数之后,最终的3D-CNN的框架图如图6所示,首先应用第1层卷积Conv-1,使用20个不同的5×5×3的卷积核获得包含输入图像20种特征的20个特征通道(即20个特征图),在网络中的4个卷积层中,将卷积核移动的步长(stride)设置为1。为了防止图像边缘信息的缺失及卷积层输出的特征图尺寸缩小,如图7所示将卷积层的扩充参数(padding)设置为(2,2,2),从而在卷积核每次提取结构特征之前将三维特征图最外扩充2层数值为0的张量,这样做是为了避免特征图最边缘的信息在每次卷积过程中只被卷积核扫描一遍,在特征图经过4个卷积层时,图7中H1=H0,W1=W0,D1=D0+2;接着通过池化层Pool-1中2像素×2像素 ×2像素的内核(移动步长设定为2)将特征图的尺寸进一步缩减到输入尺寸的一半。经过4个卷积层和池化层之后,输出特征可以通过全连接层转换为一维特征向量。再经过第2个全连接层的处理后,特征向量将转换为结构的有效导热系数作为输出,卷积神经网络的详细信息如图6和表2所示。 首先,采用平均相对误差(Mean Relative Error,MRE)作为误差函数定量地表示训练后的CNN模型对介观结构有效导热系数预测的精确度,具体表达为 (18) 式中:m为每批训练/验证样本及其标签(即三维定向热疏C/C复合结构及其有效导热系数)中所包含训练/验证样本及标签的个数;kLBM-i为每批样本中第i个结构样本通过LBM计算所得有效导热系数的结果;kCNN-i为每批样本中第i个结构样本通过CNN模型预测所得有效导热系数的结果。 为便于分析比较误差函数与损失函数,对损失函数进行归一化处理,即采用如式(19)所示的均方根误差函数(RMSE)代替损失函数(MSE)进行分析,从而使其变化范围也控制在(0,1]范围内: (19) 在式(18)和式(19)中,分别采用训练集和验证集对图3最终得到的3D-CNN模型进行了训练和预测验证,在CNN模型经过训练集不同代数的训练时,训练集以及验证集的MRE和RMSE的收敛历史曲线如图8和图9所示,可以发现在收敛过程中,不仅二者在训练过程中的变化趋势是同步的,而且二者训练集和验证集的变化也均是紧密同步的,这证明CNN模型从开始得到训练直到收敛的过程中,没有出现过分的过拟合或是欠拟合的现象,验证集的MRE和RMSE在经过1 000步 训练后分别稳定收敛于0.2%和0.5%左右,其结果优于Rong等[22]通过2D切片对3D多孔介质有效导热系数的预测效果(最优CNN模型的MRE和RMSE分别为2.5%和0.8%)。为更加直观地分析采用CNN预测介观结构有效导热系数的效果,将CNN预测值和LBM计算出的结果进行了对比,在验证集的结构样本中,以LBM的计算结果kLBM作为横坐标,以训练后的CNN模型对验证集结构样本有效导热系数的预测结果kCNN作为纵坐标,如图10所示。 图8 最终的3D-CNN模型对于训练集和验证集的MRE随训练代数增加的收敛历史曲线 图9 最终的3D-CNN模型对于训练集和验证集的RMSE随训练代数增加的收敛历史曲线 从图8~图10可以看出,训练集大小为2 000的CNN模型预测结果与LBM结果吻合得很好。为进一步证明深度学习的潜力,整理了传统数值方法和CNN模型的训练/预测过程耗时,如表3所示,可见CNN模型得到训练后,仅需2×10-4h便 图10 验证集的结构样本有效热导率的预测效果 表3 CNN和LBM耗时 可以预测出三维复合结构的有效热导率,相比之下,所采用简化的50×50×50 LBM数值模型计算的平均耗时为2.52 h。 由图10结果可以看出,当样本结构的纤维丝半径和孔隙率都在训练集范围之内时,经训练集训练后的CNN模型可以快速并有效地预测三维定向热疏导结构的有效导热系数。基于此,为快速分析定向热疏导结构内部的L型纤维丝纵向部分半径r1和横向部分半径r2对结构纵向有效导热系数的影响,采用训练好的CNN模型对2.2节所述测试集1样本结构的有效导热系数进行快速预测,分析分别改变结构中L型纤维丝的纵向和横向部分半径时,定向热疏结构纵向有效导热系数的变化情况,并采用测试集的标签检验CNN模型,快速预测出的结果如图11所示,可发现当L型纤维丝纵向部分的半径改变时,介观结构的纵向有效导热系数变化明显;而当L型纤维丝横向部分的半径改变时,介观结构的横向导热系数变化较微弱(且这部分微弱的变化很大程度上是由孔隙率造成的),这侧面说明热量会沿着平行于L型纤维丝的方向被高效疏导至两侧,从而证实了结构中的L型纤维丝对受热面(如图1顶面)热量的定向疏导作用。 图11 测试集1的结构样本有效热导率的预测结果 既然训练后的CNN模型可以非常准确地预测结构参数(如纤维丝半径和孔隙率等)在训练集之内的介观结构有效热导率,对内置L型高导热碳纤维的定向热疏结构中孔隙结构进行研究。为分析当测试结构的参数超出训练样本时CNN模型的预测表现,首先采用测试集2探究了结构中孔隙的离散程度、形状以及各向同(异)性程度较训练集改变时原CNN模型的预测准确性。如图12 所示,Case 1为验证集样本结构;Case 2将结构中孔隙每个方向生长概率Di(D1~D26)设定为0.02~0.08的随机数字(这种Di的设定能使结构兼具各向同性和各向异性的孔,具有较好的代表性);Case 3将结构中孔隙的核心分布概率cd设定为0.001~0.010的随机数字,从而改变结构中的孔隙离散程度。图12中柱状图为3种孔隙结构有效热导率CNN预测的相对误差,可以发现,当QSGS中参数较训练集做出较大改变时,预测的相对误差依旧可控制在0.500%以内,这验证了本文训练集样本结构的QSGS参数较具代表性。对纤维半径为3 lu,孔隙率为15%、20%和25%,结构中3种孔隙分布情况下的有效导热系数进行数值计算,结果如图12中3种颜色点所示,发现3个Case在相同孔隙率下有效导热系数波动范围几乎一致,因此孔隙的各向同(异)性和离散程度对结构有效热导率影响甚微,而结构的孔隙率对结构有效导热系数影响较大。 图12 分别改变QSGS参数Di和cd从而改变孔隙的各向同(异)性程度(Case 2)和离散程度(Case 3)时CNN预测的相对误差和孔隙率为15%、20%、25%时结构有效热导率变化情况 利用2.2节所述的测试集3检测当定向热疏结构的孔隙率超出训练集为30%~60%时,CNN模型对测试样本结构有效导热系数预测的效果。如图13柱状图红色部分所示,当测试样本结构的孔隙率超出训练样本结构0~30%的孔隙率时,测试结果的相对误差(MRE)将逐渐增大,在孔隙率为30%~35%和35%~40%时,MRE分别仅为1.79%和4.32%,这证明了CNN模型的强大学习能力,但随着测试样本结构孔隙率逐渐超出40%以上,相对误差将会变得越来越大,在孔隙率为55%~60%时其数值将会达到30%以上,图14中红色点以LBM计算出的有效热导率为横坐标,以训练样本结构孔隙率为0~30%的CNN模型预测结果为纵坐标,通过观察这些点与直线y=x的距离可以直观形象地体现这种误差随孔隙率的变化趋势。为克服CNN模型“外推”会将存在较大误差的现象,尝试使用相同大小且具有更大孔隙率跨度的训练集,以期将测试集孔隙率这一结构参数以“内插”的形式包含在训练集范围内,具体预测误差和结果如图13柱状图黑色部分和图14黑色点所示。 图13 测试样本孔隙率为30%~60%、训练集大小不变时新、旧CNN模型预测结果相对误差 图14 定向热疏结构孔隙率为30%~35%和40%~45%时新、旧CNN模型的预测结果 综上,通过比较图13和图14红色和黑色部分,可以得出结论:虽然CNN模型在LBM传热计算上表现出强大的学习能力,但这种学习能力在测试样本结构过分超出训练集时不再可靠,当孔隙率变化范围从30%~35%变化到55%~60%时,CNN模型的“内插”预测相对误差将较模型“外推”降低0.93%~30.72%。 提出了采用高导热碳纤维丝将飞行器表面热量高效定向疏导至低温区域的定向热疏导介观模型,并且通过深度学习方法预测了这种定向热疏复合结构的有效导热系数,大幅减少了有效导热系数的计算时间,实现了对内置L型高导热碳纤维丝的定向热疏结构纵向有效热导率的快速精准预测,并得出以下结论: 1) 采用3D-CNN预测三维介观结构有效导热系数时,将三维LBM数值模型直接作为CNN的输入样本结构可以克服三维结构难以捕捉的问题,从而提高了预测准确性。 2) L型纤维丝的纵向部分半径对定向热疏结构的纵向有效热导率影响较大,而横向部分对结构的纵向有效热导率影响很小,侧面表明了热量沿着L型高导热碳纤维丝方向被定向疏导至结构两侧。 3) 当测试集孔隙率超出训练集的5%和10%时,预测的相对误差分别为1.79%和4.32%,证明了CNN模型具有强大学习能力。为解决孔隙率外推预测误差较大的问题,提出并证明了在训练集大小保持不变时,通过增加训练集孔隙率跨度能大幅减少预测的相对误差。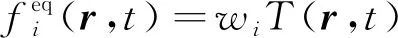
2 3D-CNN预测有效导热系数
2.1 3D-CNN的3D样本生成
2.2 数据集

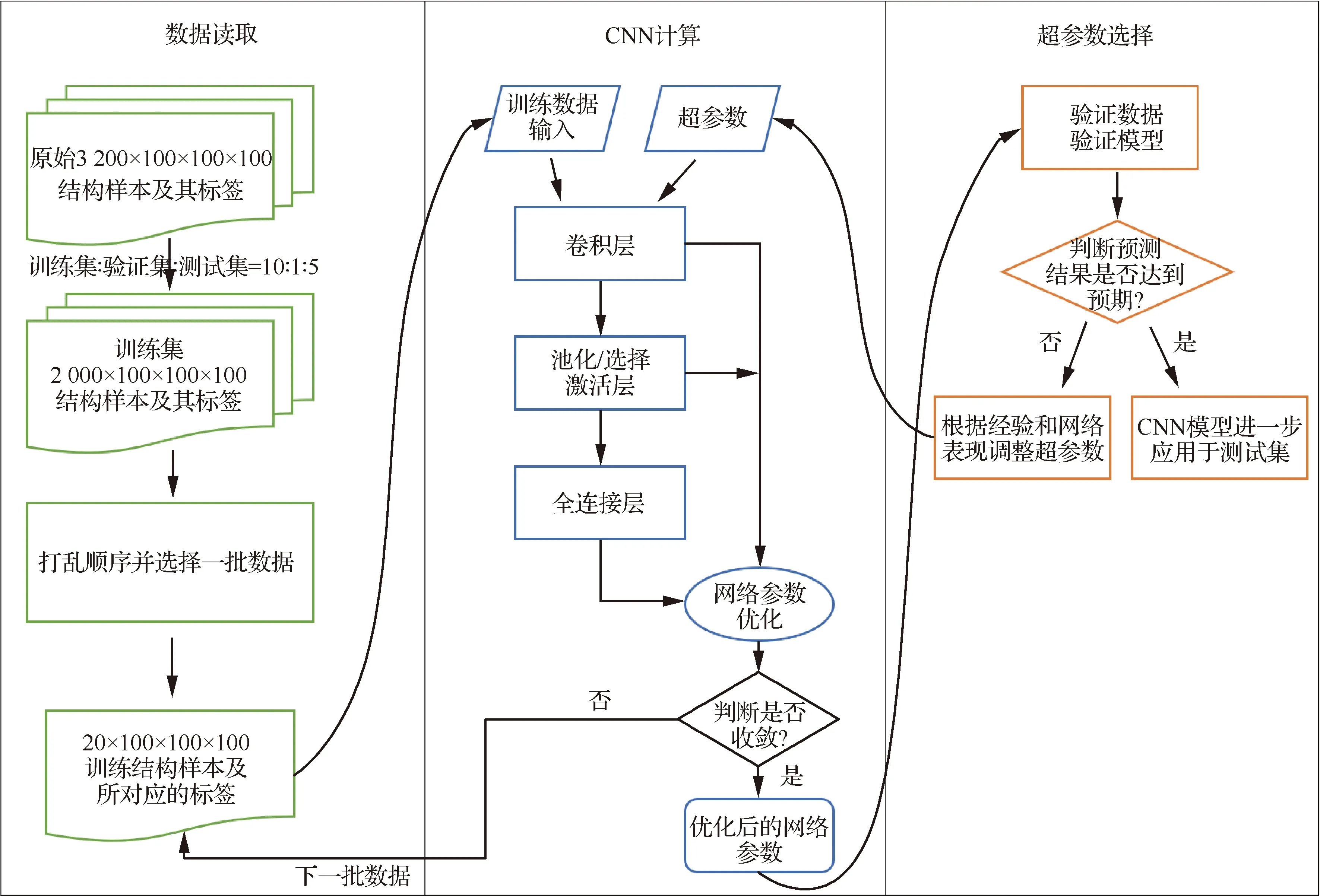
2.3 3D-CNN的计算过程
2.4 3D-CNN验证结果
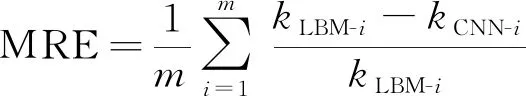

2.5 3D-CNN的测试结果
3 总 结
