偏序集上的相对定向集及其应用

刘东明，姜广浩，李 辉

(淮北师范大学数学科学学院，安徽淮北 235000)

1 预备知识

自20世纪70年代著名数学家和逻辑学家Scott创立连续格理论[1]以来，经过多年的发展，连续格的大部分研究成果被推广到连续Domain上，并在范畴学、格论、格上拓扑以及计算机程序理论上得到广泛应用[2-4].白仲林[5]提出了“一致集”的概念，这一概念是“定向集”的自然推广，有关于一致集的格论研究是程序展开理论的基础.近年来，阮小军[6-8]对一致连续偏序集做了深入研究并得到十分丰富的成果.受“一致集”概念的启发，本文首先在偏序集上引入并考察相对集的概念，讨论其性质，并证明当T定向时，偏序集上所有相对T的定向集可以构成一个完备格.其次，在相对定向集基础上引入相对定向完备集的概念，得到的一致完备集是相对定向完备集，并研究定向完备集、一致完备集与相对定向完备集三者之间的关系.本文中大部分采用文献[2]的符号.

定义1.1[2]设P为偏序集，D⊆P，D≠∅，对于任意x，y∈D,sup{x,y}存在且sup{x,y}∈D，则称D为偏序集P上的定向集.

定义1.2[5]设P是偏序集，S⊆P，若∀x,y∈S，存在z∈P，使得x≤z,y≤z，则称S为P的一致集.

定义1.3[2]设P为偏序集，若对于任意定向子集D,supD存在且supD∈D，则称偏序集P是定向完备的.简记为DCPO.

定义1.4[5]设P为偏序集，若对于任意一致集S，supS存在且supS∈S，则称偏序集P是一致完备的.简记为UCPO.

2 相对定向集

定义2.1 设P是偏序集，S,T⊆P，S≠∅，T≠∅，若∀x,y∈S，存在t∈T，使得x≤t,y≤t，则称S为偏序集P相对于T的定向集.当T明了时，简称S为相对定向集.

设P为偏序集，集合T⊆P，T≠∅，记Ir(T)={↓S:S为相对于T的定向集}，U(T)={S:S为相对于T的定向集}.

注2.1 相对定向集不一定为下集，下集也未必是相对定向集.

注2.2 定向集不一定为相对定向集，相对定向集也未必为定向集.

例2.1 设P={a,b,c,d,e,f,g}，若取T={b,e,f,g}，令S={c,d,f}，则S为相对T的定向集，但是S不是定向集也不是下集；令M={a,b,c,f,g}，则可见M本身为定向集且为下集，但M不为相对T的定向集.

定理2.1 设P为偏序集，集合T⊆P，T≠∅，S为相对T的定向集，则S为偏序集P上的一致集.

证明 设S为相对T的定向集，根据定义有∀x,y∈S，存在t∈T，使得x≤t且y≤t，又T⊆P，故t∈T，由一致集的定义可得，S为偏序集P上的一致集.

注2.3 若S为偏序集P上的一致集，S未必是偏序集P相对T的定向集.

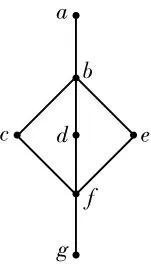
例2.2 如图1所示，设P={a,b,c,d,e,f,g}，取T={e,f,g}，S={c,d,f,g}，则S为偏序集P的一致集，但S不为P相对T的定向集，且S本身不为定向集.

下面定理揭示了定向集、相对定向集和一致集合的内在联系.

命题2.1 设P为偏序集，T,S⊆P；T,S≠∅，则有如下结论成立：

(1)若T=S，则S相对T定向⟺T本身定向；

(2)若T=P，则S相对T定向⟺S为P中的一致集.

命题2.2 设P为偏序集，T⊆P，T≠∅，则以下结论成立：(1)∀x∈T，则{x}∈U(T)；(2)∀x,y∈T，若x≤y，则{x,y}∈U(T).

证明 (1)∀a,b∈{x}，有a,b=x∈{x}⊆T，{x}为相对T的定向集，即{x}∈U(T).

(2)∀a,b∈{x,y}，有a,b取值只可能为x或y，又x≤y∈T，有a≤y,b≤y，从而{x,y}为相对T的定向集，即{x,y}∈U(T).

定理2.2 设P为偏序集，T⊆P，T≠∅，则Ir(T)⊆U(T).

证明 任意取M∈Ir(T)，则存在S∈U(T)，使得M=↓S.∀x,y∈M，则x,y∈↓S，从而存在s1,s2∈S，使得x≤s1,y≤s2，又S为相对于T的定向集，故存在t∈T，使得s1≤t,s2≤t，进而有x≤t,y≤t，所以M为相对T的定向集.

引理2.1 设P为偏序集，T⊆P，T≠∅，S1⊆S2，若S2∈U(T)，则S1∈U(T).

证明 ∀x,y∈S1，因S1⊆S2,故x,y∈S2,又S2∈U(T),所以存在t∈T,使得x≤t,y≤t，进而S1∈U(T).

定理2.3 设P为偏序集，T⊆P，T≠∅，S1,S2∈U(T)，则S1∩S2∈U(T).

证明 因为S1∩S2⊆S1，由引理2.1可得S1∩S2∈U(T).

定理2.4 设P为偏序集，T⊆P，T≠∅，S1,S2∈U(T)，若T定向，则S1∪S2∈U(T).

证明 ∀a,b∈S1∪S2，则a属于S1或者S2，b属于S1或者S2，如果a,b同时属于S1或者a,b同时属于S2，则结论成立；下证a,b不同时属于一个集合时，结论也成立，不妨令a∈S1且b∈S2，因S1,S2都为相对T的定向集，故分别存在ta,tb∈T使得a≤ta,b≤tb，因为T定向，所以存在t∈T使得a≤t,b≤t故S1∪S2为相对T的定向集，即S1∪S2∈U(T).

上述定理2.3和定理2.4可以推广到任意多个情形.

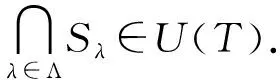
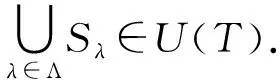
由定理2.5和定理2.6可以得到定理2.7.

定理2.7 设P为偏序集，T⊆P，T≠∅，T定向，则U(T)为完备格.

3 相对定向完备集

定义3.1 设P是偏序集，T⊆P，T≠∅，若任意相对T的定向集都存在最小上界，则称P为相对T的定向完备集；当T明了时，简称P为相对定向完备集.简单记为RDCPO(T).

引理3.1[5]设P为偏序集，∀D⊆P，若D为定向集，则D为一致集.

定理3.1 设P为一致完备集，则P即为定向完备集也为相对定向完备集.

证明 一方面，∀D∈P，D≠∅，若D定向，则D为一致集，又P为一致完备集，故supD存在且supD∈D，进而P为定向完备集.

另一方面，∀D∈P，D≠∅，若D相对T定向，则由引理3.1知，D为一致集，因为P为一致完备集，所以supD存在且supD∈D，进而P相对定向完备集.

定理3.2 设P是偏序集，T⊆P，T≠∅，若T=P则P为相对T的定向完备集当且仅当P为一致完备集.

证明(必要性)∀D⊆P，D为一致集，因T=P，由命题2.1可知，此时的D相对T定向，又P为相对T定向完备，故D存在最小上界，从而P为一致完备集.

(充分性)∀S⊆P，S相对T定向，由定理2.1可知，S为一致集，此时P为一致完备集，故supS存在且supS∈S，进而P为相对T定向完备集.

定理3.3 设P为一致完备偏序集，∀D⊆P，则D为一致集当且仅当D为定向集.

证明(必要性)∀D⊆P，设D为一致集，因P为一致完备偏序集，故supD存在且supD∈D，从而对于∀x,y,y∈D，有x≤supD,y≤supD，即D为定向集.

(充分性)∀D⊆P，设D为定向集，由定理2.1可得，D为一致集.

注3.1 一致完备集的子集未必是一致集.

例3.1 图2为一致完备集，但它本身不是一致集.

命题3.1 设P为一致完备偏序集，T⊆P，T≠∅，若∀D⊆T，则D为相对T的定向集当且仅当D本身为定向集.

证明(必要性)∀D⊆T⊆P，设D相对T定向，由定理2.2可得，D为一致集，又P为一致完备偏序集，故supD存在且supD∈D，从而对于∀x,y∈D，有x≤supD,y≤supD，故D为定向集.

(充分性)∀D⊆T⊆P，设D为定向集，由定理2.1可得，D为一致集，又P为一致完备偏序集，故supD存在且supD∈D⊆T，从而∀x,y∈D，存在t=supD∈T，使得x≤t,y≤t，所以D为相对T的定向集.

结合定理3.3和命题3.1得到定理3.4.

定理3.4 设P为一致完备偏序集，T⊆P，T≠∅，若∀D⊆T，则下列结论等价：(1)D为相对T的定向集；(2)D为定向集；(3)D为一致集.

注3.2 若P为定向完备集，P未必为一致完备集.

例3.2 如图3所示，设P=N∪M,其中N=[a,b],M={c,d,e,f}，规定P中的序：若∀x,y∈N，则x≤y⟺x=y；若x∈M，y∈N,则x≤y；若x,y∈M则按通常的序.易证P为定向完备集，M⊆P为一致集，但supM∉M，故P不是一致完备集.

注3.3 若P是相对定向完备集，P也未必为定向完备集.

例3.3 如图4所示，设P=[b,a)∪{d,c,e}，取T={d,c,b,e}，则∀D∈P，若D相对T定向则D存在最小上界，从而P为相对T的定向完备集，但是P不是一个定向完备集.

注3.4 若P为相对定向完备集，P未必是一致完备集.

例3.4 如图3所示，当T={b,e,f}时，此时的P为相对定向完备集，但由例3.2知，P不是一致完备集.

注3.5 若P为定向完备集，P未必为相对定向完备集.

例3.5 在图1中，P={a,b,c,d,e,f,g}，令T={b,e,f,g}，易知P为定向完备集，但是当取D={c,d,f,g}时sup{D}={b}不属于D，故P不是相对定向完备集.

综上所述可以得到，DCPO、UCPO、RDCPO(T)三者关系如图5所示.