核心素养理念下的变式教学研究

林慧妮

摘 要：随着教育改革的不断发展，人们越来越重视对学生核心素养的培养。由于数学的学科特点以及传统教学模式的不足，学生数学学习的主动性不够，导致教学效果并不显著。所以，教师需要不断地进行新的教学方式的尝试和研究，提高学生的课堂参与度。基于此，笔者将结合自身的教学经验，对核心素养理念下的变式教学的原则和应用进行探究。

关键词：初中数学;核心素养;变式教学

初中作为人生的一个重要阶段，初中教育肩负着提升学生基本素养，打好学生人生底色中重要任务。由于时代的高速发展，人们生活水平的日益提高，在享受便利生活方式的同时，学生也变得越来越浮躁，学习也想要找捷径。显然，这样是不可能学好数学的。所以，对于数学这门学科的态度并不十分友好。因此为了改善这一现状，本文对核心素养理念下的变式教学进行探究。

一、变式教学法的原则

（一）主体性原则

传统的教学模式主要是以教师为中心，单方面向学生讲授课本知识的教学形式。由于学生始终处于被动学习的状态，导致学习热情不够，课堂参与度低，这样的学习效果是低效的。所以要进行有效的变式教学，应该坚持学生的主体性原则，通过创设有趣的问题情境，激发学生的学习兴趣，把学习的主动性交给学生，由学生作为学习的主体。教师在教学过程中，应该充当引导者、辅助者的角色，通过设计合适的教学内容，引导学生独立思考，将教学重点放在启迪学生的理性思维能力，以及对学生解法的即时评价上。鼓励学生积极思考，体会到解题的乐趣，爱上数学。

（二）思想性原则

变式教学是培养学生深度思维能力的重要途径，变式的有效设计可以充分的促进深度学习的开展。教师在进行变式教学中，应该时刻记得要以数学思想作为引领，通过变式教学，指导学生学会一题多变，一题多解，多题归一，继而做到举一反三，以少胜多[2]。这样的变式教学，既可以充分激发学生的学习热情，又能引导学生积极思考解决问题的方法，甚至是从多角度，多方向的解决问题。让学生勇于面对生活中出现的问题，并能用数学的思维解决实际生活中出现的问题，实现学生核心素养的培养。

二、变式教学的应用

（一）概念课的变式教学

数学概念是数学学习的基本内容，是掌握数学基础知识的前提。许多学生对于数学概念的学习不重视，以为只要能解题就行了。事实上，概念的理解不清，会导致学生无法灵活的应用概念解答问题，从而在解题时产生不必要的失分。所以在进行概念教学时，可以通过变式教学，加强学生对概念的理解，把握概念的本质意义，进而能够灵活的应用知识解决问题。

例如，在进行《锐角三角函数》的概念教学时，笔者设计了这样的一系列问题情境：

问题1：在Rt△ABC中，∠C=90°，∠A=30°，BC=35m，求AB的长.

问题2：在上述条件下，BC=50m，你能求AB的长吗？为什么？

师生总结：在直角三角形中，30°角的对边与斜边的比值等于，是一个固定值。

发现问题：其他锐角的对边与斜边的比值是否也是一个固定值呢？

问题3：在Rt△ABC中，∠C=90°，∠A=45°，∠A的对边与斜边的比值是一个固定值吗？如果是，是多少？

问题4：当∠A取其他一定度数的锐角时，它的对边与斜边的比是否也是一个固定值？证明你的结论？

问题5：当锐角∠A的取值不同时，它的对边与斜边的比值有可能会相同吗？你有什么发现？

这些问题始终围绕着正弦函数的概念展开，不断变化，层层递进。笔者基于学生的基本学情，在学生熟悉的知识点设问，激发学生学习热情，引导学生参与到课堂活动中，成为学习的主体。学生在思考回答变式问题的过程中，通过旧知识的正迁移，由浅入深，发现正弦函数的本质，以锐角作为自变量，当锐角确定时，其对边与斜边的比值就是一个固定值，且由锐角的取值唯一确定，从而能够更加深刻的理解正弦函数中“函数”的意义。这种通过解决问题获得的知识，既印象深刻，又能让学生感受到学习的乐趣，两全其美。

（二）复习课的变式教学

复习课，作为课堂教学的一个重要课型，对学生系统掌握知识，发展思维能力是非常必要的。但是要想真正上好一节复习课确实不容易。在实际教学中会发现，很多复习课都是按照“复习知识点—做题—讲评”的过程展开。这样的教学设计，很容易在学生已会的地方花费太多的时间，却在掌握不够的地方匆匆略过。而且，有些复习课很像习题课，整节课就是让学生不停地做题，然后听教师讲评。整个教学过程，学生无法感受到学习的乐趣，达不到预期的效果。所以，教师可以尝试用变式教学的方式开展复习课。

例如，在进行二次函数图像和性质复习课教学时，笔者设计了如下设计：

问题1：你能写出一个二次函数解析式吗？

问题2：你能画出它的函数图像并说出它的性质吗？

问题3：令y=0，你能得到相应一元二次方程的解吗？

问题4：你能根据函数图像，直接写出y>0时，自变量的取值范围吗？

问题5：y有最值吗？当自变量取值有范围限制时，你能求出此时函数的最大（小）值吗？

问题6：你能不能利用二次函数的图像和性质的相关知识，再设计一些问题考同学们呢？

问题7：如果给出的是一个含有参数的二次函数解析式，你又能设计一些怎样的问题呢？

对于复习课的展开，通常教师都是先进行知识点的复习，然后通过讲解例題来复习和巩固知识点，这样的传统授课形式，容易让学生产生困倦感，所以，笔者的想法是，先通过设计变式性的问题，让学生自觉的成为学习主体，增加学生的课堂参与度。接着通过设计变式性的问题，引导学生自己设计问题，解决问题。通过这样的变式教学，既能够巧妙的引导学生复习了教学知识点，又能够形成系统的知识体系，培养的较强的解决问题的能力。

（三）习题课的变式教学

把变式理念融入到课堂的练习设计与训练中，可以有助于学生更好的理解知识的本质，明白“万变不离其宗”的数学道理，真正的掌握数学解题方法和数学思想[3]。下面笔者以自己设计的课堂练习题为例予以展示：

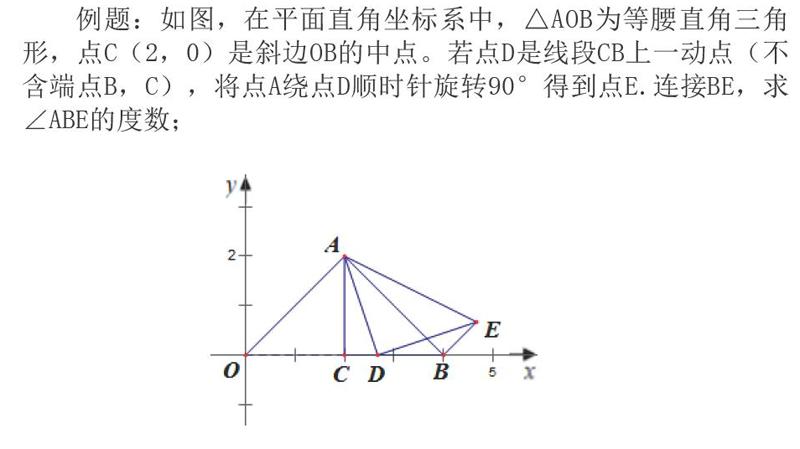
例题：如图，在平面直角坐标系中，△AOB为等腰直角三角形，点C（2，0）是斜边OB的中点。若点D是线段CB上一动点（不含端点B，C），将点A绕点D顺时针旋转90°得到点E.连接BE，求∠ABE的度数;

变式1：点D是线段OC上一动点（不含端点C），求∠ABE的度数.

变式2：点D在x轴正半轴上，有相同的结论吗？点D在x轴上呢？

变式3：若点A是绕着点D逆时针旋转90°得到点E，则是否也存在着某个角为定角，你能找到吗？

这个变式题虽然题目在不断的变化，可是本质上都是考查“K”型全等的基本模型和等腰直角三角形的基本性质，教师在进行变式教学时，可以先针对这两个知识点予以复习讲解，然后给学生充分的时间进行原题的思考，在学生充分思考做题的前提下，教师予以点拨指导，对于大部分同学来说，变式1就能举一反三完成了。变式2和变式3难度较大，特别是变式3，对学生的思维要求比较高，可以作为课后思考题，引发学生课下继续思考，达到深度思维的训练。当然如果学生程度一般，也可直接省去变式3。至于变式2，虽然难度较大，但是由于已经有了教师对原题和变式1的讲解，可以将题目的解题思路明朗化，题目的难度也就随之降低，基本上能达到训练学生较难题的目标。培养学生不畏难，敢于战胜困难的核心素养。

以上都是笔者结合自身的教学经验，对核心素养理念下变式教学的尝试和研究。总之，在如今这个飞速发展的时代，教师应当与时俱进，充分挖掘和发挥变式教学在实际教学中的优势，提高学生的课堂参与度，切实有效的培养学生的核心素养。

参考文献

[1]彭会君.基于数学核心素养的初三复习课的有效教学研究[D].武汉：华中师范大学，2019.

[2]花奎，丁良栋.数学思想做引领 变式探究促深度——一道三角形面积最值问题的变式教学及思考[J].中学教研（数学），2020（12）：1-6.

[3]劉文梅.浅谈数学教学中的几种变式训练[J].数学学习与研究，2020（17）：68-69.