克劳斯工业催化剂模拟与结构优化设计

张素娟，李金金，温崇荣，朱宏扬，岳海荣，刘长军

（1. 中国石油西南油气田公司天然气研究院 天然气净化研究所，四川 成都 610213；2. 国家能源高含硫气藏开采研发中心，四川 成都 610213；3. 四川大学 化学工程学院，四川 成都 610065）

煤热解、气化、焦化、石油炼制和天然气净化都产生大量含H2S的尾气[1-6]。 克劳斯硫磺回收工艺主要通过反应式(1)和反应式(2)将H2S转化成单质硫固体并回收热量[7,8]。 改良克劳斯硫磺回收工艺应用最广泛，其包括了高温热反应和低温催化反应两个阶段[7,9]，其中低温催化反应对于提高整个工艺的硫磺回收率至关重要，而催化剂是克劳斯硫磺回收工艺的核心技术[9]。 氧化铝是工业中应用最广泛的克劳斯催化剂，多为直径4~6 mm的球形或圆柱形颗粒[10]。催化克劳斯反应是以生成S6和S8单质为主的强放热反应，因此颗粒内的传热和传质对该气固催化反应过程影响显著。

克劳斯工业催化剂颗粒的有效因子通常只有20%左右[11-13]。催化剂颗粒的几何结构和尺寸是影响气固催化反应中反应物、产物以及热量在催化剂内部传递的重要因素[14]。优化催化剂尺寸，改进催化剂结构能够有效地提高催化剂效率[15-17]。 工业克劳斯催化剂结构的优化设计对提高克劳斯脱硫工艺效能具有重要意义。 对于球形和圆柱形催化剂颗粒上符合一级不可逆反应动力学的等温反应过程，可以通过理论推导得到催化剂颗粒的有效因子[14]。但是，通常认为克劳斯反应对H2S是一级反应，对SO2是0.5级反应，本征反应速率可由式(3)表示[12]。而非一级不可逆反应的扩散-反应方程（式(4)）无解析解，因此不能通过数学分析方法确定扩散影响程度[14,15]。 而过多简化的模型又大大降低了模型的准确性[15]。

本文采用计算流体力学理论构建了不同尺寸和几何构型的克劳斯催化剂三维稳态模型，通过耦合传质-传热多物理场求解研究了反应温度、克劳斯反应本征速率、催化剂尺寸、孔隙率、孔径以及几何结构对克劳斯催化剂催化效率的影响，进而指导克劳斯工业催化剂的改进和优化设计。

1 克劳斯催化剂模拟

1.1 催化剂模型

1.1.1 几何模型及网格划分

克劳斯催化剂通常为直径6 mm的球形γ-Al2O3。因此首先通过COMSOL Mutliphysics几何建模工具构建了不同直径的三维球形催化剂颗粒模型（图1a）。为考察几何构型对催化剂有效因子的影响[18]，基于等体积原则建立了与6 mm球形颗粒等体积的圆柱形、 单孔圆柱形、5孔圆柱形以及9孔立方体形的催化剂几何模型（图1）。 网格划分采用四面体网格，最大网格尺寸为0.33 mm，最小网格尺寸为0.024 mm，球形模型的四面体网格数为25949， 求解自由度为90038。 经验证进一步细化网格不影响模型计算精度，网格独立性好。

图1 克劳斯催化剂颗粒几何模型

1.1.2 数学模型及边界条件

假设催化剂颗粒内各向均匀，颗粒内扩散服从费克第一定律，系统处于稳态，且外扩散阻力可忽略不计。 通过物料和热量衡算可建立催化剂内各物质的扩散和传热方程（式(5)和式(6)）。

式中，i为H2S、SO2、S2、S6、S8或H2O，下同。

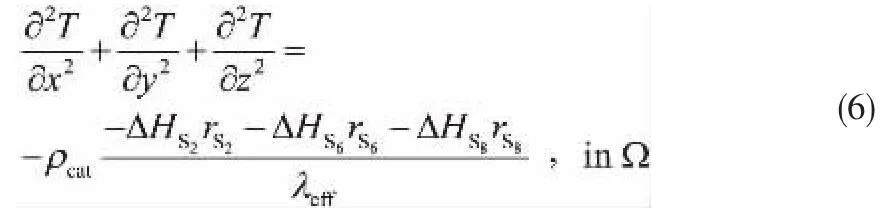
忽略外扩散阻力的影响，催化剂外表面采用浓度和温度边界条件。 催化剂颗粒外表面各物质浓度和温度与气相主体的浓度和温度相同（式(7)和式(8)）。

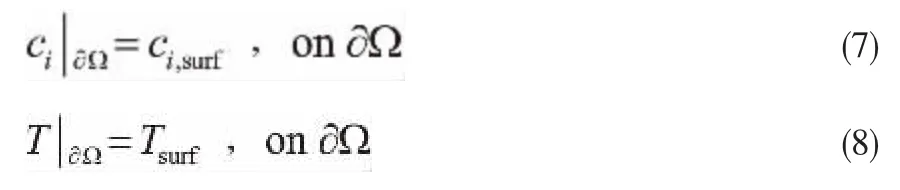
气体主体浓度采用工业上第一级克劳斯反应器的进口物料组成，见表1。

表1 反应器进口物料组成

当内扩散影响严重时，浓度梯度和温度梯度并非在催化剂中心处才降为零，而是浓度梯度和温度梯度分别在催化剂中的某一位置区域ΩD和Ω’D内已经为零， 此区域内实际已无宏观反应和传热进行，即式(9)和式(10)。

式中，Ω为求解区域，ΩD和Ω’D分别为求解区域的温度和浓度死区，∂Ω为求解区域Ω的边界。

1.2 模拟参数及算法验证

1.2.1 有效扩散系数

一般克劳斯催化剂的孔道直径远大于气体分子直径，因此可忽略构型扩散的影响。 克劳斯催化反应温度较高，催化剂颗粒两侧的压降极小。 因此忽略表面扩散和层流流动，仅考虑分子扩散和努森扩散，以及催化剂内温度和气体组成的变化对催化剂内有效扩散系数的影响（式(11)）。 其中，努森扩散系数由式(12)计算，分子扩散系数由式(13)计算。

式中，yi是催化剂内组分i的物质的量分数；εp为催化剂的孔隙率；τ为催化剂的曲折因子；dpore为催化剂的平均孔径，m；Mi为相对分子量。

二元组分i，j的分子扩散系数Dijeff由式(14)和式(15)计算。

式中，pt为总压强，Pa；Vi为Fuller定义的分子扩散体积[20]。

1.2.2 有效导热系数和混合气体比热容

催化剂颗粒的有效导热系数由催化剂骨架结构和孔内气体导热系数共同决定。 多孔催化剂颗粒的有效导热系数可由式(16)计算[21]。

式中，N为催化剂孔内气体组分数，λs为催化剂骨架导热系数，W/(m·K)。

Al2O3载体在不同温度T下的导热系数由式(17)计算得到[21]。

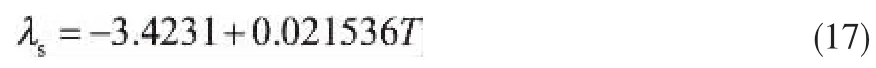
催化剂孔内单组份气体导热系数λfi由式(18)计算得到。

式中，λgi为纯组分i导热系数，W/(m·K)；L为分子平均自由程，m；Cp和Cν分别为气体的定压比热容和定容比热容，J/(kg·K)。

混合气体的比热容Cmix由各纯组分的比热容通过式(19)计算得到。

式中，Cpi为各组分纯物质的定压比热容，单位为J/(kg·K)；A、B、C、D为各物质的计算常数[22]。

1.2.3 克劳斯反应动力学

在催化剂有效因子计算中需要选用正确的本征动力学方程。 克劳斯催化反应动力学的研究表明，氧化铝催化剂表面的物理结构对克劳斯催化反应机理影响甚微[13,23-25]。 Quet等[24]提出了氧化铝催化的克劳斯反应的本征反应动力学，并将水分影响纳入反应动力学方程（式(21)）。

Abdel-Fattah等[19]结合克劳斯硫回收装置的工业数据进一步从式(21)建立了S2、S6和S8三个产物的生成动力学方程（式(22)~式(24)），并将其用于克劳斯工业催化反应器的模拟，其结果与装置工业运行数据吻合。 因此本文采用式(22)~式(24)所示的本征反应动力学方程来对克劳斯催化剂颗粒进行研究。

式中，k01，k02和k03为指前因子，其值分别为0.0773，2.76和5.52。

1.2.4 催化剂有效因子计算

内扩散有效因子根据其定义由式(25)计算。

式中，rΩ为催化剂外表面反应速率，mol/(m3·s)；V为催化剂颗粒体积，m3；r为催化剂内的反应速率，mol/(m3·s)。

1.2.5 模型求解及算法验证

根据文献[12,13]，以商品化的直径为6 mm，孔隙率为0.6，平均孔径为2.5 nm，颗粒密度为1.24 g/cm3的球形氧化铝催化剂为基础，建立催化剂模型（图1a）。在表2所示反应条件下对该氧化铝催化剂的克劳斯反应数据进行求解， 并计算得催化剂有效因子为0.145，与文献数据0.14吻合，证明本文所建模型和采用的计算方法正确有效。

表2 6 mm氧化铝催化剂有效因子

2 结果与讨论

利用前述模型及方法，对影响工业克劳斯催化剂有效因子的各因素逐一进行考察。

2.1 反应温度的影响

在改进的克劳斯工艺中通常采用逐级降温的串联反应器流程。 因此首先考察了反应温度对克劳斯催化剂有效因子的影响，如图2所示。

图2 反应温度对克劳斯催化剂有效因子的影响

图2表明，当反应温度由463.15 K升高到563.15 K时，克劳斯催化剂的有效因子从0.292降至0.176。 这是因为克劳斯反应的活化能较大，温度对反应速率的影响比对传质速率的影响大。 升高温度，反应物反应速率比其在多孔介质中的扩散速率增加更快。多级克劳斯反应器中，第一级克劳斯催化反应的反应温度高，末级反应器温度低，因此末级反应器中催化剂的有效因子高于前端反应器中催化剂的有效因子， 但总体上克劳斯催化剂的有效因子很小，有很大的提升空间。

2.2 本征反应速率的影响

虽然克劳斯催化反应机理对Al2O3表面的物理结构不敏感，但克劳斯反应本征反应速率仍然由催化剂本征活性决定。 因此以式(22)~式(24)描述的本征反应速率方程为基准，考察了当催化剂活性发生变化， 即本征动力学方程的指前因子发生变化时，典型克劳斯催化剂有效因子的变化规律，结果如图3所示。 当其他反应条件不变，催化剂本征反应速率常数增大20%时， 其有效因子从22.1%下降至约20.5%；当本征反应速率降低20%时，其有效因子从22.1%提升至24.2%。 图3表明有效因子的变化趋势与催化剂本征活性的变化趋势相反。 因为当催化剂的本征反应速率增大， 活性位上的转化频率加快，反应物的消耗速率加快，而扩散传质速率不变的情况下，反应物的扩散距离更短，因此催化剂内起催化作用的部分变小，催化剂有效因子降低。 此外，当催化剂本征催化活性在较小范围内出现波动时，有效因子的变化能够抵消一部分本征活性变化带来的影响。 因此受有效因子的影响，单纯提高克劳斯催化剂的本征活性并不能显著提高工业克劳斯催化剂颗粒在反应器的催化效率。 提高有效因子是提高克劳斯催化剂效率的关键。

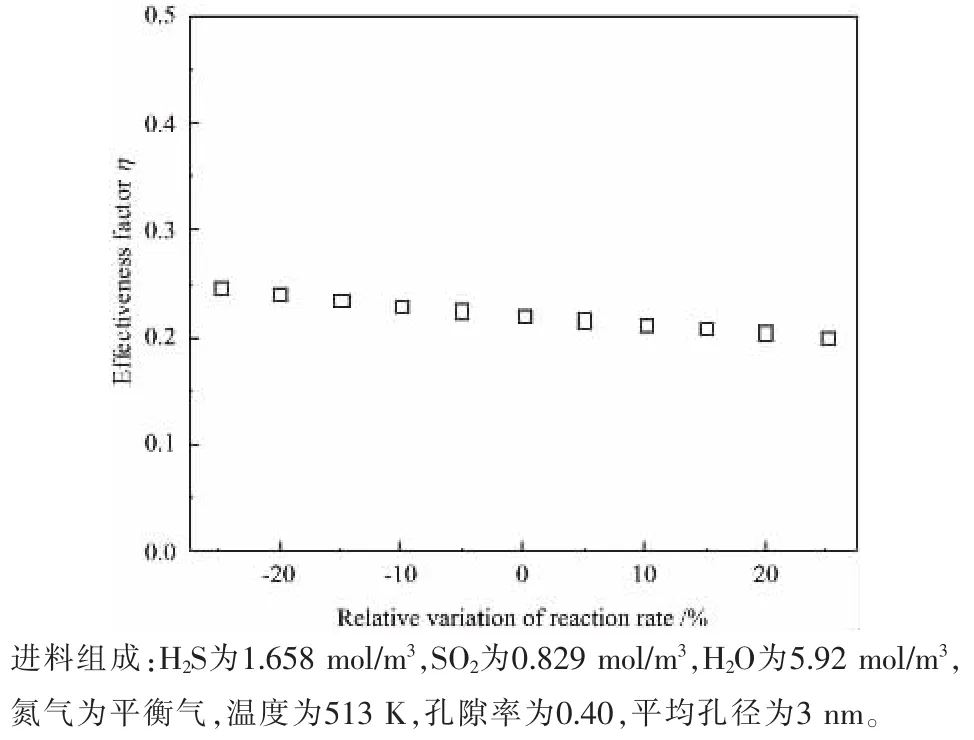
图3 本征反应速率常数对克劳斯催化剂有效因子的影响

2.3 催化剂尺寸的影响

首先考察了球形克劳斯催化剂有效因子随颗粒直径的变化规律，结果如图4所示。 图4表明，克劳斯催化剂的有效因子随着催化剂颗粒尺寸的增大而迅速减小。 直径为0.20 mm的球形催化剂颗粒，其有效因子为98.5%， 当催化剂直径增大到10.00 mm时，催化剂有效因子降为14.8%。 这主要是因为克劳斯反应速率比传质速率快，在扩散传质距离不变的情况下，增大催化剂颗粒直径导致反应物不能接触的体积增大，即催化剂内部死区增大，进而有效因子降低。 同时也证明，在进行克劳斯催化剂本征催化活性测定时，克劳斯催化剂必须破碎至200~300 μm以下才能有效地避免内扩散对反应速率的影响。

图4 催化剂尺寸对克劳斯催化剂有效因子的影响

2.4 催化剂孔隙率的影响

催化剂颗粒内的孔隙是反应物分子和产物分子的扩散通道。 孔隙率的高低是影响反应物和产物扩散的重要因素。 图5考察了催化剂颗粒的孔隙率在较大范围内变化时， 催化剂有效因子的变化规律。 图5表明，催化剂颗粒的有效因子随着孔隙率的增大而增大。 当颗粒的孔隙率从0.20提高到0.80时，催化剂的有效因子从0.168提升到0.293。 这是因为催化剂颗粒内的扩散通道随着孔隙率的增大而增加，促进了反应物向催化剂内部的深入扩散，使得催化剂的利用率提高。 虽然提高克劳斯催化剂的孔隙率能够提高催化剂的有效因子，但孔隙率由现有工业克劳斯催化剂的约0.40提高到0.80，有效因子也仅从0.221提高到0.293。 因此通常情况下催化剂生产中颗粒孔隙率即便发生小的波动，其对催化剂整体性能的影响也很小。 单纯提高孔隙率不是提高克劳斯催化剂效率的最有效的手段。

图5 催化剂孔隙率对克劳斯催化剂有效因子的影响

2.5 催化剂孔径的影响

催化剂颗粒内微观孔道的大小直接决定了反应物分子和产物分子在催化剂内扩散传质类型和传质速率。 图6为催化剂孔径对克劳斯催化剂有效因子的影响。 可以发现，当催化剂孔径在1~500 nm范围内变化时，其对催化剂颗粒的有效因子影响非常显著。 当催化剂平均孔径从3 nm提升至10 nm时，有效因子从0.221提高至0.359。 当进一步提升平均孔径至100 nm时催化剂有效因子又提高1倍以上，达到0.743。可见大孔和介孔对克劳斯催化反应都是非常有利的，提高催化剂颗粒内的大孔和介孔数量是提高克劳斯工业催化剂性能最有效的途径。

图6 催化剂孔径对克劳斯催化剂有效因子的影响

2.6 催化剂几何构型的影响

催化剂的几何构型是影响催化剂颗粒外表面积和内扩散距离的重要因素。因此以6 mm直径的球形催化剂体积为基准构建了等体积的球形、 圆柱形、单孔圆柱、5孔圆柱体和9孔立方体5种不同结构和开孔率的克劳斯催化剂（如图1所示），并通过多物理场模拟对其进行了对比。 同时通过式(26)计算了不同构型催化剂特征尺寸Lp。

式中，Vp为催化剂颗粒体积，m3，Sp为催化剂颗粒的外表面积，m2。

图7以催化剂特征尺寸Lp为横坐标对比了相同反应条件下几种不同构型催化剂的有效因子。 结果表明，开孔催化剂具有更小的特征尺寸，克劳斯催化剂的有效因子随着催化剂开孔数的增加而增大。通过设计具有通孔结构的开孔催化剂，能够有效提高克劳斯催化剂的利用效率，同时又能避免因催化剂颗粒尺寸减小带来的床层压降增高的问题。

图7 催化剂几何构型对克劳斯催化剂有效因子的影响

3 结论

本文采用计算流体力学方法建立了克劳斯催化剂的三维稳态模型，通过多物理场耦合求解研究了反应温度、克劳斯反应本征速率、催化剂尺寸、孔隙率、孔径以及几何结构对克劳斯催化剂催化效率的影响，并由此直接积分计算得到了相应条件下催化剂颗粒的有效因子。

研究结果表明，减小催化剂颗粒直径，提高催化剂颗粒的介孔和大孔数量和直径，通过开孔减小催化剂颗粒的特征尺寸都是显著提高克劳斯催化剂颗粒有效因子的有效途径。 在克劳斯催化剂的本征活性测试中催化剂颗粒应破碎至0.2 mm以下才能有效地消除内扩散的影响。