复合材料板簧的迟滞特性建模与试验研究*
2021-07-05刘鹤龙史文库陈志勇孙云龙
刘鹤龙,史文库,高 蕊,陈志勇,陈 晃,孙云龙
(1.吉林大学,汽车仿真与控制国家重点实验室,长春 130022;2.中国重汽集团汽车研究总院,济南 250100;3.哈尔滨玻璃钢研究院有限公司,哈尔滨 150036)
前言
随着能源短缺的问题日益凸显和新能源汽车对续航里程的要求逐渐提高,汽车轻量化技术的发展得到了广泛的关注。纤维增强型复合材料(FRP)与金属材料相比,具有比强度高、比模量大、耐腐蚀性好等优点,因此在汽车轻量化领域上展现出了巨大的潜力。以复合材料板簧替代原钢板弹簧,不仅轻量效果明显,而且能够减轻汽车的非簧载质量,提高乘坐舒适性与行驶安全性。
近年来,国内外学者对复合材料板簧的研究主要集中在复合材料选择[1]、刚度预测[2-4]、连接结构设计[5]和疲劳性能优化[6]等方面,关于复合材料板簧的迟滞特性的研究却比较少见,而迟滞特性使板簧呈现非线性的刚度与阻尼,在整车的精细化建模中不可或缺。文献[7]中提出了一种复合材料板簧非线性迟滞特性模型,该模型可以比较准确地辨识台架试验的动态力-位移曲线,但模型参数与加载力幅值具有相关性,不利于在整车动力学分析上应用。对于传统的钢板弹簧,迟滞特性的建模方法主要包括有限元分析法[8]、Rate⁃dependent triboelastic(RT)模型[9]、Fancher模型[10]、Bouc⁃Wen模型[11]和Maxwell⁃slip模型[12]等。其中,Bouc⁃Wen模型由于计算简单、通用性好而被广泛应用于各种工程结构中。
然而,Bouc⁃Wen模型的未知参数数量较多,参数的物理意义尚不明确,因此,未知参数的辨识是该模型应用的一个难点。文献[13]和文献[14]中利用解析法对Bouc⁃Wen模型的参数辨识过程进行了详细的说明,但解析法计算过程相对复杂,通用性不佳。文献[11]和文献[15]中利用最小二乘法对Bouc⁃Wen模型的参数进行了辨识,但该方法容易被试验数据中的噪声干扰,具有一定的局限性。近年来,伴随着智能算法的兴起,遗传算法[16-17]、粒子群算法[18-19]、人工神经网络算法[20]和布谷鸟算法[21]等方法在非线性迟滞模型的参数辨识方法上展现出了极大的优势。
因此本文中尝试根据Bouc⁃Wen摩擦学理论建立复合材料板簧的迟滞特性模型,利用新兴的元启发算法(乌鸦搜索算法)对模型的未知参数进行辨识,并分析复合材料板簧的迟滞特性对整车动态响应的影响。
1 复合材料板簧力学台架试验
对某轻型客车后悬架复合材料板簧进行静/动态加载试验。板簧的结构形式为抛物线截面纵置单片簧,簧身为E玻纤/聚氨酯复合材料,纤维排布方向均为板簧圆周方向。复合材料簧身通过螺栓与端部金属接头连接。样件照片如图1所示。台架试验时,板簧中部用U型螺栓夹紧,用滚轮释放两端的自由度,台架试验装夹状态如图2所示。静态试验时,载荷由零缓慢逐级加载至目标值,再逐级卸载,静刚度测试结果如图3所示。通过对试验数据点的拟合可以得到复合材料板簧的线性静刚度为ks=118.15 N/mm。

图1 复合材料板簧样件

图2 复合材料板簧台架试验

图3 复合材料板簧静刚度测试结果
动态加载试验时,在一定的预载下(空载载荷),对样件施加不同频率、不同幅值力的正弦载荷。激励频率分别为0.5、1、1.5、2和2.5 Hz,每组频率下加载力幅值分别为700、1 400、2 100、2 800和3 500 N。
在加载力幅值为1 400 N的条件下,不同激励频率下复合材料板簧的等幅变频动态力-位移曲线如图4所示(去除了均值)。从图中可以看出,在试验频率范围内,加载频率对滞回曲线的影响不明显。与文献[22]中得出的在15 Hz以下、加载频率对钢板弹簧力-变形迟滞曲线影响不大的结论相符合。因此,为简化分析,本文中忽略加载频率对复合材料板簧滞回特性的影响。

图4 复合材料板簧等幅变频动态曲线
在加载频率为0.5 Hz的条件下,不同激励力幅值下复合材料板簧的等频变幅动态力-位移曲线如图5所示。从图中可以看出,随着加载幅值增大,滞回环的面积增加,表明阻尼大小与加载幅值呈正相关。
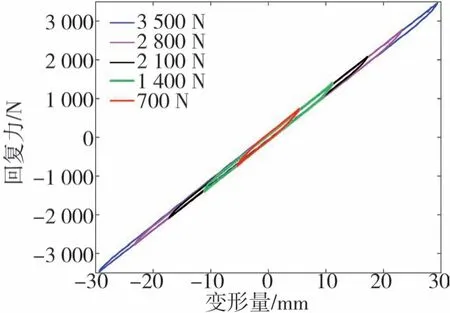
图5 复合材料板簧等频变幅动态曲线
2 复合材料板簧迟滞特性建模
2.1 复合材料板簧迟滞模型
传统的钢板弹簧迟滞特性主要由片间摩擦产生,金属材料本身的内阻可以忽略不计。而对于复合材料板簧,尤其是单片簧,通常认为簧身阻尼主要来源于复合材料基体的黏弹性和界面相的摩擦。吊耳处安装有橡胶衬套,也具有明显的摩擦非线性。因此,本文中尝试利用Bouc⁃Wen摩擦学理论建立复合材料板簧的迟滞特性模型。
Bouc⁃Wen模型的表达式为
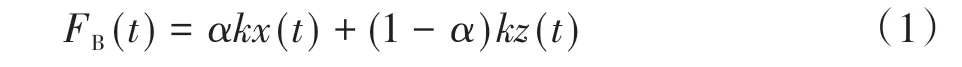
式中:FB(t)为板簧的非线性迟滞回复力,由线弹性恢复力和非线性迟滞力两部分组成;x(t)为板簧的响应位移量;z(t)为板簧的迟滞位移量;α、k为板簧的迟滞力参数。
其中,迟滞位移量z(t)的1阶微分形式为
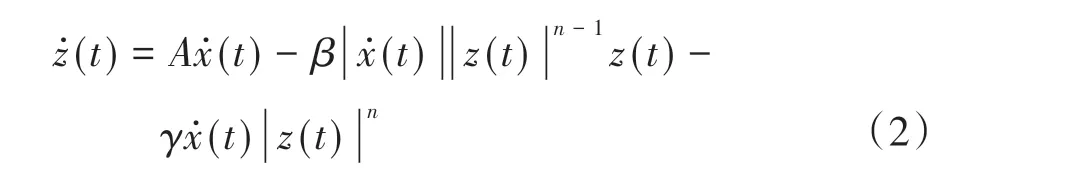
式中:A、β、γ为滞回环的形状参数;n为滞回环的光滑系数。
2.2 Bouc⁃Wen模型参数辨识
模型的参数辨识是非线性迟滞建模中最重要的环节之一,参数辨识的效果直接决定了建模的成败。复合材料板簧Bouc⁃Wen模型中待辨识参数较多,其中大部分参数的物理意义尚不明确,初值和范围难以确定,因此应用传统的最小二乘法、解析法等辨识方法具有一定的局限性。而近年来,新兴的元启发式优化算法借助大自然的智慧,通过模仿自然现象的运行机制,为解决复杂问题提供了新的思路与方法。
本文中尝试利用乌鸦搜索算法(crow search algorithm,CSA)对复合材料板簧的Bouc⁃Wen模型进行参数辨识,并对算法进行针对性的改进,以期提高算法的搜索精度与稳定性。
2.2.1 参数取值范围及适应度函数
Bouc⁃Wen模型中的未知参数包括k、A、α、β、γ、n共6个参数,α∈(0,1)。其中αk为板簧的线性刚度,理论上与静刚度结果接近[11]。根据静刚度测试结果(ks=118.15N/mm),取αk∈[100,140](N/mm)。参照文献[11]对钢板弹簧的模型参数辨识结果,并进行多次优化尝试[17],确定其他参数的优化范围为A、β、γ∈[0,10]。滞回环的形状参数n灵敏度较低,因此取n∈[0,4]。
适应度函数的质量决定了参数辨识的精度和效率,高质量的适应度函数应当能准确引导优化趋向,并节约计算时间。考虑模型对复合材料板簧多个试验幅值力下迟滞特性的通用性,定义综合相对回复力误差的均方根值(CRRMS)作为算法的适应度函数,即

式中:k为试验幅值力的数量,本文中k=5;Fampi对应每一组加载力的幅值;m为每组幅值力下试验数据点的个数;Ftest与Fsim分别为试验与仿真的回复力。
2.2.2 乌鸦搜索算法
乌鸦搜索算法(CSA)是伊朗学者Askarzadeh于2016年提出的新型群智能优化算法[23],CSA的进化过程模拟了乌鸦间相互跟踪窃食的行为,其有效性已在多个领域的优化问题上得到了证明[24-27]。算法的数学意义表示如下。

式(4)的位置迭代更新中存在两个问题:一是固定的飞行长度fl不能兼顾算法的全局搜索能力与局部搜索能力;二是当随机数大于AP时,乌鸦i以随机方式跟踪某一只乌鸦j进行位置更新,这种方式在迭代初期可以保持很好的种群多样性,有利于跳出局部最优,但也会使算法在迭代后期具有较大的盲目性,降低了算法的稳定性与搜索精度。
为解决以上问题,本文中提出一种改进的乌鸦搜索算法(modified crow search algorithm,MCSA),在标准乌鸦搜索的基础上,具体改动如下。
(1)基于segmoid函数,引入动态飞行长度:

式中:t为迭代次数;Maxgen为最大迭代次数。由式(5)得到的动态飞行长度随迭代次数变化曲线如图6所示。由图可见:在算法初期,飞行长度fl具有较大值,可以提高算法的全局搜索能力,避免陷入局部最优解;而在算法的后期,飞行长度fl具有较小值,可以提高算法的局部搜索能力,改善解的质量。

图6 动态飞行长度随迭代次数变化
(2)动态精英跟踪机制:
乌鸦i不再盲目选择任意乌鸦进行追踪,而是随机对精英乌鸦(适应度更好的个体)进行追踪。引入精英比例(pe)的概念,即适应度占比在前pe范围内的个体定义为精英乌鸦。随迭代次数变化的动态精英比例如式(6)所示。

在迭代初期,精英比例具有较大值,表明随机跟踪的乌鸦范围较广,有利于跳出局部最优;在迭代后期,精英比例具有较小值,表明随机跟踪的乌鸦范围较小,有利于局部搜索并提高算法的稳定性。
综上,MCSA的位置更新公式如下:
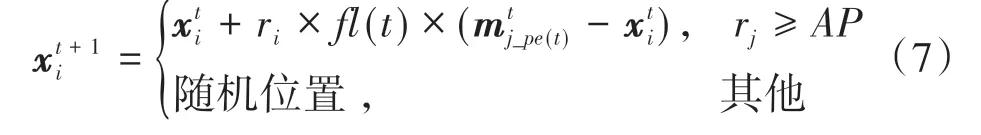
式中mj_pe(t)为根据式(6)计算得到的任意一只精英乌鸦j的食物记忆位置。
2.2.3 参数辨识结果与讨论
为验证改进的乌鸦搜索算法的有效性,将MCSA的优化性能与标准的乌鸦搜索算法(CSA)、标准遗传算法(GA)进行对比。种群数量为N=30,最大迭代次数Maxgen=200。取CSA与MCSA的意识概率AP=0.1,取CSA的飞行长度fl=2。GA的交叉概率为0.7,变异概率为0.1,采用轮盘赌选择。
每一种算法分别进行30次独立优化,分别提取每种算法30次优化结果的最差值(Worst)、最优值(Best)、均值(Mean)和标准差值(Std.),如表1所示。3种算法的平均迭代寻优对比曲线如图7所示。通过表1和图7的3种算法寻优结果对比发现,MCSA的各项指标均优于GA和CSA,表明MCSA算法在保证更高求解精度的同时,具有更好的稳定性。

表1 算法求解结果对比
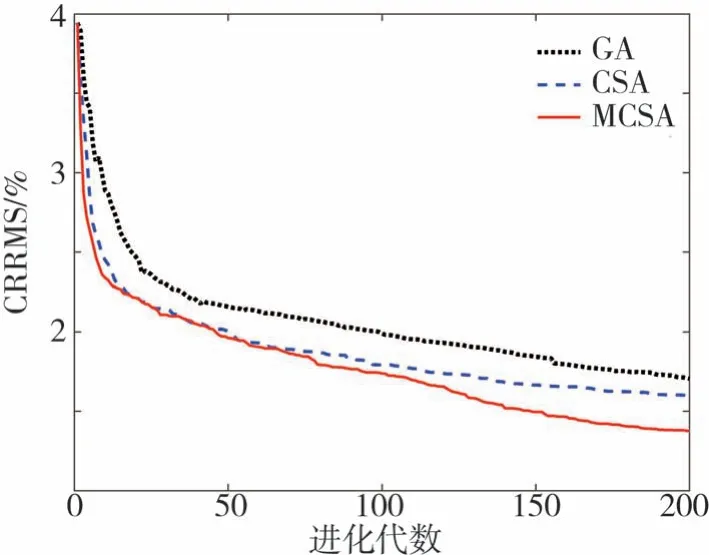
图7 算法的平均迭代寻优曲线
复合材料板簧Bouc⁃Wen迟滞模型参数辨识的最优结果如表2所示。根据表2参数结果计算得到的复合材料板簧动态力-位移曲线与试验对比如图8~图12所示。从图中可以看出,在每个加载幅值力的条件下,复合材料板簧的动态仿真曲线与试验曲线均吻合良好,表明前面利用MCSA辨识的模型参数是准确的,也说明Bouc⁃Wen模型对复合材料板簧的迟滞特性建模具有较好的适用性。

表2 Bouc⁃Wen模型辨识最优结果

图8 幅值700 N动态曲线仿真与试验对比
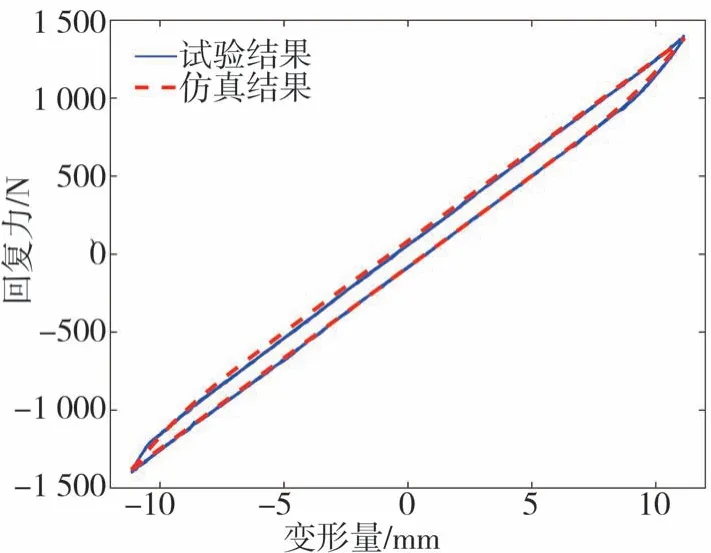
图9 幅值1 400 N动态曲线仿真与试验对比

图10 幅值2 100 N动态曲线仿真与试验对比
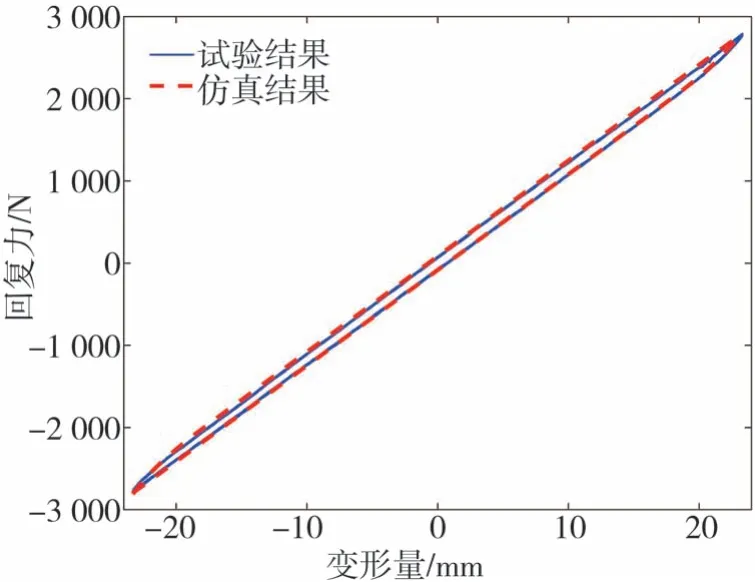
图11 幅值2 800 N动态曲线仿真与试验对比
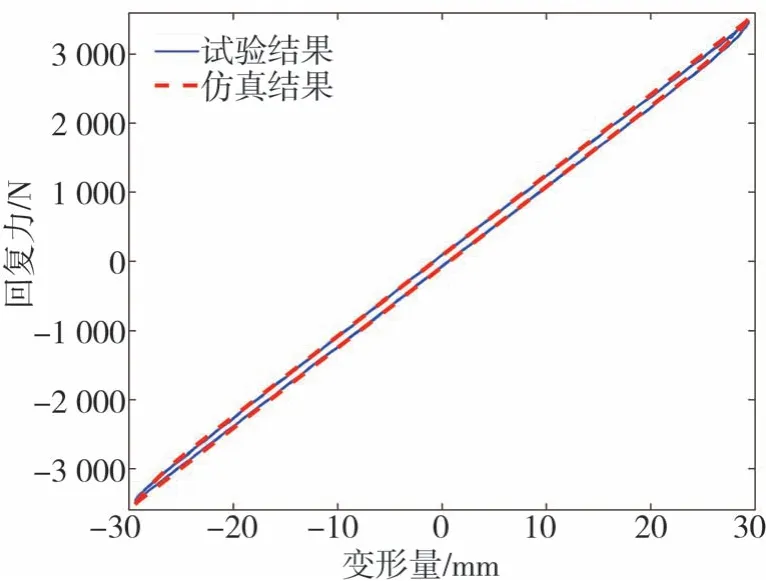
图12 幅值3 500 N动态曲线仿真与试验对比
3 整车平顺性建模
3.1 考虑板簧迟滞特性的整车模型
某轻型客车前悬架为双横臂扭簧结构,后悬架为板簧结构。以前面辨识的Bouc⁃Wen迟滞模型单元替代后悬架的弹性单元,建立考虑复合材料板簧迟滞特性的整车模型,如图13所示。

图13 整车平顺性模型
在针对悬架特性的低频平顺性研究中(一般低于15 Hz),所研究的路面输入的最短波长远大于轮胎与地面的接触印迹,因而可以将滚动轮胎的垂向动力学特性简化为一个忽略了阻尼的弹簧[28]。因此,本文的整车模型忽略了轮胎的阻尼对动力学的影响[11,29]。该模型为整车7自由度模型,包括簧载部分的垂向运动zb、俯仰运动θb、侧倾运动φb3个自由度和4个车轮的垂向自由度zwi。qi为路面激励,FBW为板簧的回复力,i=A,B,C,D代表4个车轮。
在俯仰角θb和侧倾角φb较小时,4个车轮对应车身上方的垂向位移自由度:
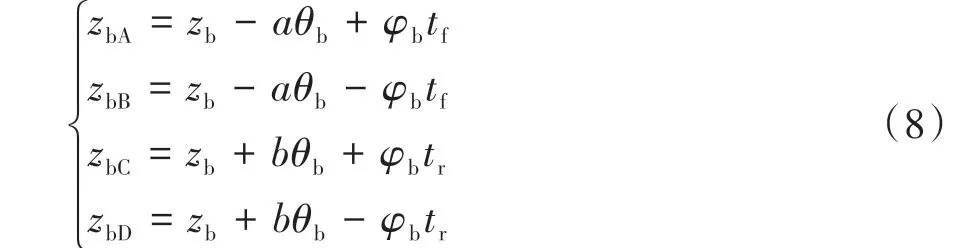
根据牛顿运动定律,列出整车模型的运动方程:
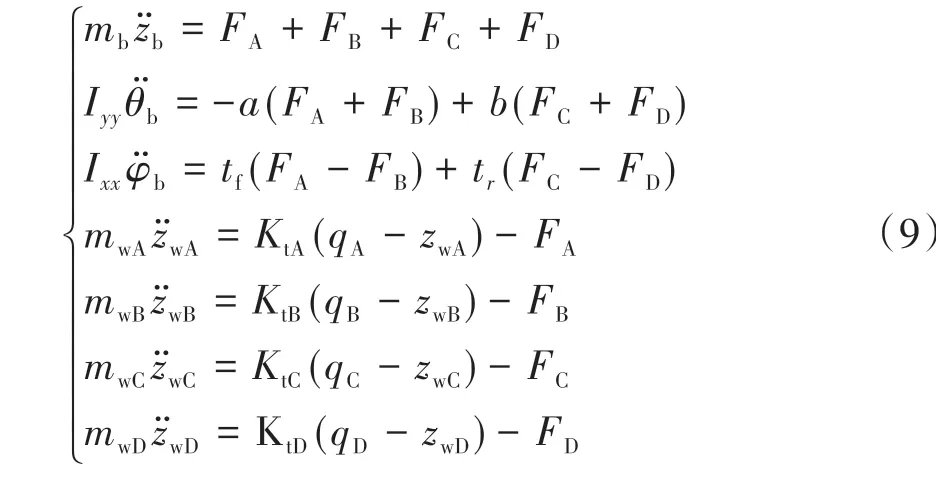
式中FA、FB、FC和FD为悬架回复力:

考虑方程组的复杂性,本文中基于Simulink平台,根据式(8)~式(10)搭建动力学模型,选用求解器ode45(4阶-5阶Runge-Kutta)实现对动力学方程的求解。表3给出了某轻型客车的整车动力学相关参数。
3.2 整车模型准确性验证
为验证整车7自由度模型的正确性,对某轻型客车进行后轮跌落试验。复合材料板簧装车状态如图14所示。

图14 复合材料板簧装车状态
后轮跌落试验如图15所示。将两个后轮置于相同高度的凸台上(9 cm),缓慢推动客车,使两后轮同时跌落,用加速度传感器分别采集后轮上方车架处(图14)和驾驶员脚部的振动衰减信号(图16)。仿真与试验结果对比如图17和图18所示,仿真与试验的振动加速度信号吻合较好,验证了整车7自由度模型的准确性。

图15 后轮跌落试验

图16 驾驶员脚部传感器布置图

图17 后车架振动加速度信号对比图

图18 驾驶员脚部振动加速度信号对比图
4 迟滞特性对整车动态响应的影响
采用滤波白噪声法[30]生成四轮汽车B级路面随机激励时域模型作为输入,仿真的车辆行驶速度为60 km/h。为体现复合材料板簧迟滞特性的影响,分别对考虑板簧迟滞特性的非线性Bou⁃Wen模型(BM)与不考虑迟滞特性的线性化模型(LM)进行整车动态响应分析。簧载质量质心加速度ab、悬架动挠度SDD和复合材料板簧回复力FLS3个参数对比如图19~图21所示,其均方根值和相对误差如表4所示。
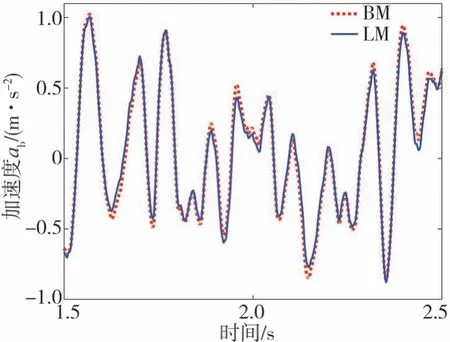
图19 簧载质量质心加速度对比图

表4 复合材料板簧迟滞特性对整车动态响应的影响
图19为簧载质量质心加速度对比曲线,表明在分析工况下,该复合材料板簧的迟滞特性使质心加速度的均方根值增加了5.09%,对行驶平顺性有一定不利影响;图20为悬架动挠度对比曲线,表明该复合材料板簧的迟滞特性使悬架动挠度减小了6.58%,有利于行驶安全性;图21为板簧回复力对比曲线,表明该复合材料板簧的迟滞特性使回复力增加了3.49%,这是由于复合材料板簧的迟滞特性考虑了板簧的非线性刚度和阻尼效应,致使悬架动挠度明显偏小、复合材料板簧所提供的垂向力偏大。
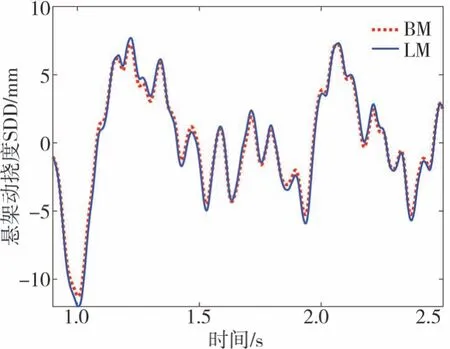
图20 悬架动挠度对比图
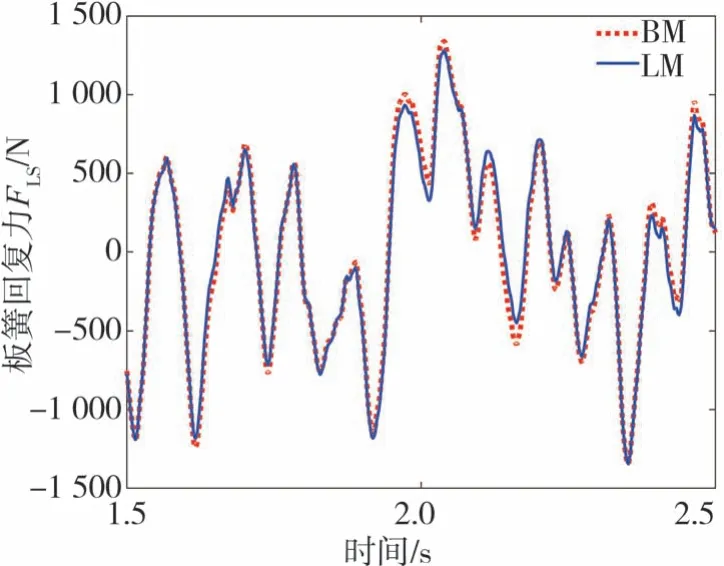
图21 板簧回复力对比图
5 结论
(1)本文中利用Bouc⁃Wen模型对复合材料纵置单片簧的迟滞特性进行建模,仿真的动态力-位移曲线与试验结果吻合良好,表明Bouc⁃Wen模型对复合材料板簧的迟滞特性具有较好的适用性。
(2)改进的乌鸦搜索算法对Bouc⁃Wen非线性迟滞模型的参数辨识具有较高的精度和稳定性,体现了新兴的群智能算法在非线性迟滞模型参数辨识上的有效性。
(3)通过建立整车7自由度模型分析复合材料板簧迟滞特性对动态响应的影响,结果表明复合材料板簧的迟滞特性使簧载质量的质心加速度增加,板簧的回复力增大,而悬架的动挠度减小。
